Preview text:
Phßng gi¸o dôc & ®µo t¹o ®Ò thi CHỌN häc sinh giái líp 7 thcs cÊp huyÖn HuyÖn HOẰNG HÓA n¨m häc: 2016 - 2017 M«n thi: To¸n §Ò chÝnh thøc
Thêi gian lµm bµi: 120 phót (§Ò thi gåm cã 01 trang) Ngµy thi: 21/ 02/ 2017 C©u 1( 4 ®iÓm): 12 5 6 2 10 3 2 2 2 .3 4 .9 5 .7 25 .49
a) Thực hiện phép tính: A 2 .36 8 .3 125.73 9 3 2 4 5 5 .14 1 1 1 1 1 1 1 b) Chøng minh r»ng : ... ... 2 4 4n2 4n 98 100 7 7 7 7 7 7 50
c) TÝnh: B = 12+ 22 + 32 + 42 + 52 +……….+ 982
d) Cho p lµ sè nguyªn tè lín h¬n 3 chøng minh r»ng: p2 - 1 chia hÕt cho 24 1 4 2
C©u 2( 3 ®iÓm):a) Tìm x biết x 3 ,2 3 5 5 3 2
b) Cho C = m 3m 2m 5 với m N Chứng minh C là số hữu tỉ m(m 1)(m 2) 6
c) Cho M = (x - 1)(x + 2)(3 - x). Tìm x để M < 0 2 2 a c a C©u 3 (4 ®iÓm): a) Cho a c chứng minh rằng: c b 2 2 b c b
b) Tìm các giá trị nguyên của x và y biết: x2 – y2 = 5 C©u 4 (6 ®iÓm): Cho tam gi¸c ABC cã 0 BAC 75 , 0
ABC 35 . Ph©n gi¸c cña gãc BAC c¾t c¹nh
BC t¹i D . §êng th¼ng qua A vµ vu«ng gãc víi AD c¾t tia BC t¹i E . Gäi M lµ
trung ®iÓm cña DE . Chøng minh r»ng:
a) Tam gi¸c ACM lµ tam gi¸c c©n. AD AE b) AB . 2
c) Chu vi tam gi¸c ABC b»ng ®é dµi ®o¹n th¼ng BE . C©u 5 (2 ®iÓm):
a). T×m mét sè cã ba ch÷ sè, biÕt r»ng sè ®ã chia hÕt cho 18 vµ c¸c ch÷ sè cña nã tØ lÖ víi ba sè 1, 2 vµ 3.
b).Cho f(x)= 3x2 - 2x -1 Tìm x để f(x) = 0
---------------------------HÕt----------------------------- Híng dÉn chÊm C©u ý Tãm t¾t lêi gi¶i §iÓm C©u1 a. 12 5 6 2 10 3 2 2 12 5 12 4 10 3 4 4 2 .3 4.9 5 .7 25.49 2 .3 2 .3 5 .7 5.7 4® (2®) A 2. 6 3 8 .3 125. 3 12 6 12 5 9 3 9 3 3 9 3 2 4 5
7 5.14 2 .3 2 .3 5.7 5.2.7 0.5 2 .3 .3 4 3 1 5.7 6 . 5 4 3 7 5.7 2 .3.2 6 12 4 12 4 . 5 6 7 1 5 7 12 5 2 .3 .3 9 3 1 5.7 3 . 12 12 5 9 3 5 2 .3.4 5.7.9 6 5.9 5 5. 6 0.5 3 2(5 7) 2429 5 2.5.9 6250 b. 1 1 1 1 1 1 0.5 (2®) §Æt A= ... ... 2 4 4n2 4n 98 100 7 7 7 7 7 7 1 1 1 1 1 Ta cã: 49A=1 ... ... 0.5 2 4n4 4n2 96 98 7 7 7 7 7 1 1 50A 1 1 A (®pcm) 100 7 50 C
: B = 12+ 22 + 32 + 42 + 52 +……….+ 982 = (1.2+2.3+3.4+....98.99) 1,0
– (1+2+3+4+.....97+98) = 318549 d P2-1=(p-1)(p+1) 1,0
Vì p >3 nên p lẻ => (p-1)(p+1) là tích hai số chẵn nên chia hết cho 8 * .
Ta có (p-1)p(p+1)là tích 3 số nguyên liên tiếp nên có 1 số chia hết
cho 3 mà p là số nguyên tố lớn hơn 3 nên p không chia hết cho 3
vậy trong hai số (p-1);(p+1) phải có 1 số chia hết cho 3 (**)
Vì (8;3) = 1 => P2-1 chia hết cho 24 C©u2 a. 1 4 x 3 , 2 2 1 4 1 6 2 4® (1®) x 3 5 5 3 5 5 5 0.5 1 4 1 4 x 3 5 5 0.5 1 7 x 2 1 x 3 3 x 2 1 5 3 x 2 x 3 3 1.0 b)
Sö dông PP chøng minh P/S tèi gi¶n c¶ tö vµ mÉu cã ¦CLN b»ng c Có 2 T/H xảy ra 1,0 C©u3 a) Từ a c suy ra 2 1.0 c . a b 4® 1.5® c b 2 2 2 a c a . a b a(a b) a khi đó = 2 2 2 b c b . a b b(a b) b b)
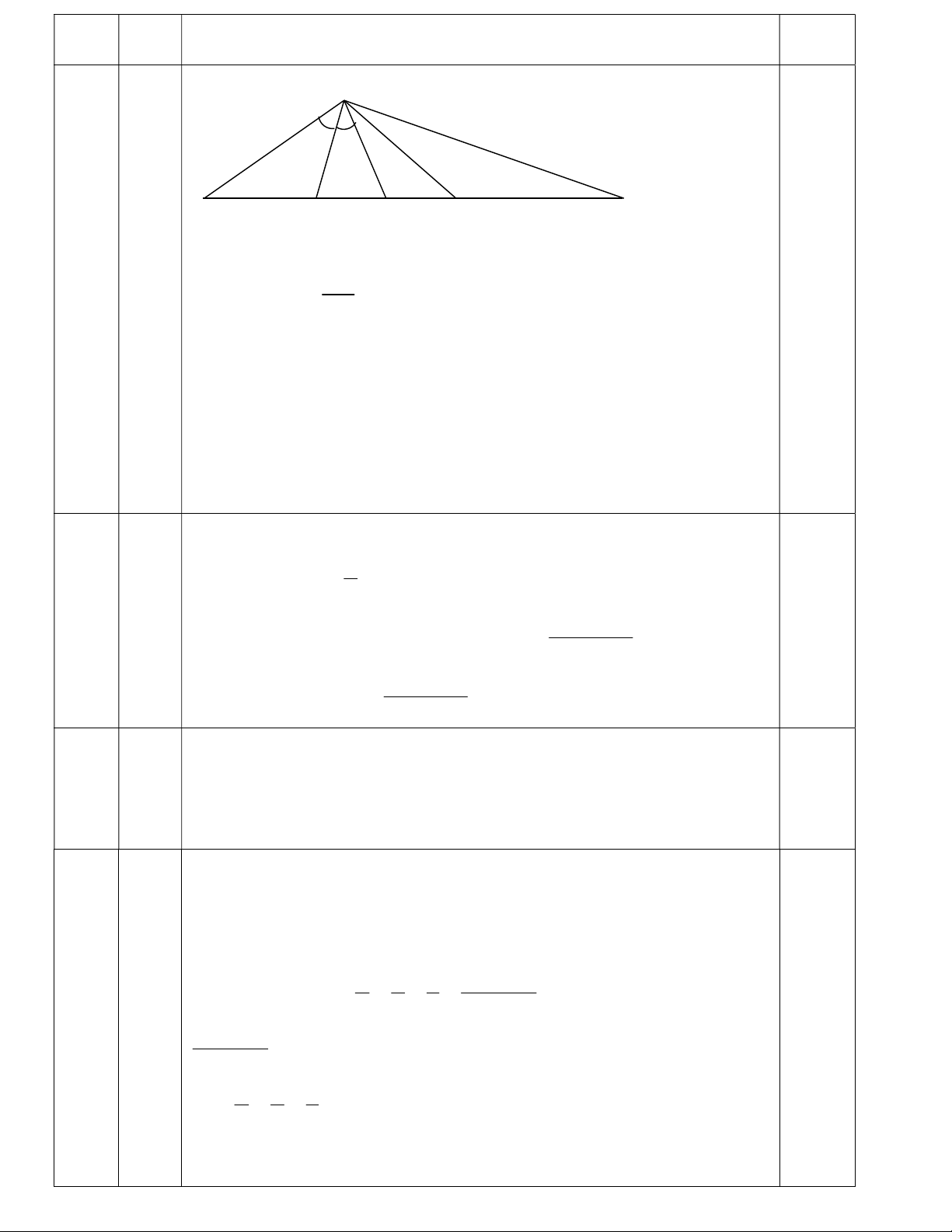
Tách : x2 – y2 = (x+y)(x-y) =5 tìm giá trị nguyên 1 C©u4 a) A 6® 2.0® 350 B D C M E Ta cã: BAD 0 75 0 CAD 37 30' ADM ABD 0 BAD 72 30' 2 0.5
( Gãc ngoµi cña tam gi¸c ABD );
Tam gi¸c DAE vu«ng cã AM lµ trung tuyÕn nªn MAD c©n t¹i M , do ®ã 0 AMD 0 0 0 180
2.ADM 180 145 35 (1) 0.5
Trong tam gi¸c ABC ta l¹i cã: 0 BAC 0 ABC 0 75 , 35 ACB 70 0.5 0.5 CAM ACB 0 AMC 35 (2)
Tõ (1) vµ (2) suy rat tam gi¸c ACM c©n b) Theo ý a, ta cã: ABM 0 AMB 35 AB AM (3) 0.5 2.0® 1
MÆt kh¸c: AM DE (Trung tuyÕn thuéc c¹nh huyÒn cña tam 0.5 2 AD AE 0.5
gi¸c vu«ng) mµ DE AD AE AM (4) 2 AD AE Tõ (3) vµ (4) AB (®pcm) 0.5 2 c)
Ta cã: AC CM ( ACM c©n), MA ME( A ME c©n) 1.0 2.0 ® AM AB( A BM c©n). 0.5
Do ®ã: BE BC CA AB 0.5 C©u5
Gäi ba ch÷ sè ph¶i t×m lµ a, ,
b c ; sè ®ã chia hÕt cho 18 nªn chia 2®
hÕt cho 9 a b c9 .
L¹i cã: 1 a b c 27
Suy ra: a b c nhËn mét trong ba gi¸ trÞ 9, 18, 27 (3) 0.5 a b c a b c
Theo bµi ra, ta cã: mµ a N nªn 1 2 3 6 a b c
N (4). Tõ (3) vµ (4) a b c 18 6 0.5 a b c
VËy 3. Tõ ®ã ta cã a 3,b 6,c 9 . 1 2 3 0.5
Do sè cÇn t×m chia hÕt cho 18 nªn ch÷ sè hµng ®¬n vÞ ph¶i lµ sè
ch½n. VËy sè cÇn t×m lµ: 396 hoÆc 936 0.5




