Đề thi HSG Toán 8 cấp huyện năm 2016 – 2017 phòng GD&ĐT Hậu Lộc – Thanh Hóa

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề thi HSG Toán 8 cấp huyện năm 2016 – 2017 phòng GD&ĐT Hậu Lộc – Thanh Hóa; đề thi có đáp án, lời giải chi tiết và thang chấm điểm.

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 8

Môn: Toán 8

Thông tin:

5 trang 4 tháng trước

Tác giả:

Profile Mai Nguyệt
PHÒNG GD&ĐT HUYỆN
HẬU LỘC
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN
NĂM HỌC 2016-2017
Môn: Toán - Lớp 8
Th
ời gian l
àm bài: 15
0 phút
(Không kể thời gian giao đề)
Câu 1: (4 điểm) Cho biểu thức: A =
2
2 9 3 2 4
5 6 2 3
x x x
x x x x
a) Rút gọn biểu thức A.
b) Tìm x để A nhận giá trị là một số nguyên.
Câu 2: (4 điểm)
a) Giải phương trình:
2 2
5 1 4 1
2
2 1 1
x x x x
x x
b) Giải phương trình: x
6
– 7x
3
– 8 = 0
Câu 3:( 3 điểm)
a) Phân tích đa thức sau thành nhân tử : x
20
+ x
+1
b) Tìm số nguyên x thỏa mãn cả hai bất phương trình:
3 2
0,8
5 2
x x
và
2 5 3
1
6 4
x x
Câu 4. (3 điểm)
a) Tìm các cặp số nguyên (x, y) thỏa mãn:
2
2 3 2 0
y xy x
b) Cho x, y thoả mãn
1
xy
. Chứng minh rằng:
2 2
1 1 2
1 1 1
x y x y
Câu 5: (6 điểm)
Cho tam giác ABC có ba góc nhọn, các đường cao BD, CE cắt nhau tại H.
a) Chứng minh ABD ACE.
b) Chứng minh BH.HD = CH.HE.
c) Nối D với E, cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng DE theo
a.
--------------------------------------Hết--------------------------------------------
SBD…………………………….Họ tên thí sinh:…………………………….
Chữ ký giám thị:……………………………………………………………..
HD CHẤM ĐỀ THI CHỌN HSG CẤP HUYỆN NĂM HỌC 2016-2017
MÔN TOÁN 8: Thời gian 150 phút
Câu Nội dung Điểm
Câu 1
(4.0 điểm)
Cho biểu thức: A =
2
2 9 3 2 4
5 6 2 3
x x x
x x x x
a) ĐKXĐ: x
2 , x
3.
2 9 3 2 4
( 3)( 2) 2 3
x x x
A
x x x x
2
2 8
( 3)( 2)
x x
x x
=
( 4)( 2)
( 3)( 2)
x x
x x
=
4
3
x
x
b/ Ta có: A =
4 7
1
3 3
x
x x
§Ó A
Z th× x - 3
¦(7) =
7; 1; 1; 7
=> x
4; 2; 4; 10
KÕt hîp víi §KX§ ta ®îc x
4; 4; 10
0,5
0,5
1,0
0,5
0,25
0,25
0,5
0,5
Câu 2
(4.0 điểm)
a/
2 2
5 1 4 1
2
2 1 1
x x x x
x x
ĐKXĐ:
2
1
;1 xx
01
1
2
15
1
1
14
22
x
xx
x
xx
0
1
2
23
1
23
22
x
xx
x
xx
2
1 1
3 2 0
1 2 1
x x
x x
2
3 2 3 2 0
1 2 3 2 0 (1)
x x x
x x x
Giải phương trình (1) x =1 ; x = 2 ; x = - 2/ 3 (thỏa mãn
ĐKXĐ)
Vậy phương trình đã cho có tập nghiệm là S =
3
2
;2;1
.
0,25
0,25
0,25
0,25
0,25
0,5
0,25
b) Ta có x
6
– 7x
3
– 8 = 0
(x
3
+ 1)(x
3
– 8) = 0
(x + 1)(x
2
– x + 1)(x – 2)(x
2
+ 2x + 4) = 0 (*)
Do x
2
– x + 1 = (x –
1
2
)
2
+
3
4
> 0
và x
2
+ 2x
+ 4 = (x + 1)
2
+ 3 > 0 với mọi x
nên (*)
(x + 1)(x – 2) = 0
1
2
x
x
Vậy phương trình đã cho có tập nghiệm là S = {- 1; 2}
0,25
0,25
0,25
0,25
0,5
0,25
0,25
Câu 3
(3.0 điểm)
a) x
20
+ x
+1 = x
20
-x
2
+x
2
+x+1
= x
2
(x
18
-1) +(x2+x+1)
=x
2
(x
9
+1)(x
9
-1)+(x
2
+x+1)
=x
2
(x
9
+1)(x
3
-1)(x
6
+x
3
+1)+(x
2
+x+1)
=x
2
(x
9
+1)(x-1)(x
2
+x+1)(x
6
+x
3
+1)+(x
2
+x+1)
=(x
2
+x+1)[x
2
(x
9
+1)(x-1)(x
6
+x
3
+1)+1]
b) Giải bất phương trình (1):
3 2
0,8
5 2
x x
3 2 8
5 2 10
x x
4 8
10 10
x
12 0 12
x x
Giải bất phương trình (2):
2 5 3
1
6 4
x x
3 2 5
1
4 6
x x
1 13
1 0
12 12
x x
13
x
Vì x là nghiệm chung của hai bất phương trình (1) và (2)
nên ta có x = 12
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
Câu 4
( 3,0 điểm)
a) Ta có:
2 2 2 2
2 3 2 0 2 3 2
y xy x x xy y x x
(*)
2
( ) ( 1)( 2)
x y x x
VT của (*) là số chính phương; VP của (*) là tích của 2
số nguyên liên tiếp nên phải có 1 số bằng 0
1 0 1 1
2 0 2 2
x x y
x x y
Vậy có 2 cặp số nguyên
( ; ) ( 1;1)
x y
hoặc
( ; ) ( 2; 2)
x y
0,25
0,25
0,25
0,
2
5
b)
2 2
1 1 2
1 1 1x y xy
(1)
2 2
2 2
2
2 2
1 1 1 1
0
1 1 1 1
0
1 1 1 1
1
0 2
1 1 1
x xy y xy
x y x y x y
x xy y xy
y x xy
x y xy
Vì
1; 1
x y
1
xy
1 0xy
BĐT (2) luôn đúng BĐT (1) luôn đúng
(D
ấu ‘’=’’ xảy ra khi x = y)
0,5
0,25
0,5
0,25
0,5
Câu 5
( 6,0 điểm)
a)
Xét ABD và ACE có:
Góc A chung
0
90ADB AEC
ABD ACE. (g-g)
b) Xét BHE và CHD có :
0
90BEH CDH
BHE CHD ( đối đỉnh)
BHE CHD (g-g)
BH HE
CH HD
Suy ra BH.HD = CH.HE.
2,0
1,0
1,0
A
B
C
D
E
H
c)
Khi AB = AC = b thì ABC cân tại A
Suy ra được DE // BC
DE AD
BC AC
DE =
.AD BC
AC
Gọi giao điểm của AH và BC là F AF BC, FB = FC
=
2
a
DBC FAC
DC BC
FC AC
.BC FC
DC
AC
=
2
2
a
b
DE =
.AD BC
AC
=
( ).AC DC BC
AC
=
2
( ).
2
a
b a
b
b
=
2 2
2
(2 )
2
a b a
b
0,25đ
0,25đ
0,25đ
0,5đ
0,25đ
0,5đ
Lưu ý: - Bài hình học sinh không vẽ hình hoặc vẽ hình sai không chấm điểm.
- Học sinh làm cách khác đúng vẫn cho điểm tối đa.
A
B
C
D
E
H
F
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GD&ĐT HUYỆN
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN HẬU LỘC NĂM HỌC 2016-2017 Môn: Toán - Lớp 8
Thời gian làm bài: 150 phút (Không kể thời gian giao đề)
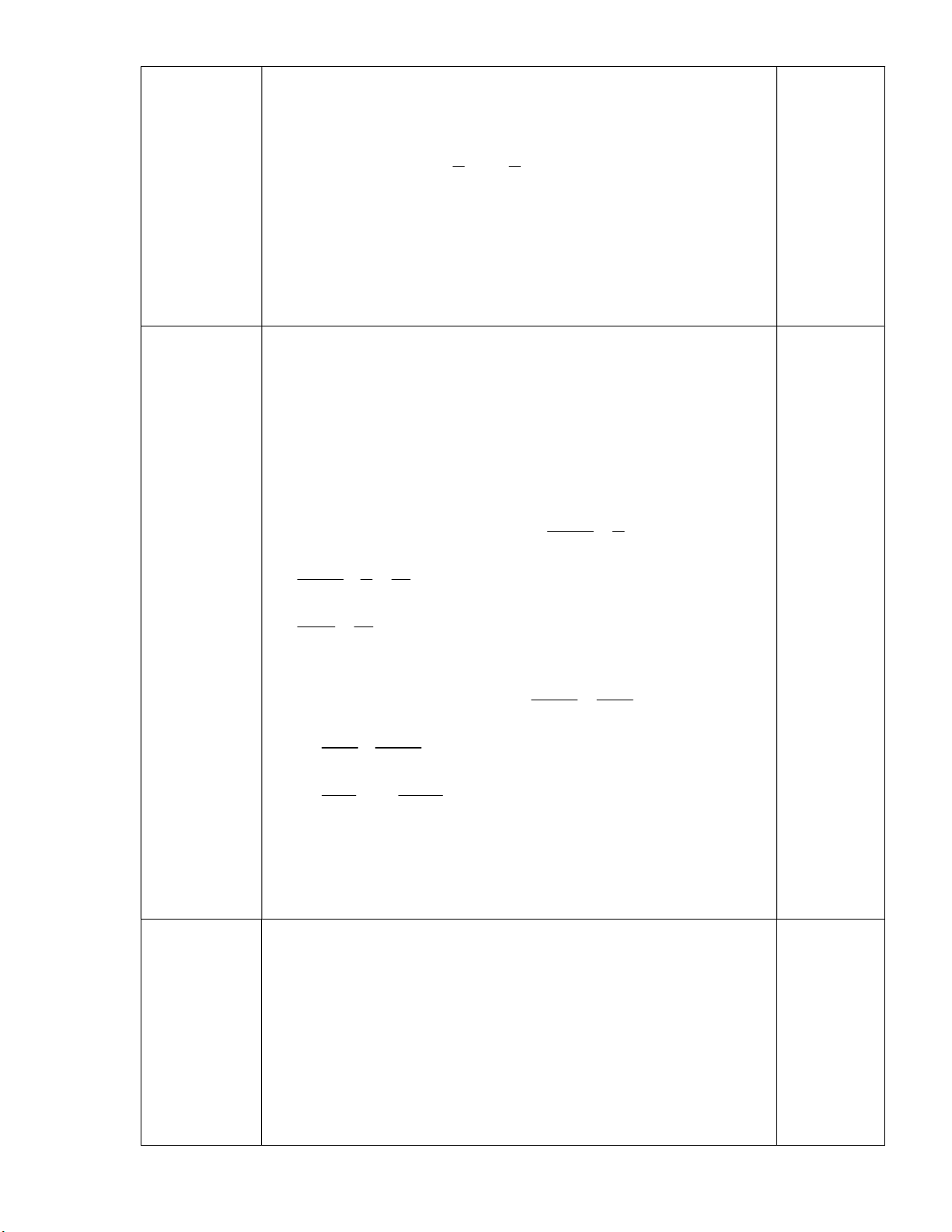
Câu 1: (4 điểm) Cho biểu thức: A = 2x  9 x  3 2x  4   2 x  5x  6 x  2 3  x
a) Rút gọn biểu thức A.
b) Tìm x để A nhận giá trị là một số nguyên. Câu 2: (4 điểm) 2 2
a) Giải phương trình: x  5x 1 x  4x 1  2   2x 1 x 1
b) Giải phương trình: x6 – 7x3 – 8 = 0 Câu 3:( 3 điểm)
a) Phân tích đa thức sau thành nhân tử : x20 + x +1
b) Tìm số nguyên x thỏa mãn cả hai bất phương trình: 3x  2 x     x x 0,8 và 2 5 3 1  5 2 6 4 Câu 4. (3 điểm)
a) Tìm các cặp số nguyên (x, y) thỏa mãn: 2 y  2xy  3x  2  0
b) Cho x, y thoả mãn xy  1. Chứng minh rằng: 1 1 2   2 2 1  x 1  y 1  x y Câu 5: (6 điểm)
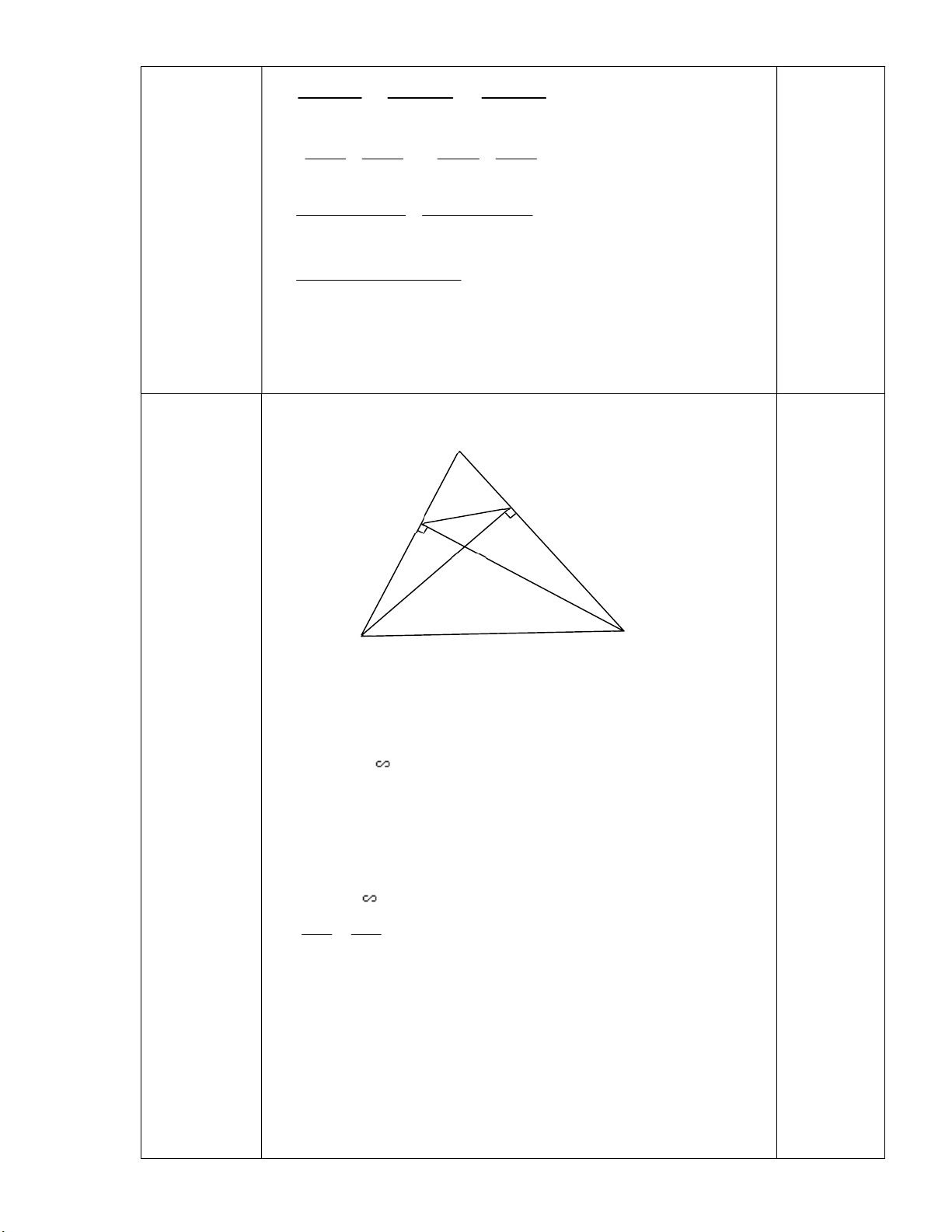
Cho tam giác ABC có ba góc nhọn, các đường cao BD, CE cắt nhau tại H.
a) Chứng minh ABD ACE.
b) Chứng minh BH.HD = CH.HE.
c) Nối D với E, cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng DE theo a.
--------------------------------------Hết--------------------------------------------
SBD…………………………….Họ tên thí sinh:…………………………….
Chữ ký giám thị:……………………………………………………………..
HD CHẤM ĐỀ THI CHỌN HSG CẤP HUYỆN NĂM HỌC 2016-2017
MÔN TOÁN 8: Thời gian 150 phút Câu Nội dung Điểm
Cho biểu thức: A = 2x  9 x  3 2x  4   2 x  5x  6 x  2 3  x a) ĐKXĐ: x  2 , x  3. 0,5 Câu 1 2x  9 x  3 2x  4 A    (4.0 điểm) (x  3)(x  2) x  2 x  3 0,5 2 x  2x  8    = (x 4)(x 2) (x  3)(x  2) (x  3)(x  2) 1,0 = x  4 x  3 0,5 b/ Ta có: A = x  4 7  1 x  3 x  3 0,25
§Ó A  Z th× x - 3 ¦(7) =  7  ; 1  ; 1;  7 0,25 => x   4  ; 2; 4; 1  0 0,5
KÕt hîp víi §KX§ ta ®­îc x   4  ; 4; 1  0 0,5 2 2 a/ x  5x 1 x  4x 1    2 2x 1 x 1 ĐKXĐ: 1 0,25 x   ; 1 x   2 2 2 x  4x  1 x  5x  1   0,25 1 1  0 x  1 2x 1 Câu 2 2 2 0,25 x  3x  2 x  3x  2    (4.0 điểm) 0 x 1 2x  1  0,25 2    x  x   1 1 3 2   0    x 1 2x 1   2
x  3x  23x  2  0  x  
1 x  23x  2  0 (1) 0,25
Giải phương trình (1) x =1 ; x = 2 ; x = - 2/ 3 (thỏa mãn 0,5 ĐKXĐ)
Vậy phương trình đã cho có tập nghiệm là S =  2  ; 1 ; 2   . 0,25  3
b) Ta có x6 – 7x3 – 8 = 0 0,25  (x3 + 1)(x3 – 8) = 0 0,25
 (x + 1)(x2 – x + 1)(x – 2)(x2 + 2x + 4) = 0 (*) 0,25
Do x2 – x + 1 = (x – 1 )2 + 3 > 0 2 4 0,25
và x2 + 2x + 4 = (x + 1)2 + 3 > 0 với mọi x 0,5
nên (*)  (x + 1)(x – 2) = 0 x  1   0,25  x  2 0,25
Vậy phương trình đã cho có tập nghiệm là S = {- 1; 2} Câu 3 a) x20 + x +1 = x20-x2+x2+x+1 (3.0 điểm) = x2(x18-1) +(x2+x+1) 0,25 =x2(x9+1)(x9-1)+(x2+x+1) 0,25 0,25
=x2(x9+1)(x3-1)(x6+x3+1)+(x2+x+1) 0,25
=x2(x9+1)(x-1)(x2+x+1)(x6+x3+1)+(x2+x+1) 0,25
=(x2+x+1)[x2(x9+1)(x-1)(x6+x3+1)+1] 0,25
b) Giải bất phương trình (1): 3x  2 x   0,8 5 2 3x  2 x 8    5 2 10 x  4 8   0,25 10 10
 x 12  0  x  12 0,25
Giải bất phương trình (2): 2x  5 3  x 1  6 4 3  x 2x  5  1   4 6 x 1 x 13  1    0 0,25 12 12  x 13 0,25
Vì x là nghiệm chung của hai bất phương trình (1) và (2) nên ta có x = 12 0,5 Câu 4 a) Ta có: ( 3,0 điểm) 2 2 2 2
y  2xy  3x  2  0  x  2xy  y  x  3x  2 0,25 (*) 2
 (x  y)  (x 1)(x  2) 0,25
VT của (*) là số chính phương; VP của (*) là tích của 2
số nguyên liên tiếp nên phải có 1 số bằng 0 x 1  0 x  1  y  1    0,25 x 2 0    x  2  y  2
Vậy có 2 cặp số nguyên (x; y)  (1;1) hoặc (x; y)  (2;2) 0,25 1 1 2 b)   2 2 1  x 1  y 1  xy (1)  1 1   1 1       0  0,5 2   2  1 x 1 xy  1 y 1 xy  x  y  x y x  y     0 2 1 x 1 xy  2 1 y 1 xy 0,25  y  x2  xy   1    0 2 0,5 2 1 x  2 1 y    1 xy
Vì x  1; y  1  xy  1  xy 1  0 0,25
 BĐT (2) luôn đúng  BĐT (1) luôn đúng
(Dấu ‘’=’’ xảy ra khi x = y) 0,5 Câu 5 a) ( 6,0 điểm) A D E H B C Xét ABD và ACE có: Góc A chung  ADB   0 AEC  90  ABD ACE. (g-g) 2,0
b) Xét BHE và CHD có :  BEH   0 CDH  90  BHE   CHD ( đối đỉnh) 1,0  BHE CHD (g-g)  BH HE  CH HD 1,0 Suy ra BH.HD = CH.HE. c) A E D H B F C
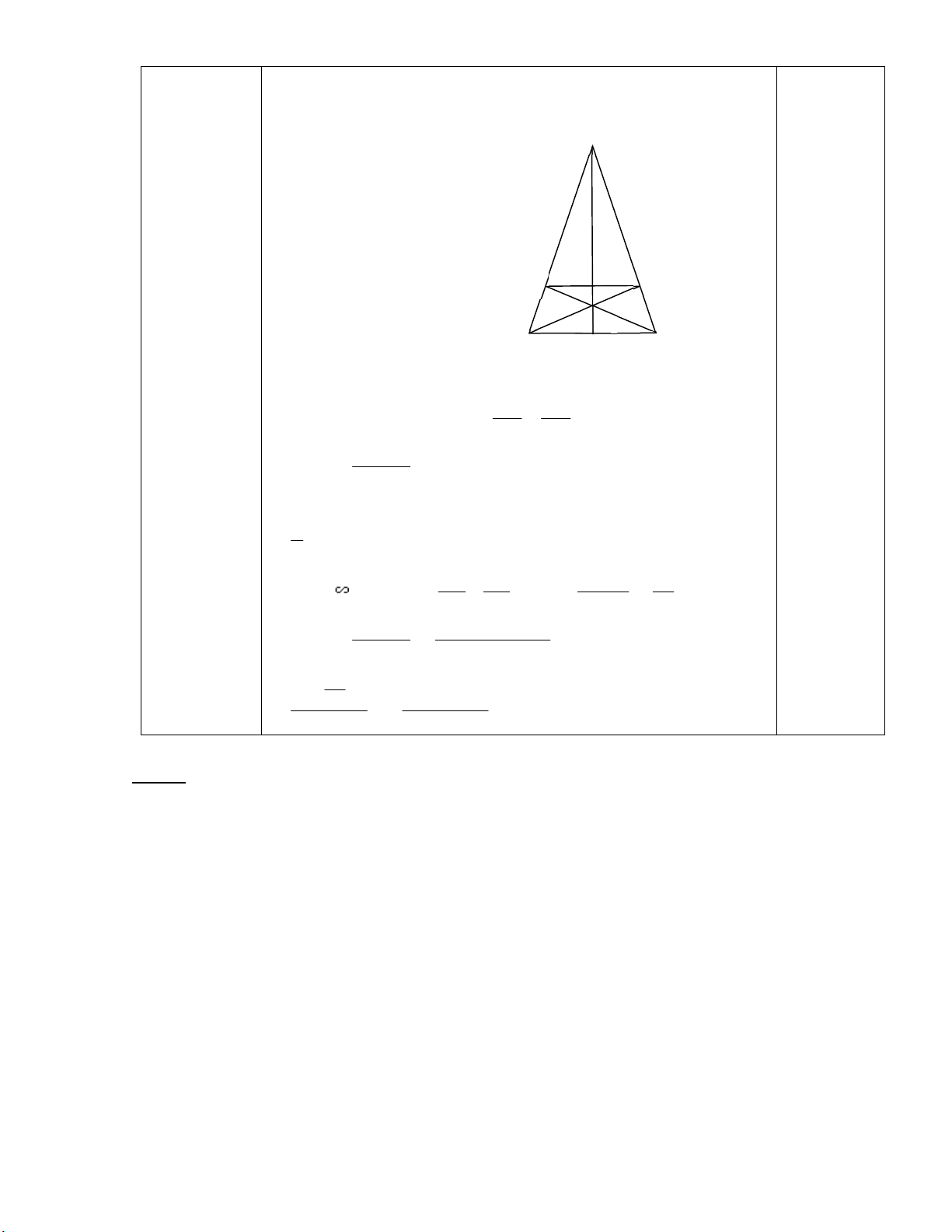
Khi AB = AC = b thì ABC cân tại A 0,25đ Suy ra được DE // BC DE AD   BC AC  DE = A . D BC 0,25đ AC
Gọi giao điểm của AH và BC là F  AF  BC, FB = FC = a 0,25đ 2 2 DBC FAC DC BC   B . C FC  a DC  = 0,5đ FC AC AC 2b  DE = A . D BC = (AC  DC).BC 0,25đ AC AC 2 a (b  ).a 2 2 = 2b = a(2b  a ) 0,5đ b 2 2b
Lưu ý: - Bài hình học sinh không vẽ hình hoặc vẽ hình sai không chấm điểm.
- Học sinh làm cách khác đúng vẫn cho điểm tối đa.