Đề Thi HSG Toán 8 Huyện Lâm Thao 2025-2026 Có Đáp Án

PHÒNG GD&ĐT LÂM THAO KỲ THI CHỌN HỌC SINH GIỎI LỚP 6,7,8 CẤP HUYỆN
NĂM HỌC 2025 – 2026 ĐỀ CHÍNH THỨC MÔN THI: TOÁN 8
Thời gian làm bài: 120 phút không kể thời gian phát đề
(Đề thi gồm 02 trang)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (8 điểm) Câu 1. Cho đa thức 4 3 2
x − 9x + 21x + ax + b chia hết cho đa thức 2
x − x − 2 . Khi đó a − b bằng A. 29 . B. 31. C. −29 . D. −31. Câu 2. Cho đa thức 3 2
P(x) = 2x + ax + x + b chia cho đa thức 2x + 3 được thương là 2
Q(x) = x − 3x + 5 và số dư r = 20 . Giá trị của 2a + 3b bằng A. −111. B. 111. C. 101. D. 99 . − +
Câu 3. Giá trị lớn nhất của biểu thức 6x 8 F = bằng 2 −x −1 A. 1. B. 9 − . C. 3 . D. 1 − .
Câu 4. Cho ba số thực x; y; z thỏa mãn 2 2 2
4x + 2y + 2z − 4xy − 4xz + 2yz − 6y −10z + 34 = 0.
Giá trị của biểu thức A = (x − )2022 + ( y − )2023 2024 4 4 + (z − 6) là A. 3 . B. 0 . C. 1. D. 2 . 2 2 x + y 8 2 2
x − 5xy + y Câu 5. Cho
= ; x, y  0. Giá trị của phân thức P = bằng xy 5 2 2
x + 3xy + y − − A. 15 . B. 18 . C. 18. D. 17 . 23 23 23 23 + Câu 6. Cho a b 17x 18 + =
. Giá trị của 2a + b bằng 2 x − 2 3x + 7 3x + x −14 A. 13. B. 12 . C. 10 . D. 14 .
Câu 7. Với giá trị nào của m thì phương trình: 2mx(x −1) − x(3x +1) + 2023 = 0 là phương
trình bậc nhất một ẩn ? A. 3 m  . B. 3 m = . C. 1 m = . D. 1 m  . 2 2 2 2
Câu 8. Cho phương trình 2
9x + 3 = m x + m (với m là tham số, m  ). Số các giá trị của m để
phương trình có nghiệm nguyên duy nhất là A. 2 . B. 4 . C. 1. D. 0 .
Câu 9. Cho tam giác ABC cân tại A, AB = 32c ,
m BC = 24cm . Gọi K là hình chiếu của B trên
AC. Độ dài đoạn thẳng KC bằng A. 8cm . B. 9cm .
C. 10cm .
D. 11cm .
Câu 10. Cho tam giác ABC có diện tích bằng 1. Các đường trung tuyến AD, BE,CF. Diện
tích của tam giác có độ dài ba cạnh bằng độ dài ba đường trung tuyến AD, BE,CF là A. 3 . B. 4 . C. 5 . D. 2 . 4 3 6 3
Câu 11. Một hình thoi có độ dài một cạnh là 10cm và độ dài một đường chéo là 16cm có diện tích là A. 2 96cm . B. 2 128cm . C. 2 64cm . D. 2 24cm .
Câu 12. Mỗi góc của một đa giác đều, có số đo là 0
135 . Số đường chéo của đa giác đều đó là A. 35 . B. 14 . C. 20 . D. 27. Trang 1
Câu 13. Một bể hình hộp chữ nhật có chiều dài và chiều rộng tỉ lệ với 4 và 3. Chiều cao
bằng một nửa chiều dài. Thể tích của bể là 3
192m . Chiều cao của bể là A. 6m . B. 3m . C. 5 . m D. 4 . m
Câu 14. Cho hình hình bình ABCD, đường thẳng qua A cắt BD,CD, BC lần lượt tại E, I, K.
Khi đó đẳng thức nào sau đây đúng ? A. 2
AE = EI.IK .
B. AE.AI = EI.EK . C. 2
AE = EI.EK .
D. AE. AI = KE .KI .
Câu 15. Cho tam giác ABC vuông tại ;
A đường cao AH ⊥ BC, (H  BC) . Biết BH = 18c ; m CH = 32 c .
m Chu vi tam giác ABC bằng
A. 150cm .
B. 120cm . C. 130 . cm D. 140 . cm
Câu 16. Một đoàn người đi thăm quan Đền Hùng bằng ô tô. Nếu mỗi xe đi 27 người thì còn
thừa 4 chỗ ngồi. Nếu bớt đi một xe thì số người được chia đều cho các xe. Mỗi xe đi không
quá 29 người. Số người trong đoàn tham quan là A. 621 . B. 625 . C. 648 . D. 644 .
PHẦN II. TỰ LUẬN (12 điểm) Câu 1. (3 điểm)
1. Cho các số nguyên x, y, z thỏa mãn 2x + y, 2y + z, 2z + x đều là các số chính phương.
Biết (2x + y)(2y + z)(2z + x) 3. Chứng minh rằng
a) Các số 2x + y, 2y + z, 2z + x đều chia hết cho 3.
b) ( x − y)3 + ( y − z)3 + ( z − x)3 81.
2. Giải phương trình nghiệm nguyên: 3 2
x − x − 7x +10 = y (với x, y là các số nguyên tố). Câu 2. (4 điểm)
1. Giải phương trình: (x + )3 + (x − )3 = (x + )3 18 4 8 7 . 4 2 2 − + −
2. Giải phương trình: 3x 8x 6 3 4x ( + = x − ) 1. 2 4 2 x +1 1 Câu 3. (4 điểm)
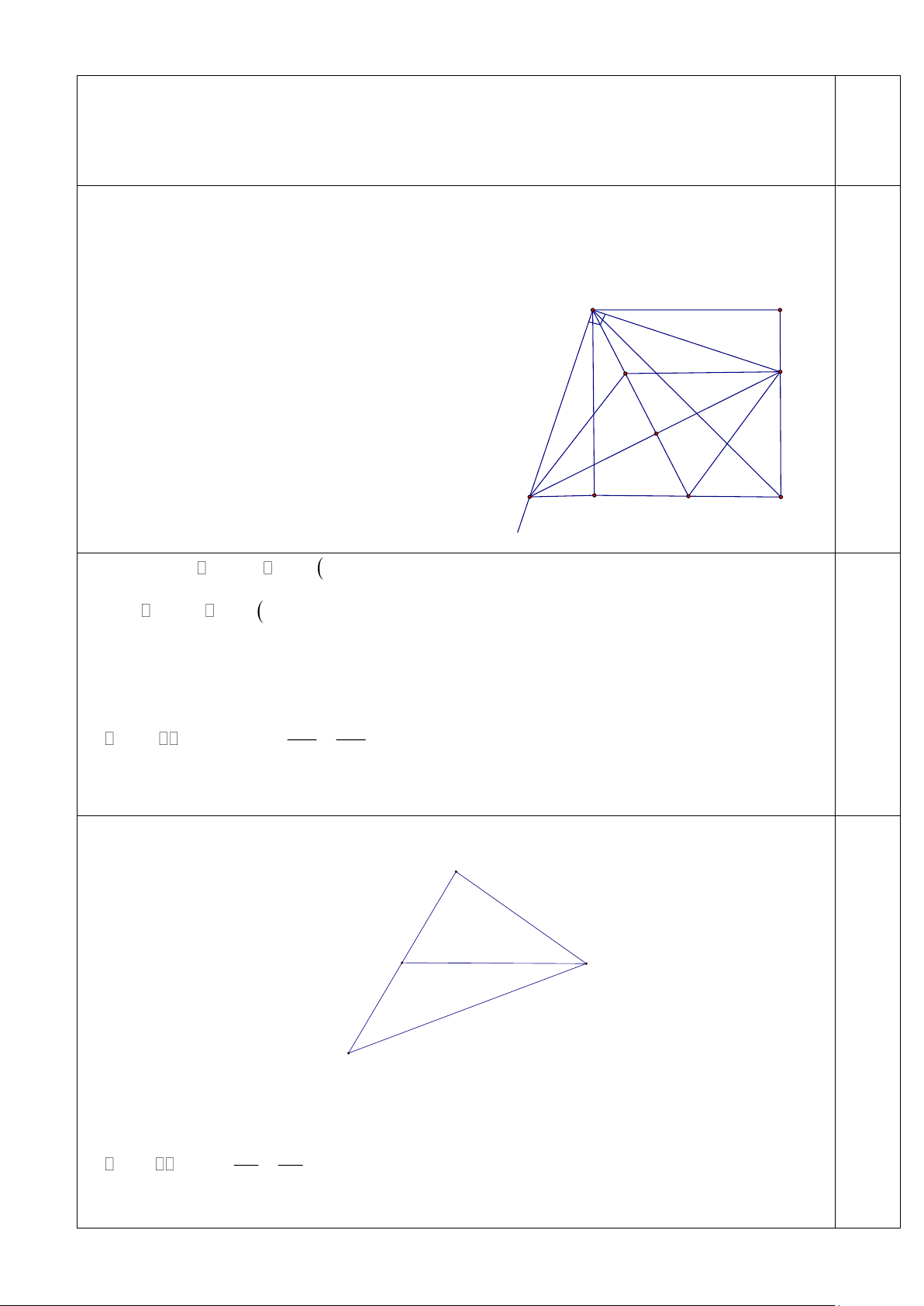
1. Cho hình vuông MNP .
Q Gọi A là một điểm trên cạnh .
NP Qua M kẻ tia Mx vuông góc với ,
MA tia Mx cắt đường thẳng PQ tại B. Trung tuyến MD của tam giác MAB cắt cạnh PQ ở C. Đường thẳng qua ,
A song song với MN cắt MD ở E. Chứng minh rằng
a) MA = MB và tứ giác AEBC là hình thoi. b) 2 MA = E . A P . B
2. Cho tam giác IHK có độ dài ba cạnh là ba số tự nhiên liên tiếp. Tính diện tích của tam giác IHK biết K = 2H. Câu 4. (1 điểm) Cho 1 1 1 a, ,
b c  0 thỏa mãn a + b + c = 3 . Chứng minh rằng: + + 1. 2 2 2
2 + a b 2 + b c 2 + c a
------------------------------ Hết-----------------------------
- Họ và tên thí sinh :....................................................... Số báo danh .............................
- Cán bộ coi thi không giải thích gì thêm. Trang 2
PHÒNG GD&ĐT LÂM THAO KỲ THI CHỌN HỌC SINH GIỎI LỚP 6,7,8 CẤP HUYỆN
NĂM HỌC 2022 – 2023
HƯỚNG DẪN CHẤM MÔN TOÁN 8
I. Một số chú ý khi chấm bài
- Hướng dẫn chấm thi dưới đây dựa vào lời giải sơ lược của một cách. Khi chấm thi giám
khảo cần bám sát yêu cầu trình bày lời giải đầy đủ, chi tiết, hợp logic và có thể chia nhỏ đến 0,25 điểm.
- Thí sinh làm bài theo cách khác với hướng dẫn chấm mà đúng thì tổ chấm cần thống nhất
cho điểm tương ứng với thang điểm của hướng dẫn chấm.
- Điểm bài thi là tổng điểm các câu không làm tròn số.
II. Đáp án – thang điểm
1. Phần trắc nghiệm khách quan: Mỗi câu trả lời đúng được 0,5 điểm. Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 B D A B D A B A Câu 9 Câu 10 Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 B A A C D C B D 2. Phần tự luận: Nội dung Điểm Câu 1.
1. Cho các số nguyên x, y, z thỏa mãn 2x + y, 2y + z, 2z + x đều là các số chính phương.
Biết (2x + y)(2y + z)(2z + x) 3. Chứng minh rằng: a) Các số 3,0
2x + y , 2 y + z và 2z + x đều chia hết cho 3.
b) ( x − y)3 + ( y − z)3 + ( z − x)3 81.
2. Giải phương trình nghiệm nguyên: 3 2
x − x − 7x +10 = y (với x, y là các số nguyên tố). 1.
a. Ta có (2x + y) + (2y + z) + (2z + x) = 3(x + y + z) 3 . 0,25
Vì một số chính phương chia 3 dư 0 hoặc 1 mà (2x + y)(2y + z)(2z + x) 3 0,25 2x + y 3   0,25 2y + z 3 2z + x 3 
b. ( x − y)3 + ( y − z)3 + ( z − x)3 81. 2x + y 9 
 2y + z 9  3(x + y + z) 9  x + y + z 3  0,25 2z + x 9  Trang 3 x − y 3 
 y − z 3 0,25 z − x 3  0,25
Mà ( x − y)3 + ( y − z)3 + ( z − x)3 = 3(x − y)( y − z)(z − x) 81. 2. Ta có 3 2
x − x − 7x +10 = y  (x − )( 2
2 x + x − 5) = y 0,5
Để y là số nguyên tố thì x − 2 = 1 hoặc 2 x + x − 5 = 1 0,25
Nếu x − 2 = 1 x = 3, khi đó y = ( − )( 2
3 2 3 + 3 − 5) = 7 (thỏa mãn) 0,25 Nếu 2
x + x − 5 = 1 x(x +1) = 6  x = 2 , khi đó y = ( − )( 2
2 2 2 + 2 − 5) = 0 ( loại) 0,25 Vậy ( ; x y) = (3;7) 0,25 Câu 2.
a) Giải phương trình: (x + )3 + (x − )3 = (x + )3 18 4 8. 7 . 4,0 4 2 2
3x − 8x + 6 3 − 4x b) Giải phương trình: ( + = x − ) 1. 2 4 2 x +1 1
a) (x + )3 + (x − )3 = (x + )3  (x + )3 + (x − )3 + (− x − )3 18 4 8. 7 18 4 2 14 = 0 0,5 0,5 Vì x +
+ x − − x −
=  (x + )3 + (x − )3 + (− x − )3 18 4 2 14 0 18 4 2
14 = 3(x +18)(x − 4)( 2 − x −14)
 3(x +18)(x − 4)( 2 − x −14) = 0 0,5
Vậy tập nghiệm của phương trình S =  1 − 8;4;−  7 0,5 4 2 2
3x − 8x + 6 3 − 4x b) ( + = x − ) 1. 2 4 2 x +1 1 4 2 3x − 8x + 6 Chỉ ra được 0,5 (
 . Dấu “=” xảy ra x =  2 x − ) 2 2 2 1 2 3 − 4x 0,5 Chỉ ra được  1
− . Dấu “=” xảy ra x =  2 4 x +1 4 2 2
3x − 8x + 6 3 − 4x Suy ra 0,5 ( +
 . Dấu “=” xảy ra x =  2 . x − ) 1 2 4 2 x +1 1
Vậy tập nghiệm của phương trình là S = − 2; 2 0,5 Câu 3.
1. Cho hình vuông MNP .
Q Gọi A là một điểm trên cạnh NP .Qua M kẻ tia Mx vuông góc với ,
MA tia Mx cắt đường thẳng PQ tại B. Trung tuyến MD của tam giác MAB cắt cạnh PQ ở C. 4,0 Đường thẳng kẻ qua ,
A song song với MN cắt MD ở E. Chứng minh rằng:
a) MA = MB và tứ giác AEBC là hình thoi. b) 2 MA = E . A P . B Trang 4
2. Cho tam giác IHK có độ dài ba cạnh là ba số tự nhiên liên tiếp. Tính diện tích của tam
giác IHK biết K = 2H.
1. Cho hình vuông MNP .
Q Gọi A là một điểm trên cạnh NP .Qua M kẻ tia Mx vuông góc với ,
MA tia Mx cắt đường thẳng PQ tại B. Trung tuyến MD của tam giác MAB cắt cạnh PQ ở C. Đường thẳng kẻ qua ,
A song song với MN cắt MD ở E. Chứng minh rằng:
a) MA = MB và tứ giác AEBC là hình thoi. M N b) 2 MA = E . A P . B E A D B Q C P x
a) Chỉ ra MNA = MQB (g. .
c g )  MA = MB 0,5
Chỉ ra ADE = BDC (g. .
c g )  AE = BC mà AE / /BC  tứ giác AEBC là hình bình hành 0,5
Chỉ ra được MD ⊥ AB suy ra tứ giác AEBC là hình thoi. 0,5 b) Chỉ ra được 0 MPC = BMC = 45 0,5 MB PB  MPB
CMB (g.g)  = CB MB 0,5 2  MB = C . B PB mà 2 MB = M ,
A EA = CB  MA = E . A PB 0,5
2. Cho tam giác KHI có độ dài ba cạnh là ba số tự nhiên liên tiếp. Tính diện tích của tam
giác KHI biết K = 2H. I K H A
Trên tia đối của tia KI lấy điểm A sao cho KA = KH  KAH = IHK 0,25 IK IH 2 2 2  IKH IHA  =
 IK.IA = IH  IK + IK.KH = IH IH IA Trang 5
IK.KH = (IH − IK )(IH + IK ) 0,25
TH1: IH − IK = 1 IK.KH = IH + IK = 2IK +1 IK (KH − 2) =1 IK =1; IH = 2; KH = 3 0,25
TH2: IH − IK = 2  IK.KH = 2(IH + IK ) = 4IK + 4  IK (KH − 4) = 4  IK = 4; IH = 6; KH = 5 0,25
Diện tích của tam giác IHK là 15 7 (đvdt) 4 Câu 4. 1,0 Cho 1 1 1 a, ,
b c  0 thỏa mãn a + b + c = 3 . Chứng minh rằng: + +  1. 2 2 2 2 + a b 2 + b c 2 + c a Đặt 1 1 1 + + = P 2 2 2 2 + a b 2 + b c 2 + c a 2 2 2  2   2   2 a b b c c a Ta có 
Q = 3 − 2P = 1− + 1− + 1− = + +  0,25 2   2   2  2 2 2  2 + a b   2 + b c  
2 + c a  2 + a b 2 + b c 2 + c a
Áp dụng bất đẳng thức Cauchy ta có 2 2 3 4 2 3 2 a b a b a b a ab
a a + b + b a + 2ab 2 2 2 ( ) 2 3
2 + a b = 1+1+ a b  3 a b   = =  = (1) 2 3 2 2 + a b 3 3 9 9 3 a b 0,25 2 2 2 2 b c b + 2cb c a c + 2ca 0,25 Tương tự  (2);  (3); 2 2 2 + b c 9 2 + c a 9 2
(a + b + c)
Từ (1), (2), (3)  Q 
= 1nên 3 − 2P  1  P  1 0,25 9
a + b + c = 3  Dấu “=” xảy ra khi 2 2 2
a b = b c = c a = 1  a = b = c = 1
a = b = c  0  Trang 6