Đề thi HSG Toán 8 năm 2014 – 2015 phòng GD&ĐT Tam Đảo – Vĩnh Phúc

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề thi HSG Toán 8 năm 2014 – 2015 phòng GD&ĐT Tam Đảo – Vĩnh Phúc; đề thi có lời giải chi tiết và hướng dẫn chấm điểm.

55 28 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 8

Môn: Toán 8

Thông tin:

4 trang 4 tháng trước

Tác giả:

Profile Mai Nguyệt
PHÒNG GD&ĐT TAM ĐẢO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
NĂM HỌC 2014-2015
MÔN: TOÁN 8
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
Câu 1( 2,0 điểm):
Cho biểu thức: M=
3 6 2
6 5 2 9 6 3
6 2 4 6 24 3 3
1 . : :
2
9 3 6 9
x x x
x
x x x x x x
a) Rút gọn M.
b) Tìm các giá trị nguyên của
x
để M đạt giá trị lớn nhất. Tìm giá trị lớn nhất
đó.
Câu 2( 2,0 điểm):
Giải các phương trình và bất phương trình sau:
a)
1 2 3 1
2015 2014 1006 2013 2012 1007
x x x x
b)
2
2 3
1
1 1
y
y
y y y
Câu 3( 2,5 điểm):
a) Cho ba số
, ,
x y z
khác không thỏa mãn:
2015
1 1 1 1
2015
x y z
x y z
Chứng minh rằng trong ba số
, ,
x y z
tồn tại hai số đối nhau.
b) Cho ba số dương
, ,
a b c
. Chứng minh rằng:
2 2 2
2
a b c a b c
b c c a a b
Câu 4( 2,5 điểm):
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC
(M khác B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao
cho BE = CM.
a) Chứng minh: ∆OEM vuông cân.
b) Chứng minh: ME // BN.
c) Từ C kẻ CH
BN ( H
BN). Chứng minh ba điểm O, M, H thẳng hàng.
Câu 5( 1 điểm):
Tìm giá trị nhỏ nhất của biểu thức:
2 2
5 2 4 2 4 2015
x y xy x y
.
----------Hết----------
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
NĂM HỌC 2014 - 2015
Môn: Toán - Lớp 8
Câu
Ý
N
ội dung
Đi
ểm
1
(2,0
điểm)
a
ĐKXĐ:
3 3
0; 3; 2.
x x x
3 6 2
6 5 2 9 6 3
3 2
3 3
3 2 2 2 3 3 6 3
3 2
3 2 3 3 3 2 3
6 2 4 6 24 3 3
1 . : :
2
9 3 6 9
6 ( ) 4
2( 3) 4 3( 2)
1 . : :
2
( ) 3 ( 3) ( 6 9)
6 ( ) 4
2 4 2
1 . : .
3 ( 3) ( 3) 3(
x x x
M
x
x x x x x x
x
x x
x
x x x x x x
x
x
x x x x x x
3 2 3 2 3
3 2 3 3 3
2)
5 4 .( 3) 5
. .
3 ( 3) 4( 2) 2
x x x x
x x x x x
0,25
0,25
0,25
0,25
b
Ta có:
3
3 3
5 7
1
2 2
x
M
x x
M có giá trị lớn nhất khi
3
2
x
có giá trị nhỏ nhất mà
x Z
nên
3
2
x
phải có giá trị nguyên dương nhỏ nhất
3
2
x
=6
2
x
Vậy
2
x
thì M có giá trị lớn nhất và bằng
13
6
0,25
0, 5
0,25
2
(2,0
điểm)
a
1 2 3 1
2015 2014 1006 2013 2012 1007
1 2 2 2 3 4 4 1
2015 2014 2014 1006 2013 2012 2012 1007
1 2 1 4 3 4 4 1
2015 2014 1007 2012 2013 2012 2012 1007
1 2 3 4
1 1 1 1
2015 2014 2013 2012
2016
20
x x x x
x x x x
x x x x
x x x x
x
2016 2016 2016
15 2014 2013 2012
1 1 1 1
( 2016)( ) 0 2016
2015 2014 2013 2012
x x x
x x
0,25
0,25
0,25
0,25
b
ĐK: y
1
2 2 2
2 3 2 3
2
3 3 2
2
4 1 2 5 4(1 ) 1 2 5
0
1
1 1 (1 )(1 ) 1
3 3 3 ( 1) 3 ( 1)
0 0 0
1 1 (1 )(1 )
3
0 3 0 0
1
y y y y y
y
y y y y y y y
y y y y y y
y y y y y
y
y y
y y
Vậy nghiệm của bất phương trình đã cho là
0
1
y
y
0,25
0,25
0,25
0,25
3
(2,5
điểm)
a
2 2
2
1 1 1
( )( ) 1
( )( ) 0
( ) ( )( ) ( ) 0
( ) ( ) ( ) 0
( )( ) 0
0
( ( )( ) 0 0
0
x y z
x y z
x y z xy yz zx xyz
x xy xz xyz y z xy xz yz y z xyz
x y z x y z yz y z
y z x xy xz yz
x y x y
x y y z z x y z y z
z x z x
Vậy trong ba số
, ,
x y z
tồn tại hai số đối nhau
0,25
0,25
0,25
0,25
0,25
b
Ta có:
2 2 2 2
( )
, ,
a b c a b c
x y z
x y z x y z
>0 (1)
Thật vậy, áp dụng BĐT Bunhiacopxki ta có:
2 2 2
2 2 2 2 2 2
2
2
( )( )
( ) ( ) ( ) ( ) ( ) ( )
. . . ( )
a b c
x y z
x y z
a b c
x y z
x y z
a b c
x y z a b c
x y z
2 2 2 2
( )
, ,
a b c a b c
x y z
x y z x y z
>0.
Áp dụng BĐT (1) ta có:
2 2 2 2
( )
, , 0
2( ) 2
a b c a b c a b c
a b c
b c c a a b a b c
ĐPCM. Dấu “=” xảy ra
a=b=c
0,25
0,25
0,25
0,25
0,25
4
(2,5
điểm)
a
Xét ∆OEB và ∆OMC
Vì ABCD là hình vuông nên ta có OB = OC
0,25
M
N
C
H
D
O
E BA
Và
0
45
EBO MCO
BE = CM ( gt )
Suy ra ∆OEB = ∆OMC ( c .g.c)
OE = OM và
EOB MOC
Lại có
2 3
O O
0
90
BOC
vì tứ giác ABCD là hình vuông
0
90
EOM EOB MOB MOC MOB COB
kết hợp với OE =
OM
∆OEM vuông cân tại O
0,25
0,25
b Từ (gt) tứ giác ABCD là hình vuông
AB = CD và AB // CD
+ AB // CD
AB // CN
AM BM
MN MC
( Theo ĐL Ta- lét) (*)
Mà BE = CM (gt) và AB = CD
AE = BM thay vào (*)
Ta có :
AM AE
MN EB
ME // BN ( theo ĐL đảo của ĐL Ta-lét)
0,25
0,25
0,25
c
Gọi H’ là giao điểm của OM và BN
Từ ME // BN
'
OME MH B
( cặp góc đồng vị)
Mà
0
45
OME
vì ∆OEM vuông cân tại O
0
' 45
MH B MCO
∆OMC
∆BMH’ (g.g)
'
OM MC
MB MH
,kết hợp
'
OMB CMH
( hai góc đối đỉnh)
∆OMB
∆CMH’ (c.g.c)
0
' 45
OBM MH C
Vậy
0
' ' ' 90
BH C BH M MH C
'
CH BN
Mà CH
BN ( H
BN)
H
H’ hay 3 điểm O, M, H thẳng hàng
0,5
0,5
5
(1,0
điểm)
Ta có:
2 2
5 2 4 2 4 2015
x y xy x y
2 2 2 2
2 2 2
4 4 4 4 2 1 2010
(2 ) ( 2) ( 1) 2010 2010 , ,
x xy y y y x x
x y y x x y z
Vậy Min(A)=2010
1
2
x
y
0,25
0,5
0,25
Tổng điểm 10,0
---------------------HÕt------------------------
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GD&ĐT TAM ĐẢO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI NĂM HỌC 2014-2015 MÔN: TOÁN 8
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Câu 1( 2,0 điểm): 3 6 2  6  2x  4  6x  24  3x 3  Cho biểu thức: M= 1 . :  :    6 5 2 9 6 3  x  9  x  3x x  6x  9x 2 x    a) Rút gọn M.
b) Tìm các giá trị nguyên của x để M đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó. Câu 2( 2,0 điểm):
Giải các phương trình và bất phương trình sau: x 1 x 2 x  3 x 1 a)      2015 2014 1006 2013 2012 1007 2 4 1 2 y  5 b)   2 3 1  y  y 1  y y 1 Câu 3( 2,5 điểm):  x  y  z  2015 a) Cho ba số 
x, y, z khác không thỏa mãn:  1 1 1 1     x y z 2015
Chứng minh rằng trong ba số x, y, z tồn tại hai số đối nhau. 2 2 2 a b c a  b  c
b) Cho ba số dương a,b,c . Chứng minh rằng:    b  c c  a a  b 2 Câu 4( 2,5 điểm):
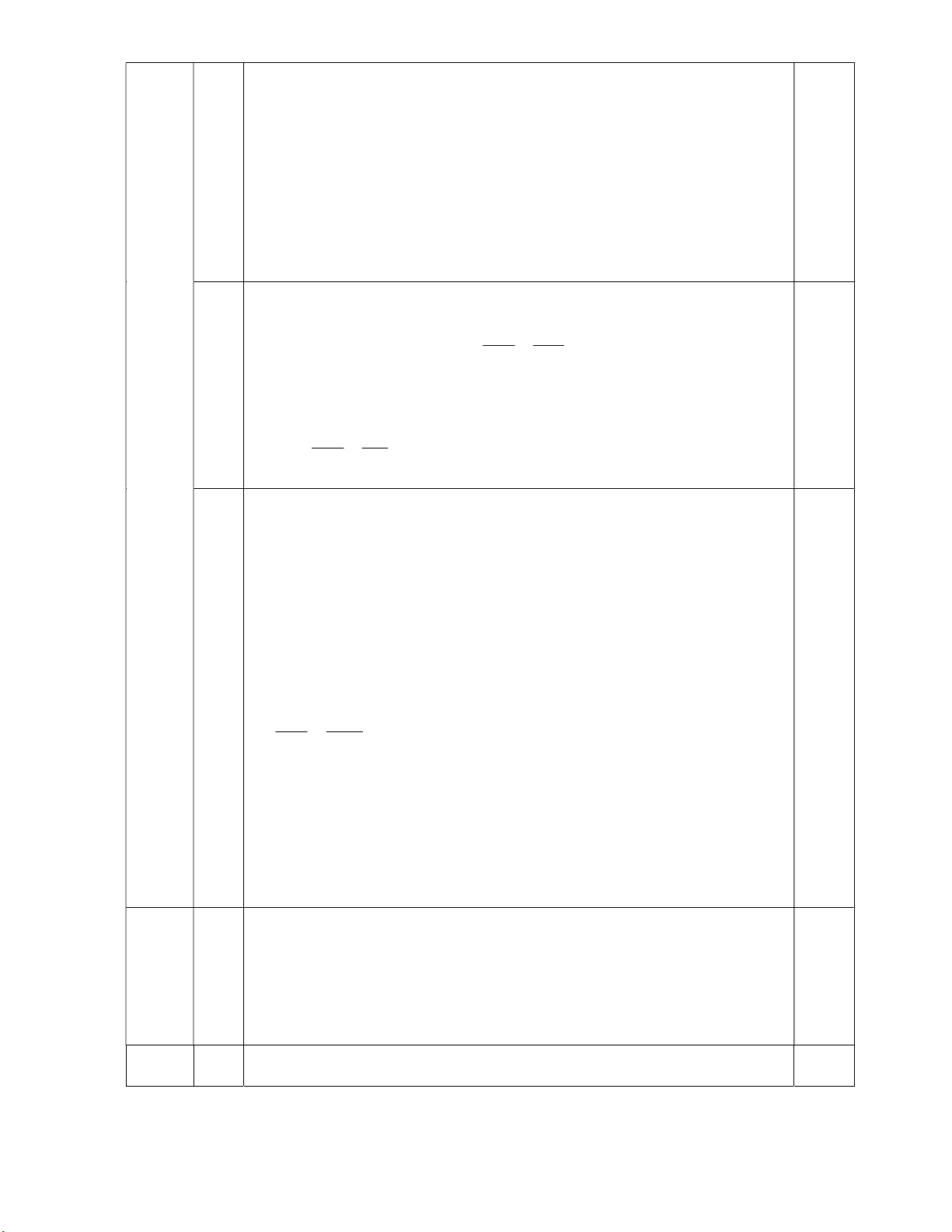
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC
(M khác B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh: ∆OEM vuông cân. b) Chứng minh: ME // BN.
c) Từ C kẻ CH  BN ( H  BN). Chứng minh ba điểm O, M, H thẳng hàng. Câu 5( 1 điểm):
Tìm giá trị nhỏ nhất của biểu thức: 2 2
5x  2y  4xy  2x  4y  2015 . ----------Hết----------
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI NĂM HỌC 2014 - 2015 Môn: Toán - Lớp 8 Câu Ý Nội dung Điểm a ĐKXĐ: 3 3 x  0; x  3  ; x  2. 0,25 3 6 2  6  2x  4  6x  24  3x 3  M  1 . :  :    6 5 2 9 6 3  x  9  x  3x x  6x  9x 2 x    3 2 3        3 6 (x ) 4 2(x 3) 4    3(x  2)    1 . :  :  0,25 3 2 2 2 3 3 6 3   
(x )  3  x (x  3)  x (x  6x  9) 2x     3 2 6 (x )  4  2  4    2x  1  1 . :  .   0,25 3  2 3 3 3 2 3 
x  3  x (x  3)  x (x  3) 3(x  2)  (2,0   điểm) 3 2 3 2 3 x  5 4 x .(x  3) x  5  . .  3 2 3 3 3 x  3 x (x  3) 4(x  2) x  2 0,25 b 3 x  5 7 Ta có: M   1 3 3 x  2 x  2 0,25
M có giá trị lớn nhất khi 3
x  2 có giá trị nhỏ nhất mà x  Z nên 3
x  2 phải có giá trị nguyên dương nhỏ nhất  3 x  2 =6  x  2 0, 5
Vậy x  2 thì M có giá trị lớn nhất và bằng 13 6 0,25 a x 1 x 2 x  3 x 1      2015 2014 1006 2013 2012 1007 x 1 x  2 2 2 x  3 x  4 4 1 0,25         2015 2014 2014 1006 2013 2012 2012 1007 x 1 x  2 1 4 x  3 x  4 4 1         2015 2014 1007 2012 2013 2012 2012 1007 0,25 x 1 x  2 x  3 x  4  1 1  1 1 2015 2014 2013 2012 0,25 x  2016 x  x  x  2  2016 2016 2016    2015 2014 2013 2012 (2,0 1 1 1 1 điểm)  (x  2016)(    )  0  x  2016 0,25 2015 2014 2013 2012 b ĐK: y  1 2 2 2 4 1 2 y  5 4(1 y) 1  y  y 2 y  5      0 2 3 2 3 1 y  y 1 y y 1 (1 y  y )(1 y) 1  y 0,25 2 3y  3y 3y( y 1) 3y( y 1)   0   0   0 0,25 3 3 2 1  y 1 y (1 y)(1 y  y ) 3y   0  3  y  0  y  0 2 1 y  y 0,25  y  0
Vậy nghiệm của bất phương trình đã cho là  0,25  y  1 a 1 1 1 (x  y  z)(   )  1 0,25 x y z
 (x  y  z)(xy  yz  zx)  xyz  0
 x(xy  xz)  xyz  ( y  z)(xy  xz)  yz( y  z)  xyz  0 0,25 2 2
 x ( y  z)  x( y  z)  yz(y  z)  0 0,25 2
 (y  z)(x  xy  xz  yz)  0 x  y  0 x   y (x y( y z)(z x) 0  y z 0           y  z   0,25 z  x  0 z  x  
Vậy trong ba số x, y, z tồn tại hai số đối nhau 0,25 b 2 2 2 2 Ta có: a b c (a  b  c)    x  , y, z >0 (1) x y z x  y  z 0,25 3 (2,5
Thật vậy, áp dụng BĐT Bunhiacopxki ta có: điểm) 2 2 2 a b c (x  y  z)(   ) x y z   2 2 2 a 2 b 2 c 2
 ( x)  ( y)  ( z )  ( )  ( )  ( )  0,25    x y z   2  a b c  2   x.  y.  z.   (a  b  c)  x y z   2 2 2 2 a b c (a  b  c)     x  , y, z >0. 0,25 x y z x  y  z Áp dụng BĐT (1) ta có: 2 2 2 2 a b c (a  b  c) a  b  c     a  , , b c  0 0,25 b  c c  a a  b 2(a  b  c) 2
 ĐPCM. Dấu “=” xảy ra  a=b=c 0,25 a A E B H M 4 0,25 (2,5 O điểm) N D C Xét ∆OEB và ∆OMC
Vì ABCD là hình vuông nên ta có OB = OC Và  EBO   0 MCO  45 BE = CM ( gt )
Suy ra ∆OEB = ∆OMC ( c .g.c)  OE = OM và  EOB   MOC 0,25 Lại có  O   O   0
BOC  90 vì tứ giác ABCD là hình vuông 2 3  EOM   EOB   MOB   MOC   MOB   0
COB  90 kết hợp với OE =
OM  ∆OEM vuông cân tại O 0,25 b
Từ (gt) tứ giác ABCD là hình vuông  AB = CD và AB // CD 0,25 + AB // CD  AB // CN  AM BM  ( Theo ĐL Ta- lét) (*) MN MC
Mà BE = CM (gt) và AB = CD  AE = BM thay vào (*) 0,25 Ta có : AM AE 
 ME // BN ( theo ĐL đảo của ĐL Ta-lét) 0,25 MN EB c
Gọi H’ là giao điểm của OM và BN Từ ME // BN   OME  
MH ' B ( cặp góc đồng vị) Mà  0
OME  45 vì ∆OEM vuông cân tại O   0 MH ' B  45   MCO
 ∆OMC  ∆BMH’ (g.g) 0,5 OM MC   ,kết hợp  OMB  
CMH ' ( hai góc đối đỉnh) MB MH '
 ∆OMB  ∆CMH’ (c.g.c)   OBM   0 MH 'C  45 Vậy  BH C   BH M   0 ' ' MH 'C  90  CH '  BN
Mà CH  BN ( H  BN)  H  H’ hay 3 điểm O, M, H thẳng hàng 0,5 Ta có: 2 2
5x  2y  4xy  2x  4y  2015 0,25 5 2 2 2 2 (1,0
4x  4xy  y  y  4y  4  x  2x 1  2010 0,5 điểm) 2 2 2
 (2x  y)  ( y  2)  (x 1)  2010  2010 , x y, z Vậy Min(A)=2010   x  1 0,25  y    2 Tổng điểm 10,0
---------------------HÕt------------------------