PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN VÒNG 2 XUÂN TRƯỜNG NĂM HỌC 2023-2024 Môn: Toán - Lớp 8 THCS
(Thời gian làm bài 120 phút) ĐỀ CHÍNH THỨC Đề thi gồm: 02 trang. Câu 1: (4,0 điểm)
1) Cho hai số thực dương a,b thay đổi thỏa mãn đẳng thức a  b  1. Tính giá trị của biểu thức 3 3 a  5ab  b A  . a b2 8ab 1
2) Cho các số thực thay đổi x, y, z khác 0 thỏa mãn x  y  z  0 . 2 2 2 x y z 3 Chứng minh rằng :    . 2 2 2 2 2 2 2 2 2 x  y  z y  x  z z  x  y 2 Câu 2: (3,5 điểm) 3 3
1) Tìm các số thực x thỏa mãn đẳng thức x     x  3 2   2 1 5 7 x  5x  6 .
2) Tìm phần dư trong phép chia đa thức P  x cho đa thức  x  
1  x  2 . Biết rằng đa thức P x chia cho đa thức  x  
1 dư là 7, chia cho đa thức  x  2 dư là 1. Câu 3: (3,5 điểm)
1) Một trường THCS có tổ chức cho các em học sinh khối 8 và khối 9 đi trải nghiệm bằng ô tô. Nếu mỗi
xe chỉ chở 22 học sinh thì còn thừa một học sinh. Nếu bớt đi một xe ô tô thì có thể phân phối đều số học
sinh vào các xe còn lại. Hỏi lúc đầu có bao nhiêu xe ô tô và có tất cả bao nhiêu học sinh đi trải nghiệm ?
Biết rằng số học sinh trên mỗi xe không vượt quá 32 em. 2 2 a  b a
2) Cho a,b, c là các số nguyên khác 0, a  c sao cho  . Chứng minh rằng 2 2 2 a  b  c không 2 2 b  c c phải số nguyên tố. Câu 4: (7,0 điểm)
1) Cho tam giác ABC nhọn, không cân, các đường cao BD và CE cắt nhau ở H . Gọi I, J , K lần lượt
là trung điểm của BC, DE, AH . a. Chứng minh A .
D AC  AE.AB và ba điểm I , J , K thẳng hàng.
b. Gọi X là giao điểm của ba đường trung trực của tam giác ABC . Gọi Y , Z lần lượt là hình chiếu của X trên các cạnh C , A AB theo thứ tự đó. Chứng minh rằng 3 3 3 HA  HB  HC   3 3 3 8 XI  XY  XZ 
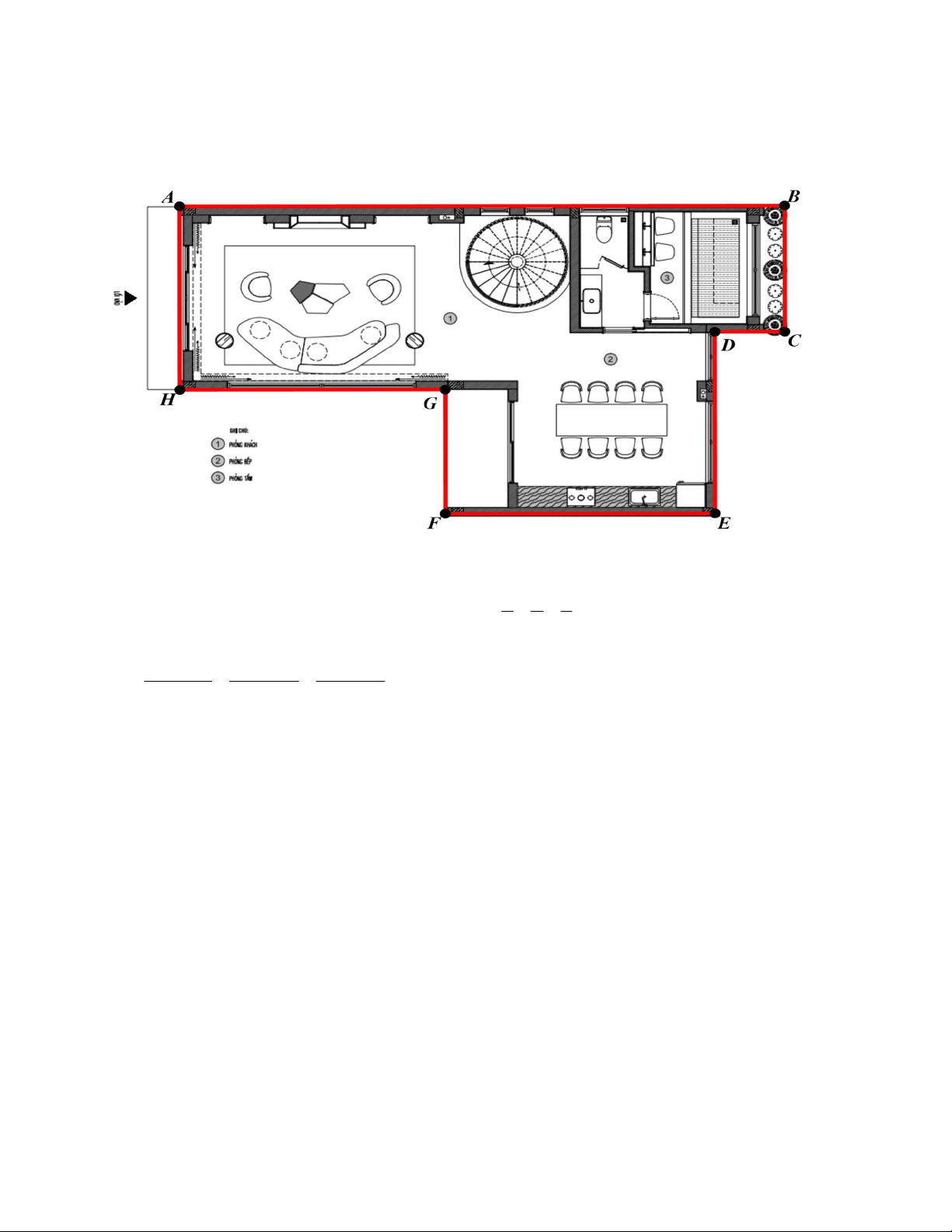
2)Cho hình vẽ dưới đây là bản thiết kế thi công tầng 1 của một ngôi nhà hai tầng mái bằng. Biết  ABC  BAH  AHG  HGF  GFE  FED  EDC  DCB 90         ; AB  6BC  18 ; m DE  6 ; m GF  4 ; m EF  7 ; m GH  DC  4 .
m Biết giá thiết kế mỗi mét vuông sàn là 120 nghìn đồng (mỗi
sàn là một tầng). Hỏi bác chủ nhà phải trả bao nhiêu tiền để mua bản thiết kế của cả ngôi nhà đó? Câu 5: (2,0 điểm) 1 1 1
1) Cho các số thực dương x, y, z thay đổi thỏa mãn    3 . Tìm giá trị nhỏ nhất của biểu thức x y z 2 x  z   2 1 y  x   2 1 z  y   1 P    . z  2 x   1 x  2 y   1 y  2 z   1
2) Thầy giáo viết lên bảng các số tự nhiên liên tiếp từ 1 đến 2024. Hai bạn học sinh thực hiện trò chơi như
sau: cứ một bạn thực hiện việc xóa đi hai số bất kỳ trên bảng thì bạn còn lại sẽ viết thay vào đó một số là
giá trị tuyệt đối của hiệu hai số vừa xóa. Trò chơi chỉ kết thúc khi trên bảng còn đúng một số. Hỏi số cuối
cùng trên bảng có thể là số 2023 được không? --------HẾT--------
Họ và tên thí sinh : …………………………………….. Số báo danh: …………………………………..
Họ, tên, chữ kí GT 1 : …………………………… Họ, tên, chữ kí GT 2 : ……………………………….