
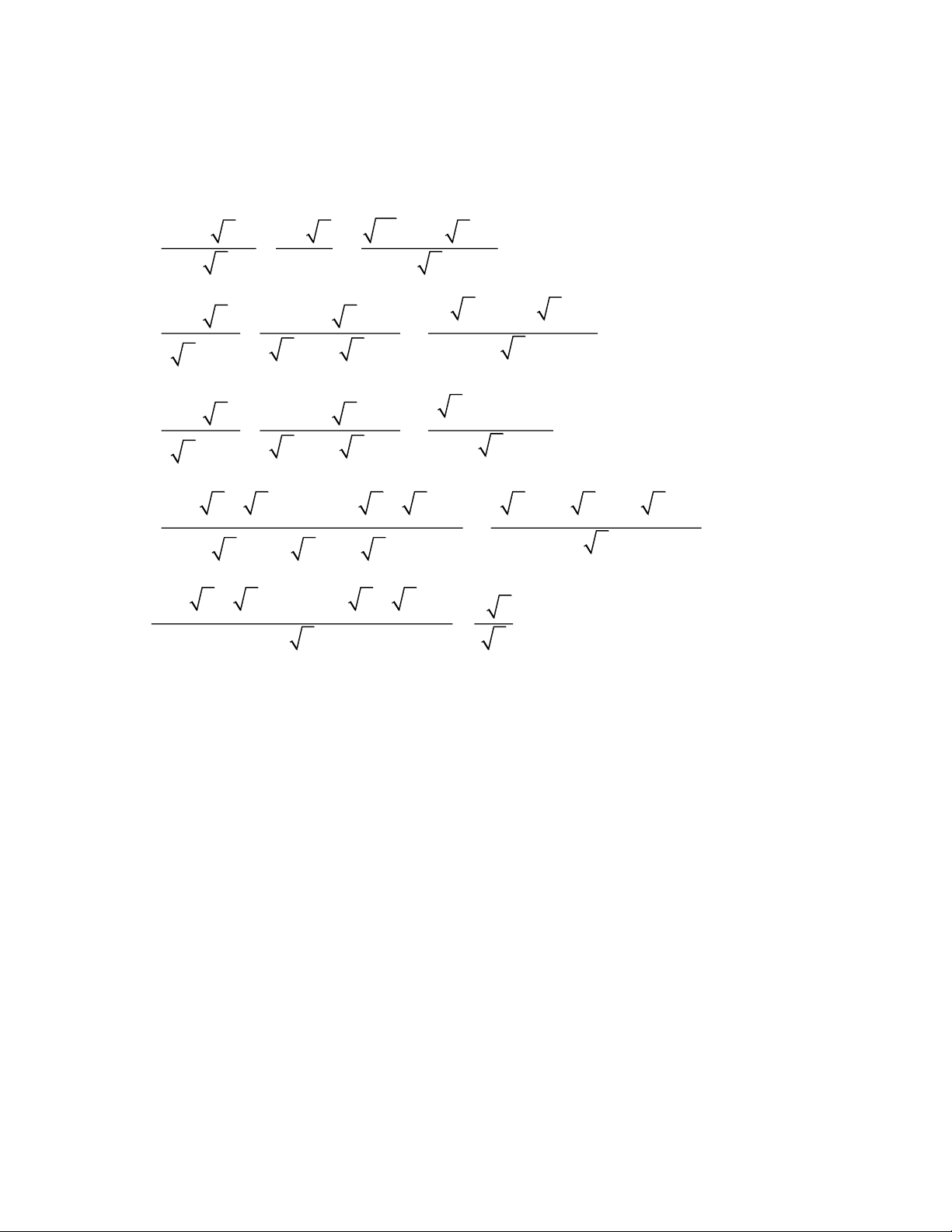



Preview text:
Đề thi khảo sát chất lượng đầu năm lớp 10 năm 2020 – 2021
Môn: Toán – Đề số 4 Thời gian: 90 phút
Câu 1: Chứng minh biểu thức sau không phụ thuộc vào x + − 3 2 x 2 x
x + x − x − 1 A = + . + + − x 2 x 1 x 1 x Câu 2:
1. Không sử dụng máy tính cầm tay giải phương trình và hệ phương trình sau: 2x + y = 7 b. 4 2
x − 6x + 8 = 0 a. x − 3y = 7
2. Tìm tham số m để hàm số y = (m − 2) x + 3m − 1 nghịch biến trên
Câu 3: Cho phương trình: 2 x − 2(m − )
1 x + m − 2 = 0
a. Giải phương trình với m = 1
b. Tìm m để phương trình có 2 nghiệm phân biệt x ,x thỏa mãn biểu thức: 1 2 2 2
x + x − x x = 4 1 2 1 2
Câu 4: Một người đi xe máy từ A đến B với vận tốc 40km/h. Khi đến B người đó
nghỉ 30 phút rồi quay về A với vận tốc 50km/h. Tính quãng đường AB biết tổng
thời gian người đó đi từ A đến B , từ B về A và thời gian nghỉ là 7 giờ 15 phút.
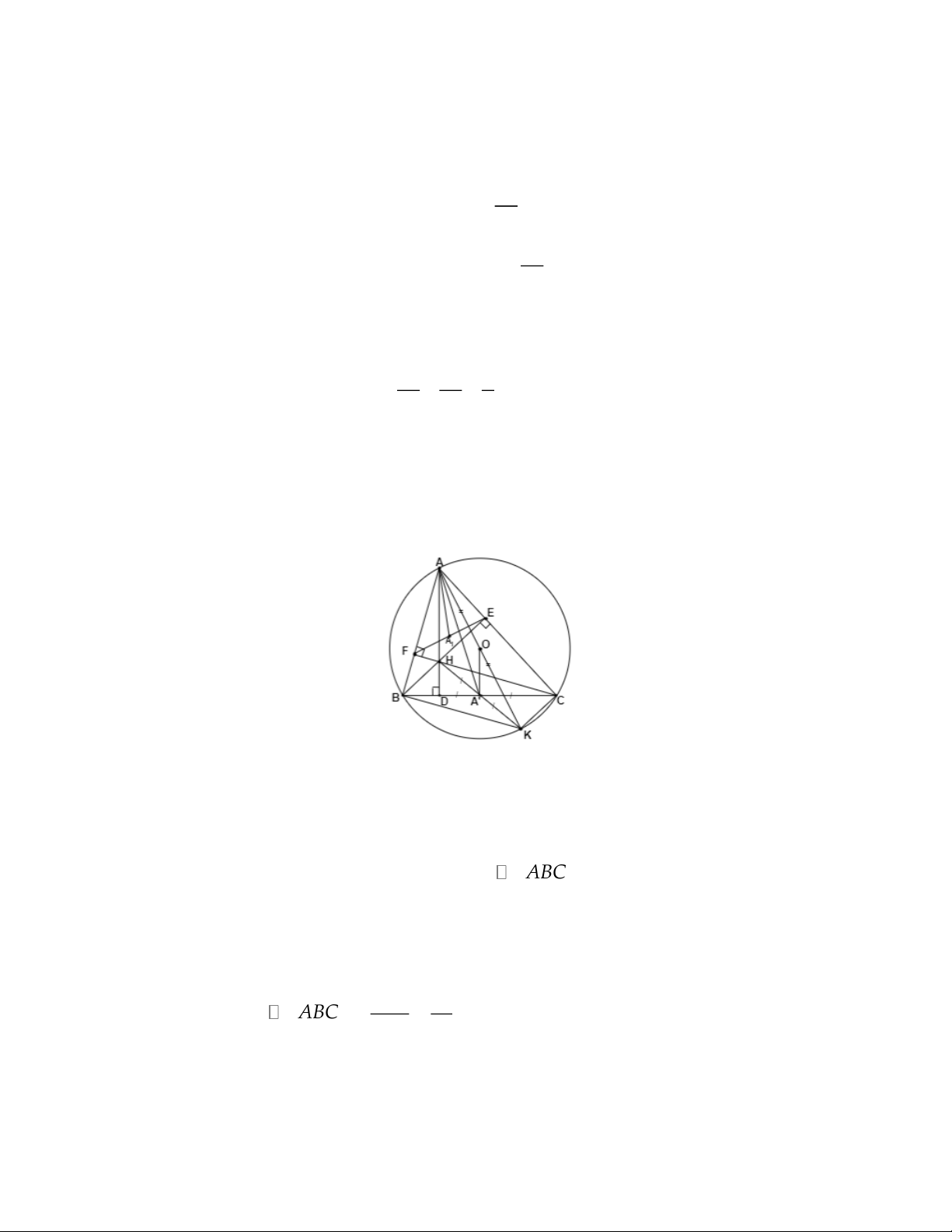
Câu 5: Cho đường tròn (O, R). BC là một dây cung (BC 2R ). Một điểm A di
động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC. Các đường cao
AD, CF, BE cắt nhau tại điểm H.
a. Chứng minh rằng: A EF A BC
b. Gọi A’ là trung điểm của BC. Chứng minh AH = 2OA'
c. Gọi A Là trung điểm của EF. Chứng minh rằng: RAA = OA'.AA' 1 1
d. Tìm vị trí của A để EF + FD + DE đạt giá trị lớn nhất 1 1 1
Câu 6: Cho x, y, z là những số thực dương và + + = 2 x + 1 y + 1 z + . Chứng 1 1 minh rằng: xyz 8
Đáp án Đề thi khảo sát chất lượng đầu năm năm 2020 – 2021 Đề số 4
Câu 1: Điều kiện xác định: x 0, x 1 + − 3 2 x 2 x
x + x − x − 1 A = + . + + − x 2 x 1 x 1 x x + − + + x − x
( x 1) ( x 1 2 2 ) A = ( + x ) . 2 ( x −1)( x + + 1 1 ) x + − 2 + x 2 − x
( x 1)(x 1) A = ( + x ) . 2 ( x −1)( x + + 1 1 ) x ( 2 x )( x 1) (2
x )( x 1) ( x 1)( x 1)( x 1) + − + − + + − + A = ( + 1) . 2 ( −1)( +1) x x x x
(2+ x)( x − )1+(2− x)( x + )1 2 x A = = = 2 = const x x Câu 2: 1. 2x + y = 7 2x + y = 7 2x + y = 7 x = 4 a. x − 3y = 7
2x − 6y = 14 7y = 7 − y = 1 −
Vậy hệ phương trình có nghiệm (x, y) = (4, 1 − ) b. 4 2
x − 6x + 8 = 0 Đặt 2
x = t,(t 0) phương trình trở thành: 2
t − 6t + 8 = 0 2
' = 3 − 8 = 1 ' = 1 0 x = 2 2
x = 4 x = 2 t 3 1 4 − = + = 1 t = 3 − 1 = 2 x = 2 2 2 x = 2 x = − 2
Vậy phương trình có 4 nghiệm x = 2 ,x = 2
b. Để hàm số nghịch biến trên R thì m − 2 0 m 2
vậy m < 2 thì hàm số nghịch biến trên R Câu 3:
a. Thay m = 1 vào phương trình ta có: x = 1 2 2
x − 1 = 0 x = 1 x = 1 −
b. Để phương trình có 2 nghiệm phân biệt ta có: ' 0 ' = (m − )2 2
1 − m + 2 = m − 3m + 3 0 −b x + x = = 2 m − 1 1 2 ( )
Áp dụng hệ thức Viet ta có: a c x .x = = m − 2 1 2 a Theo bài ra: 2 2
x + x − x x = 3 1 2 1 2
(x + x )2 − 3x x = 3 1 2 1 2 2
4(m − 1) − 3(m − 2) = 3 7 m = 2 4m 11m 7 0 − + = 4 (tm) m = 1 7 Vậy m =
hoặc m = 1thì phương trình có 2 nghiệm phân biệt x ,x thỏa mãn biểu 4 1 2 thức: 2 2
x + x − x x = 4 1 2 1 2 Câu 4:
Gọi quãng đường AB là x (km) x > 0 x
Thời gian lúc đi từ A đến B của xe máy là: (km/h) 40 x
Thời gian lúc đi về từ B đến A của xe máy là: (km/h) 50
Do tổng thời gian người đó đi từ A đến B, từ B về A và thời gian nghỉ là 7,25 giờ
Khi đó ta có phương trình: x x 1 + + = 7,25 40 50 2
Dễ dàng tìm được x = 150 km
Vậy quãng đường AB là 150 km Câu 5: Chứng minh
a. Tứ giác BFEC nội tiếp
AEF = ACB ( cùng bù BEF )
AEF = ABC ( cùng bù FEC ). Vậy A EF A BC
b. Kẻ đường kính AK nên ta có KB // CH, KC // BH
BHKC là hình bình hànhA’ là trung điểm của KH KO là đường trung
bình của tam giác AHK AH = 2AO AA' R c. Ta có: A EF A BC =
(1) R là bán kính đường tròn ngoại tiếp AA R' 1
tam giác ABC, R’ là bán kính đường tròn ngoại tiếp tam giác AEF, AA’ là
trung tuyến tam giác ABC, AA là trung tuyến tam giác AEF 1
Ta lại có AEHF nội tiếp đường tròn đường kính AH nên đây cũng là đường
tròn ngoại tiếp tam giác AEF AH 2OA' Từ (1) .
R AA = AA'.R' = AA'. = AA'. .
R AA = AA'.OA' 1 1 2 2
d. Gọi M, N lần lượt là trung điểm của AC, AB
Ta có: OM ⊥ AC,ON ⊥ AB OA’, OM, ON lần lượt là các đường cao của tam giác OBC, OCA, OAB 1 S = S + S + S =
OA BC + OM AC + ON AB (2) ABC OCA OCB OAB ( '. . . ) 2 2S
= OA'.BC + OM.AC + ON.AB ABC . R AA AA Ta có: 1 OA' =
(theo chứng minh câu c). Mà
1 là tỉ số 2 trung tuyến AA' AA' AA EF
của 2 tam giác đồng dạng AEF và ABC nên 1 = . Tương tự ta có: AA' BC . R FD . R DE OM = , ON = AC AB . R AA . R FD . R DE 1 2S = R .BC + .AC + .AB Thay vào (2) ta được: ABC AA' AC AB 2S
= R EF + FD + DE ABC ( )
Do R không đổi nên EF + FD + DE đạt giá trị lớn nhất khi diện tích tam giác ABC đạt max 1 Ta có S
= BC.AD do BC không đổi nên diện tích tam giác ABC lớn nhất ABC 2 khi AD lớn nhất
Mà AD lớn nhất khi A nằm chính giữa cung BC . Câu 6: Ta có: 1 1 1 1 1 = 2 − − = 1− + 1− x + 1 y + 1 z + 1 y + 1 z + 1 y z yz = + 2 y + 1 z + 1 (y +1)(z +1) 1 xz 1 xy Tương tự ta có: 2 y + (x+ )1(z+ ) , 2 1 1 z + 1 (x+ )1(y + )1
Nhân các vế của bất dẳng thức ta được điều phải chứng minh




