Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 năm học 2022 - 2023 - Đề số 3

Môn: Toán – Đề số 3 Thời gian: 90 phút
Câu 1: Cho biểu thức
 x x −1 x x +1 x − 2 P =  − .  x − x
x + x  x + 2  a. Rút gọn biểu thức.
b. Tìm giá trị của x nguyên để P đạt giá trị nguyên. Câu 2: 2 2
x + xy + y −1 = 0
a. Giải hệ phương trình: 
 x − y = 3 + xy b. Giải phương trình: 2 2
25 − x − 10 − x = 3
Câu 3: Cho phương trình: 2 x − (m − ) 2 2
1 x + m − 3m = 0
Tìm giá trị tham số m để phương trình có 2 nghiệm phân biệt cùng âm
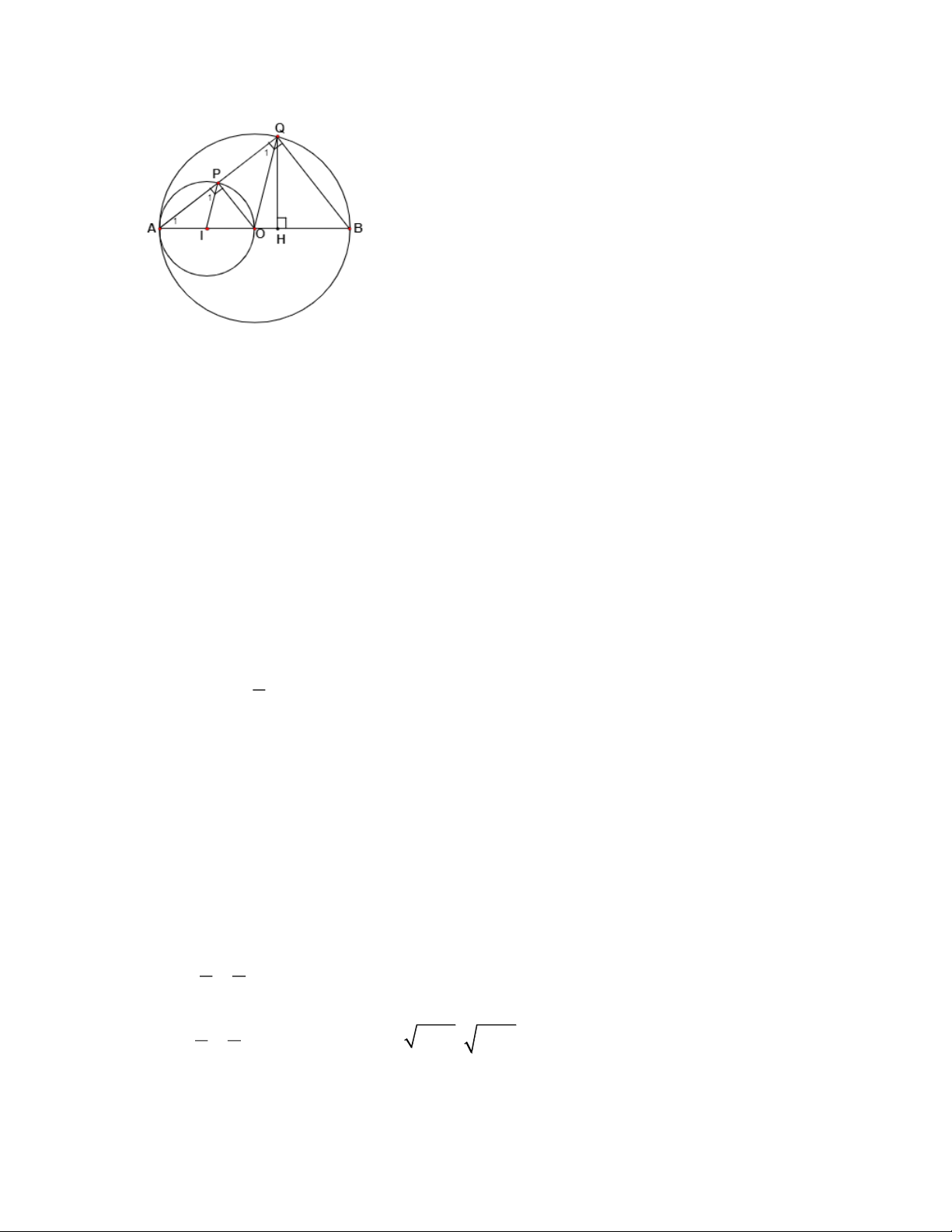
Câu 4: Cho đường tròn tâm O đường kính AB. I là trung điểm của OA. Đường
tròn tâm I đi qua A, P là điểm bất kì nằm trên đường tròn tâm I, AP cắ (O) tại Q
a. Chứng minh rằng (I), (O) tiếp xúc với nhau tại A
b. Chứng minh: IP / /OQ c. Chứng minh: PQ = PA
d. Xác định vị trí của P để tam giác ABQ có diện tích lớn nhất 1 1
Câu 5: Chứng minh rằng: x − 1 + y − 1 = x + y biết x  0, y  0, + = 1 x y Đáp án Đề số 3
Câu 1: Điện kiện: x  0, x  1, x  2, x  0
 x x −1 x x +1 x − 2 P =  − .  x − x
x + x  x + 2    − (  x + x )3 3 1 ( ) 1  x − 2 P = −   x ( x − ) x ( x +  ) .x+2 1 1   
( x 1)(x x 1) ( x 1)(x x 1) − + + + − + x −   2 P = −   x  ( x − ) x ( x +  ) .x+2 1 1 
(x x 1) (x x 1) + + − + x −   2 P = − .  x x  x + 2   2 x x − 2 2.(x − 2) P = . = x x + 2 x + 2 2 x − 2 8 b. P (x) ( ) = = 2 − x + 2 x + 2
Để P(x) nguyên thì x + 2U (8) =  1  , 2  , 4  ,   8 ta có bảng sau x +2 -8 -4 -2 -1 1 2 4 8 x -10 -6 -4 -3 -1 0 2 6
Kết hợp với điều kiện xác định ta có: x = 6 thỏa mãn
Vậy x = 6 thì P(x) đạt giá trị nguyên Câu 2: a.
x + xy + y −1 = 0 (x − y)2 2 2 = 1− 3xy   
 x − y = 3 + xy
 x − y = 3 + xy (3+ xy)2 2 2 = 1− 3xy
9 + 6xy + x y = 1− 3xy    
 x − y = 3 + xy 
x − y = 3 + xy 2 2
x y + 9xy + 8 = 0 (1)
  x−y = 3+xy (2)
Từ phương trình (1) ta đặt xy = t. Phương trình trở thành t = 1 − xy = 1 − 2
t + 9t + 8 = 0     t = 8 − xy = 8 − Với xy = 1
− kết hợp với phương trình (2) ta có :  xy = 1 − (y + 2).y = 1 − y = 1 −     
 (x, y) = (1,− ) 1 x − y = 2  x = y + 2  x =1
Với xy = 8 kết hợp với phương trình (2) ta có :
Vậy hệ phương trình có nghiệm  (x y) 11+ 3 17 1 − 1+ 3 17  11− 3 17 1 − 1− 3 17  , =  ,  =  ,      ( 2 2 2 2    
x, y ) = (1, − ) 1 11+ 3 17 1 − 1+ 3 17  11− 3 17 1 − 1− 3 17  =  ,  =  ,      2 2 2 2     b. 2 2
25 − x − 10 − x = 3 2 25− x  0  5 −  x  5 
Điều kiện xác định:   
 − 10  x  10 2 10  − x  0 
− 10  x  10 2
a = 25− x Đặt  ,(a,b  0) 2
b = 10 − x Phương trình trở thành:
 a − b = 3  a − b = 3 a − b = 3      2 2 a − b = 15 (   a − b 
)(a+b) = 15 a+b = 5  2 a = 4  25 − x = 4  x = 3 2      x = 9   (tm) = 2 b 1  − = x = 3  10 x 1 −  
Vậy phương trình có nghiệm x = 3 hoặc x = -3 Câu 3: 2 x − (m − ) 2 2
1 x + m − 3m = 0
Để phương trình có hai nghiệm âm phân biệt ta có:   '  0 (  m − )2 2
1 − m + 3m  0  m 1       1 m  3 2 x .x  0   m − 3m  0 0  m  3 1 2 Vây 1 Câu 4: Chứng minh
a. Ta có: OI = OA − IA  (O) và (I) tiếp xúc với nhau tại A
b. Tam giác OAQ cân tại O  Q = A 1 1
Tam giác IAP cân tại O  P = A 1 1
 Q = P  IP / /OQ 1 1 c. 0
APO = 90 (góc nội tiếp chắn nửa đường tròn)  OP ⊥ AQ  OP là đường
cao của tam giác OAQ mà OAQ cân tại O nên OP là đường trung tuyến  AP = PQ
d. Kẻ HQ vuông góc với AB. 1 Ta có: S = . AB QH ABQ 2
Mà AB là đường kính không đổi nên S
lớn nhất khi QH lớn nhất hay Q ABQ
trùng với trung điểm của AB
Muốn Q trùng với trung điểm của AB thì P là trung điểm của cung AO
Thật vậy P là trung điểm của cung AO thì PI ⊥ AO mà IP / /OQ  QO ⊥ AB tại O
Vậy Q là trung điểm của AB kéo theo H trùng với O, OQ lớn nhất neenn QH lớn nhất 1 1 Câu 5: + = 1 (1) x y 1 1 Ta có: +
= 1  x  1,y  1, x − 1, y − 1 x y
Từ (1) ta có: x + y = xy  xy − x − y + 1 = 1  (x − 1)(y − 1) = 0  (x − )
1 (y − 1) = 1  2 (x − 1)(y − 1) = 2
 x + y = x + y + 2 (x −1)(y −1) − 2 = ( x −1 + y −1)2
 x + y = x − 1 + y − 1