Đề thi khảo sát chất lượng Toán 10 năm học 2016 – 2017 trường THPT Thạch Thành 1 – Thanh Hóa lần 4

Đề thi khảo sát chất lượng Toán 10 năm học 2016 – 2017 trường THPT Thạch Thành 1 – Thanh Hóa lần 4 gồm 7 bài tập tự luận, có hướng dẫn giải và thang điểm, mời các bạn đón xem

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
TRƯỜNG THPT THẠCH THÀNH I
TỔ TOÁN- TIN
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN 4
MÔN TOÁN_KHỐI 10
Năm học: 2016- 2017
Thời
g
ian: 120 phút
Câu 1 (2 điểm): Cho hàm số:
2
4yx xc
a) Tìm
c
biết rằng đồ thị của hàm số là một parabol đi qua điểm
2; 1A
.
b) Vẽ đồ thị của hàm số ứng với giá trị
c
tìm được.
Câu 2 (2 điểm):
a) Giải bất phương trình:
543x ;
b) Giải phương trình:

2
44 6 2 3
x
xx x
.
Câu 3 (2 điểm):
a) Cho
5
sin cos
4
xx
. Tính giá trị của sin 2
x
.
b) Chứng minh trong mọi tam giác ABC ta đều có:
cot cot cot cot .cot .cot
222 222
A
BC ABC

Câu 4 (1 điểm):
Cho tam giác đều ABC cạnh a (
0a
). MNPQ là hình chữ nhật
nội tiếp tam giác ABC (như hình vẽ). Tính diện tích lớn nhất có
thể đạt được của hình chữ nhật MNPQ theo a.
A
B
C
M
N
Q
Câu 5 (1 điểm): Trong mặt phẳng tọa độ
Ox
y
, cho tam giác ABC có phương trình đường
thẳng chứa đường cao kẻ từ B là:
3180xy
, phương trình đường trung trực của đoạn
BC là:
3 19 279 0xy, đỉnh C thuộc đường thẳng :2 5 0dxy. Tìm tọa độ điểm A biết
rằng
0
135BAC .
Câu 6 (1 điểm): Tùy theo m tìm giá trị nhỏ nhất của biểu thức:

22
,4212 3Fxy x y x my (m là tham số)
Câu 7 (1 điểm): Giải hệ phương trình:
18)12()12(
)3(5132
22
22
yx
yxyx
----------Hết----------
ĐÁP ÁN TOÁN 10 LẦN 4
Câu Đá
p
án Đi
ểm
1.a.
3c
1
1.b.
10
8
6
4
2
2
4
15 10 5 5 10 15
3
3
1
2.a.

54955 1
:1;
x
B
PT x x x
KL T


1
2.b.
ĐK:
46x
Đặt
 
4 6 0 5txx t
Phương trình trở thành:
05
22
22
3
4214210 3
7
5
3 2 24 9 2 15 0
3
t
t
tt t t t
t
x
txx xx
x

 



0,5
0,5
3.a.

2
2
22
5
sin cos sin cos 2.sin .cos 1 sin 2
4
25 9
sin 2 1
16 16
x
xxxxx x
x





1
3.b.
Ta có:
cot .cot 1
1
22
cot tan
22
cot cot cot
22 2
cot .cot 1 cot cot cot
22 2 2 2
cot cot cot cot .cot .cot
222 222
AB
AB C
AB C
AB C A B
ABC ABC
dfcm









1
4.
Giả sử
; 0
A
Mx MNx xa 



max
0
2
2
2
3
.sin60
2
333
.
2228
3
82
MNPQ
MNPQ
MQ BM a x
xax
a
SMNMQxax
aa
Sxaxx






A
B
C
M
N
Q
1
5.
Giả sử

18 3 2 5
18 3 ; ; ;2 5 ;
22
bcb c
BbbCcc M





là trung điểm của BC.

18 3 2 5
3. 19. 279 0
9
22
4
.0
19 3 18 3 2 5 0
bc b c
M
c
b
BC u
cb cb






 
 

9; 23
6; 4
C
B
Gọi H là hình chiếu của B trên AC.
Phương trình AC:
3403;5xy H
Do
00
135 45BAC BAH HAB
vuông cân tại H.
10HA HB
 

22
2; 2
2
;3 4 ; 10 3 3 9 10
4
4;8
A
a
Aa a AH a a
a
A

Vì A nằm giữa H và C nên

4;8A
Vậy
4;8A
0,5
0,5
6.
Nhận xét
;0,Fx
y
x
y

Gọi
12
:4 2 1 0; :2 3 0dxy dxmy


00
11200
00
0
min
0
4410
:1 ;
230
;0
xy
TH m d d I x y
xmy
xx
Fxy
yy





22
212
:1 ;4212 3TH m d d F x y x y x y
Đặt :

22 2
2
2 ; 2 1 3 5 10 10 5 1 5 5txyt Ft t t t t t 
min
51210Ft xy (đạt tại nhữn điểm nằm trên đường thẳng 210xy )
KL:

min
min
1: ; 0
1: ; 5
mFxy
mFxy


0,5
0,5
7.
+ Đk:
03
01
02
22
yx
y
x
Từ (2) 4
22
yxyx
+ Thay vào (1) ta có
)1(5132 yxyx 622)1)(2(3 yxyx
)1(2)2(2)1)(2(3 yxyx
(*)
+ Nếu y = 1 2 x không thỏa mãn hệ nên y-1 0
Chia 2 vế pt (*) cho y - 1 ta có :
02
1
2
3
1
2
2
y
x
y
x
2
1
2
)(
2
1
1
2
y
x
loai
y
x
Với
642
1
2
yx
y
x
. Thay vào (2)
2
17
19
y
y
)/(,
2
17
26
mt
x
x
0,5
Vậy hệ có nghiệm là:

yx;
= (2; 2) ;

yx;
= (
17
19
;
17
26
)
0,5
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT THẠCH THÀNH I
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN 4 TỔ TOÁN- TIN MÔN TOÁN_KHỐI 10 Năm học: 2016- 2017 Thời gian: 120 phút
Câu 1 (2 điểm): Cho hàm số: 2
y x  4x c
a) Tìm c biết rằng đồ thị của hàm số là một parabol đi qua điểm A2;  1 .
b) Vẽ đồ thị của hàm số ứng với giá trị c tìm được.
Câu 2 (2 điểm):
a) Giải bất phương trình: 5x  4  3 ; b) Giải phương trình:
  x  x 2 4 4 6
x  2x  3 .
Câu 3 (2 điểm): a) Cho 5
sin x  cos x  . Tính giá trị của sin 2x . 4
b) Chứng minh trong mọi tam giác ABC ta đều có: A B C A B C cot  cot  cot  cot .cot .cot 2 2 2 2 2 2
Câu 4 (1 điểm):
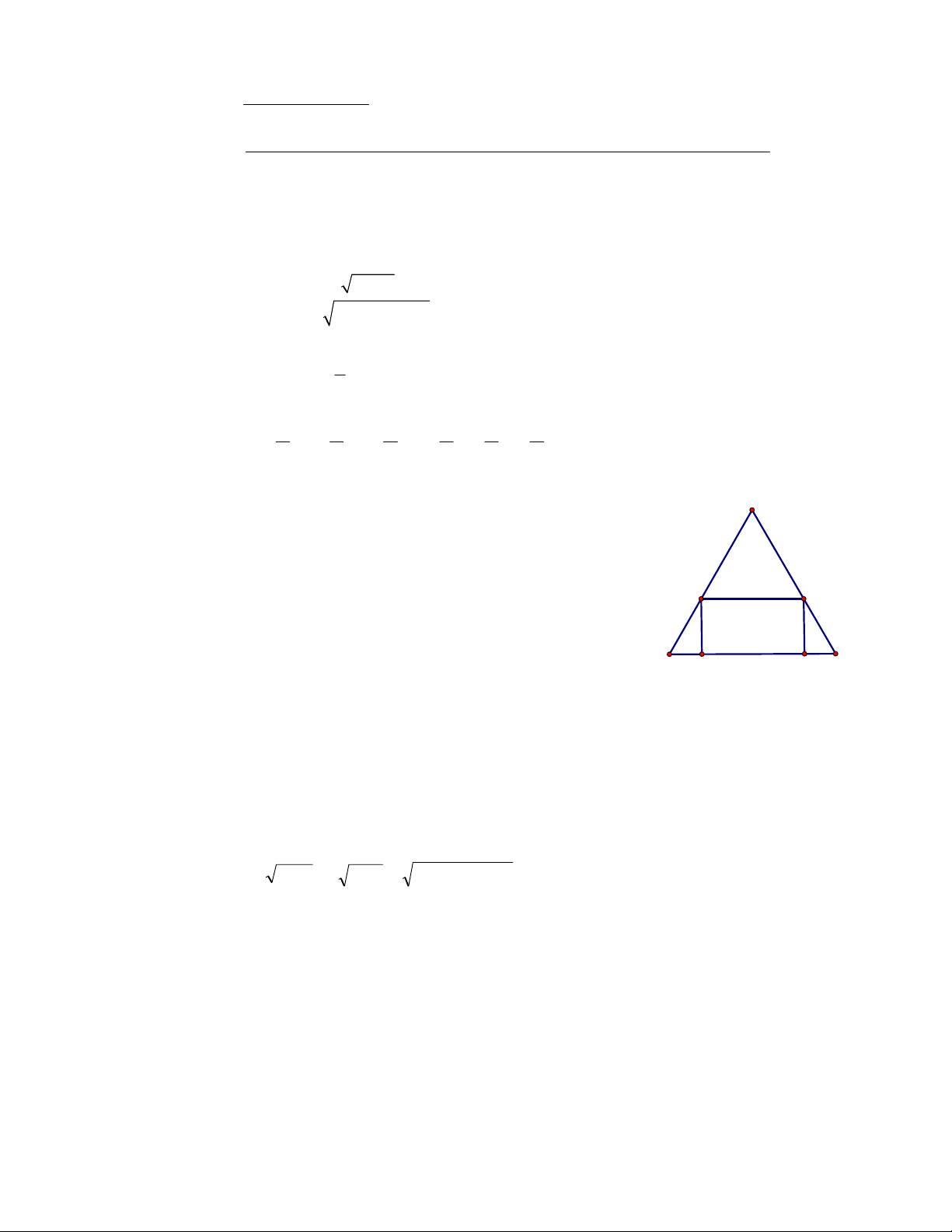
Cho tam giác đều ABC cạnh a ( a  0 ). MNPQ là hình chữ nhật A
nội tiếp tam giác ABC (như hình vẽ). Tính diện tích lớn nhất có
thể đạt được của hình chữ nhật MNPQ theo a. M N B C Q P
Câu 5 (1 điểm): Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có phương trình đường
thẳng chứa đường cao kẻ từ B là: x  3y 18  0 , phương trình đường trung trực của đoạn
BC là: 3x 19y  279  0 , đỉnh C thuộc đường thẳng d : 2x y  5  0 . Tìm tọa độ điểm A biết rằng  0 BAC  135 .
Câu 6 (1 điểm): Tùy theo m tìm giá trị nhỏ nhất của biểu thức:
F x y   x y  2   x my  2 , 4 2 1 2 3 (m là tham số)
Câu 7 (1 điểm): Giải hệ phương trình:
 x  2  3 y 1  ( 5 2 x  2 y  ) 3  (2x  ) 1 2  (2 y  ) 1 2  18 ----------Hết---------- ĐÁP ÁN TOÁN 10 LẦN 4 Câu Đáp án Điểm 1.a. c  3 1 1.b. 1 10 8 6 4 3 2 15 10 5 5 10 15 3 2 4 2.a.
BPT  5x  4  9  5x  5  x  1 1
KL :T  1; x  2.b. ĐK: 4   x  6
Đặt t  4  x6  x 0  t  5 Phương trình trở thành: t  3 0,5 2 2 0t5 4t t
  21  t  4t  21  0   t  3  t  7  x  5 2 2
t  3  x  2x  24  9  x  2x 15  0   x  3  0,5 3.a. 2  5  1   
sin x  cos x2 2 2
 sin x  cos x  2.sin .
x cos x  1 sin 2x  4  25 9  sin 2x  1  16 16 3.b. A B cot .cot 1  A B C 1 2 2 cot  tan      2  2 A B C cot  cot cot 2 2 2  A BC A B 1 Ta có:  cot .cot 1 cot  cot  cot    2 2  2 2 2 A B C A B C  cot  cot  cot  cot .cot .cot  dfcm 2 2 2 2 2 2 4.
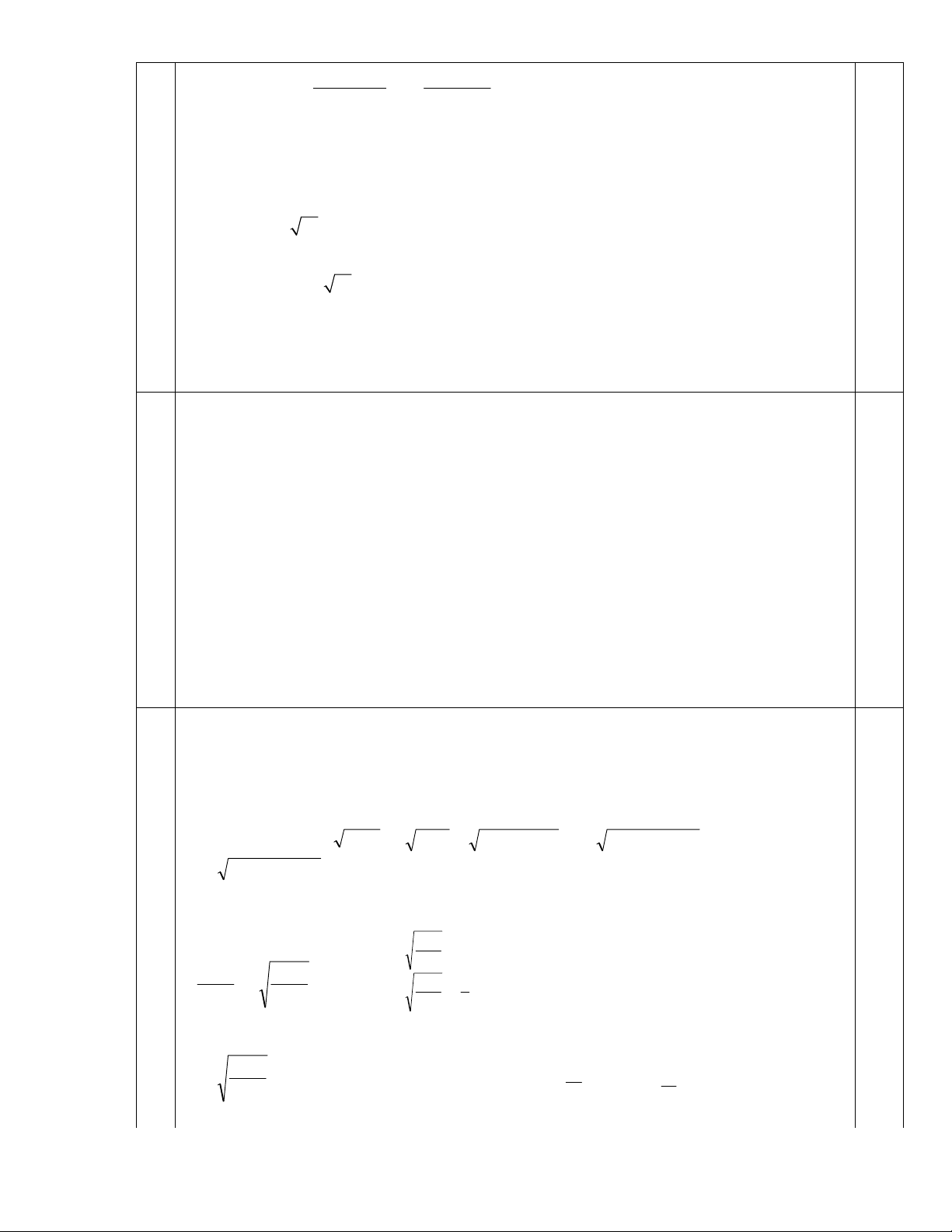
Giả sử AM x MN  ;
x 0  x a A 1 M N 3 0
MQ BM.sin 60  a x 2 2 2
x a x a B C S
MN MQ x a x     Q P MNPQ   3   3 3 . 2 2 2 8   2 a 3 a S
x a x x MN ma PQ x 8 2 5. 
b c b c   Giả sử B
b bC c c   18 3 2 5 18 3 ; ; ; 2 5  M ; 
 là trung điểm của BC.  2 2 
 18  3b c b  2c  5 M    3. 19.  279  0 c  9 C  9;23     2 2     BC.u  0   b  B  6;4  19
 c  3b 18  32c b  5 4  0 0,5
Gọi H là hình chiếu của B trên AC.
Phương trình AC: 3x y  4  0  H 3;5 Do  0  0
BAC  135  BAH  45  H
AB vuông cân tại H.
HA HB  10 a  2  A 2;2 2 2  
Aa;3a  4; AH  10  a  3  3a  9  10     a  4  A  4;8
Vì A nằm giữa H và C nên A4;8 0,5 Vậy A4;8 6. Nhận xét F  ; x y  0 x  , y
Gọi d : 4x  2 y 1  0; d : 2x my  3  0 1 2
x y  
TH : m  1  d d I x ; y  4 4 1 0 0 0  1 1 2 0 0
2x my 3  0  0 0   x x F x; y 0  0   min y y  0,5 0 TH : m  1
  d d F  ;
x y  4x  2y  2
1  2x y  32 2 1 2 2 2 2
Đặt : t x y t    F t   t    t   2 2 ; 2 1
3  5t 10t 10  5t   1  5  5
F  5  t  1
  2x y 1  0 (đạt tại nhữn điểm nằm trên đường thẳng 2x y 1  0 ) min m  1:  F  ; x y  0 KL: min 0,5 m  1:  F  ; x y  5 min 7. x  2  0  + Đk: y 1  0   2 x  2 y  3  0 Từ (2) 2 2
x y x y  4
+ Thay vào (1) ta có x  2  3 y 1  ( 5 x y  )
1  3 (x  2)( y  )
1  2x  2 y  6
 3 (x  2)( y  )
1  2(x  2)  2( y  ) 1 (*)
+ Nếu y = 1  x  2
 không thỏa mãn hệ nên y-1  0 0,5
Chia 2 vế pt (*) cho y - 1 ta có :  x22 y1 x  2 x   2  2 3  2  0  x2 1 y 1 y 1   (loai) y1 2  y2  x  2   x2   , (t / m) Với
 2  x  4y  6 . Thay vào (2) y 19 26 y 1   17 x  17  26 19 0,5
Vậy hệ có nghiệm là: x; y = (2; 2) ; x; y= ( ; ) 17 17