Đề thi khảo sát Toán 12 năm 2018 – 2019 trường THPT chuyên Bắc Ninh lần 2

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi khảo sát chất lượng theo định hướng thi tốt nghiệp THPT môn Toán 12 năm học 2018 – 2019.Mời bạn đọc đón xem.

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

39 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/6 - Mã đề thi 101
SỞ GD & ĐT TỈNH BẮC NINH
TRƯỜNG THPT CHUYÊN BẮC NINH
ĐỀ THI KHẢO SÁT LẦN 2 – NĂM HỌC 2018 - 2019
MÔN: TOÁN 12
Thời gian làm bài : 90 Phút (không kể thời gian giao đề)
(Đề có 50 câu trắc nghiệm)
(Đề có 05 trang)
Họ tên : ............................................................... Số báo danh : ...................
Câu 1: Giá tr lớn nht ca hm số
32
2 3 1y x x
trên đon
A.
1
;1
2
max 4.y
B.
1
;1
2
max 6.y
C.
1
;1
2
max 3.y
D.
1
;1
2
max 5.y
Câu 2: Xét các mệnh đề sau, mệnh đề no l mệnh đề đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song songvới nhau.
D. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau.
Câu 3: Một hình trụ có bán kính đáy
ra
, độ di đường sinh
2la
. Diện tích ton phần ca hình trụ
ny l:
A.
2
2 a
. B.
2
4 a
. C.
2
6 a
. D.
2
5 a
.
Câu 4: Có bao nhiêu phép tnh tiến biến một đường thẳng thnh chính nó?
A. 1 B. 2 C. Không có D. Vô số
Câu 5: Tập nghiệm ca bt phương trình
21
3 27
x
l:
A.
3; 
B.
1
;
3




C.
1
;
2




D.
2;
Câu 6: Trong các hm số dưới đây, hm số no nghch biến trên tập số thực ?
A.
1
2
logyx
. B.
3
x
y



. C.
2
x
y
e



. D.
2
4
log 2 1yx

.
Câu 7: Cho hm số
f
có đo hm trên khoảng
I
. Xét các mệnh đề sau:
(I). Nếu
0fx
,
xI
thì hm số nghch biến trên
I
.
(II). Nếu
0fx
,
xI
(du bằng chỉ xảy ra ti một số hữu hn điểm trên
I
) thì hm số nghch
biến trên
I
.
(III). Nếu
0fx
,
xI
thì hm số nghch biến trên khoảng
I
.
(IV). Nếu
0fx
,
xI
v
0fx
ti vô số điểm trên
I
thì hm số
f
không thể nghch biến
trên khoảng
I
.
Trong các mệnh đề trên. Mệnh đề no đúng, mệnh đề no sai?
A. I, II v IV đúng, còn III sai. B. I, II, III v IV đúng.
C. I v II đúng, còn III v IV sai. D. I, II v III đúng, còn IV sai.
Câu 8: Một nhóm có 10 người, cần chọn ra ban đi diện gồm 3 người. Số cách chọn l:
A.
240.
B.
3
10
.A
C.
3
10
.C
D.
360.
Câu 9: Trong mặt phẳng tọa độ
Oxy
cho bốn điểm
3; 5A
,
3;3B
,
1; 2C 
,
5; 10 .D
Hỏi
1
;3
3
G



l trọng tâm ca tam giác no dưới đây?
Mã đề 101
Trang 2/6 - Mã đề thi 101
A.
.ABC
B.
.BCD
C.
.ACD
D.
.ABD
Câu 10: Tập xác đnh ca hm số
1
5
1yx
l:
A.
0;
. B.
1; 
. C.
1; 
. D. .
Câu 11: Trong các hm số sau, hm số no l hm số chẵn.
A.
tanyx
B.
sinyx
C.
cosyx
D.
cotyx
Câu 12: Gọi
d
l tiếp tuyến ti điểm cực đi ca đồ th hm số
32
32y x x
. Mệnh đề no dưới đây
đúng?
A.
d
có hệ số góc dương. B.
d
song song với đường thẳng
3x
.
C.
d
có hệ số góc âm. D.
d
song song với đường thẳng
3y
.
Câu 13: Hình lập phương có my mặt phẳng đối xứng ?
A. 6 B. 8 C. 9 D. 7
Câu 14: Trong các dãy số sau, dãy no l cp số cộng:
A.
1
3.
n
n
u
B.
2
.
1
n
u
n
C.
2
1.
n
un
D.
52
.
3
n
n
u
Câu 15: Cho dãy số
1
1
5
( ):
n
nn
u
u
u u n

. Số 20 l số hng thứ my trong dãy?
A.
5.
B.
6.
C.
9.
D.
10.
Câu 16:
A
v
B
l hai điểm thuộc hai nhánh khác nhau ca đồ th hm số
2
x
y
x
. Khi đó độ di
đon
AB
ngắn nht bằng
A.
42
. B.
4
. C.
2
. D.
22
.
Câu 17: Cho hình lăng trụ đều
..ABC A B C
Biết mặt phẳng
()A BC
to với mặt phẳng
()ABC
một góc
30
v tam giác
A BC
có diện tích bằng
2
8.a
Tính thể tích khối lăng trụ
..ABC A B C
A.
3
8 3.a
B.
3
8.a
C.
3
83
.
3
a
D.
3
8
.
3
a
Câu 18: Cho hình chóp
S.ABCD
có đáy
ABCD
l hình bình hnh.
M
l một điểm thuộc đon
SB
(M
khác S v B). Mặt phẳng
ADM
cắt hình chóp
S.ABCD
theo thiết diện l
A. Hình bình hnh. B. Tam giác C. Hình chữ nhật. D. Hình thang.
Câu 19: Hm số no sau đây có đồ th như hình bên?
A.
42
43y x x
B.
42
23y x x
C.
2
2
21yx
D.
2
2
21yx
Câu 20: Tìm tập xác đnh ca hm số
2
1
log 5
y
x
A.
;5 \ 4 .
B.
5; .
C.
;5 .
D.
5; .
Trang 3/6 - Mã đề thi 101
Câu 21: Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện l một hình chữ nhật có diện
tích bằng
2
30cm
v chu vi bằng
26cm
. Biết chiều di ca hình chữ nhật lớn hơn đường kính mặt đáy ca
hình trụ (T). Diện tích ton phần ca (T) l:
A.
2
23 cm
. B.
2
23
2
cm
. C.
2
69
2
cm
. D.
2
69 cm
.
Câu 22: Cho
12
log 3 a
. Tính
24
log 18
theo
a
.
A.
31
3
a
a
. B.
31
3
a
a
. C.
31
3
a
a
. D.
31
3
a
a
.
Câu 23: Hệ số ca số hng chứa
6
x
trong khai triển nh thức
12
3
3
x
x



(với
0x
) l:
A.
220
.
729
B.
6
220
.
729
x
C.
6
220
.
729
x
D.
220
.
729
Câu 24: Khối nón
N
có bán kính đáy bằng
3
v diện tích xung quanh bằng
15
. Tính thể tích
V
ca
khối nón
N
A.
36V
B.
60V
C.
20V
D.
12V
Câu 25: Cho tứ diện
ABCD
có
,.AB AC DB DC
Khẳng đnh no sau đây l đúng?
A.
AB BC
B.
CD ABD
C.
BC AD
D.
()AB ABC
Câu 26: Cho phương trình
3
sin 2 - sin .
44
xx


Tính tổng các nghiệm thuộc khoảng
0;
ca
phương trình trên.
A.
7
.
2
B.
.
C.
3
.
2
D.
.
4
Câu 27: Hm số no trong bốn hm số được liệt kê dưới đây không có cực tr?
A.
23
2
x
y
x
. B.
4
yx
.
C.
3
y x x
. D.
2yx
.
Câu 28: Có bao nhiêu tiếp tuyến ca đồ th hm số
23
2
x
y
x
đi qua giao điểm hai đường tiệm cận?
A. 1. B. Không có. C. Vô số. D. 2.
Câu 29: Trong mặt phẳng tọa độ
Oxy
cho tam giác
ABC
có
3;4 , 6;1 , 7;3D E F
lần lượt l trung
điểm các cnh
, , .AB BC CA
Tính tổng tung độ ca ba đỉnh tam giác
.ABC
A.
16
3
B.
8
3
C.
8
D. 16
Câu 30: Cho hình chóp
.S ABC
có đáy ABC l tam giác vuông cân,
,BA BC a
90 ,SAB SCB
biết khoảng cách từ A đến mặt phẳng (SBC) bằng
3
2
a
. Góc giữa SC v mặt phẳng (ABC)l:
A.
.
6
B.
3
arccos .
4
C.
.
3
D.
.
4
Câu 31: Cho hm số có đồ th
C
. Có bao nhiêu điểm
A
thuộc
C
sao cho tiếp tuyến
ca
C
ti
A
cắt
C
ti hai điểm phân biệt
1 1 2 2
; , ;M x y N x y
(
,MN
khác
A
) thỏa mãn
1 2 1 2
5.y y x x
A.
1
. B.
2
. C.
0
. D.
3
.
Trang 4/6 - Mã đề thi 101
Câu 32: Giả sử đồ th hm số
2 4 2 2
( 1) 2 1y m x mx m
có 3 điểm cực tr l
,,A B C
m
A B c
xxx
. Khi quay tam giác ABC quanh cnh AC ta được một khối tròn xoay. Giá tr ca
m
để thể
tích ca khối tròn xoay đó lớn nht thuộc khoảng no trong các khoảng dưới đây:
A.
(4;6)
B.
2;4
C.
2;0
D.
(0;2)
Câu 33: Giải phương trình
8.cos2 .sin2 .cos4 2.x x x 
A.
32 4
.
3
32 4
xk
k
xk




B.
88
.
3
88
xk
k
xk




C.
32 4
.
5
32 4
xk
k
xk



D.
16 8
.
3
16 8
xk
k
xk




Câu 34: Tìm tt cả các giá tr thực ca tham số
m
để hm số
2
2
log 2
log 1
mx
y
xm

nghch biến trên
4;
.
A.
2m 
hoặc
1m
. B.
hoặc
1m
.
C.
2m 
hoặc
1m
. D.
2.m 
Câu 35: Đường cong ở hình bên l đồ th ca một trong bốn hm số dưới đây. Hm số đó l hm số no?
Câu 36: Cho hm số
32
( ) (2 1) (3 ) 2y f x x m x m x
. Tìm tt cả các giá tr ca tham số
m
để
hm số
()y f x
có 3 điểm cực tr.
A.
3.m
B.
3.m
C.
1
.
2
m
D.
1
3.
2
m

Câu 37: Có bao nhiêu số tự nhiên có 3 chữ số
abc
sao cho a, b, c l độ di 3 cnh ca một tam giác cân.
A. 45. B. 216. C. 81. D. 165.
Câu 38: Trong mặt phẳng tọa độ
,Ox y
cho tam giác
ABC
có
3;0 , 3;0AB
v
2;6 .C
Gọi
;H a b
l trực tâm ca tam giác
.ABC
Tính
6.ab
A. 10 B.
5
3
C. 60 D. 6
Câu 39: Một chiếc thùng đựng nước có hình ca một khối lập phương chứa đầy nước
.
Đặt vo trong
thùng đó một khối có dng nón sao cho đỉnh trùng với tâm một mặt ca lập phương, đáy khối nón tiếp
xúc với các cnh ca mặt đối diện. Tính tỉ số thể tích ca lượng nước tro ra ngoi v lượng nước còn li
ở trong thùng.
A.
2x 1
y
2x 1

B.
x1
y
x1

C.
x2
y
x1

D.
x
y
x1
Trang 5/6 - Mã đề thi 101
A.
.
12
B.
1
.
11
C.
.
12
D.
11
12
Câu 40: Cho giới hn
3
1 5 1
lim
43
x
x x a
b
xx

(phân số tối giản). Giá tr ca
2T a b
l:
A.
1
.
9
B. -1. C. 10. D.
9
.
8
Câu 41: Cho tứ diện
.ABCD
Gọi K, L lần lượt l trung điểm ca AB v
,BC
N l điểm thuộc đon CD
sao cho
2.CN ND
Gọi P l giao điểm ca AD với mặt phẳng
.KLN
Tính tỷ số
.
PA
PD
A.
1
.
2
PA
PD
B.
2
.
3
PA
PD
C.
3
.
2
PA
PD
D.
2.
PA
PD
Câu 42: Tìm số nghiệm ca phương trình
22
log x log x 1 2.
A.
0
B.
1
C.
3
D.
2
Câu 43: Hm số
2
y ln x mx 1
xác đnh với mọi giá tr ca x khi
A.
m2
m2

B.
m2
C.
2 m 2
D.
m2
Câu 44: Trong một lớp có
23n
học sinh gồm An, Bình, Chi cùng
2n
học sinh khác
.
Khi xếp tùy ý
các học sinh ny vo dãy ghế được đánh số từ 1 đến
23n
, mỗi học sinh ngồi một ghế thì xác xut để
số ghế ca An, Bình, Chi theo thứ tự lập thnh cp số cộng l
17
1155
.
Số học sinh ca lớp l:
A.
27.
B.
25.
C.
45.
D.
35.
Câu 45: Cho một khối lập phương có cnh bằng
.a
Tính theo a thể tích ca khối bát diện đều có các
đỉnh l tâm các mặt ca khối lập phương.
A.
3
4
a
B.
3
6
a
C.
3
12
a
D.
3
8
a
Câu 46: Đồ th hm số
y f x
đối xứng với đồ th ca hm số
( 0, 1)
x
y a a a
qua điểm
1;1I
.
Giá tr ca biểu thức
1
2 log
2018
a
f



bằng
A.
2016
. B.
2016
. C.
2020
. D.
2020
.
Câu 47: Tìm tt cả các giá tr thực ca tham số
m
để hm số
32
sin 3cos sin 1y x x m x
đồng biến
trên đon
3
;
2



.
A.
3m 
. B.
0m
. C.
3m 
. D.
0m
.
Câu 48: Một cái phễu có dng hình nón chiều cao ca phễu l
30 .cm
Người ta đổ một lượng nước vo
phễu sao cho chiều cao ca cột nước trong phễu bằng
15 .cm
(Hình
1
H
). Nếu bt kín miệng phễu rồi lật
ngược phễu lên (hình
2
H
) thì chiều cao ca cột nước trong phễu gần bằng với giá tr no sau đây?
Trang 6/6 - Mã đề thi 101
A. 1,553 (cm). B. 1,306 (cm). C. 1,233 (cm). D. 15 (cm).
Câu 49: Hm số
xx
2
y log 4 2 m
có tập xác đnh l thì
A.
1
m
4
B.
m0
C.
1
m
4
D.
1
m
4
Câu 50: Cho hình thang vuông
ABCD
với đường cao
2,AB a
các cnh đáy
AD a
v
3.BC a
Gọi
M
l điểm trên đon
AC
sao cho
.AM k AC
Tìm
k
để
.BM CD
A.
4
.
9
B.
3
.
7
C.
1
.
3
D.
2
.
5
----------- HẾT ----------
2
H
1
H
CÂU MÃ 101 MÃ 102 MÃ 103 MÃ 104 MÃ 105 MÃ 106 MÃ 107 MÃ 108
1 A D C B D D A B
2 C D C B B C D C
3 C C D D B B C D
4 D D D A D B A A
5 D A B C C C B A
6 C B C A A A B A
7 C A C C B A D A
8 C A C D D A D D
9 B D A B D A D A
10 C A C D C D C C
11 C B D B C C C A
12 D D C C D A C C
13 C C B B B C D D
14 D C D A A C A B
15 B B A A D A B B
16 B B A A A C A B
17 A A A A A A B B
18 D C D C B B C C
19 C C D D C B C C
20 A A B B B B C B
21 C D C C C C C A
22 B B D D D D B D
23 A A A A C D A C
24 D D C C B B B B
25 C C C B C C B D
26 B B D B B B A C
27 A A B D A C D B
28 B D A C D B C C
29 C C A B B D D B
30 C C C C C C B B
31 B B A B C C C C
32 B B A A C C D D
33 C C A A D D A A
34 D D D D D A B A
35 B B D A B D C C
36 A A A A A A C D
37 D A A A A A D D
38 A A A A D D C C
39 A B D D D D C A
40 C C D D C C A A
41 D D C C C D D D
42 B D C C D D A A
43 C C A A A A D B
44 D B C C B A C C
45 B A A D B B D D
46 B C B B B B D C
47 B B D D B B C C
48 B B C B D C C B
49 D D B A C B A D
50 D D D D D D C C
ĐÁP ÁN CÁC MÃ ĐỀ THI THỬ LẦN 2 KHỐI 12 (2018-2019)- MÔN TOÁN
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 1 Mã đề 101
Câu 1. Giá trị lớn nhất của hàm số trên đoạn .
3 2
2 3 1y x x
1
;1
2
A. . B. . C. . D. .
1
;1
2
max 4y
1
;1
2
max 6y
1
;1
2
max 3y
1
;1
2
max 5y
Lời giải
Tác giả: Bùi Nguyên Phương. Facebook: Bùi Nguyên Phương
Chọn A
Tập xác định: .
D !
Hàm số liên tục và có đạo hàm trên đoạn .
3 2
2 3 1y x x
1
;1
2
Đạo hàm: .
2
6 6y x x
Xét .
2
1
0 ;1
2
0 6 6 0
1
1 ;1
2
x
y x x
x
Ta có: ; ; .
1 1
2 2
y
0 1y
1 4y
Vậy .
1
;1
2
max 4y
lethuhang2712@gmail.com
Câu 2. Xét các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau .
GIẢI C.TIẾT ĐỀ THI THỬ THPTQG CHUYÊN BẮC NINH LẦN 2-2018-2019
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 2 Mã đề 101
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau.
Lời giải
Tác giả : Lê Thị Thu Hằng, FB: Lê Hằng
Chọn C
D
1
C
1
B
1
A
1
D
C
B
A
“Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau” và mệnh đề “Hai
mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau” là mệnh đề
sai, ví dụ trong hình lập phương trên ta có và cùng vuông góc với
1 1
( )C B BC
1 1
D B BD
nhưng 2 mặt phẳng đó lại cắt nhau.
( )ABCD
“Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau” là
mệnh đề sai ví dụ như trong hình lập phương trên ta có và cùng vuông góc với
1 1
A B
1 1
C B
1
B B
nhưng
1 1 1 1
A B C B
“Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau” là
mệnh đề đúng .
Tuandel2009@gmail.com
Câu 3. Một hình trụ có bán kính đáy r=a,độ dài đường sinh l=2a.Diện tích toàn phần của hình trụ này
là:
A. . B. . C. . D. .
2
2 a
2
4 a
2
6 a
2
5 a
Lời giải
Tác giả : Trần Minh Tuấn
Chọn C
,chọn C
2 2
2 2 2 .2 6
tp d xq
S S S a a a a
huonghieptb@gmail.com
Câu 4. Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó
A.1. B. 2. C. Không có. D. Vô số.
Lời giải
Họ và tên tác giả : Đào Thị Hương, FB: Hương Đào
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 3 Mã đề 101
Chọn D
Có vô số phép tịnh tiến biến một đường thẳng thành chính nó. Đó là các phép tịnh tiến có véc
tơ tịnh tiến là véc tơ không hoặc véc tơ tịnh tiến là véc tơ chỉ phương của đường thẳng đó.
Nguyendac1080@gmail.com
Câu 5. Tập nghiệm của bất phương trình 3
2x-1
>27 là:
A. . B. . C. . D. .
(3; )
1
( ; )
3

1
( ; )
2

(2; )
Lời giải
Tác giả :Nguyễn Văn Đắc, FB: Đắc Nguyễn
Chọn D
3
2x-1
>27
2 1 3
3 3 2 1 3 2
x
x x
Vậy tập nghiệm của bất phương trình là
(2; )
locleduc10@gmail.com
Câu 6. Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực .
! ?
A. . B. C. . D. .
1
2
logy x
3
x
y
2
x
y
e
2
4
log 2 1y x
Lời giải
Tác giả :Lê Đức Lộc, FB: Lê Đức Lộc
Chọn C
Hàm số là hàm số mũ, có cơ số nên hàm sốnghịch biến trên tập số thực
2
x
y
e
2
0 1a
e
.
R
nongdansanhdieu.tk@gmail.com
Câu 7. Cho hàm số có đạo hàm trên khoảng . Xét các mệnh đề sau:
f
I
(I). Nếu thì hàm số nghịch biến trên .
' 0,f x x I
I
(II). Nếu (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên ) thì hàm số
' 0,f x x I
I
nghịch biến trên .
I
(III). Nếu thì hàm số nghịch biến trên khoảng .
' 0,f x x I
I
(IV). Nếu và tại vô số điểm trên thì hàm số không thể nghịch biến
' 0,f x x I
' 0f x
I
trên khoảng .
I
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
A. II và IV đúng, còn III sai. B. I,II,III và IV đúng.
C.I và II đúng, còn III và IV sai. D.I,II và III đúng, còn IV sai.
Lời giải
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 4 Mã đề 101
Tác giả : Nguyễn Tuấn Đạt, FB: Nguyễn Đạt
Chọn C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng
I
hientam112@gmail.com
Câu 8. Một nhóm có 10 người, cần chọn ra ban đại diện gồm 3 người. Số cách chọn là:
A.
B.
C.
D.
240.
3
10
.A
3
10
.C
360.
Lời giải
Họ và tên: Bùi Thị Thu Hiền- Fb Hiền Tấm
Chọn C
+ Số cách chọn ra 3 người vào ban đại diện trong 10 người là: (không phân biệt thứ tự).
3
10
C
Chọn C
Quachthuy.tranphu@gmail.com.
Câu 9. Trong mặt phẳng tọa độ cho bốn điểm Hỏi
Oxy
A 3;-5 ,B -3;3 ,C -1;-2 ,D 5;-10 .
là trọng tâm của tam giác nào dưới đây?
1
;-3
3
G
A. . B. . C. . D. .
ABC
BCD
ACD
ABD
Lờigiải
Tácgiả:Quách Phương Thúy,FB:Phương Thúy
Chọn B
Ta thấy nên chúng không cùng phương là 3 đỉnh của
2; 5 , 8; 13BC BD
, ,B C D
một tam giác.
Mặt khác, ta lại có
3 1 5 1
3 3 3
3 2 10
3
3 3
B C D
B C D
x x x
y y y
Vậy là trọng tâm của tam giác
1
; 3
3
G
BCD
xuantoan204@gmail.com
Câu 10. Tập xác định của hàm số là:
1
5
1y x
A. . B. . C. . D. .
0;
1;
1;
!
Lời giải
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 5 Mã đề 101
Tác giả : Bùi Xuân Toàn, FB: Toan Bui
Chọn C
Phương pháp: Hàm số với không nguyên xác định khi .
y x
0x
Điều kiện xác định của hàm số là hay .
1
5
1y x
1 0x
1x
Vậy tập xác định: .
1;D 
hanhnguyentracnghiemonline@gmail.com
Câu 11. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. . B. . C. . D. .
tany x=
siny x=
cosy x=
coty x=
Lời giải
Tác giả : Nguyễn Thị Ngọc Hạnh, FB: Nguyễn Hạnh
Chọn C
Hàm số
là các hàm số lẻ.
tan , sin , coty x y x y x= = =
Hàm số
là hàm số chẵn
cosy x=
Mar.nang@gmail.com
Câu 12. Gọi là tiếp tuyến tại điểm cực đại của đồ thị hàm số . Mệnh đề nào dưới đây
d
3 2
3 2y x x
đúng
A. có hệ số góc dương. B. song song với đường thẳng .
d
d
3x
C. có hệ số góc âm. D. song song với đường thẳng .
d
d
3y
Lời giải
Tác giả : Lê Đình Năng, FB: Lê Năng
Chọn D
Ta có: .
2
' 3 6y x x
0 2
' 0
2 2
x y
y
x y
Bảng biến thiên
Từ bảng biến thiên ta suy ra đồ thị hàm số có điểm cực đại là
0;2
Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm là
0;2
0 0 2 2y x y
d
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 6 Mã đề 101
Do đó song song với đường thẳng
d
3.y
Trắc nghiệm: Hàm số đã cho có đạo hàm tại mọi điểm và tại điểm cực trị có nên tiếp
' 0y
tuyến của đồ thị hàm số tại điểm cực đại (hoặc tại điểm cực tiểu) là đường thẳng song song
d
trục hoặc trùng từ đó Chọn D.
,Ox
duyphuongdng@gmail.com
Câu 13. Hình lập phương có mấy mặt đối xứng?
A. 5. B. 6. C. 9. D. 10.
Lời giải
Tác giả: Đinh Thị Duy Phương, FB: Đinh Thị Duy Phương
Chọn D
Nguyenvandieupt@gmail.com
Câu 14. Trong các dãy số sau, dãy nào
là cấp số cộng:
A. . B. . C. . D. .
1
3
n
n
u
2
1
n
u
n
2
1
n
u n
5 2
3
n
n
u
Lời giải
Tác giả: Nguyễn Văn Diệu, FB:dieuptnguyen
Chọn D
Ta có dãy là cấp số cộng khi với là hằng số.
n
u
*
1
, n
n n
u u d
!
d
Bằng cách tính số hạng đầu của các dãy số ta dự đoán đáp án D.
3
Xét hiệu .
*
1
5 1 2
5 2 5
, n
3 3 3
n n
n
n
u u
!
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 7 Mã đề 101
Vậy dãy là cấp số cộng.
5 2
3
n
n
u
(nguyenthithutrang215@gmail.com)
Câu 15. Cho dãy số . Số là số hạng thứ mấy trong dãy?
1
1
5
:
n
n n
u
u
u u n
20
A. . B. . C. . D. .
5
6
9
10
Lời giải
Tác giả: Nguyễn Thị Thu Trang, FB: Trang Nguyễn
Chọn B
Cách 1:
1 2 3 4 5 6
5, 6, 8, 11, 15, 20u u u u u u
Vậy số là số hạng thứ .
20
6
Cách 2:
Dựa vào công thức truy hồi ta có
1
2
3
4
5
5 1
5 1 2
5 1 2 3
.....
1
5 1 2 ... 1 5
2
n
u
u
u
u
n n
u n
1
20 5 *
2
n n
n
!
2
6
30 0
5(lo¹ i)
n
n n
n
Vậy là số hạng thứ .
20
6
Cách 3: Sử dụng máy tính CASIO fx – 570VN PLUS
1 SHIFT STO A
5 SHIFT STO B
Ghi vào màn hình C = B + A: A = A + 1: B = C
Ấn CALC và lặp lại phím =
Ta tìm được số 20 là số hạng thứ 6
thuyhung8587@gmail.com
Câu 16. và
là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số . Khi đó độ dài đoạn
A
B
2
x
y
x
ngắn nhất bằng
AB
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 8 Mã đề 101
A. . B. . C. . D. .
4 2
4
2 2
2 2
Lời giải
Tác giả: Cấn Việt Hưng, FB: Viet Hung
Chọn B
x
y
2
1
O
1
Hàm số có đồ thị như hình vẽ. Gọi và là hai điểm
2
x
y
x
C
;
2
a
A a
a
;
2
b
B b
b
thuộc hai nhánh của .
C
2a b
Ta có: .
; ;
2 2 2 2
b a b a
AB b a b a
b a b a
Áp dụng BĐT Côsi ta có: .
2
2 2
4
b a
b a
Suy ra:
2
2
2
2
2 2
b a
AB b a
b a
2
2
64
16b a
b a
. Dấu bằng xảy ra khi và chỉ khi và .
4AB
2 2a
2 2b
Vậy .
min
4AB
(chamtt.toan@gmail.com)
Câu 17. Cho hình lăng trụ đều . Biết mặt phẳng tạo với mặt phẳng một
. ' ' 'ABC A B C
'A BC
ABC
góc và tam giác có diện tích bằng . Tính thể tích khối lăng trụ
0
30
'A BC
2
8a
. ' ' '.ABC A B C
A. . B. . C. . D. .
3
8 3a
3
8a
3
8 3
3
a
3
8
3
a
Lời giải
Tác giả :Trần Thị Chăm - HHA, FB: Cham Tran
Chọn A
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 9 Mã đề 101
Gọi là trung điểm của .
M
BC
Chứng minh được . Do đó góc giữa hai mặt phẳng và mặt phẳng
'BC AA M
'A BC
là góc .
ABC
!
0
' 30A MA
Đặt
AB x
Cách 1:
Tam giác đều nên
ABC
0
3
'
2 cos30
x AM
AM A M x
2 2 2
'
1 1
. ' . 8 4 4 3
2 2
A BC ABC
S A M BC x a x a S a
0
'
sin 30 ' 2
'
AA
AA a
A M
Vậy
3
. ' ' '.
'. 8 3
ABC A B C ABC
V AA S a
Cách 2:
Tam giác là hình chiếu của tam giác lên mặt phẳng
ABC
'A BC
0 2
'
.cos30 4 3
ABC A BC
ABC S S a
4 2 3x a AM a
0
'
tan30 ' 2
AA
AA a
AM
3
. ' ' '.
'. 8 3
ABC A B C ABC
V AA S a
thinhvanlamha@gmail.com
Câu18. Cho hìnhchóp có đáy là hình bình hành. là một điểm thuộc đoạn ( khác và ). Mặtphẳng cắt hình
.S ABCD
ABCD
M
SB
M
S
B
ADM
chóp theo thiết diện là
.S ABCD
A.Hình bình hành. B.Tam giác. C.Hình chữ nhật. D.Hình thang.
Lờigiải
Tácgiả :NguyễnVănThịnh, FB: ThịnhNguyễnVăn
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 10 Mã đề 101
Chọn D
Ta có là một điểm thuộc đoạn với khác và .
M
SB
M
S
B
Suy ra .
//
M ADM SBC
AD ADM
BC SBC
AD BC
// //ADM SBC Mx BC AD
Gọi thì cắt hình chóp theo thiết diện là tứ giác . Vì
N Mx SC
ADM
.S ABCD
AMND
và với không bằng nhau nên tứ giác là hình thang.
//MN AD
MN
AD
AMND
nhuthanh3112@gmail.com
Câu 19. Hàm số nào sau đây có đồ thị như hình bên?
A. . B. .
4 2
4 3
y x x
4 2
2 3
y x x
C. . D. .
2
2
2 1
y x
2
2
2 1
y x
Lời giải
Tác giả : Trần Như Thanh Nhã, FB: Nhã Trần Như Thanh
Chọn C
Dựa vào hình dạng của đồ thị hàm số suy ra hệ số a > 0 loại A, B.
4 2
y ax bx c
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 11 Mã đề 101
Và hàm số có 3 điểm cực trị a.b < 0
2
2
2 1
y x
kimoanh0102@gmail.com
Câu 20. Tìm tập xác định của hàm số .
2
1
log 5
y
x
A. . B. . C. . D. .
;5 \ 4
5;
;5
5;

Lời giải
Tác giả :Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh
Chọn A
Điều kiện xác định của hàm số là
.
2
5 0
5 5
log 5 0
5 1 4
x
x x
x
x x
Vậy tập xác định của hàm số là .
;5 \ 4
D

Hungvn1985@gmail.com
Câu 21. Cắt hình trụ bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện
T
tích bằng và chu vi bằng . Biết chiều dài của hình chữ nhật lớn hơn đường kính
30
2
cm
26 cm
mặt đáy của hình trụ . Diện tích toàn phần của là:
T
T
A. . B. . C. . D. .
23
2
cm
2
23
2
cm
2
69
2
cm
2
69 cm
Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn C
Gọi lần lượt là đường cao và bán kính đáy của hình trụ . Thiết diện của mặt phẳng và
,h r
T
hình trụ là hình chữ nhật . Khi đó theo giả thiết ta có
T
ABCD
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 12 Mã đề 101
2
2 2 2 2
.2 30 15 13 2 13 2
2 13
2( 2 ) 26
5 3( )
2 15 15 0
3
10( )
2
ABCD
ABCD
h r h r h r h r
S h r hr h r h r
h r
C h r
r h l
r r
r h TM
Vậy .
ngoquoctuanspt@gmail.com
Câu 22. Cho . Tính theo .
12
log 3 a
24
log 18
a
A. . B. . C. . D. .
3 1
3
a
a
3 1
3
a
a
3 1
3
a
a
3 1
3
a
a
Lời giải
Tác giả : Ngô Quốc Tuấn, FB: Quốc Tuấn
Chọn B
Ta có: .
12
log 3a
2
2
log 3
log 12
2
2
2
log 3
log 2 .3
2
2
2 2
log 3
log 2 log 3
2
2
log 3
2 log 3
2
2
log 3
1
a
a
Ta có: .
2
24
2
log 18
log 18
log 24
2
2
3
2
log 2.3
log 2 .3
2
2
1 2log 3
3 log 3
2
1 2.
1
2
3
1
a
a
a
a
3 1
3
a
a
Vậy .
24
log 18
3 1
3
a
a
Thuylinh133c3@gmail.com
Câu 23. Hệ số của số hạng chứa trong khai triển nhị thức (với ) là :
6
x
12
3
3
x
x
0x
A. . B. . C. . D. .
220
729
6
220
729
x
6
220
729
x
220
729
Lời giải
Tác giả : Nguyễn Thùy Linh, FB: Nguyễn Thùy Linh
Chọn A
Số hạng tổng quát trong khai triển là:
12
3
3
x
x
12
12 2 2 12
12 12
3
1 3 , 12 .
3
k k
k
k k k k
x
T C C x k k
x
!
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 13 Mã đề 101
chứa
T
6
x
2 12 6 9.k k
Vậy hệ số cần tìm là :
.
9
9 6
12
220
1 3
729
C
Cohangxom1991@gmail.com
Câu 24. Khối nón có bán kính đáy bằng diện tích xung quanh bằng . Tính thể tích của
( )N
3
15
V
khối nón .
( )N
A. . B. . C. . D. .
36V
60V
20V
12V
Lời giải
Tác giả : Phạm Văn Huy, FB: Đời Dòng
Chọn D
Ta có .
15
5
3
xq
xq
S
S rl l
r
Chiều cao .
2 2
25 9 4h l r
.
2 2
1 1
.3 .4 12
3 3
V r h
trichinhsp@gmail.com
Câu 25. Cho tứ diện có . Khẳng định nào sau đây là đúng?
ABCD
,AB AC DB DC
A. . B. . C. . D. .
AB BC
CD ABD
BC AD
AB ABC
Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn trí Chính
I
D
C
B
A
Chọn C
Gọi I là trung điểm BC.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 14 Mã đề 101
Có , . Suy ra là trung trực của . Nên
AB AC
IB IC
AI
BC
BC AI
Tương tự
BC DI
Suy ra . Suy ra . Chọn C
BC AID
BC AD
nguyentuanblog1010@gmail.com
Câu 26. Cho phương trình . Tính tổng các nghiệm thuộc khoảng của
3
sin 2 sin
4 4
x x
0;
phương trình trên.
A. . B. . C. . D. .
7
2
3
2
4
Lời giải
Tác giả : Phạm Chí Tuân, FB: Tuân Chí Phạm
Chọn B
Ta có: .
3
2
2 2
3
4 4
sin 2 sin
2
3
4 4
2 2
6 3
4 4
x k
x x k
x x
x k
x x k
k !
+ Xét .
2x k
k !
Do . Vì nên không có giá trị .
1
0 0 2 0
2
x k k
k !
k
+ Xét .
2
6 3
x k
k !
Do . Vì nên có hai giá trị là: .
2 1 5
0 0
6 3 4 4
x k k
k !
k
0; 1k k
Với .
0
6
k x
Với .
5
1
6
k x
Do đó trên khoảng phương trình đã cho có hai nghiệm và .
0;
6
x
5
6
x
Vậy tổng các nghiệm của phương trình đã cho trong khoảng là: .
0;
5
6 6
tuluc0201@gmail.com
Câu 27. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A. . B. . C. . D. .
2 3
2
x
y
x
4
y x
3
y x x
2y x
Lời giải
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 15 Mã đề 101
Tác giả : Võ Tự Lực, FB: Võ Tự Lực
Chọn A.
+ Hàm số
2 3
2
x
y
x
Tập xác định: .
; 2 2;D  
Có hàm số luôn đồng biến trên từng khoảng xác định hàm số
2
7
' 0
2
y x D
x
không có cực trị.
Các hàm số khác dễ dàng chứng minh được y’ có nghiệm và đổi dấu qua các nghiệm. Riêng
hàm số cuối y’ không xác định tại -2 nhưng hàm số xác định trên R và y’ đổi dấu qua -2 do đó
có hàm số có điểm cực trị x = -2.
(tien.vuviet@yahoo.com)
Câu 28. Có bao nhiêu tiếp tuyến của đồ thị đi qua giao điểm của hai đường tiệm cận?
2 3
2
x
y
x
A. . B. Không có. C. Vô số. D. .
1
2
Lời giải
Tác giả : Vũ Việt Tiến, FB: Vũ Việt Tiến
Chọn B
Đồ thị hàm số nhận đường thẳng làm tiệm cận đứng.
2
d
x
c
Đồ thị hàm số nhận đường thẳng làm tiệm cận ngang.
2
a
y
c
Vậy là giao điểm của hai đường tiệm cận.
2;2I
TXĐ:
D !
2
7
'
( 2)
y
x
Gọi tiếp tuyến tại của đồ thị hàm số có dạng:
0 0
;M x y
2 3
2
x
y
x
hay
0 0 0
: ' .( )y y x x x y
0
0
2
0 0
2 3
7
: .( )
( 2) 2
x
y x x
x x
Vì đi qua
0
0
2
0 0
2 3
7
2;2 .( 2 )
( 2 2
2
)
x
I x
x x
0 0
0
2
0 0 0 0
2 3 2 3
7 7
.( 2)
( 2) 2 ( 2) 2
2 2
x x
x
x x x x
, phương trình vô nghiệm.
0
0
2 10
4 12 0
2
x
x
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 16 Mã đề 101
Vậy không tồn tại tiếp tuyến nào của đồ thị hàm số mà đi qua giao điểm của hai
2 3
2
x
y
x
tiệm cận.
tien.vuviet@yahoo.com
Câu 29. Trong mặt phẳng tọa độ cho tam giác có lần lượt là trung
Oxy
ABC
3;4 , 6;1 , 7;3D E F
điểm các cạnh .Tính tổng tung độ ba đỉnh của tam giác .
, ,AB BC CA
ABC
A. . B. . C. . D. .
16
3
8
3
8
16
Lời giải
Tác giả: Vũ Việt Tiến, FB: Vũ Việt Tiến
Chọn C
Ta có
2 2.4 8
2 2.3 6 2 8 6 2 16
2 2.1 2
A B D
A C F A B C
B C E
y y y
y y y y y y
y y y
. Chọn C.
8
A B C
y y y
Nguyentinh050690@gmail.com.
Câu 30. Cho hình chóp có đáy là tam giác vuông cân, ,
.S ABC
ABC
!
!
0
, 90 BA BC a SAB SCB
biết khoảng cách từ đến bằng . Góc giữa và mặt phẳng là:
A
SBC
3
2
a
SC
ABC
A. . B. . C. . D. .
6
3
rccos
4
a
3
4
Lời giải
Tác giả: Nguyễn Tình, FB: Gia Sư Toàn Tâm.
Chọn C
H
D
C
B
A
S
Gọi là hình chiếu vuông góc của lên .
D
S
ABC
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 17 Mã đề 101
là hình chiếu vuông góc của lên .
H
D
SC
Khi đó: .
AB SA
AB SAD AB AD
AB SD
BC SC
BC SDC BC DC
BC SD
là hình vuông và .
ABCD
CD a
Ta có: .
, ,
3
|| ||
2
A SBC D SBC
a
AD BC AD SBC d d DH DH
Vì là hình chiếu vuông góc của lên mặt phẳng nên là góc giữa
DC
SC
ABCD
!
SCD
đường thẳng và .
SC
ABC
! !
3
sin
2 3
DH
SCD SCD
DC
lientoanc3@gmail.com
Câu 31. Cho hàm số có đồ thị . Có bao nhiêu điểm thuộc sao cho tiếp tyến của
4 2
1
3
4
y x x
( )C
A
( )C
tại cắt tại hai điểm phân biệt , khác ) thỏa mãn
( )C
A
( )C
1 1
( ; )M x y
2 2
( ; )N x y
( ,M N
A
1 2 1 2
5( )y y x x
A. . B. . C. . D. .
1
2
0
3
Lờigiải
Tác giả: Nguyễn Thị Kim Liên; FB: Kim Liên
Chọn B
3
' 6y x x
Gọi là tọa độ tiếp điểm của tiếp tuyến tại A. Phương trình tiếp tuyến tại A là
4 2
0 0 0
1
( ; 3 )
4
A x x x
đường thẳng (d) có phương trình:
3 4 2
0 0 0 0 0
1
( 6 )( ) 3
4
y x x x x x x
Phương trình hoành độ giao điểm của (d) và (C) là:
3 4 2 4 2
0 0 0 0 0
1 1
( 6 )( ) 3 3
4 4
x x x x x x x x
2 2 2
0 0 0
( ) ( 2 3 12) 0x x x x x x
0
2
0 0
0
2 3 12 0 (2)
x x
x x x x
(d) cắt (C) tại hai điểm phân biệt khác A khi và chỉ chi phương trình (2) có hai nghiệm phân
biệt khác
0
x
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 18 Mã đề 101
0
0
2
(3)
6 6
x
x
Khi đó, phương trình (2) có hai nghiệm phân biệt và (d) cắt (C) tại hai điểm phân biệt
1 2
,x x
, trong đó:
1 1
( ; )M x y
2 2
( ; )N x y
3 4 2
1 0 0 1 0 0 0
1
( 6 )( ) 3
4
y x x x x x x
3 4 2
2 0 0 2 0 0 0
1
( 6 )( ) 3
4
y x x x x x x
3
1 2 0 0 1 2
( 6 )( )y y x x x x
Từ giả thiết ta suy ra:
(Vì )
3
0 0 1 2 1 2
( 6 )( ) 5( )x x x x x x
3
0 0
6 5 x x
1 2
x x
0
0
0
1
1 21
2
1 21
2
x
x
x
Kết hợp với điều kiện
(3) có hai giá trị thỏa mãn
0
x
yêu cầu bài toán là
0
0
1
1 21
2
x
x
cunconsieuquay1408@gmail.com
Câu 32. Giả sử đồ thị hàm số có 3 điểm cực trị là mà
2 4 2 2
1 2 1y m x mx m
, ,A B C
. Khi quay tam giác quanh cạnh ta được một khối tròn xoay. Giá trị của
A B C
x x x
ABC
AC
để thể tích của khối tròn xoay đó lớn nhất thuộc khoảng nào trong các khoảng dưới đây:
m
A. . B. . C. . D. .
4;6
2;4
2;0
0;2
Lời giải
Tác giả: Nguyễn Thị ThanMai, FB: Thanh Mai Nguyen
Chọn B
r
h
I
C
B
A
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 19 Mã đề 101
2 3 2 2
4( 1) 4 4 ( 1) -y m x mx x m x m
+
2 2
2
0
0 4 ( 1) - 0
( 0)
1
x
y x m x m
m
x m
m
+ Với thì đồ thị hàm số có 3 điểm cực trị (với ) là:
0m
A B C
x x x
; ; .
2
2
2 2
( ; - 1)
1 1
m m
A m
m m
2
(0; 1)B m
2
2
2 2
( ; - 1)
1 1
m m
C m
m m
+ Quay quanh thì được khối tròn xoay có thể tích là:
ABC
AC
.
2 2
1 2
2. . .
3 3
V r h BI IC
2
2 9
2 2 5
2
2 2
.
3 3
1 1
1
m m m
m m
m
+ Xét hàm số
9
5
2
( )
1
m
f x
m
Có: ; .
8 2
6
2
(9 - )
'( )
1
m m
f x
m
( ) 0 3 ( 0)
f x m m
Ta có BBT:
3
–
max
x
0

f x
0
f x
0
0
Vậy thể tích cần tìm lớn nhất khi .
3m
ptpthuyedu@gmail.com
Câu 33. Giải phương trình
8.cos 2 .sin 2 .cos4 2x x x
A. . B. .
32 4
( )
3
32 4
x k
k
x k
!
( )
3
8 8
8 8
x k
k
x k
!
C. . D. .
32 4
( )
5
32 4
x k
k
x k
!
( )
3
16 8
16 8
x k
k
x k
!
Lời giải
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 20 Mã đề 101
Tác giả : Phạm Thị Phương Thúy, FB: Thuy phạm
Chọn C
8.cos 2 .sin 2 .cos4 2 4.sin 4 .cos4 2 2.sin8 2
8 2
2
32 4
4
sin8 ( ) ( )
2
5 5
8 2
4 32 4
x x x x x x
x k
x k
x k k
x k x k
! !
tcdung.math@gmail.com
Câu 34. Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên
2
2
log 2
log 1
m x
y
x m
4;
A. hoặc . B. hoặc .
2m
1m
2m
1m
C. hoặc . D. .
2m
1m
2m
Lời giải
Tác giả : Trần Công Dũng, FB: trancong.dung.948
Chọn D
Đặt .
2
logt x
Ta có .
4; 2;x t  
Hàm số được viết lại (1).
2
1
mt
y
t m
Vì đồng biến trên nên yêu cầu bài toán (1) nghịch biến trên
2
logt x
0;
2;
.
2
1 2 0
2
1
1 2
1
m
m m
m
m
m
m
mp01100207@gmail.com
Câu 35. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào
?
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 21 Mã đề 101
A. . B. . C. . D. .
2 1
2 1
x
y
x
1
1
x
y
x
2
1
x
y
x
1
x
y
x
Lời giải
Tác giả : Minh Anh Phuc, FB: Minh Anh Phuc
Chọn B
Từ đồ thị của hàm số đã cho ta có:
Tiệm cận đứng của đồ thị hàm số là đường thằng có phương trình .
1 x
Tiệm cận ngang của đồ thị hàm số là đường thằng có phương trình .
1 y
Đồ thị hàm số đi qua các điểm và .
1;0
0;1
Suy ra hàm số cần tìm là .
1
1
x
y
x
Đangvanquanggb1@gmail.com
Câu 36. Cho hàm số . Tìm tất cả các giá trị của tham số để hàm số
3 2
2 1 3 2y x m x m x
m
có điểm cực trị.
y f x
3
A. . B. . C. 3. D. .
3m
3m
1
2
m
1
3
2
m
Lời giải
Tácgiả :Đặng Văn Quang, FB: DangQuang
Chọn A
Hàm số
3 2
2 1 3 2y x m x m x
TXĐ:
!
2
3 2 2 1 3y x m x m
Hàm số có ba điểm cực trị khi và chỉ khi phương trình có hai nghiệm
y f x
0y
1 2
,x x
thỏa mãn .
1 2
0x x
Trường hợp 1: Phương trình
có hai nghiệm
0y
1 2
0 3 3 0 3x x m m
Trường hợp 2: Phương trình
có hai nghiệm
0y
1 2
0x x
Có
0 0 3y m
Với thì (thỏa mãn)
3m
2
0
3 14 ; 0
14
0
3
x
y x x y
x
Vậy với thì hàm số
có ba điểm cực trị.
3m
y f x
Tranquocan1980@gmail.com
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 22 Mã đề 101
Câu 37. Có bao nhiêu số tự nhiên có 3 chữ số sao cho là độ dài 3 cạnh của một tam giác cân.
abc
, ,a b c
A.45. B.216. C.81. D.165.
Lờigiải
Tácgiả :Trần Quốc An, FB: TranQuocAn
Chọn D
TH1: là độ dài 3 cạnh của một tam giác đều.
, ,a b c
Trường hợp này có 9 số thỏa mãn yêu cầu bài toán.
TH2 : là độ dài 3 cạnh của một tam giác cân và không đều.
, ,a b c
Không làm mất tính tổng quát, giả sử .
a b
*)
a b c
+
2 1.a b c
+
3 1,2.a b c
+
4 1,2,3.a b c
………..
+
9 1,2,3,...,8a b c
Có : số thỏa bài toán.
1 2 3 .. 8 36
*)
a b c
Do
.
2
c
a b c a c
+
9
9 9 5,6,7,8.
2
c a a
+
8 4 8 5,6,7.c a a
+
7
7 7 4,5,6
2
c a a
+
6 3 6 4,5.c a a
+
5
5 5 3,4.
2
c a a
+
4 2 4 3c a a
+
3
3 3 2.
2
c a a
+ không có a tương ứng.
2,1c
Có : số thỏa bài toán.
4 3 3 2 2 1 1 16
Trong trường hợp , có : số thỏa mãn.
a b c
36 16 52
Tương tự, mỗi trường hợp , đều có 52 số thỏa mãn.
b c a
c a b
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 23 Mã đề 101
Theo quy tắc cộng ta có: số thỏa mãn yêu cầu bài toán bài toán.
9 52.3 165
Nguyenvandiep1980@gmail.com
Câu 38. Trong mặt phẳng tọa độ , cho tam giác có . Gọi là
Oxy
ABC
3 0 3 0 2 6A ; ,B ; ,C ;
H a;b
trực tâm của tam giác . Tính
ABC
6ab
A. 10. B. . C. 60. D. 6.
5
3
Lời giải
Tác giả : Nguyễn Văn Điệp, FB: Nguyễn Văn Điệp
Chọn A
H
A
B
C
Đường thẳng đi qua và nhận làm véctơ pháp tuyến. Suy ra
AH
3 0A ;
1 6BC ;
phương trình đường thẳng là: .
AH
6 3 0x y
Đường thẳng đi qua và nhận làm véctơ pháp tuyến. Suy ra phương
BH
3 0B ;
5 6AC ;
trình đường thẳng là: .
BH
5 6 15 0x y
Ta có Tọa độ là nghiệm của hệ
6 3
5 6 15 0
0
5
2
6
x y
x y
H ;
.
H AH BH
H
Do đó .
5
2 6 10
6
a ;b ab
lanthangqn@gmail.com
Câu 39. Một chiếc thùng chứa đầy nước có hình một khối lập phương. Đặt vào trong thùng đó một khối
nón sao cho đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với
các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước trào ra ngoài và lượng nước còn lại
ở trong thùng.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 24 Mã đề 101
A. . B. . C. . D. .
12
1
11
12
11
12
Lời giải
Tác giả : Nguyễn Thị Lan, FB: Nguyen Thi Lan
Chọn A
Coi khối lập phương có cạnh . Thể tích khối lập phường là .
1
1V
Từ giả thiết ta suy ra khối nón có chiều cao , bán kính đáy .
1h
1
2
r
Thể tích lượng nước trào ra ngoài là thể tích của khối nón.
1
V
Ta có: .
2
1
1 1 1
. .1
3 3 4 12
V r h
Thể tích lượng nước còn lại trong thùng là: .
2 1
12
1
12 12
V V V
Do đó: .
1
2
12
V
V
Damvanthuong1205@gmail.com
Câu 40. Cho giới hạn (phân số tối giản). Giá trị của là
3
1 5 1
lim
4 3
x
x x a
b
x x
2T a b
A. . B. . C. . D. .
1
9
1
10
9
8
Lời giải
Tác giả : Đàm Văn Thượng, FB: Thượng Đàm
Chọn C
2
2
3 3
3 4 3
1 5 1
lim lim
4 3
4 3 1 5 1
x x
x x x x
x x
x x
x x x x
3
4 3
3. 3 3
9
lim .
2. 4 4 8
1 1 5 1
x
x x x
x x x
Vậy .
2 10T a b
Email: buichithanh1987@gmail.com
Câu 41. Cho tứ diện . Gọi
lần lượt là trung điểm của
và .
là điểm thuộc đoạn
ABCD
,K L
AB
BC
N
sao cho . Gọi là giao điểm của với mặt phẳng . Tính tỉ số
CD
2CN ND
P
AD
( )KLN
PA
PD
A. . B. . C. . D. .
1
2
PA
PD
2
3
PA
PD
3
2
PA
PD
2
PA
PD
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 25 Mã đề 101
Lời giải
GV giải : Bùi Chí Thanh Facebook: Thanhbui
Chọn D
P
B
D
C
A
I
K
L
N
Giả sử . Nối với cắt
tại Suy ra
LN BD I
K
I
AD
P
( )KLN AD P
Ta có: Suy ra:
/ / / /KL AC PN AC
2
PA NC
PD ND
ptpthuyedu@gmail.com
Câu 42. Tìm số nghiệm của phương trình
2 2
log log ( 1) 2x x
A. 0. B. 1. C. 3. D. 2.
Lời giải
Tác giả : Phạm Thị Phương Thúy, FB: Thuy pham
Chọn B
Điều kiện:
1x
Ta có:
2 2
log log ( 1) 2x x
2
2
log [ ( 1)] 2 ( 1) 4 4 0
1 17
2
1 17
2
x x x x x x
x
x
Đối chiếu với điều kiện ta được nghiệm của phương trình là .
1 17
2
x
Vnhtk2017@gmail.com
Câu 43. Hàm số xác định với mọi giá trị của khi.
2
ln 1y x mx
x
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 26 Mã đề 101
A. . B. . C. . D. .
2
2
m
m
2m
2 2m
2m
Lời giải
Tác giả : Phạm Văn Nghiệp, FB: Phạm Văn Nghiệp
Chọn C
Yêu cầu bài toán , .
2
1 0x mx
x !
2
4 0m
2 2m
ngoletao@gmail.com
Câu 44. Trong một lớp có học sinh gồm An, Bình, Chi cùng học sinh khác. Khi xếp tùy ý
2 3n
2n
các học sinh này vào một dãy ghế được đánh số từ đến , mỗi học sinh ngồi một ghế thì
1
2 3n
xác suất để số ghế của An, Bình, Chi theo thứ tự lập thành một cấp số cộng là . Số học sinh
17
1155
của lớp là
A. . B. . C. . D. .
27
25
45
35
Lời giải
Tác giả : Ngô Lê Tạo, FB: Ngô Lê Tạo
Chọn D
Số cách các xếp học sinh vào ghế là .
2 3 !n
Nhận xét rằng nếu ba số tự nhiên lập thành một cấp số cộng thì nên là
, ,a b c
2a c b
a c
một số chẵn. Như vậy phải cùng chẵn hoặc cùng lẻ.
,a c
Từ đến có số chẵn và số lẻ.
1
2 3n
1n
2n
Muốn có một cách xếp học sinh thỏa số ghế của An, Bình, Chi theo thứ tự lập thành một cấp số
cộng ta sẽ tiến hành như sau:
Bước 1: chọn hai ghế có số thứ tự cùng chẵn hoặc cùng lẻ rồi xếp An và Chi vào, sau đó xếp
Bình vào ghế chính giữa. Bước này có cách.
2 2
1 2n n
A A
Bước 2: xếp chỗ cho học sinh còn lại. Bước này có cách.
2n
2 !n
Như vậy số cách xếp thỏa yêu cầu này là .
2 2
1 2
. 2 !
n n
A A n
Ta có phương trình
2 2
1 2
2
. 2 !
1 1 2
17 17
2 3 ! 1155 2 1 2 2 2 3 1155
68 1019 1104 0
16
69
( )
68
n n
A A n
n n n n
n n n n
n n
n
n
loaïi
Vậy số học sinh của lớp là .
35
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 27 Mã đề 101
tanbaobg@gmail.com
Câu 45. Cho một hình lập phương có cạnh bằng . Tính theo thể tích của khối bát diện đều có các đỉnh
a
a
là tâm các mặt của hình lập phương.
A. . B. . C. . D. .
3
1
4
a
3
1
6
a
3
1
12
a
3
1
8
a
Lời giải
Tác giả : Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo
Chọn B
Giả sử hình lập phương có cạnh bằng và tâm các mặt là
.ABCD A B C D
a
, , , , ,P Q R S O O
như hình vẽ.
Ta có là đường trung bình của tam giác đều cạnh nên .
PQ
B CD
2a
2
2
a
PQ
Do đó và .
2 2
1
2
PQRS
S PQ a
OO a
Vậy thể tích bát diện cần tìm là (đvtt).
3
1 1
.
3 6
PQRS
V S OO a
builoiyka@gmail.com
Câu 46. Đồ thị hàm số đối xứng với đồ thị hàm số qua điểm . Giá trị
y f x
0, 1
x
y a a a
1;1I
của biểu thức bằng
1
2 log
2018
a
f
A. . B. . C. . D. .
2016
2016
2020
2020
Lờigiải
Tác giả : Bùi Thị Lợi, FB: Loi Bui
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 28 Mã đề 101
Chọn B
Gọi là đồ thị hàm số ; là đồ thị hàm số .
C
x
y a
1
C
y f x
.
1
1
2 log ;
2018
a M
M y C
1
2 log
2018
M a
y f
Gọi đối xứng với qua .
N
M
1;1I
1
log ;2
2018
a M
N y
Do đồ thị đối xứng qua nên .
1
C
C
1;1I
1
log ;2
2018
a M
N y C
.
N C
1
log
2018
2
a
M
y a
log 2018
2
a
M
y a
2 2018
M
y
2016
M
y
Vậy .
1
2 log 2016
2018
a
f
nguyentuyetle77@gmail.com
Câu 47. Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên
3 2
sin 3cos sin 1y x x m x
3
;
2
A. . B. . C. . D. .
3m
0m
3m
0m
Lời giải
Tác giả : NguyễnTuyết Lê, FB: Nguyen Tuyet Le
Chọn B
Ta có: .
3 2
( ) sin 3sin sin 4y f x x x m x
(1)
Đặt , do .
sint x
3
; 1;0
2
x t
Hàm số trở thành
.
(1)
3 2
(t) 3 4(2)y g t t mt
Hàm số đồng biến trên khi và chỉ khi hàm số nghịch biến trên
(1)
3
;
2
(2)
1;0
( tại hữu hạn điểm).
,
(t) 0, 1;0g t
,
(t) 0g
Hàm số trên , ta có
.
3 2
(t) 3 4y g t t mt
1;0
, 2
(t) 3 6g t t m
Suy ra:
,
(t) 0, 1;0g t
2
3 6 0, 1;0t t m t
2
3 6 , 1;0t t m t
Xét hàm số trên đoạn
.
2
(t) 3 6y h t t
1;0
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 29 Mã đề 101
Ta có đồng biến trên .
'
(t) 6 6 0, 1;0h t t
( )h t
1;0
max
[
‒
1;0
]
ℎ(𝑡)
=
ℎ
(
0
)
=
0
Tức .Do đó có .
,
(t) 0, 1;0g t
max
[
‒
1;0
]
ℎ(𝑡)
≤
𝑚 ∀𝑡
∈
[
‒
1;0
]
0m
Hàm số đồng biến trên khi và chỉ khi .Chọn đáp án B
(1)
3
;
2
0;m 
luuquihien@gmail.com
Câu 48. Một cái phễu có dạng hình nón chiều cao của phễu là . Người ta đổ một lượng nước vào
30cm
phễu sao cho chiều cao của cột nước trong phễu bằng (hình ). Nếu bịt kín miệng phễu
15cm
1
H
rồi lật ngược phễu lên ( hình ) thì chiều cao của cột nước trong phễu gần với giá trị nào sau
2
H
đây ?
H2
H1
A. . B. . C. D. .
1,553 cm
1,306 cm
1,233 cm
15 cm
Lời giải
Tác giả : Lưu Quí Hiền, FB: lưu quí hiền
Phản biện: Nguyễn Đức Duẩn
Chọn B
M
A
O
E
N
P
O
A
E
Q
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 30 Mã đề 101
Phễu có dạng hình nón, gọi là đỉnh, đáy là đường tròn tâm , bán kính
E
O
OA
chiều cao .
30OE cm
Gọi là thể tích của khối nón có đỉnh , đáy là đường tròn tâm , bán kính .
V
E
O
OA
Ta có
2 2
1
. . 10
3
V OA OE OA
Gọi là trung điểm của đoạn , là trung điểm của đoạn .Khi đổ nước vào phễu
M
OE
N
EA
chiều cao của cột nước là .
15EM cm
Gọi là thể tích của khối nón có đỉnh , đáy là đường tròn tâm , bán kính .
1
V
E
M
MN
Thể tích nước là
2 2 2
1
1 5
. . 5 . .
3 4
V MN EM MN OA
1
1
8
V V
Khi bịt kín miệng phễu rồi lật ngược phễu lên, chiều cao của cột nước là .
OP
Gọi là thể tích của khối nón có đỉnh , đáy là đường tròn tâm , bán kính
2
V
E
P
PQ
Ta có
2
2 1
7 7
8 8
V
V V V V
V
2
2
1
. .
7
3
1
8
. .
3
PQ PE
OA OE
2
2
. 7
1
. 8
PQ PE
OA OE
Ta có vuông tại và vuông tại có
PEQ
P
OEA
O
!
!
OEA PEQ
và đồng dạng
PEQ
OEA
PQ PE
OA OE
Do đó
3
7
1
8
PE
OE
3
7
2
PE
OE
3
7
2
OE OP
OE
3
7
1
2
OP OE
3
7
30 1
2
1,306cm
phunghang10ph5s@gmail.com
Câu 49. Hàm số có tập xác định là thì
2
log 4 2
x x
y m
!
A. . B. . C. . D. .
1
4
m
0m
1
4
m
1
4
m
Lời giải
Tác giả : Phùng Hằng, FB: Hằng Phùng
Phản biện: Nguyễn Đức Duẩn
Chọn D
Điều kiện xác định:
4 2 0
x x
m
Hàm số đã cho có tập xác định là (*)
4 2 0, 4 2 ,
x x x x
m x m x ! ! !
Đặt
2 , 0
x
t t
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 31 Mã đề 101
Khi đó (*) trở thành với
2
, 0m t t t
0;
max ( )m f t

2
( ) , 0f t t t t
Ta có: ,
' 2 1f t t
1
' 0
2
f t t
Bảng biến thiên của hàm số :
2
( ) , 0f t t t t
t
0
1
2

'f t
+
0
-
f t
0
1
4

Từ BBT ta thấy đạt được khi
0;
1
max ( )
4
f t

1
2
t
Vậy
0;
1
max
4
m f t m

Duanquy@gmail.com
Câu 50. Cho hình thang vuông có đường cao , các cạnh đáy và . Gọi
ABCD
2AB a
AD a
3BC a
là điểm trên đoạn sao cho . Tìm để
M
AC
AM k AC
k
BM CD
A. . B. . C. . D. .
4
9
3
7
1
3
2
5
Lời giải
Tác giả : Nguyễn Đức Duẩn
Chọn D
Chọn hệ trục tọa độ như hình vẽ sao cho gốc tọa độ trùng với điểm , điểm thuộc trục
B
A
Oy
và điểm thuộc trục .
C
Ox
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 32 Mã đề 101
Theo bài ra ta có
(0;0), (0;2), (3;0), (1;2)B A C D
Khi đó . Phương trình tham số của đường thẳng là
(3; 2)AC
AC
x 3t
y 2 2t
,t !
Gọi . Ta có và
(3 ;2 2 )M AC M t t
(3 ;2 2 )BM t t
(2; 2)DC
Để thì
BM DC
2
. 0 6 4 4 0
5
BM DC t t t
6 6
;
5 5
M
Khi đó và
6 4 52
;
5 5 5
AM AM
3; 2 13AC AC
Vì và cùng chiều
AM k AC
,AM AC
52 2
5
5 13
AM
k
AC
| 1/39
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT TỈNH BẮC NINH
ĐỀ THI KHẢO SÁT LẦN 2 – NĂM HỌC 2018 - 2019
TRƯỜNG THPT CHUYÊN BẮC NINH MÔN: TOÁN 12
Thời gian làm bài : 90 Phút (không kể thời gian giao đề) (Đề có 05 trang)
(Đề có 50 câu trắc nghiệm)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 101 1
Câu 1: Giá trị lớn nhất của hàm số 3 2 y 2x 3x 1 trên đoạn ;1 2 A. max y 4. B. max y 6. C. max y 3. D. max y 5. 1 1 1 1 ;1 ;1 ;1 ;1 2 2 2 2
Câu 2: Xét các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song songvới nhau.
D. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau.
Câu 3: Một hình trụ có bán kính đáy r a , độ dài đường sinh l  2a . Diện tích toàn phần của hình trụ này là: 2 A. 2 2 a . B. 2 4 a .
C. 6 a . D. 2 5 a .
Câu 4: Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó? A. 1 B. 2 C. Không có D. Vô số
Câu 5: Tập nghiệm của bất phương trình 2x 1 3   27 là:  1   1  A. 3;  B. ;    C. ;    D. 2;   3   2 
Câu 6: Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực ? x    x  2 
A. y  log x . B. y . C. y .
D. y  log  2 2x   1. 1      3   e  2 4
Câu 7: Cho hàm số f có đạo hàm trên khoảng I . Xét các mệnh đề sau:
(I). Nếu f  x  0 , x
  I thì hàm số nghịch biến trên I .
(II). Nếu f  x  0 , x
  I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số nghịch biến trên I .
(III). Nếu f  x  0 , x
  I thì hàm số nghịch biến trên khoảng I .
(IV). Nếu f  x  0 , x
  I và f x  0 tại vô số điểm trên I thì hàm số f không thể nghịch biến trên khoảng I .
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
A. I, II và IV đúng, còn III sai.
B. I, II, III và IV đúng.
C. I và II đúng, còn III và IV sai.
D. I, II và III đúng, còn IV sai.
Câu 8: Một nhóm có 10 người, cần chọn ra ban đại diện gồm 3 người. Số cách chọn là: A. 240. B. 3 A . C. 3 C . D. 360. 10 10
Câu 9: Trong mặt phẳng tọa độ Oxy cho bốn điểm A3; 5  , B 3  ;3 , C 1  ; 2  , D5; 1  0. Hỏi  1  G ; 3  
 là trọng tâm của tam giác nào dưới đây?  3 
Trang 1/6 - Mã đề thi 101 A. ABC. B. BCD. C. A . CD D. . ABD
Câu 10: Tập xác định của hàm số y   x  15 1 là:
A. 0;   .
B. 1;   .
C. 1;   . D. .
Câu 11: Trong các hàm số sau, hàm số nào là hàm số chẵn.
A. y  tan x
B. y  sin x
C. y  cos x
D. y  cot x
Câu 12: Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số 3 2
y x  3x  2 . Mệnh đề nào dưới đây đúng?
A. d có hệ số góc dương.
B. d song song với đường thẳng x 3 .
C. d có hệ số góc âm.
D. d song song với đường thẳng y 3 .
Câu 13: Hình lập phương có mấy mặt phẳng đối xứng ? A. 6 B. 8 C. 9 D. 7
Câu 14: Trong các dãy số sau, dãy nào là cấp số cộng: 2 5n  2 A. n 1 u 3   . B. u  . C. 2 u n 1. D. u  . n n n 1 n n 3 u   5 Câu 15: Cho dãy số 1 (u ) : 
. Số 20 là số hạng thứ mấy trong dãy? n uu nn 1 n A. 5. B. 6. C. 9. D. 10. Câu 16: x
A và B là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số y  . Khi đó độ dài x  2
đoạn AB ngắn nhất bằng A. 4 2 . B. 4 . C. 2 . D. 2 2 .
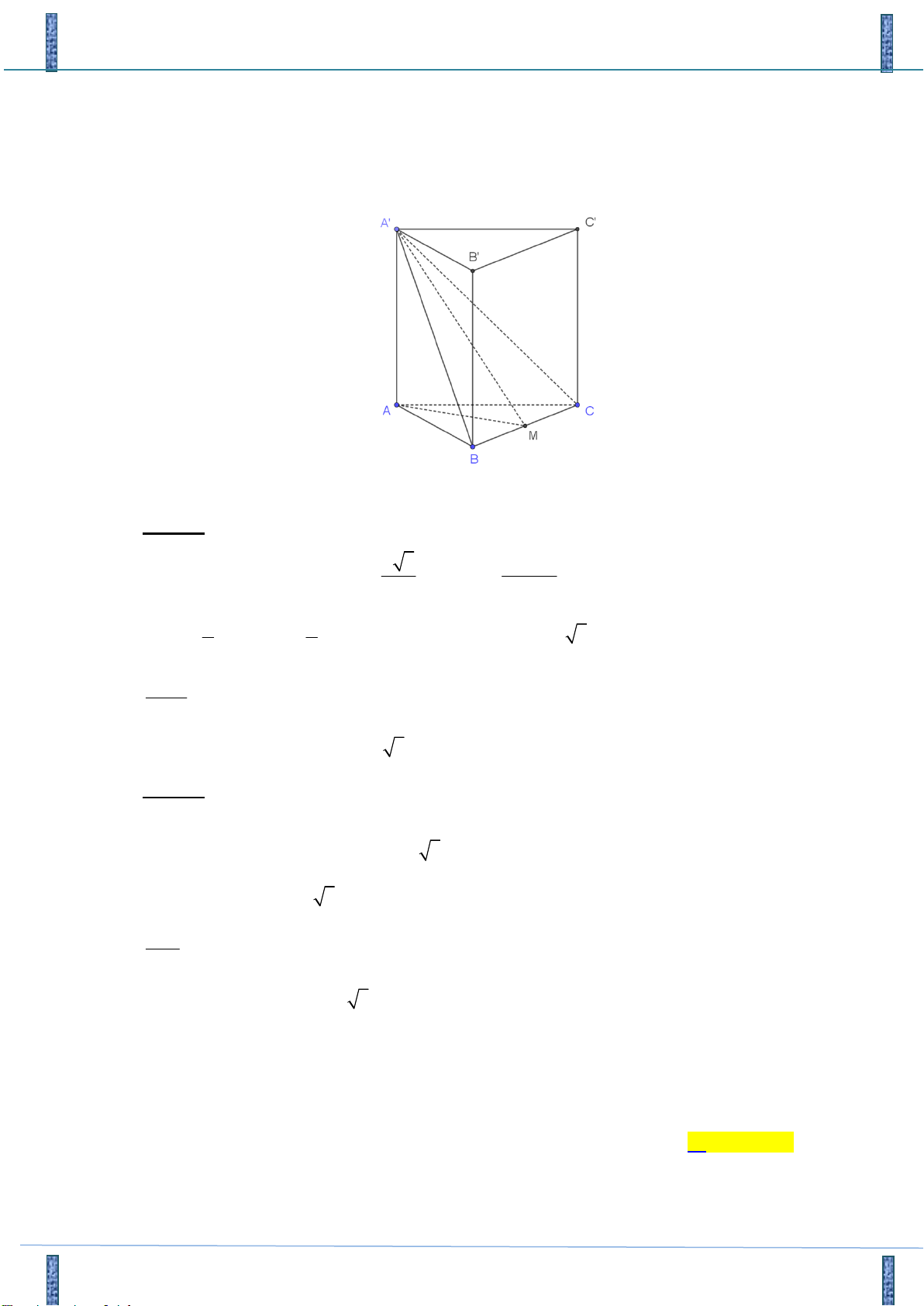
Câu 17: Cho hình lăng trụ đều ABC.A BC
 . Biết mặt phẳng (A BC) tạo với mặt phẳng (ABC) một góc
30 và tam giác A BC có diện tích bằng 2
8a . Tính thể tích khối lăng trụ ABC.A BC  . 3 8a 3 3 8a A. 3 8a 3. B. 3 8a . C. . D. . 3 3
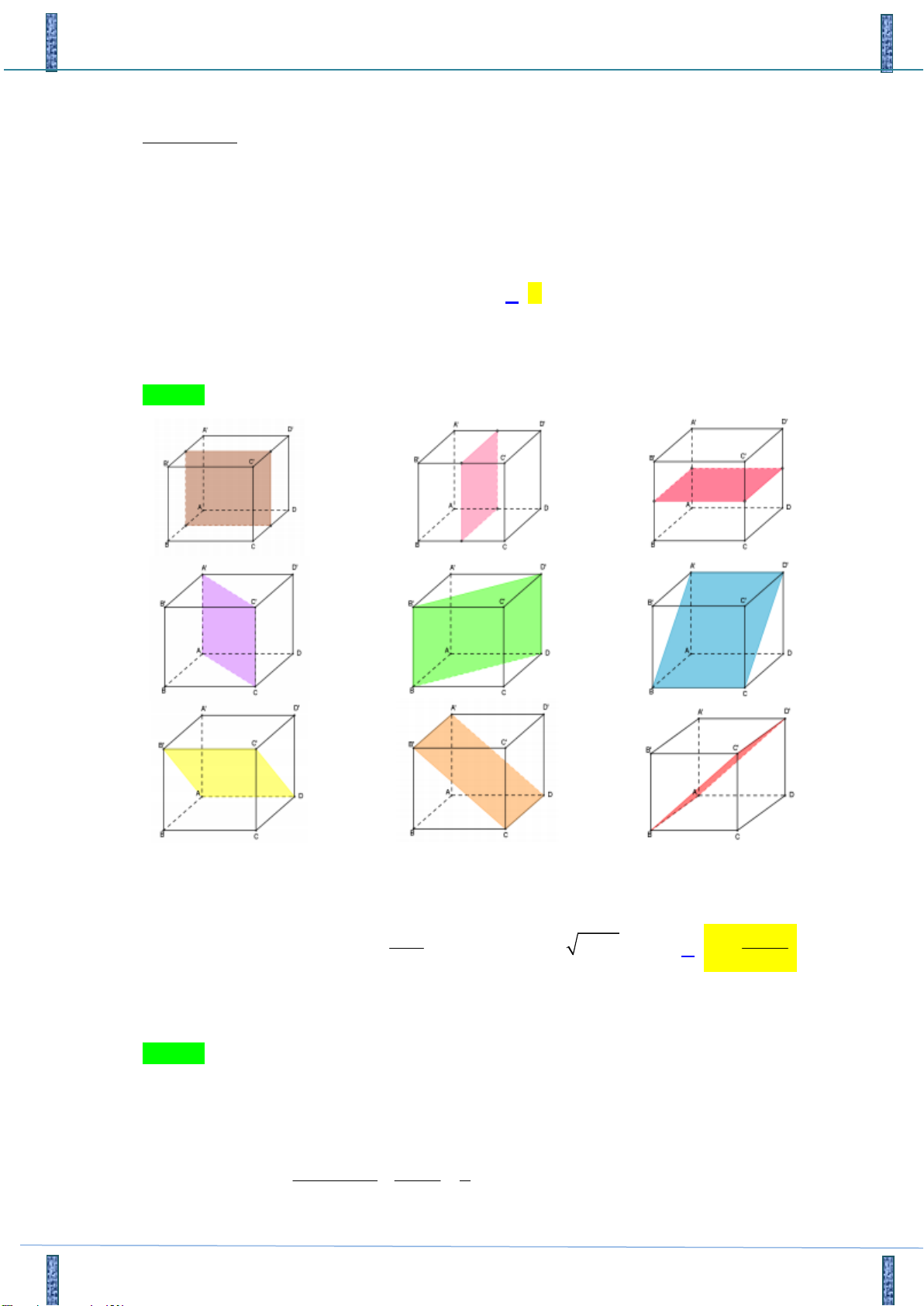
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm thuộc đoạn SB (M
khác S và B). Mặt phẳng  ADM  cắt hình chóp S.ABCD theo thiết diện là A. Hình bình hành. B. Tam giác C. Hình chữ nhật. D. Hình thang.
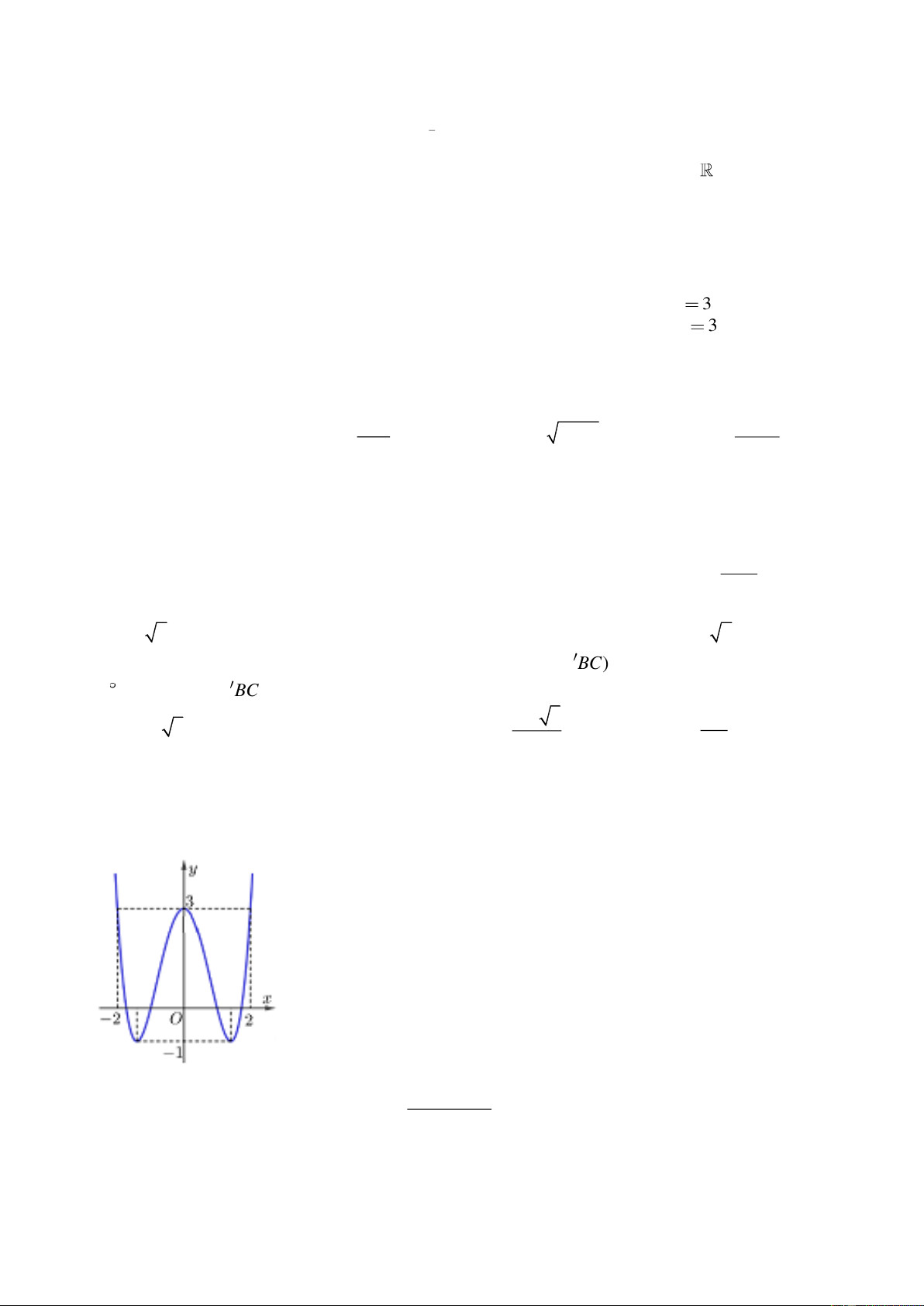
Câu 19: Hàm số nào sau đây có đồ thị như hình bên? A. 4 2
y  x  4x  3 B. 4 2
y  x  2x  3
C. y   x  2 2 2 1
D. y   x  2 2 2 1 Câu 20: 1
Tìm tập xác định của hàm số y  log 5 x 2   A.  ;  5 \  4 . B. 5; . C.  ;  5. D. 5;.
Trang 2/6 - Mã đề thi 101
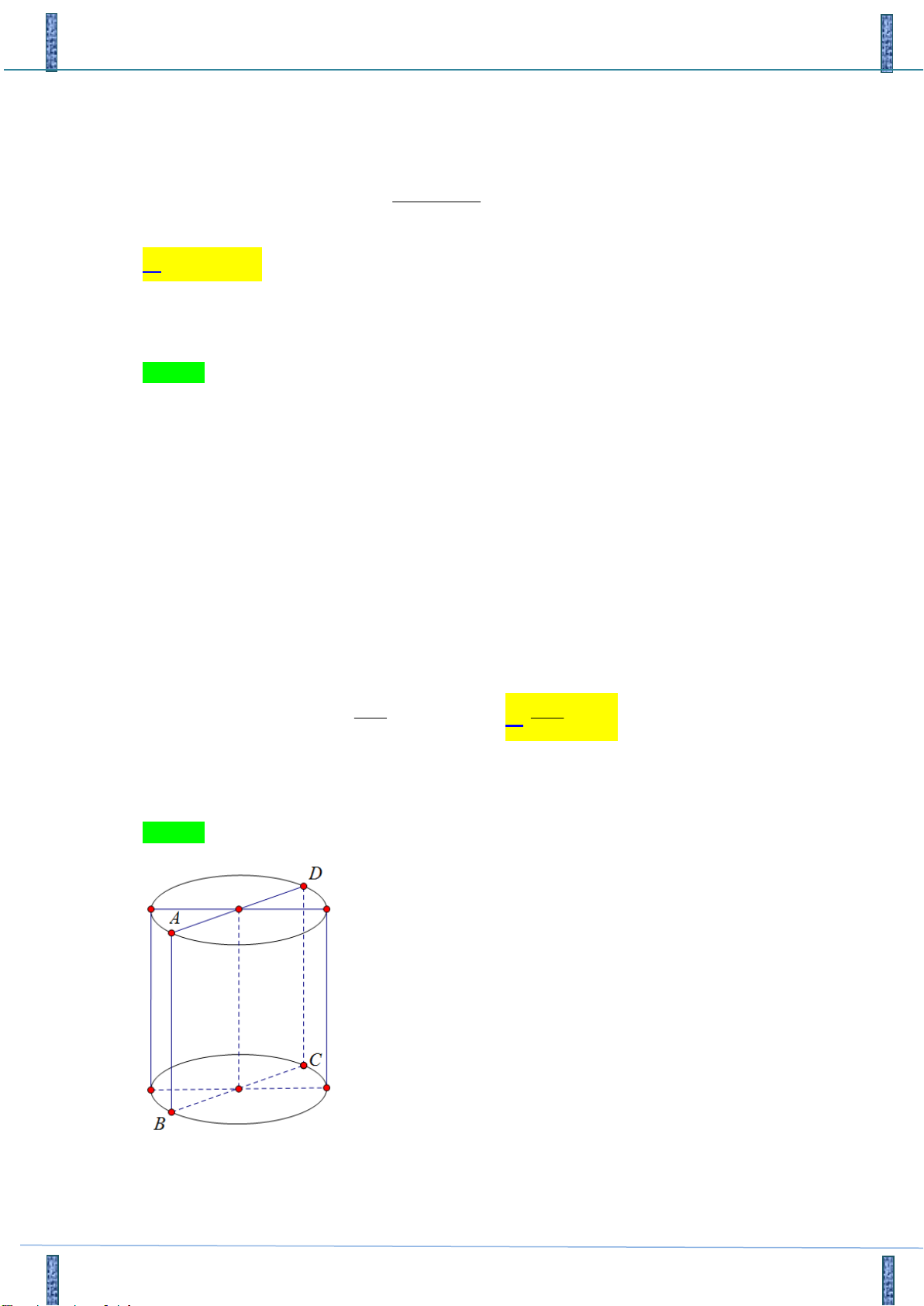
Câu 21: Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 2
30cm và chu vi bằng 26cm . Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của
hình trụ (T). Diện tích toàn phần của (T) là: 23 69 A.   2 23 cm . B.  2 cm . C.  2 cm . D.   2 69 cm . 2 2
Câu 22: Cho log 3  a . Tính log 18 12 24 theo a . 3a 1 3a 1 3a 1 3a 1 A. . B. . C. . D. . 3  a 3  a 3  a 3  a 12   Câu 23: 3 x
Hệ số của số hạng chứa 6
x trong khai triển nhị thức  
 (với x  0 ) là:  x 3  220 220 220  220 A. . B. 6 x . C. 6 x . D. . 729 729 729 729
Câu 24: Khối nón N  có bán kính đáy bằng 3 và diện tích xung quanh bằng 15 . Tính thể tích V của khối nón N A. V  36 B. V  60 C. V  20 D. V  12
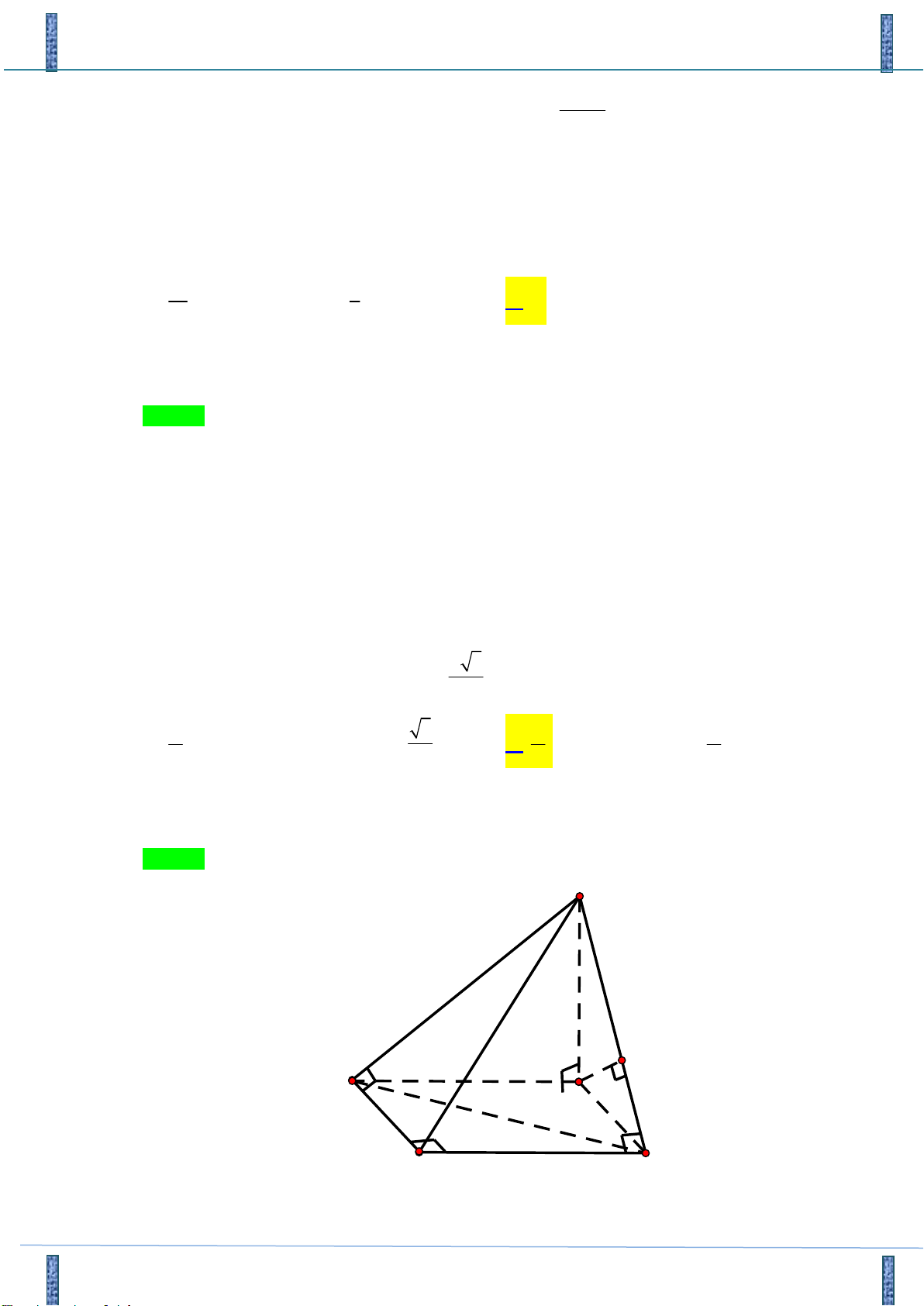
Câu 25: Cho tứ diện ABCD có AB AC, DB DC. Khẳng định nào sau đây là đúng?
A. AB BC
B. CD   ABD
C. BC AD
D. AB  (ABC)      
Câu 26: Cho phương trình 3 sin 2x -  sin x  .   
 Tính tổng các nghiệm thuộc khoảng 0;  của  4   4  phương trình trên. 7 3  A. . B.  . C. . D. . 2 2 4
Câu 27: Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị? 2x  3 A. y . B. 4
y x . x  2 C. 3
y  x x .
D. y x  2 .Câu 28: x
Có bao nhiêu tiếp tuyến của đồ thị hàm số 2 3 y
đi qua giao điểm hai đường tiệm cận? x  2 A. 1. B. Không có. C. Vô số. D. 2.
Câu 29: Trong mặt phẳng tọa độ Oxy cho tam giác ABC có D3;4, E 6; 
1 , F 7;3 lần lượt là trung điểm các cạnh A , B BC,C .
A Tính tổng tung độ của ba đỉnh tam giác ABC. 16 8 A. B. C. 8 D. 16 3 3
Câu 30: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, B A BC  ,
a SAB SCB  90 , 
biết khoảng cách từ A đến mặt phẳng ( a SBC) bằng
3 . Góc giữa SC và mặt phẳng (ABC)là: 2  3   A. . B. arccos . C. . D. . 6 4 3 4 Câu 31: Cho hàm số
có đồ thị C  . Có bao nhiêu điểm A thuộc C  sao cho tiếp tuyến
của Ctại A cắt C tại hai điểm phân biệt M x ; y , N x ; y ( M , N khác A ) thỏa mãn 1 1   2 2
y y  5 x x . 1 2  1 2 A. 1. B. 2 . C. 0 . D. 3 .
Trang 3/6 - Mã đề thi 101
Câu 32: Giả sử đồ thị hàm số 2 4 2 2
y  (m 1)x  2mx m 1 có 3 điểm cực trị là , A , B C mà
x x x . Khi quay tam giác ABC quanh cạnh AC ta được một khối tròn xoay. Giá trị của m để thể A B c
tích của khối tròn xoay đó lớn nhất thuộc khoảng nào trong các khoảng dưới đây: A. (4;6) B. 2; 4 C.  2  ;0 D. (0; 2)
Câu 33: Giải phương trình 8.cos 2 . x sin 2 .
x cos 4x   2.       x   kx   k  32 4 8 8 A.  k  . B.  k  . 3   3   x   kx   k  32 4  8 8       x    kx   k  32 4 16 8 C.  k  . D.  k  . 5   3   x   kx   k  32 4  16 8  Câu 34: m log x 2
Tìm tất cả các giá trị thực của tham số m để hàm số 2 y  nghịch biến trên log x m 1 2 4; .
A. m  2 hoặc m  1.
B. m  2 hoặc m  1.
C. m  2 hoặc m  1. D. m  2.
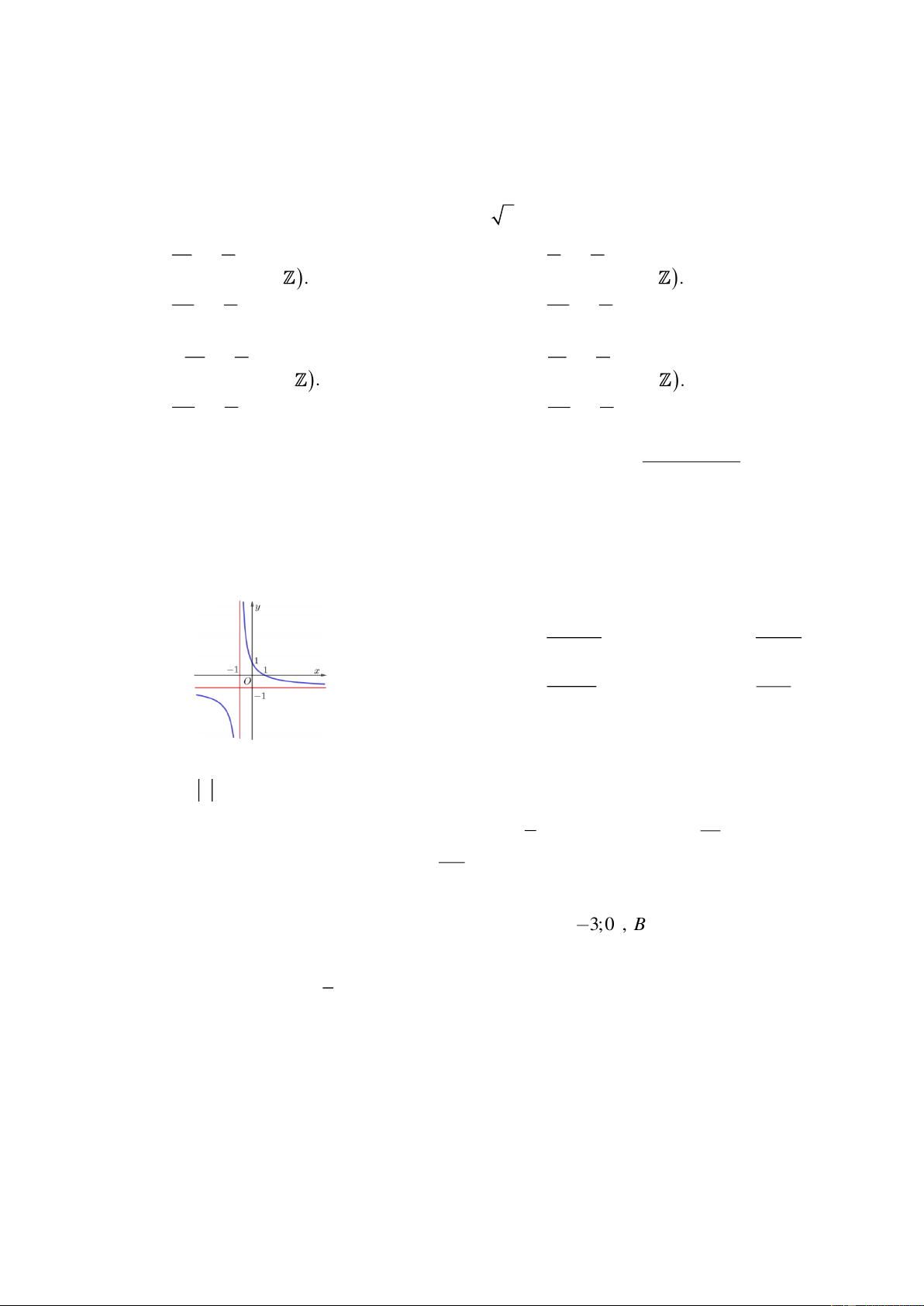
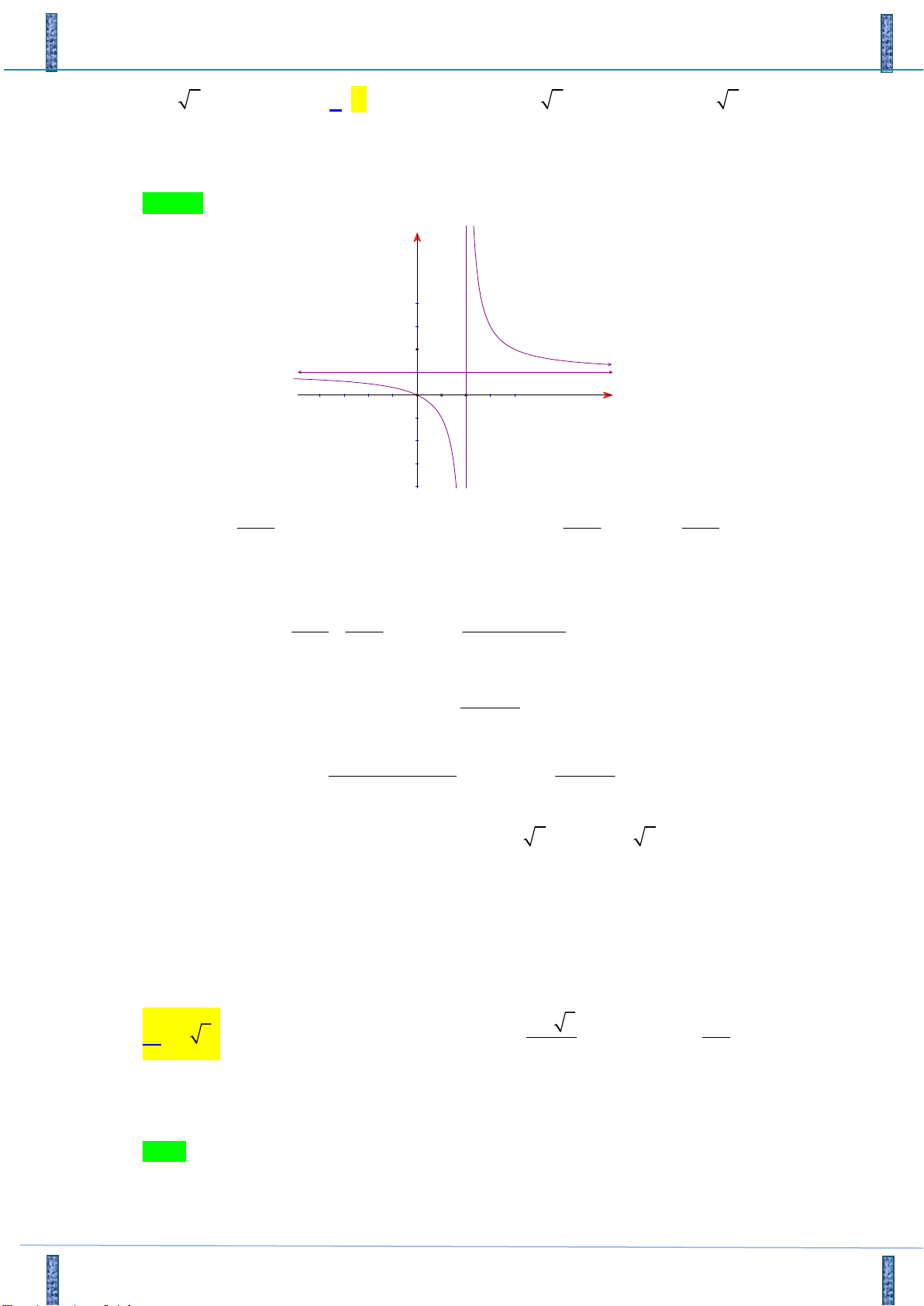
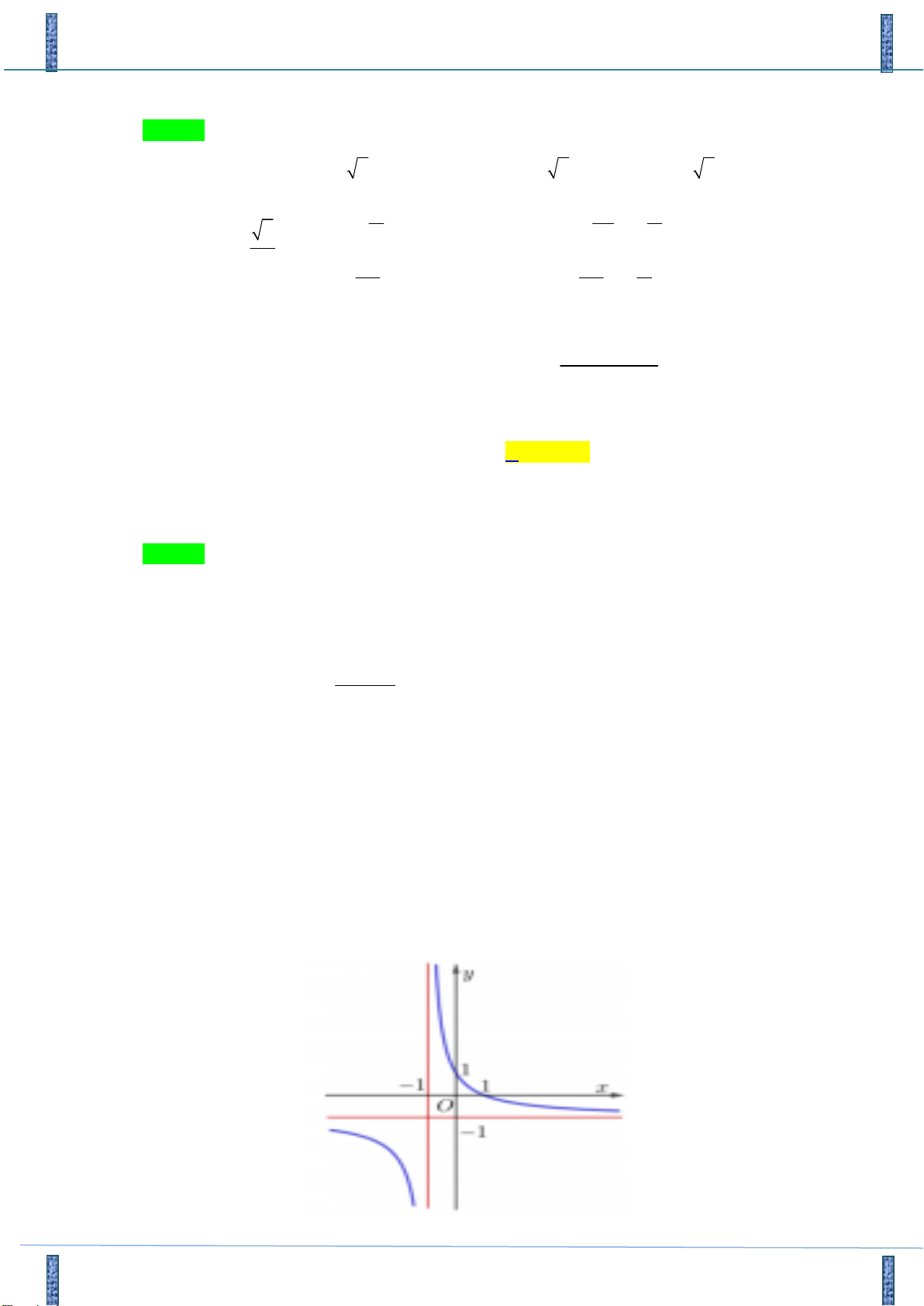
Câu 35: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? 2  x 1 x 1 A. y  y  2x  B. 1 x  1 x  2 x C. y  y  x  D. 1 x  1
Câu 36: Cho hàm số 3 2
y f (x)  x  (2m 1)x  (3  )
m x  2 . Tìm tất cả các giá trị của tham số m để
hàm số y f ( x ) có 3 điểm cực trị. 1 1  A. m  3. B. m  3. C.   . m D. m  3. 2 2
Câu 37: Có bao nhiêu số tự nhiên có 3 chữ số abc sao cho a, b, c là độ dài 3 cạnh của một tam giác cân. A. 45. B. 216. C. 81. D. 165.
Câu 38: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A
3;0 , B 3;0 và C 2; 6 . Gọi H ; a b
là trực tâm của tam giác ABC. Tính 6 . ab 5 A. 10 B. C. 60 D. 6 3
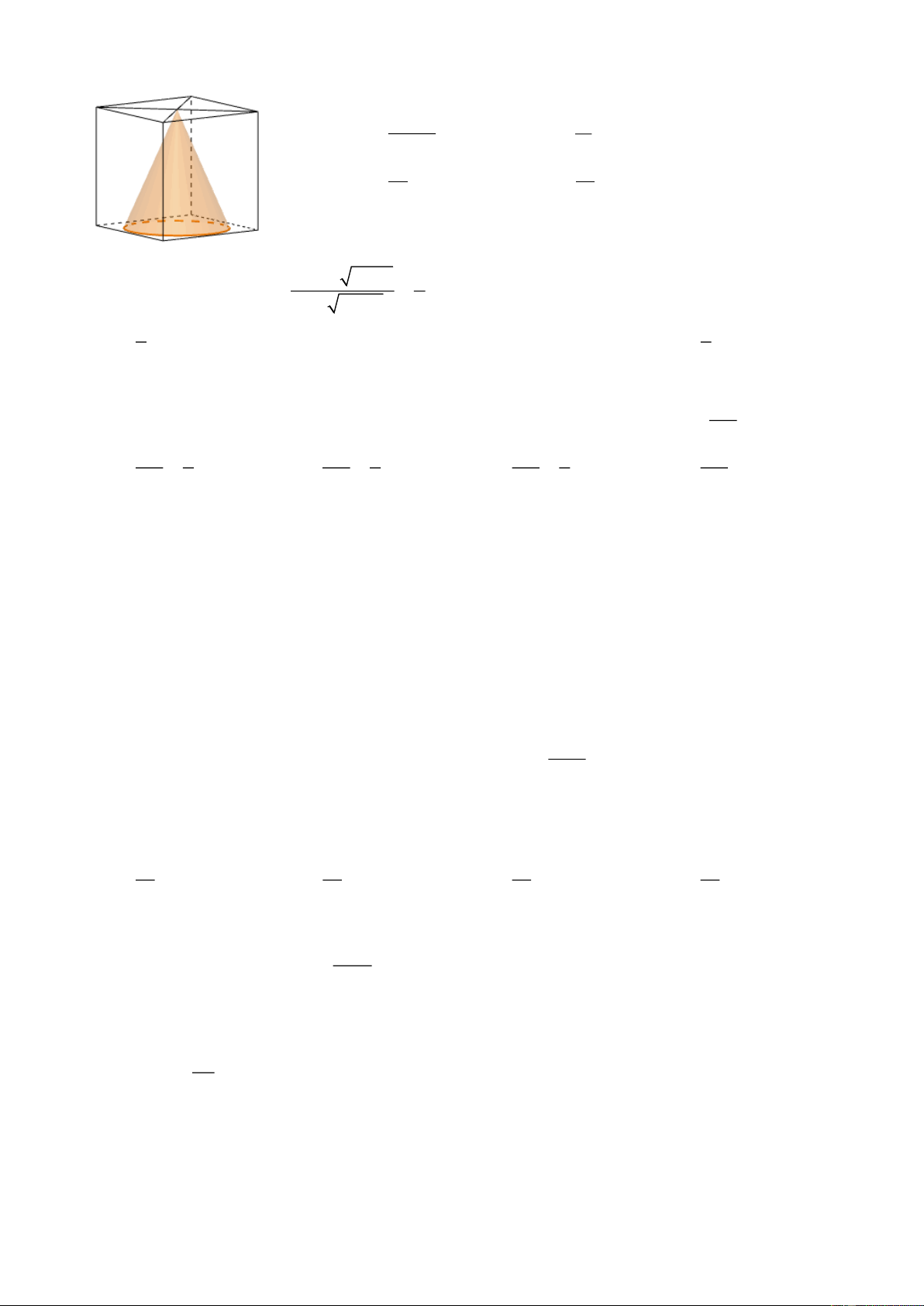
Câu 39: Một chiếc thùng đựng nước có hình của một khối lập phương chứa đầy nước . Đặt vào trong
thùng đó một khối có dạng nón sao cho đỉnh trùng với tâm một mặt của lập phương, đáy khối nón tiếp
xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước trào ra ngoài và lượng nước còn lại ở trong thùng.
Trang 4/6 - Mã đề thi 101  1 A. . B. . 12   11  11 C. . D. 12 12    Câu 40: x 1 5x 1 a Cho giới hạn lim
 (phân số tối giản). Giá trị củaT  2a b là: x 3  x  4x  3 b 1 9 A. . B. -1. C. 10. D. . 9 8
Câu 41: Cho tứ diện ABC .
D Gọi K, L lần lượt là trung điểm của AB và BC, N là điểm thuộc đoạn CD PA
sao cho CN  2N .
D Gọi P là giao điểm của AD với mặt phẳng  KLN . Tính tỷ số . PD PA 1 PA 2 PA 3 PA A.  . B.  . C.  . D.  2. PD 2 PD 3 PD 2 PD
Câu 42: Tìm số nghiệm của phương trình log x  log x 1  2. 2 2   A. 0 B. 1 C. 3 D. 2 Câu 43: Hàm số   2 y ln x  mx  
1 xác định với mọi giá trị của x khi m  2  A. B. m  2 C. 2   m  2 D. m  2 m  2
Câu 44: Trong một lớp có 2n  3 học sinh gồm An, Bình, Chi cùng 2n học sinh khác. Khi xếp tùy ý
các học sinh này vào dãy ghế được đánh số từ 1 đến 2n  3 , mỗi học sinh ngồi một ghế thì xác xuất để
số ghế của An, Bình, Chi theo thứ tự lập thành cấp số cộng là 17 Số học sinh của lớp là: 1155 . A. 27. B. 25. C. 45. D. 35.
Câu 45: Cho một khối lập phương có cạnh bằng .
a Tính theo a thể tích của khối bát diện đều có các
đỉnh là tâm các mặt của khối lập phương. 3 a 3 a 3 a 3 a A. B. C. D. 4 6 12 8
Câu 46: Đồ thị hàm số y f x đối xứng với đồ thị của hàm số x
y a (a  0, a  1) qua điểm I 1  ;1 .  
Giá trị của biểu thức 1 f 2  log  bằng a   2018 
A. 2016 . B. 2016 . C. 2020 . D. 2020 .
Câu 47: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y  sin x  3cos x msin x 1 đồng biến  trên đoạn 3    ;   .  2 
A. m  3 . B. m  0 .
C. m  3 . D. m  0 .
Câu 48: Một cái phễu có dạng hình nón chiều cao của phễu là 30 .
cm Người ta đổ một lượng nước vào
phễu sao cho chiều cao của cột nước trong phễu bằng 15 .
cm (Hình H ). Nếu bịt kín miệng phễu rồi lật 1
ngược phễu lên (hình H ) thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây? 2
Trang 5/6 - Mã đề thi 101 H H 1 2 A. 1,553 (cm). B. 1,306 (cm). C. 1,233 (cm). D. 15 (cm).
Câu 49: Hàm số y  log  x x
4  2  m có tập xác định là thì 2  1 1 1 A. m  B. m  0 C. m  D. m  4 4 4
Câu 50: Cho hình thang vuông ABCD với đường cao AB  2a, các cạnh đáy AD a và BC  3 . a Gọi
M là điểm trên đoạn AC sao cho AM k AC. Tìm k để BM C . D 4 3 1 2 A. . B. . C. . D. . 9 7 3 5 ----------- HẾT ----------
Trang 6/6 - Mã đề thi 101
ĐÁP ÁN CÁC MÃ ĐỀ THI THỬ LẦN 2 KHỐI 12 (2018-2019)- MÔN TOÁN CÂU MÃ 101 MÃ 102 MÃ 103 MÃ 104 MÃ 105 MÃ 106 MÃ 107 MÃ 108 1 A D C B D D A B 2 C D C B B C D C 3 C C D D B B C D 4 D D D A D B A A 5 D A B C C C B A 6 C B C A A A B A 7 C A C C B A D A 8 C A C D D A D D 9 B D A B D A D A 10 C A C D C D C C 11 C B D B C C C A 12 D D C C D A C C 13 C C B B B C D D 14 D C D A A C A B 15 B B A A D A B B 16 B B A A A C A B 17 A A A A A A B B 18 D C D C B B C C 19 C C D D C B C C 20 A A B B B B C B 21 C D C C C C C A 22 B B D D D D B D 23 A A A A C D A C 24 D D C C B B B B 25 C C C B C C B D 26 B B D B B B A C 27 A A B D A C D B 28 B D A C D B C C 29 C C A B B D D B 30 C C C C C C B B 31 B B A B C C C C 32 B B A A C C D D 33 C C A A D D A A 34 D D D D D A B A 35 B B D A B D C C 36 A A A A A A C D 37 D A A A A A D D 38 A A A A D D C C 39 A B D D D D C A 40 C C D D C C A A 41 D D C C C D D D 42 B D C C D D A A 43 C C A A A A D B 44 D B C C B A C C 45 B A A D B B D D 46 B C B B B B D C 47 B B D D B B C C 48 B B C B D C C B 49 D D B A C B A D 50 D D D D D D C C
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
GIẢI C.TIẾT ĐỀ THI THỬ THPTQG CHUYÊN BẮC NINH LẦN 2-2018-2019   Câu 1.
Giá trị lớn nhất của hàm số 3 2
y  2x  3x  1 1 trên đoạn  ;1 .  2    A. max y  4 . B. max y  6 . C. max y  3. D. max y  5 .  1    1   1   1  ;1   ;1  ;1  ;1 2     2     2     2    Lời giải
Tác giả: Bùi Nguyên Phương. Facebook: Bùi Nguyên Phương Chọn A
Tập xác định: D  ! .   Hàm số 3 2
y  2x  3x  1
1 liên tục và có đạo hàm trên đoạn  ;1 .  2    Đạo hàm: 2
y  6x  6x .   1  x  0  ;1   2    Xét 2
y  0  6x  6x  0   .   1  x  1    ;1    2     1  1 Ta có: y
  ; y 0  1  ; y   1  4 .    2  2 Vậy max y  4 .  1   ;1  2   
lethuhang2712@gmail.com Câu 2.
Xét các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau .
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 1 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau. Lời giải
Tác giả : Lê Thị Thu Hằng, FB: Lê Hằng Chọn C D1 C1 A B 1 1 D C A B
“Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau” và mệnh đề “Hai
mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau” là mệnh đề
sai, ví dụ trong hình lập phương trên ta có (C B BC) và D B BD 1 1  cùng vuông góc với 1 1
(ABCD) nhưng 2 mặt phẳng đó lại cắt nhau.
“Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau” là
mệnh đề sai ví dụ như trong hình lập phương trên ta có A B và C B cùng vuông góc với B B 1 1 1 1 1
nhưng A B C B 1 1 1 1
“Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau” là mệnh đề đúng .
Tuandel2009@gmail.com
Câu 3. Một hình trụ có bán kính đáy r=a,độ dài đường sinh l=2a.Diện tích toàn phần của hình trụ này là: A. 2 2 a . B. 2 4 a . C. 2 6 a . D. 2 5 a . Lời giải
Tác giả : Trần Minh Tuấn Chọn C 2 2
S  2S S  2 a  2.
a 2a  6 a ,chọn C tp d xq
huonghieptb@gmail.com
Câu 4. Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó A.1. B. 2. C. Không có. D. Vô số. Lời giải
Họ và tên tác giả : Đào Thị Hương, FB: Hương Đào
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 2 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 Chọn D
Có vô số phép tịnh tiến biến một đường thẳng thành chính nó. Đó là các phép tịnh tiến có véc
tơ tịnh tiến là véc tơ không hoặc véc tơ tịnh tiến là véc tơ chỉ phương của đường thẳng đó.
Nguyendac1080@gmail.com Câu 5.
Tập nghiệm của bất phương trình 32x-1>27 là: A. (3;  1 ) . B. ( ;  1 ) . C. ( ; ) . D. (2; ) . 3 2 Lời giải
Tác giả :Nguyễn Văn Đắc, FB: Đắc Nguyễn Chọn D 32x-1>27 2 x 1  3  3
 3  2x 1  3  x  2
Vậy tập nghiệm của bất phương trình là (2; )
locleduc10@gmail.com
Câu 6. Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực ! ? . x  2 x
A. y  log x . B. y C. y  .
D. y  log  2 2x 1 . 1      3   e  2 4 Lời giải
Tác giả :Lê Đức Lộc, FB: Lê Đức Lộc Chọn C  2 x  2 Hàm số y
là hàm số mũ, có cơ số 0  a   1nên hàm sốnghịch biến trên tập số thực    e e R .
nongdansanhdieu.tk@gmail.com Câu 7.
Cho hàm số f có đạo hàm trên khoảng I . Xét các mệnh đề sau:
(I). Nếu f ' x  0, x
  I thì hàm số nghịch biến trên I .
(II). Nếu f ' x  0, x
  I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số
nghịch biến trên I .
(III). Nếu f ' x  0, x
  I thì hàm số nghịch biến trên khoảng I .
(IV). Nếu f ' x  0, x
  I và f 'x  0 tại vô số điểm trên I thì hàm số không thể nghịch biến trên khoảng I .
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai? A.
II và IV đúng, còn III sai.
B. I,II,III và IV đúng.
C.I và II đúng, còn III và IV sai.
D.I,II và III đúng, còn IV sai. Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 3 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Tác giả : Nguyễn Tuấn Đạt, FB: Nguyễn Đạt Chọn C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I
hientam112@gmail.com Câu 8.
Một nhóm có 10 người, cần chọn ra ban đại diện gồm 3 người. Số cách chọn là: A. 240. 3 B. A . 3 10 C. C . 360. 10 D. Lời giải
Họ và tên: Bùi Thị Thu Hiền- Fb Hiền Tấm Chọn C
+ Số cách chọn ra 3 người vào ban đại diện trong 10 người là: 3
C (không phân biệt thứ tự). 10 Chọn C
Quachthuy.tranphu@gmail.com.
Câu 9. Trong mặt phẳng tọa độ Oxy cho bốn điểm A3;-5,B-3;3,C -1;-2,D 5;-10. Hỏi  1  G
;-3 là trọng tâm của tam giác nào dưới đây?  3    A. ABC . B. BCD . C. ACD . D. ABD . Lờigiải
Tácgiả:Quách Phương Thúy,FB:Phương Thúy Chọn B  
Ta thấy BC  2; 5  ,BD  8; 1
 3 nên chúng không cùng phương B,C,D là 3 đỉnh của một tam giác.
x x x    B C D 3 1 5 1    Mặt khác, ta lại có 3 3 3
y y y    B C D 3 2 10   3   3 3  1  Vậy G  ; 3
 là trọng tâm của tam giác BCD 3   
xuantoan204@gmail.com
Câu 10. Tập xác định của hàm số y   x  15 1 là: A. 0; . B. 1; . C. 1; . D. ! . Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 4 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Tác giả : Bùi Xuân Toàn, FB: Toan Bui Chọn C
Phương pháp: Hàm số y x
với không nguyên xác định khi x  0 .
Điều kiện xác định của hàm số y   x  15
1 là x 1  0 hay x  1.
Vậy tập xác định: D  1; .
hanhnguyentracnghiemonline@gmail.com
Câu 11. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = tan x .
B. y = sin x .
C. y = cos x .
D. y = cot x . Lời giải
Tác giả : Nguyễn Thị Ngọc Hạnh, FB: Nguyễn Hạnh Chọn C
Hàm số y = tan x, y = sin x, y = cot x là các hàm số lẻ.
Hàm số y = cos x là hàm số chẵn
Mar.nang@gmail.com
Câu 12. Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số 3 2
y x  3x  2 . Mệnh đề nào dưới đây đúng
A. d có hệ số góc dương.
B. d song song với đường thẳng x  3 .
C. d có hệ số góc âm.
D. d song song với đường thẳng y  3 . Lời giải
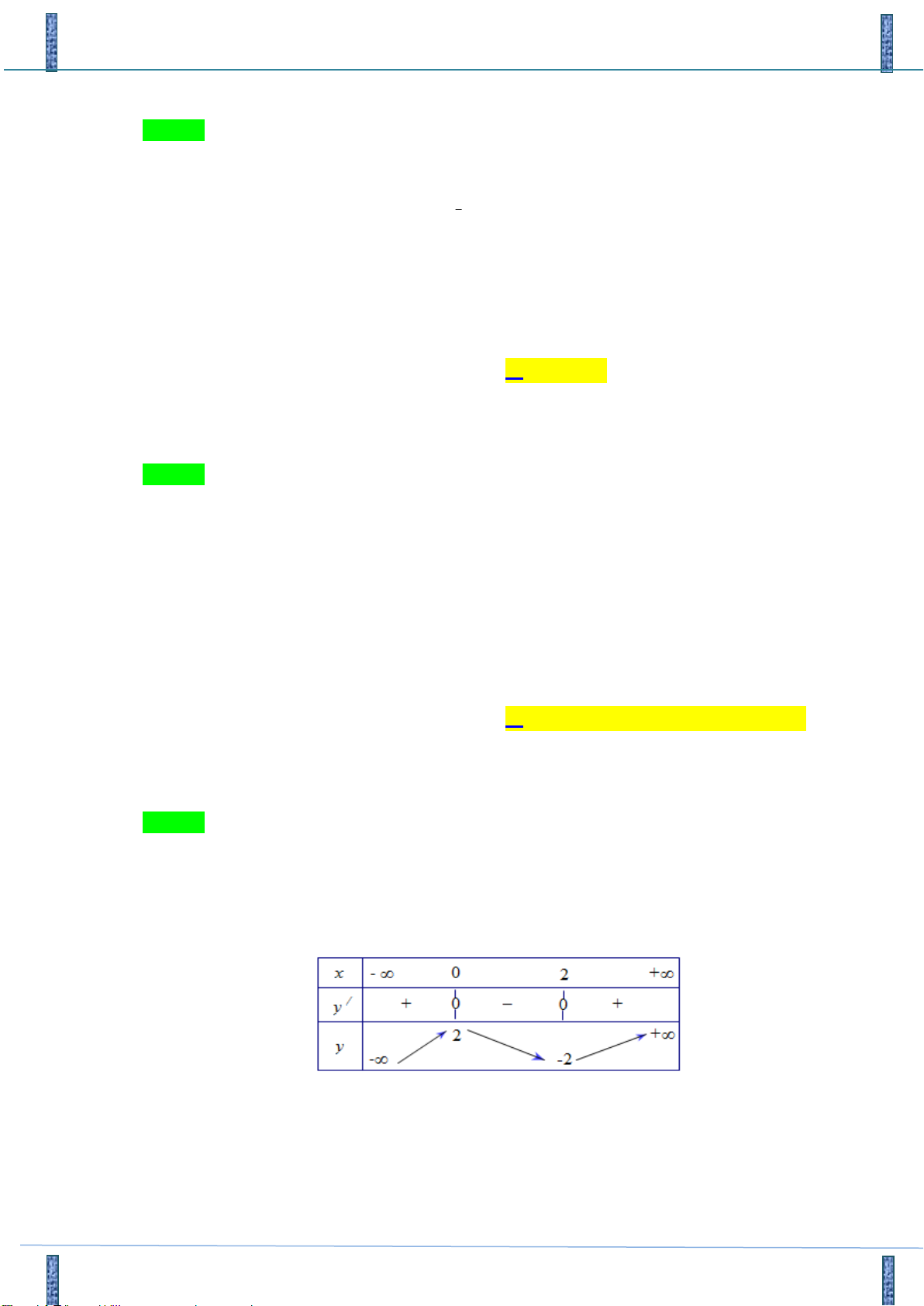
Tác giả : Lê Đình Năng, FB: Lê Năng Chọn D
x  0  y  2 Ta có: 2
y '  3x  6x . y '  0  x  2 y  2 Bảng biến thiên
Từ bảng biến thiên ta suy ra đồ thị hàm số có điểm cực đại là 0;2
Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm 0;2 là
y  0 x  0  2  y  2 d
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 5 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Do đó d song song với đường thẳng y  3.
Trắc nghiệm: Hàm số đã cho có đạo hàm tại mọi điểm và tại điểm cực trị có y '  0 nên tiếp
tuyến d của đồ thị hàm số tại điểm cực đại (hoặc tại điểm cực tiểu) là đường thẳng song song
trục hoặc trùng Ox, từ đó Chọn D.
duyphuongdng@gmail.com
Câu 13. Hình lập phương có mấy mặt đối xứng? A. 5. B. 6. C. 9. D. 10. Lời giải
Tác giả: Đinh Thị Duy Phương, FB: Đinh Thị Duy Phương Chọn D
Nguyenvandieupt@gmail.com
Câu 14. Trong các dãy số sau, dãy nào là cấp số cộng: n A. 1 u 3n  2 . B. u  . C. 2 u n  5 2 1 . D. u  . n n n 1 n n 3 Lời giải
Tác giả: Nguyễn Văn Diệu, FB:dieuptnguyen Chọn D
Ta có dãy u là cấp số cộng khi * uu d , n
  ! với d là hằng số. n n 1  n
Bằng cách tính 3 số hạng đầu của các dãy số ta dự đoán đáp án D. 5n   1  2 5n  2 5 Xét hiệu * uu    , n   ! . n 1  n 3 3 3
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 6 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 5n  2 Vậy dãy u  là cấp số cộng. n 3
(nguyenthithutrang215@gmail.com) u   5
Câu 15. Cho dãy số u 20 n  1 :  . Số
là số hạng thứ mấy trong dãy? uu nn 1 n A. 5 . B. 6 . C. 9 . D. 10 . Lời giải
Tác giả: Nguyễn Thị Thu Trang, FB: Trang Nguyễn Chọn B Cách 1:
u  5,u  6,u  8,u  11,u  15,u  20 1 2 3 4 5 6
Vậy số 20 là số hạng thứ 6 . Cách 2:
Dựa vào công thức truy hồi ta có u  5 1 u  5 1 2 u  5 1 2 3 u  5 1 2  3 4 ..... n n   1
u  5 1 2  ...  n 1  5  n 2 nn   1 n 6 2    20  5  n! 
*  n n  30  0  2  n  5(lo¹i)
Vậy 20 là số hạng thứ 6 .
Cách 3: Sử dụng máy tính CASIO fx – 570VN PLUS 1 SHIFT STO A 5 SHIFT STO B
Ghi vào màn hình C = B + A: A = A + 1: B = C
Ấn CALC và lặp lại phím =
Ta tìm được số 20 là số hạng thứ 6
thuyhung8587@gmail.com x
Câu 16. A và B là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số y  . Khi đó độ dài đoạn x  2
AB ngắn nhất bằng
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 7 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 A. 4 2 . B. 4 . C. 2 2 . D. 2 2 . Lời giải
Tác giả: Cấn Việt Hưng, FB: Viet Hung Chọn B y 1 O 1 2 x xa   b  Hàm số y
có đồ thị C như hình vẽ. Gọi A ; a và B ; b là hai điểm     x  2  a  2   b  2 
thuộc hai nhánh của C a  2  b .   b a   b a
Ta có: AB b  ; a     b  ; a  .  b 2 a 2   
b 22 a      b a
Áp dụng BĐT Côsi ta có: b    a  2 2 2  . 4 2 b a 64
Suy ra: AB  b a2 2   
 b a2  16
b    a 2 2 2  2   b a
AB  4 . Dấu bằng xảy ra khi và chỉ khi a  2  2 và b  2  2 . Vậy AB  4 . min
(chamtt.toan@gmail.com)
Câu 17. Cho hình lăng trụ đều ABC.A' B 'C ' . Biết mặt phẳng  A' BC tạo với mặt phẳng  ABC một góc 0
30 và tam giác A' BC có diện tích bằng 2
8a . Tính thể tích khối lăng trụ ABC.A' B 'C '. 3 8a 3 3 8a A. 3 8a 3 . B. 3 8a . C. . D. . 3 3 Lời giải
Tác giả :Trần Thị Chăm - HHA, FB: Cham Tran Chọn A
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 8 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Gọi M là trung điểm của BC .
Chứng minh được BC   AA'M  . Do đó góc giữa hai mặt phẳng  A' BC và mặt phẳng  ABC là góc ! 0 A' MA  30 . Đặt AB x Cách 1: x 3 AM
Tam giác ABC đều nên AM   A'M   x 0 2 cos 30 1 1 2 2 2 S
 .A'M.BC x  8a x  4a S  4a 3 A'BC 2 2 ABC AA' 0
 sin 30  AA'  2a A' M Vậy 3 VAA'.S  8a 3
ABC.A'B 'C '. ABC Cách 2:
Tam giác ABC là hình chiếu của tam giác A' BC lên mặt phẳng ABC 0 2  SS .cos30  4a 3 ABC A'BC
x  4a AM  2a 3 AA' 0
 tan 30  AA'  2a AM 3 VAA'.S  8a 3
ABC.A'B 'C '. ABC
thinhvanlamha@gmail.com
Câu18. Cho hìnhchóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm thuộc đoạn SB ( M khác S và B ). Mặtphẳng  ADM  cắt hình
chóp S.ABCD theo thiết diện là A.Hình bình hành. B.Tam giác. C.Hình chữ nhật. D.Hình thang. Lờigiải
Tácgiả :NguyễnVănThịnh, FB: ThịnhNguyễnVăn
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 9 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 Chọn D
Ta có M là một điểm thuộc đoạn SB với M khác S và B .
M  ADM  SBC 
AD   ADM  Suy ra 
  ADM SBC  Mx // BC // AD .
BC  SBC   AD // BC
Gọi N Mx SC thì  ADM  cắt hình chóp S.ABCD theo thiết diện là tứ giác AMND . Vì
MN // AD và MN với AD không bằng nhau nên tứ giác AMND là hình thang.
nhuthanh3112@gmail.com
Câu 19. Hàm số nào sau đây có đồ thị như hình bên? A. 4 2
y  x  4x  3 . B. 4 2
y  x  2x  3.
C. y  x  2 2 2 1.
D. y  x  2 2 2 1. Lời giải
Tác giả : Trần Như Thanh Nhã, FB: Nhã Trần Như Thanh Chọn C
Dựa vào hình dạng của đồ thị hàm số 4 2
y ax bx csuy ra hệ số a > 0  loại A, B.
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 10 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Và hàm số có 3 điểm cực trị  a.b < 0  y   x  2 2 2 1
kimoanh0102@gmail.com 1
Câu 20. Tìm tập xác định của hàm số y  . log 5 x 2   A.  ;   5 \   4 . B. 5; . C.  ;   5 . D. 5;   . Lời giải
Tác giả :Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn A
Điều kiện xác định của hàm số là 5 x  0  x  5 x  5      . log 5  x  0 5    x  1 x  4 2  
Vậy tập xác định của hàm số là D   ;   5 \   4 .
Hungvn1985@gmail.com
Câu 21. Cắt hình trụ T  bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 30 2
cm và chu vi bằng 26 cm . Biết chiều dài của hình chữ nhật lớn hơn đường kính
mặt đáy của hình trụ T  . Diện tích toàn phần của T  là: 23 69
A. 232 cm  . B.  2 cm  . C.  2 cm  . D.  2 69 cm  . 2 2 Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn C Gọi ,
h r lần lượt là đường cao và bán kính đáy của hình trụ T  . Thiết diện của mặt phẳng và
hình trụ T  là hình chữ nhật ABCD . Khi đó theo giả thiết ta có
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 11 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019    h  2rh  2rh  2rh  2r     S  . h 2r  30  hr 15
 h 13 2r
 h 13 2r ABCD    2 C
 2(h  2r)  26 h 2r 13    r r     
r   h l ABCD 2 15 15 0 5 3( )   3
r   h 10(TM )  2 Vậy .
ngoquoctuanspt@gmail.com
Câu 22. Cho log 3  a . Tính log 18 theo a . 12 24 3a 1 3a 1 3a 1 3a 1 A. . B. . C. . D. . 3  a 3  a 3  a 3  a Lời giải
Tác giả : Ngô Quốc Tuấn, FB: Quốc Tuấn Chọn B log 3 log 3 log 3 log 3 2a Ta có: a  log 3 2   2  2   log 3  . 12 log 12 log  2 2 .3 log 2  log 3 2  log 3 2 1 a 2  2 2 2  2 2 2 2a  log 18 log  2 2.3 1 2. 2  12log 3 3a 1 Ta có: 2 log 18   2  1 a   . 24 log 24 log  3 2 .3 3  log 3 2a 3  a 2  2 2 3  1a 3a 1 Vậy log 18  . 24 3  a
Thuylinh133c3@gmail.com 12  3 x
Câu 23. Hệ số của số hạng chứa 6
x trong khai triển nhị thức  (với x  0 ) là :    x 3  2  20 220 2  20 220 A. . B. 6 x . C. 6 x . D. . 729 729 729 729 Lời giải
Tác giả : Nguyễn Thùy Linh, FB: Nguyễn Thùy Linh Chọn A 12  3 x
Số hạng tổng quát trong khai triển  là:    x 3  12  3 k k   x T C   C      k k k 122k 2k 1  2 1 3 x
k  ! , k  12 . 12 12    x   3 
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 12 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 T chứa 6
x  2k 12  6  k  9.
Vậy hệ số cần tìm là :  2  20 C 1  3  12  9 9 6 . 729
Cohangxom1991@gmail.com
Câu 24. Khối nón (N ) có bán kính đáy bằng 3 diện tích xung quanh bằng 15. Tính thể tích V của khối nón (N ) .
A. V  36.
B. V  60.
C. V  20.
D. V  12. Lời giải
Tác giả : Phạm Văn Huy, FB: Đời Dòng Chọn D S xq 15
Ta có S  rl l    5. xq  r 3 Chiều cao 2 2
h l r  25  9  4. 1 2 1 2
V  r h .3 .4  12. 3 3
trichinhsp@gmail.com
Câu 25. Cho tứ diện ABCD có AB AC, DB DC . Khẳng định nào sau đây là đúng?
A. AB BC .
B. CD   ABD.
C. BC AD .
D. AB   ABC  . Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn trí Chính A B D I C Chọn C
Gọi I là trung điểm BC.
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 13 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Có AB AC , IB IC . Suy ra AI là trung trực của BC . Nên BC AI
Tương tự BC DI
Suy ra BC   AID . Suy ra BC AD . Chọn C
nguyentuanblog1010@gmail.com  3
Câu 26. Cho phương trình sin 2x   sin x
. Tính tổng các nghiệm thuộc khoảng 0; của      4   4  phương trình trên. 7 A. . B. 3 . C. . D. . 2 2 4 Lời giải
Tác giả : Phạm Chí Tuân, FB: Tuân Chí Phạm Chọn B 3 2x   x   k2
x k2 3      Ta có: 4 4 sin 2x sin x           
2k  !  .  4   4  3x    k 2x
x   k2  6 3  4 4
+ Xét x k2k !  . 1
Do 0  x  0  k2   k  0 . Vì k  ! nên không có giá trị k . 2 2 + Xét x   kk !  . 6 3 2 1 5
Do 0  x  0   k
   k  . Vì k ! nên có hai giá trị k là: k  0;k 1. 6 3 4 4
 Với k  0  x  . 6  5
Với k  1  x  . 6
Do đó trên khoảng 0; phương trình đã cho có hai nghiệm x  5 và x  . 6 6 5
Vậy tổng các nghiệm của phương trình đã cho trong khoảng 0; là:   . 6 6
tuluc0201@gmail.com
Câu 27. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị? 2x  3 A. y  . B. 4 y x . C. 3
y  x x .
D. y x  2 . x  2 Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 14 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Tác giả : Võ Tự Lực, FB: Võ Tự Lực Chọn A. 2x  3
+ Hàm số y x2
Tập xác định: D   ;  2    2  ; . 7 Có y '   0 x
  D  hàm số luôn đồng biến trên từng khoảng xác định  hàm số x  22 không có cực trị.
Các hàm số khác dễ dàng chứng minh được y’ có nghiệm và đổi dấu qua các nghiệm. Riêng
hàm số cuối y’ không xác định tại -2 nhưng hàm số xác định trên R và y’ đổi dấu qua -2 do đó
có hàm số có điểm cực trị x = -2.
(tien.vuviet@yahoo.com) 2x  3
Câu 28. Có bao nhiêu tiếp tuyến của đồ thị y
đi qua giao điểm của hai đường tiệm cận? x  2 A. 1. B. Không có. C. Vô số. D. 2 . Lời giải
Tác giả : Vũ Việt Tiến, FB: Vũ Việt Tiến Chọn B d
Đồ thị hàm số nhận đường thẳng x    2  làm tiệm cận đứng. c a
Đồ thị hàm số nhận đường thẳng y   2 làm tiệm cận ngang. c Vậy I  2
 ;2 là giao điểm của hai đường tiệm cận. TXĐ: D  ! 7 y '  2 (x  2) 2x  3
Gọi tiếp tuyến tại M x ; y y  0
0  của đồ thị hàm số có dạng: x  2   7 2x 3
: y y ' x .(x x )  y 0  : y  .(x x )  0  hay 0 0 2 0 (x  2) x  2 0 0 7 2x  3 Vì  đi qua I  2  ;2 0  2  .( 2   x )  2 0 (x  2) x  2 0 0 7  2x  3 7  2x  3 0 0  2  .(x  2)   2   2 0 (x  2) x  2 (x  2) x  2 0 0 0 0 2x 10 0  2   4  1
 0 , phương trình vô nghiệm. x  2 0
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 15 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 2x  3
Vậy không tồn tại tiếp tuyến nào của đồ thị hàm số y
mà đi qua giao điểm của hai x  2 tiệm cận.
tien.vuviet@yahoo.com
Câu 29. Trong mặt phẳng tọa độ Oxy cho tam giác ABC có D 3;4, E 6; 
1 , F 7;3 lần lượt là trung
điểm các cạnh AB, BC,CA .Tính tổng tung độ ba đỉnh của tam giác ABC . 16 8 A. . B. . C. 8 . D.16 . 3 3 Lời giải
Tác giả: Vũ Việt Tiến, FB: Vũ Việt Tiến Chọn C
y y  2y  2.4  8 A B D
Ta có y y  2y  2.3  6  2 y y y     A C FA B C  8 6 2 16
y y  2y  2.1 2  B C E
y y y  8. Chọn C. A B C
Nguyentinh050690@gmail.com.
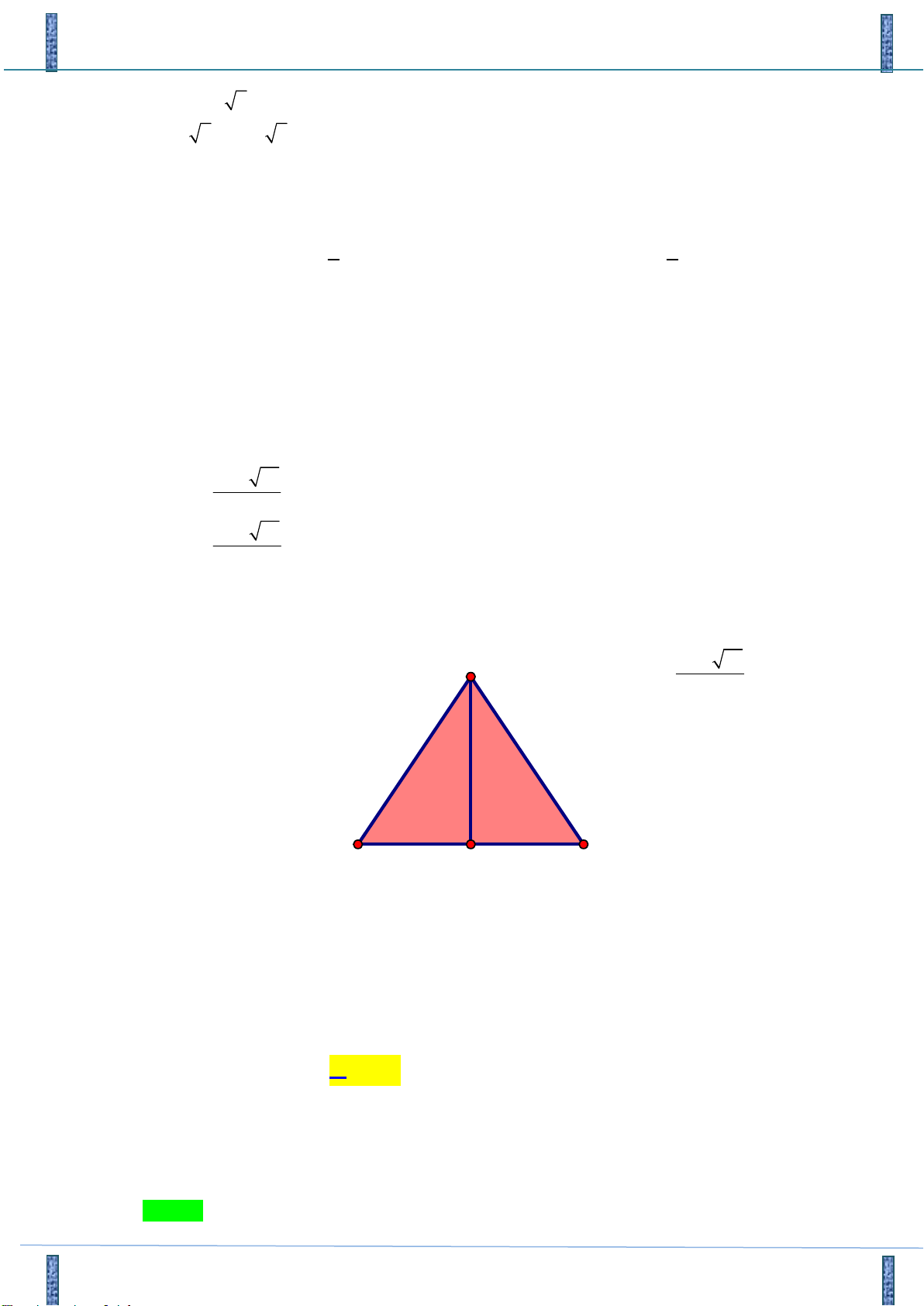
Câu 30. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, ! ! 0
BA BC a, SAB SCB  90 , a 3
biết khoảng cách từ A đến SBC bằng
. Góc giữa SC và mặt phẳng  ABC là: 2 3 A. . B. a rccos . C. . D. . 6 4 3 4 Lời giải
Tác giả: Nguyễn Tình, FB: Gia Sư Toàn Tâm. Chọn C S H A D C B
Gọi D là hình chiếu vuông góc của S lên  ABC .
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 16 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
H là hình chiếu vuông góc của D lên SC . AB SA Khi đó: 
AB  SAD  AB AD . AB SDBC SC
BC  SDC  BC DCBC SD
ABCD là hình vuông và CD a . a 3
Ta có: AD | BC AD | SBC   dd
DH DH  .
A,SBC
D,SBC 2
Vì DC là hình chiếu vuông góc của SC lên mặt phẳng  ABCD nên ! SCD là góc giữa
đường thẳng SC và  ABC . ! DH 3 ! sin SCD    SCD DC 2 3
lientoanc3@gmail.com 1 Câu 31. Cho hàm số 4 2
y x  3x có đồ thị (C) . Có bao nhiêu điểm A thuộc (C) sao cho tiếp tyến của 4
(C) tại A cắt (C) tại hai điểm phân biệt M (x ; y ) , N (x ; y ) (M , N khác A ) thỏa mãn 1 1 2 2
y y  5(x x ) 1 2 1 2 A. 1. B. 2 . C. 0 . D. 3. Lờigiải
Tác giả: Nguyễn Thị Kim Liên; FB: Kim Liên Chọn B 3
y '  x  6x 1 Gọi 4 2 (
A x ; x  3x ) là tọa độ tiếp điểm của tiếp tuyến tại A. Phương trình tiếp tuyến tại A là 0 0 0 4
đường thẳng (d) có phương trình: 1 3 4 2
y  (x  6x )(x x )  x  3x 0 0 0 0 0 4
Phương trình hoành độ giao điểm của (d) và (C) là: 1 1 3 4 2 4 2
(x  6x )(x x )  x  3x x  3x 2 2 2
 (x x ) (x  2x x  3x 12)  0 0 0 0 0 0 4 4 0 0 0 x x  0 0   2
x  2x x  3x 12  0 (2)  0 0
(d) cắt (C) tại hai điểm phân biệt khác A khi và chỉ chi phương trình (2) có hai nghiệm phân biệt khác x0
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 17 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019x   2 0   (3)  6  x  6  0
Khi đó, phương trình (2) có hai nghiệm phân biệt x , x và (d) cắt (C) tại hai điểm phân biệt 1 2
M (x ; y ) , N (x ; y ) trong đó: 1 1 2 2 1 1 3 4 2
y  (x  6x )(x x )  x  3x 3 4 2
y  (x  6x )(x x )  x  3x 1 0 0 1 0 0 0 4 2 0 0 2 0 0 0 4 3
y y  (x  6x )(x x ) 1 2 0 0 1 2 Từ giả thiết ta suy ra: 3
(x  6x )(x x )  5(x x ) 3
x  6x  5 (Vì x x ) 0 0 1 2 1 2 0 0 1 2  x  1  0   1   21  x  0  2   1   21 x  0  2
Kết hợp với điều kiện
(3) có hai giá trị x thỏa mãn 0 yêu cầu bài toán là x  1  0  B 1    21 x  0  2 r A I C h
cunconsieuquay1408@gmail.com
Câu 32. Giả sử đồ thị hàm số y   2 m   4 2 2
1 x  2mx m 1 có 3 điểm cực trị là , A B,C mà
x x x . Khi quay tam giác ABC quanh cạnh AC ta được một khối tròn xoay. Giá trị của A B C
m để thể tích của khối tròn xoay đó lớn nhất thuộc khoảng nào trong các khoảng dưới đây: A. 4;6 . B. 2;4 . C.  2  ;0 . D. 0;2 . Lời giải
Tác giả: Nguyễn Thị ThanMai, FB: Thanh Mai Nguyen Chọn B
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 18 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 2 3 2 2
y  4(m 1)x  4mx  4x (m 1)x - m   x  0 + 2 2
y  0  4x (m 1)x - m  0       mx   (m  0) 2  m 1
+ Với m  0 thì đồ thị hàm số có 3 điểm cực trị (với x x x ) là: A B C 2 m m 2 2 m m ( A  ; -  m 1) ; 2 B(0; m 1) ; 2 C( ; -  m 1) . 2 2 m 1 m 1 2 2 m 1 m 1 + Quay A
BC quanh AC thì được khối tròn xoay có thể tích là: 1 2 2 9  m  2 2 2 2 m 2 m
V  2. . r h  BI .IC   .  . 3 3 2 2 3  m 1 m  1 3 m  5 2 1 9 m
+ Xét hàm số f (x)  m  5 2 1 8 2 m (9 - m ) Có: f '(x)  ; f (
x)  0  m  3 (m  0) . m  6 2 1 Ta có BBT: x 0 3  f x –   0  max f x 0 0
Vậy thể tích cần tìm lớn nhất khi m  3 .
ptpthuyedu@gmail.com
Câu 33. Giải phương trình 8.cos 2 . x sin 2 .
x cos 4x   2  x   kx   kA. 32 4  (k  8 8 ! ) . B.  (k  ! ) . 3  3 x   k   x   k  32 4  8 8  x    kx   kC. 32 4  (k  16 8 ! ) . D.  (k  ! ) . 5  3 x   k   x   k  32 4  16 8 Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 19 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Tác giả : Phạm Thị Phương Thúy, FB: Thuy phạm Chọn C 8.cos 2 . x sin 2 .
x cos 4x   2  4.sin 4 .
x cos 4x   2  2.sin 8x   2  8x    k2 x    k 2   4 32 4  sin 8x     (k  ! )   (k  ! ) 2 5 5 8  x   k2x   k  4  32 4
tcdung.math@gmail.com m log x  2
Câu 34. Tìm tất cả các giá trị thực của tham số m để hàm số 2 y
nghịch biến trên 4; log x m 1 2 A. m  2  hoặc m  1 . B. m  2  hoặc m  1. C. m  2  hoặc m  1. D. m  2  . Lời giải
Tác giả : Trần Công Dũng, FB: trancong.dung.948 Chọn D
Đặt t  log x . 2
Ta có x 4;  t 2;. mt  2
Hàm số được viết lại y  (1). t m 1
Vì t  log x đồng biến trên 0; nên yêu cầu bài toán  (1) nghịch biến trên 2; 2   
mm   m 2 1  2  0   
 m 1  m  2  . m 1 2  m  1
mp01100207@gmail.com
Câu 35. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ?
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 20 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 2  x 1 x 1 x  2 x A. y  . B. y  . C. y  . D. y  . 2x 1 x 1 x 1 x 1 Lời giải
Tác giả : Minh Anh Phuc, FB: Minh Anh Phuc Chọn B
Từ đồ thị của hàm số đã cho ta có:
Tiệm cận đứng của đồ thị hàm số là đường thằng có phương trình x  1  .
Tiệm cận ngang của đồ thị hàm số là đường thằng có phương trình y  1  .
Đồ thị hàm số đi qua các điểm 1;0 và 0;  1 . x 1
Suy ra hàm số cần tìm là y . x 1
Đangvanquanggb1@gmail.com Câu 36. Cho hàm số 3
y x   m   2 2
1 x  3 mx  2 . Tìm tất cả các giá trị của tham số m để hàm số
y f x  có 3 điểm cực trị. A. m  3 . B. m  1 3 . C.   1 m 3.
D.   m  3 . 2 2 Lời giải
Tácgiả :Đặng Văn Quang, FB: DangQuang Chọn A Hàm số 3
y x   m   2 2
1 x  3 mx  2 TXĐ: ! 2
y  3x  22m  
1 x  3 m
Hàm số y f x  có ba điểm cực trị khi và chỉ khi phương trình y  0 có hai nghiệm x , x 1 2
thỏa mãn x  0  x . 1 2
Trường hợp 1: Phương trình y  0 có hai nghiệm x  0  x  3 3 m  0  m  3 1 2  
Trường hợp 2: Phương trình y  0 có hai nghiệm x  0  x 1 2
Có y0  0  m  3 x  0 Với m  3 thì 2
y  3x 14 ; x y  0   14 (thỏa mãn) x   0  3
Vậy với m  3 thì hàm số y f x  có ba điểm cực trị.
Tranquocan1980@gmail.com
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 21 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Câu 37. Có bao nhiêu số tự nhiên có 3 chữ số abc sao cho a,b,c là độ dài 3 cạnh của một tam giác cân. A.45. B.216. C.81. D.165. Lờigiải
Tácgiả :Trần Quốc An, FB: TranQuocAn Chọn D TH1: a, ,
b c là độ dài 3 cạnh của một tam giác đều.
Trường hợp này có 9 số thỏa mãn yêu cầu bài toán. TH2 : a, ,
b c là độ dài 3 cạnh của một tam giác cân và không đều.
Không làm mất tính tổng quát, giả sử a b .
*) a b c
+ a b  2  c  1.
+ a b  3  c  1, 2.
+ a b  4  c  1, 2,3. ………..
+ a b  9  c  1, 2,3,...,8
 Có : 1 2  3  .. 8  36 số thỏa bài toán.
*) a b c c
Do a b c   a  . c 2 9
+ c  9   a  9  a  5,6,7,8. 2
+ c  8  4  a  8  a  5,6,7. 7
+ c  7   a  7  a  4,5,6 2
+ c  6  3  a  6  a  4,5. 5
+ c  5   a  5  a  3, 4. 2
+ c  4  2  a  4  a  3 3
+ c  3   a  3  a  2. 2
+ c  2,1 không có a tương ứng.
 Có : 4  3  3  2  2 11 16 số thỏa bài toán.
 Trong trường hợp a b c , có : 36 16  52 số thỏa mãn.
Tương tự, mỗi trường hợp b c a , c a b đều có 52 số thỏa mãn.
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 22 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Theo quy tắc cộng ta có: 9  52.3  165 số thỏa mãn yêu cầu bài toán bài toán.
Nguyenvandiep1980@gmail.com
Câu 38. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A 3
;0 ,B3;0,C 2;6 . Gọi H a;b là
trực tâm của tam giác ABC . Tính 6ab 5 A. 10. B. . C. 60. D. 6. 3 Lời giải
Tác giả : Nguyễn Văn Điệp, FB: Nguyễn Văn Điệp Chọn A A H B C 
Đường thẳng AH đi qua A 3
;0 và nhận BC   1
;6 làm véctơ pháp tuyến. Suy ra
phương trình đường thẳng AH là: x  6y  3  0 . 
Đường thẳng BH đi qua B 3;0 và nhận AC  5;6 làm véctơ pháp tuyến. Suy ra phương
trình đường thẳng BH là: 5x  6y 15  0 .
x  6y  3  0  5 
Ta có H AH BH  Tọa độ H là nghiệm của hệ   H 2; . 5
x  6y 15  0    6  5
Do đó a  2;b   6ab  10 . 6
lanthangqn@gmail.com
Câu 39. Một chiếc thùng chứa đầy nước có hình một khối lập phương. Đặt vào trong thùng đó một khối
nón sao cho đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với
các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước trào ra ngoài và lượng nước còn lại ở trong thùng.
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 23 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 1 11 A. . B. . C. . D. . 12  11 12 12 Lời giải
Tác giả : Nguyễn Thị Lan, FB: Nguyen Thi Lan Chọn A
Coi khối lập phương có cạnh 1. Thể tích khối lập phường là V  1 .
Từ giả thiết ta suy ra khối nón có chiều cao h  1
1, bán kính đáy r  . 2
Thể tích lượng nước trào ra ngoài là thể tích V của khối nón. 1 1 1 1 Ta có: 2
V  r h . .1  . 1 3 3 4 12 12 
Thể tích lượng nước còn lại trong thùng là: V V V  1  . 2 1 12 12 V Do đó: 1  . V 12  2
Damvanthuong1205@gmail.com
x 1 5x 1 a
Câu 40. Cho giới hạn lim
 (phân số tối giản). Giá trị của T  2a b là x3 x  4x  3 b 1 9 A. . B. 1  . C. 10 . D. . 9 8 Lời giải
Tác giả : Đàm Văn Thượng, FB: Thượng Đàm Chọn C x   x
 2x 3xx 4x3 1 5 1  lim  lim x3 x3 x  4x  3
 2x 4x3x1 5x1
x x  4x 3 3.3 3 9  lim   .
x3  x  
1 x 1 5x 1 2.4  4 8
Vậy T  2a b  10 .
Email: buichithanh1987@gmail.com
Câu 41. Cho tứ diện ABCD . Gọi K, L lần lượt là trung điểm của AB và BC . N là điểm thuộc đoạn PA
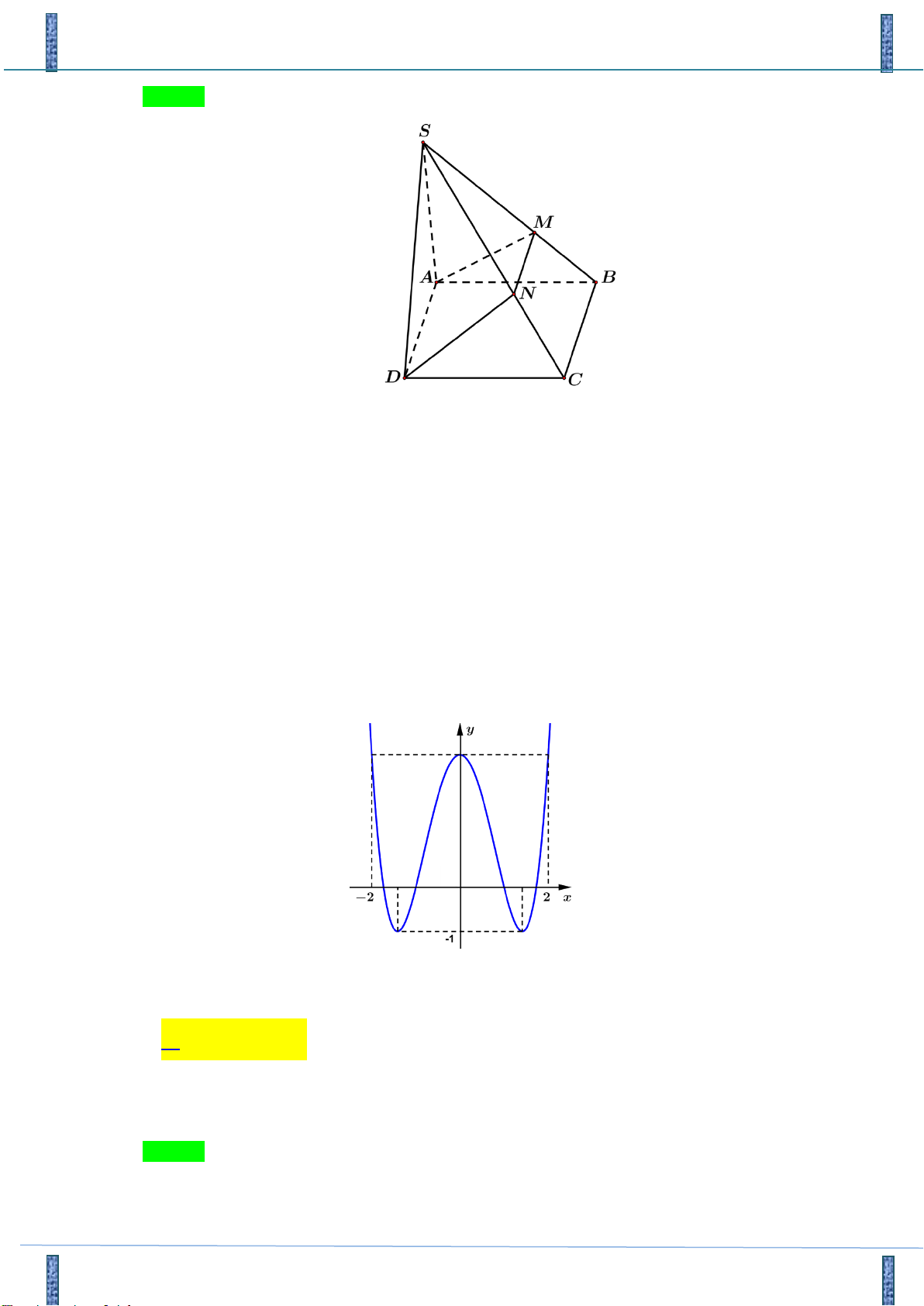
CD sao cho CN  2ND . Gọi P là giao điểm của AD với mặt phẳng (KLN) . Tính tỉ số PD PA 1 PA PA PA A.  2 . B.  3 . C.  . D.  2 . PD 2 PD 3 PD 2 PD
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 24 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 Lời giải
GV giải : Bùi Chí Thanh Facebook: Thanhbui Chọn D A K P B D I N L C
Giả sử LN BD I . Nối K với I cắt AD tại P Suy ra (KLN)  AD P PA NC
Ta có: KL / / AC PN / / AC Suy ra:   2 PD ND
ptpthuyedu@gmail.com
Câu 42. Tìm số nghiệm của phương trình log x  log (x  1)  2 2 2 A. 0. B. 1. C. 3. D. 2. Lời giải
Tác giả : Phạm Thị Phương Thúy, FB: Thuy pham Chọn B
Điều kiện: x  1
Ta có: log x  log (x  1)  2 2 2 2
 log [x(x 1)]  2  x(x 1)  4  x x  4  0 2  1  17 x  2   1 17 x   2 1 17
Đối chiếu với điều kiện ta được nghiệm của phương trình là x  . 2
Vnhtk2017@gmail.com
Câu 43. Hàm số y   2
ln x mx  
1 xác định với mọi giá trị của x khi.
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 25 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019m  2  A. . B. m  2 . C. 2   m  2 . D. m  2 .  m  2 Lời giải
Tác giả : Phạm Văn Nghiệp, FB: Phạm Văn Nghiệp Chọn C Yêu cầu bài toán  2
x mx 1  0 , x   ! 2  m  4  0  2   m  2 .
ngoletao@gmail.com
Câu 44. Trong một lớp có 2n  3 học sinh gồm An, Bình, Chi cùng 2n học sinh khác. Khi xếp tùy ý
các học sinh này vào một dãy ghế được đánh số từ 1 đến 2n  3 , mỗi học sinh ngồi một ghế thì 17
xác suất để số ghế của An, Bình, Chi theo thứ tự lập thành một cấp số cộng là . Số học sinh 1155 của lớp là A. 27 . B. 25 . C. 45 . D. 35 . Lời giải
Tác giả : Ngô Lê Tạo, FB: Ngô Lê Tạo Chọn D
Số cách các xếp học sinh vào ghế là 2n  3!.
Nhận xét rằng nếu ba số tự nhiên a, ,
b c lập thành một cấp số cộng thì a c  2b nên a c là
một số chẵn. Như vậy a, c phải cùng chẵn hoặc cùng lẻ.
Từ 1 đến 2n  3 có n 1 số chẵn và n  2 số lẻ.
Muốn có một cách xếp học sinh thỏa số ghế của An, Bình, Chi theo thứ tự lập thành một cấp số
cộng ta sẽ tiến hành như sau:
Bước 1: chọn hai ghế có số thứ tự cùng chẵn hoặc cùng lẻ rồi xếp An và Chi vào, sau đó xếp
Bình vào ghế chính giữa. Bước này có 2 2 A A cách. n 1  n2
Bước 2: xếp chỗ cho 2n học sinh còn lại. Bước này có 2n! cách.
Như vậy số cách xếp thỏa yêu cầu này là  2 2 A A . 2n ! n 1  n2    . Ta có phương trình  2 2 A A . 2n !     n 1  n2    17 nn  1
n 1n 2 17     2n  3! 1155
2n  12n  22n   3 1155 2
 68n 1019n 1104  0 n 16   69 n   (loaïi)  68
Vậy số học sinh của lớp là 35 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 26 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
tanbaobg@gmail.com
Câu 45. Cho một hình lập phương có cạnh bằng a . Tính theo a thể tích của khối bát diện đều có các đỉnh
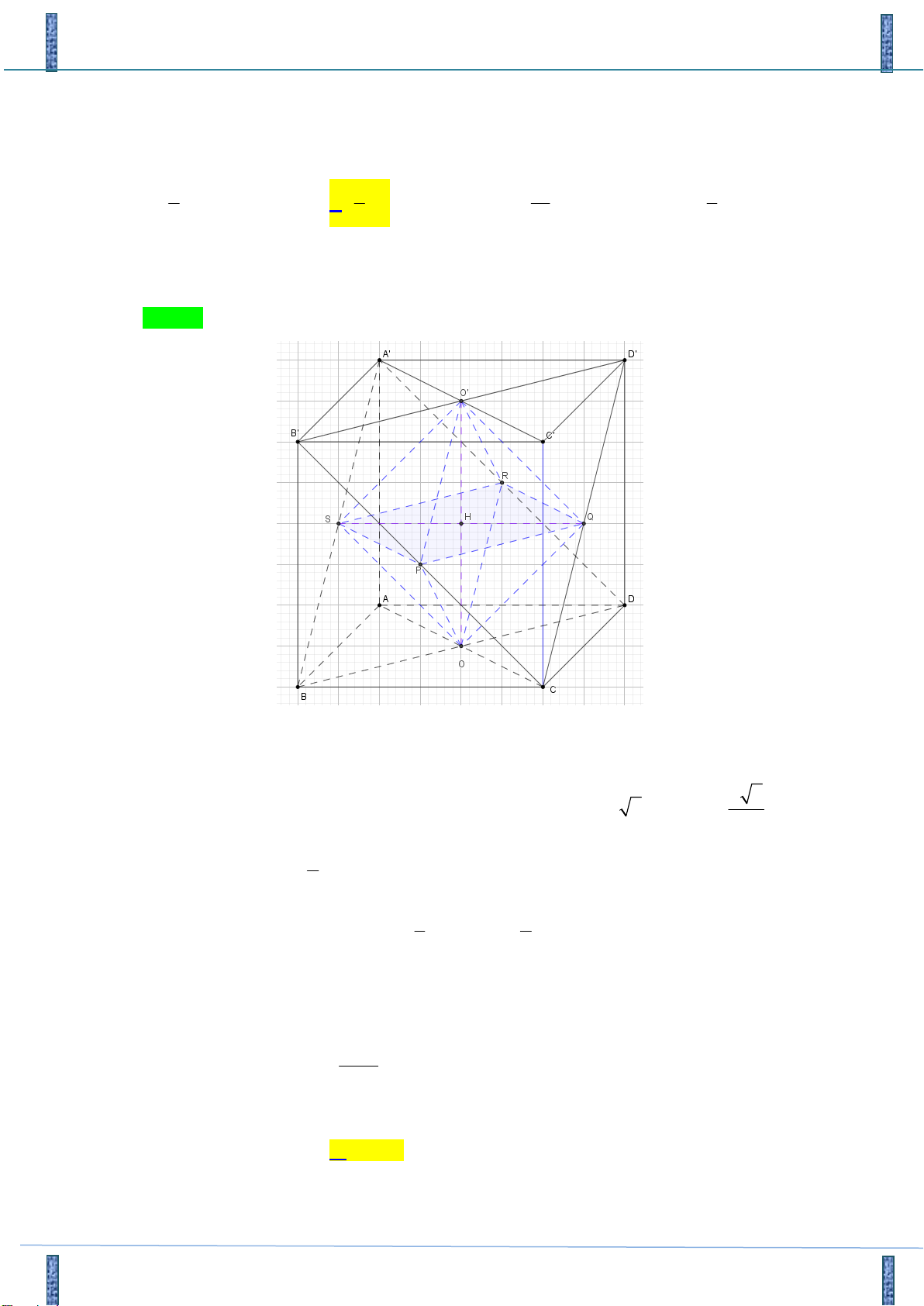
là tâm các mặt của hình lập phương. 1 1 1 1 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 6 12 8 Lời giải
Tác giả : Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo Chọn B
Giả sử hình lập phương ABC . D AB CD
  có cạnh bằng a và tâm các mặt là P,Q, R, S,O,O như hình vẽ. a 2
Ta có PQ là đường trung bình của tam giác đều B C
D cạnh a 2 nên PQ  . 2 1 Do đó 2 2 S
PQ a và OO  a . PQRS 2 1 1
Vậy thể tích bát diện cần tìm là 3 V S
.OO  a (đvtt). 3 PQRS 6
builoiyka@gmail.com
Câu 46. Đồ thị hàm số y f x đối xứng với đồ thị hàm số x
y a a  0,a  
1 qua điểm I 1;  1 . Giá trị  1 
của biểu thức f 2  log bằng  a   2018  A. 2016 . B. 2016  . C. 2020 . D. 2020  . Lờigiải
Tác giả : Bùi Thị Lợi, FB: Loi Bui
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 27 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 Chọn B
Gọi C là đồ thị hàm số x
y a ; C
y f x
1  là đồ thị hàm số .  1   1  M 2  log ; yC
y f 2  log a M   1 .    2018  M a  2018   1 
Gọi N đối xứng với M qua I 1;  1  N  log ; 2  y .  a   2018 M   1  Do đồ thị CCI 1;  1 N  log ; 2  yCa M    1  đối xứng qua nên .  2018  1 log N C 2018  2 ay a log 2018  2 ay a
 2  y  2018  y  2016  . M M M M  1  Vậy f 2  log  2016  .  a   2018 
nguyentuyetle77@gmail.com
Câu 47. Tìm tất cả các giá trị của tham số m để hàm số 3 2
y  sin x  3cos x msin x 1 đồng biến trên 3   ;  2    A. m  3 . B. m  0 . C. m  3 . D. m  0 . Lời giải
Tác giả : NguyễnTuyết Lê, FB: Nguyen Tuyet Le Chọn B Ta có: 3 2
y f (x)  sin x  3sin x msin x  4 (1) . 3
Đặt t  sin x , do x    ;  t 1;0.  2    Hàm số (1) trở thành 3 2
y g(t)  t  3t mt  4(2) . 3
Hàm số (1) đồng biến trên   ;
khi và chỉ khi hàm số (2) nghịch biến trên   1  ;0 2    ,
g (t)  0, t   1  ;0 ( ,
g (t)  0 tại hữu hạn điểm). Hàm số 3 2
y g(t)  t  3t mt  4 trên  1  ;0, ta có , 2
g (t)  3t  6t m . Suy ra: , g (t)  0, t   1  ;0 2
 3t  6t m  0, t   1  ;0 2
 3t  6t  , m t   1  ;0 Xét hàm số 2
y h(t)  3t  6t trên đoạn  1  ;0.
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 28 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 Ta có '
h (t)  6t  6  0, t   1
 ;0  h(t) đồng biến trên  1  ;0. max ℎ(𝑡) = ℎ(0) = 0 [ ‒ 1;0] Tức , g (t)  0, t   1
 ;0  max ℎ(𝑡) ≤ 𝑚 ∀𝑡 ∈ [ ‒ 1;0] .Do đó có m  0 . [ ‒ 1;0] 3
Hàm số (1) đồng biến trên   ;
khi và chỉ khi m 0; .Chọn đáp án B  2   
luuquihien@gmail.com
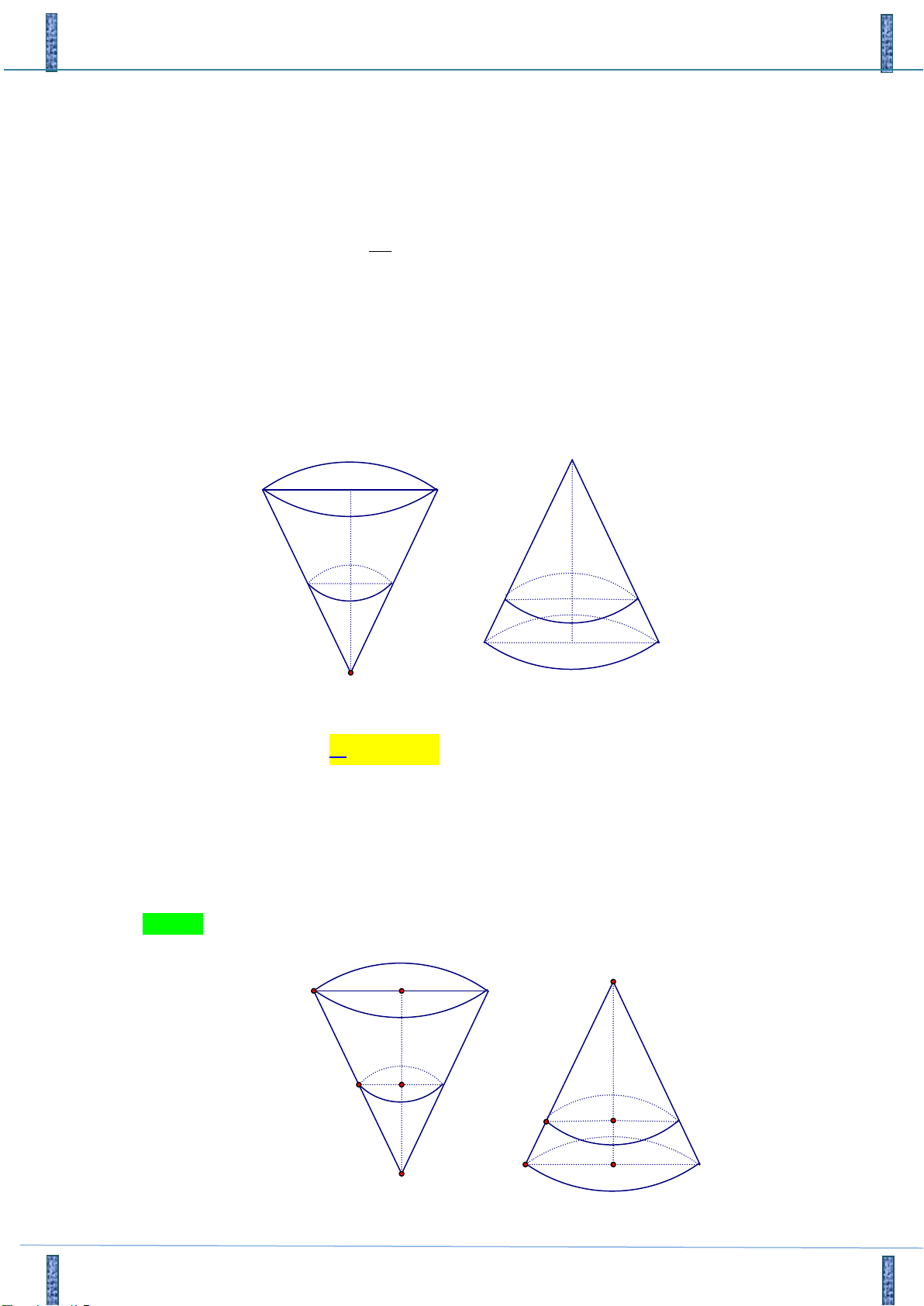
Câu 48. Một cái phễu có dạng hình nón chiều cao của phễu là 30cm . Người ta đổ một lượng nước vào
phễu sao cho chiều cao của cột nước trong phễu bằng 15cm (hình H ). Nếu bịt kín miệng phễu 1
rồi lật ngược phễu lên ( hình H ) thì chiều cao của cột nước trong phễu gần với giá trị nào sau 2 đây ? H2 H1
A. 1,553cm .
B. 1,306cm .
C. 1, 233cmD. 15cm . Lời giải
Tác giả : Lưu Quí Hiền, FB: lưu quí hiền
Phản biện: Nguyễn Đức Duẩn Chọn B E A O N M P Q A O E
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 29 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Phễu có dạng hình nón, gọi E là đỉnh, đáy là đường tròn tâm O , bán kính OA
chiều cao OE  30cm .
Gọi V là thể tích của khối nón có đỉnh E , đáy là đường tròn tâm O , bán kính OA . 1 Ta có 2 2
V .OA .OE  10OA 3
Gọi M là trung điểm của đoạn OE , N là trung điểm của đoạn EA .Khi đổ nước vào phễu
chiều cao của cột nước là EM  15cm .
Gọi V là thể tích của khối nón có đỉnh E , đáy là đường tròn tâm M , bán kính MN . 1  1 5 1 Thể tích nước là 2 2 2
V .MN .EM  5.MN .OA V V 1 3 4 1 8
Khi bịt kín miệng phễu rồi lật ngược phễu lên, chiều cao của cột nước là OP .
Gọi V là thể tích của khối nón có đỉnh E , đáy là đường tròn tâm P , bán kính PQ 2 1 2 7 V 7 .PQ .PE 7 2 PQ .PE 7 Ta có 2
V V V V   3     1 2   2 1 8 V 8 1 2 8
.OA .OE OA .OE 8 3 Ta có P
EQ vuông tại P và O
EA vuông tại O có ! ! OEA PEQ PEQ và OPQ PE EA đồng dạng   OA OE 3  PE  7 3 PE 7 3 OE OP 7 Do đó   1          OE  8 OE 2 OE 2 3  7  3    7
OP OE 1    301   1,306cm 2      2  
phunghang10ph5s@gmail.com
Câu 49. Hàm số  log 4x  2x ym ! 2 
 có tập xác định là thì 1 A. m  . B. m  1 0 . C. m  1 . D. m  . 4 4 4 Lời giải
Tác giả : Phùng Hằng, FB: Hằng Phùng
Phản biện: Nguyễn Đức Duẩn Chọn D
Điều kiện xác định: 4x  2x m  0
Hàm số đã cho có tập xác định là !  4x  2x
 0,   !   4x   2x m x m , x   ! (*) Đặt  2x t ,t  0
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 30 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019 Khi đó (*) trở thành 2 m t   t, t
  0  m  max f (t) với 2
f (t)  t
  t, t  0 0;
Ta có: f 't  2
t 1, f t 1 '  0  t  2
Bảng biến thiên của hàm số 2
f (t)  t
  t, t  0 : 1 t 0  2 f 't + 0 - 1 4 f t 0  1
Từ BBT ta thấy max f (t)  1
đạt được khi t  0; 4 2 1
Vậy m  max f t  m  0; 4
Duanquy@gmail.com
Câu 50. Cho hình thang vuông ABCD có đường cao AB  2a , các cạnh đáy AD a và BC  3a . Gọi  
M là điểm trên đoạn AC sao cho AM k AC . Tìm k để BM CD 4 3 1 2 A. . B. . C. . D. . 9 7 3 5 Lời giải
Tác giả : Nguyễn Đức Duẩn Chọn D
Chọn hệ trục tọa độ như hình vẽ sao cho gốc tọa độ trùng với điểm B , điểm A thuộc trục Oy
và điểm C thuộc trục Ox .
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 31 Mã đề 101
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Thi Thử Chuyên Bắc Ninh Lần 2-2018-2019
Theo bài ra ta có B(0;0), (
A 0; 2), C(3;0), D(1; 2)   x  3t Khi đó AC  (3; 2
 ) . Phương trình tham số của đường thẳng AC là  ,t ! y  2  2t   
Gọi M AC M (3t; 2  2t) . Ta có BM  (3t; 2  2t) và DC  (2; 2  )    6 6  Để BM  2
DC thì BM .DC  0  6t  4  4t  0  t   M ;   5  5 5    6 4   52  Khi đó AM  ;  AM  và   AC  3; 2    AC  13  5 5  5     AM 52 2
Vì AM k AC và AM , AC cùng chiều  k    AC 5 13 5
Hãy tham gia STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 32 Mã đề 101
Document Outline

  • [toanmath.com] - Đề thi khảo sát Toán 12 năm 2018 – 2019 trường THPT chuyên Bắc Ninh lần 2.pdf
    • 101
    • ĐÁP ÁN CÁC MÃ ĐỀ
  • Giải Chi Tiết Đề Thi thử THPTQG CHUYÊN BẮC NINH Lần 2-2018-2019-Fi.pdf