Đề thi kì 1 Toán 10 năm 2020 – 2021 trường THPT Năng khiếu TDTT Bình Chánh – TP HCM
Giới thiệu đến thầy, cô và các bạn học sinh Đề thi kì 1 Toán 10 năm học 2020 – 2021 trường THPT Năng khiếu TDTT huyện Bình Chánh, thành phố Hồ Chí Minh có đáp án và lời giải chi tiết, mời bạn đọc đón xem
23
12 lượt tải
Tải xuống
sO
GIAO DIJC VA DAO TO TP HO CHI MIN}I
T
'4
C.
,/TRLIiNG
(muc
IQC Pfl 1HO
RANG XHIE
TDTT
J•{. INN
CHANH
T NANG KHIEU TDTT H.BC
KIEM TRA HQC K I — NAM HQC 2020-202 1
MON: TOAN HOC
—
KHOI 10
Thô'i gian lam bài : 90 phuit
oE
CH!NH THUC
Câu 1:
(1,5
diem)
Kháo sat sir bin thiên và
ye
d thj cüa ham
so:
y = x
2
+ 4x —
3
Câu
2:
(0,75
diem)
TIm h s
a,
b
cüa Parabol
(P): y
= ax
2
+ bx
— 4, bit
(P)
di qua
diem A(-1; —7)
và
B(2;
8)
Câu
3: (1,5
dim)
Giãi các phucing trinh sau:
a) I
7
x+
6
1=I
3
x
-2
1
Câu
4: (0,75
dim)
Giãi h phuong trInh sau:
3x = 6
2x+y = 5
x+y+z=6
Câu
5:
(1,0
dim)
TIm
m
d phuo'ng trinh x
2
+ (2m + 1)x +
m
2
— 3m — 4 = 0 cO 2
nghim x
1
; x
2
thOa man: x + x = 37.
Câu 6: (1,0 diem)
Trong mt phng to d Oxy cho ba dim
A(-1;
3);
B(2;
1);
C(3;
5).
a)
Xác djnh tQa d cüa vecto
b)
Xác djnh to d trçng tam G cüa
MBC
Câu
7: (2,5
dim)
Trong mit phng tot d Oxy cho
t
= (1; —5), = (-2; —7).
a)
Tfnh tIch vô hincng .
b
-
-
'
-4
b)
Phan tich vecto
c
= (7; —1) theo 2 vecto a va
b.
c)
TIm
m
d vecto = (2m
2
+ 8m — 2;
m)
vuông góc vâi vecto
LEL
Câu 8: (1,0 dim)
Tim giá trj nhó nhtt (GTNN) cüa ham s:
x
12
1
Y 3+4x
1
,VOIX
>.
•
..Hêt...
Ho ten HS:
S báo danh:
Ló'p:
b)V3x2_9x+1=x_2
IflJ
c vA DAO
TiO TP. HCM
NANG KHIEU TDTT H.BC
ThU HOC PHO 1HUC
HANG KHE WIT
H. 8H CHANH
IJAP AN DE KIEM TRA CUOI HQC Kl I
MON: TOAN
10-
NAM HOC: 2020 — 2021
•-
Cth
7
Pap an
Diem
Câu 1
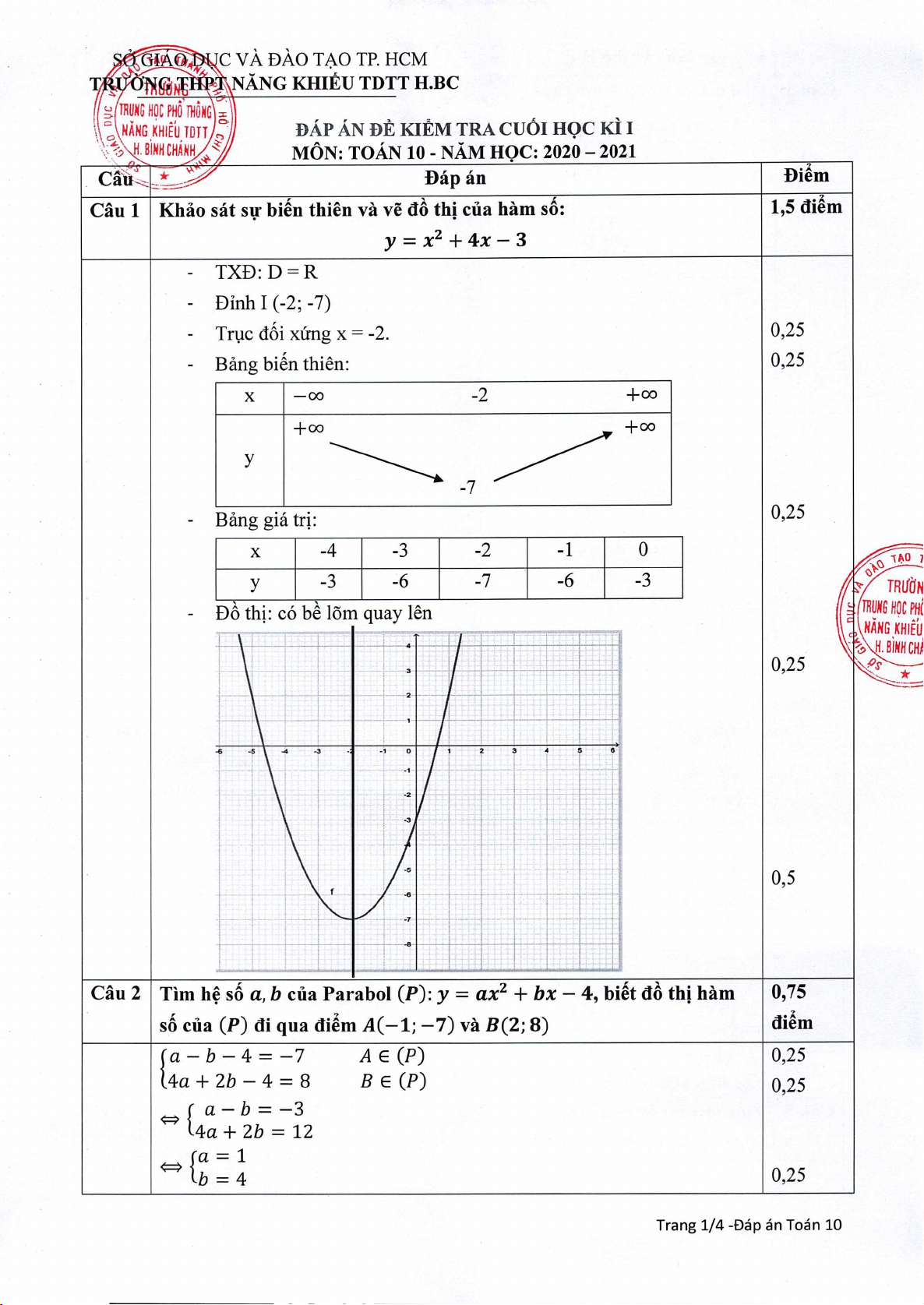
Khão sat sr bin thiên và ye d thi cüa ham s&
yx
2
+4x-3
1,5 diem
-
TXD:D=R
-
Dinh I (-2; -7)
-
Tric dôi xlrng x = -2.
-
Bang bién thiên:
0,25
0,25
0,25
0,25
0,5
/
x
-x
-2
+00
y
+00
+00
-
Bânggiãtrj:
x
-4
-3
-2
-1
0
y
-3
-6
-7
-6
-3
-
Do thj: cO be tOrn
quay len
-€
.5
-
-3
-
-i
0
I
2
3
4
5
0
f
-e
-8
Câu 2
Tim he s6
a, b
cüa Parabol
(P):
y
ax
2
+
bx
—
4, bit do thj ham
s cüa
(P)
di qua dim
A(-1;
—7) và
B(2;
8)
0,75
diem
fa—b-4=-7
AE(P)
(4a + 2b — 4 = 8
B
e
(P)
f
a — b = —3
(-4a + 2b = 12
lb=4
0,25
0,25
0,25
Trang 1/4 -Dáp an Toán 10
Vy Parabol cn tim là
(P): y
=
x
2
+ 4x
-
4
Câu 3
Giãi các phtro'ng trInh sau:
1,5 diem
a)I7x+61=I3x
-
21
b)V3x
2
_9x+1=x_2
a)
I
7
x+61=I3x
-
21
[7x
+ 6
=
3x
-
2
[7x+6=-3x+2
0,25
[4x
=
—8
10x
=
—4
0,25
x=-2
2
0,25
Vy S
=
{_2;
_.)
b)
V3x2_9x+1=x_2
(x —2 ~ 0
t3x
-
9x
+
1
=
(x
-
2)
2
0,25
(
x>2
t2x2
-
5x— 3
=
0
(
x~2
0,25
x=3
0,25
x
=
--
(1)
VyS
=f3}
Câu4
3x=6
0,75
Giãi h
phtro'ng trinh sau:
2x + y
=
5
diem
x+y+z=6
3x=6
2x+y= 5
x+y+z=6
x=2
0,25
2+y+z=6
x=2
0,25
2+y+z=6
x=2
y=
1
z=3
0,25
Vy h cO nghirn (x; y;
z)
=
(2; 1; 3)
Câu 5
TIm m d phtro'ng trInh x
2
+ (2m + 1)x +
m
2
-
3m
-
4
=
0 có 2
1,0 diem
nghim x
1
; x
2
thöa mAn x + x
=
37.
+) Pt có 2 nghim
(2m +
1)2
-
4(m
2
-
3m
-
4) ~ 0
Trarig2/4-DapánToán 10
4='4m
2
+4m+1-4m
2
+12m+16~0
+)x +x
=
37= (x
1
+x
2
)
2
—2x
1
x
2
=
37.
(x
1
+ x
2
=
—(2m
Theo dinh
ii
Vi
-
et ta co:
-
2
-
x
1
x
2
—m
3m
(1)
[—(2m + 1)1
2
-
2(m
2
-
4=4m
2
+4m+1-2m
2
+6m+837
=2m
2
+10m-28=0=I
Vy giá trj cn tIm là
m
=
2.
17
37
0,25
0,25
025
0,25
(1)
+
1)
-
.
Do do:
3m
-
4)
=
lm=2
(N)
Lm
=
—7
(L)
Câu 6
Trong mt phng
a)
Xác
d!nh
tQa
b)
Xác
d!nh
toi
Oxy cho ba dim
A(-1;
3);
B(2;
1);
C(3;
5).
1,0 diem
d
cüa các vecto'
AB.
d tr9ng tam G cüa
LABC
a)
Xác djnh t9a d
cüa vectcY
AB.
=
(XB
XAYB
YA)
0,25
=
(2
-
(-1); 1
-
3)
=
(3; —2).
0,25
b)
Xác djnh to d tr9ng
tam
G cüa
LXABC
I
XA+XB+XC
—1+2+3
4
0,25
X
=
3
3
TO
I
Y
A
+Y
B
+Y
C
3+1+5
3
0,25
YG
=
VayG(±;3)
Câu
7
Trong mt phng Oxy cho
i
=
(1; —5),
=
(-2; —7).
2,5 dim
A
a)
Tinh tich vo hiro'ng a.
b
A
b)
Phan tich vecto'
c
=
(7; —1) theo 2 vecto a va
b.
c)
TIm
m
dé vecto'
=
(2m
2
+
5m
+
3; 2) vuông góc
vôi
vecto'
ii.
a)
TInh
tIch vô hming
a.
0,25
025
a.
b
=
x
1
. x
2
+ y
1
. y
2
=
1. (-2) + (-5). (7)
0,25
=33.
b)
Giã ü
=
a
+
yb
0,25
(
7=x-2y
(x=3
Taco:
=
—5x
-
'7y
(y
=
—2
0,25
0,25
Vayc= 3d-2b
c)
c/a=o
1.(2m
2
+8m-2)+(-5).m= 0
0,25
Trang 3/4 -Dáp an Toán 10
'=2m
2
+8m-2-5m=0
=2m
2
+3m-2=0
Vâyrn=
m=-2
1
m=
—2hocm
0,25
0,25
0,25
Câu 8
TIm
giá
trj nhó nht cüa ham s
1,0 dim
x
12
1
y
=
+
4x
—
1
,
v&ix>
L
i.
x
12
y
=-+--
3
4x-1
-
4x
-
1 + 1
12
-
4x
-
1
12
Taco
0.25
1
4x-1
x>=4x-1>04=
12
>0
1
12
x>-4=4x-1>0=
>0
4
4x-1
Ap
4x-1
12
hai
diing BDT Co-si cho
so
va
12
4x-1
4x-1
12
1
I4x-1
12
1
1
25
12
+41+~24
12
4x_1+122+1212
1)
2
12
2
(4x—
=
0.25
12
4x-1
16x
2
-
8x
-
143..
13
x=—(n)
0.25
Vy
x
=
--(1)
4
25
.
13
0.25
Miny
=
-
khi
x
=
-
12
4
Trang 4/4 -Dáp an Toán 10
Bấm Tải xuống để xem toàn bộ.
Preview text:
Document Outline
- Page 1
- Page 2
- Page 3
- Page 4
- Page 5