



Preview text:
SỞ GD & ĐT NGHỆ AN
ĐỀ THI KSCL HỌC SINH GIỎI LỚP 11
CỤM THI THPT YÊN THÀNH NĂM HỌC 2016 - 2017 Môn: Toán
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (6,0 điểm). x a) Giải phương trình: ( x + ) 4 2 sin 3 os c
− sin x(1+ cos x) − 3cos x −1 = 0. 2
b) Giải bất phương trình: 2 2 2 (x +1)( x + 2 + x + 2x + 3) >
x + 2 − 2x −1
Câu 2 (3,0 điểm).
Cho đa giác lồi (H) có 22 ca ̣nh. Go ̣i X là tâ ̣p hợp các tam giác có ba đı̉nh là ba đı̉nh
của (H). Cho ̣n ngẫu nhiên 2 tam giác trong X, tı́nh xác suất để cho ̣n được 1 tam giác có 1
ca ̣nh là ca ̣nh của đa giác (H) và 1 tam giác không có ca ̣nh nào là ca ̣nh của đa giác (H).
Câu 3 (2,0 điểm). Cho dãy số (u ) xác định bởi: n u = 2 9 1 . Tìm 3 lim
(n − n).u . 2
n(n −1)u = u + 2u + ...+ (n −1)u , n ∀ > 1,n ∈ . 2 n n 1 2 n 1 −
Câu 4 (5,0 điểm). Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Các điểm H, K lần lượt
là trung điểm của AD, C’D’. Điểm M thuộc đoạn BC’, N thuộc đoạn AB’. Đường thẳng
MN tạo với mặt phẳng (ABCD) một góc 0 45 .
a) Chứng minh rằng: AK ⊥ BH ;
b) Chứng minh rằng: MN ≥ (2− 2)a.
Câu 5 (2,0 điểm). Trong mặt phẳng Oxy, cho tam giác ABC; đường thẳng AD là phân
giác trong góc Â. Trên đoạn AD lấy hai điểm M, N ( M, N khác A và D ) sao cho
ABN CBM . Đường thẳng CN cắt đường tròn ngoại tiếp tam giác ABN tại điểm F; biết
phương trình FA là x + y −8 = 0 và M ( 3 − ; 1 − ), B( 4 − ; 2
− ) . Xác định tọa độ điểm A biết đường
tròn ngoại tiếp tam giác AMC đi qua điểm Q(0; 22) . Câu 6 (2,0 điểm).
Cho các số thực dương a,b,c thỏa mãn ab + bc + ca = 1. Chứng minh rằng : a b c 3 3 + + ≥ . 2 2 2 2 2 2 b + c + 2 c + a + 2 a + b + 2 8
……………. Hết …………….
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Họ và tên thí sinh…………………….…………………………… Số báo danh……………………………………
HƯỚNG DẪN CHẤM ĐỀ THI KSCL ĐỘI TUYỂN HSG CỤM THPT YÊN THÀNH
(Hướng dẫn chấm này gồm 04 trang) Câu Nội dung Điểm 1. a. 3,0 (6,0đ) x x x 4 2 2 Pt ⇔ 2(s inx + 3) os c − 2sin . x os c − 6cos + 2 = 0 0,5 2 2 2 x x 4 2 ⇔ (sinx + 3) os c − os c (s inx + 3) +1 = 0 0,5 2 2 x x 2 2 ⇔ os c (s inx + 3)( os c −1) +1 = 0 0,5 2 2 1 2 3 2
⇔ − (sinx + 3)sin x +1 = 0 ⇔ sin x + 3sin x − 4 = 0 0,5 4 sinx = 1 ⇔ 0,5 sinx = 2 − (vn) π
⇔ x = + k2π (k ∈) 0,5 2 b. 3,0 2 2 2 0,5
Đặt: a = x + 2 (a ≥ 2) b − a −1 ⇒ x = 2 2 b
= x + 2x + 3 (b ≥ 2) BPT trở thành: 1 1 2 2 2 2 2 2 b − a +
(b − a −1)a +
(b − a +1)b > 0 1,0 2 2 2
⇔ (b − a)(b + a +1) > 0 0,5 2 2
⇔ b > a hay x + 2x + 3 > x + 2 0,5 1
⇔ x > − . Vậy tập nghiệm của bpt là: 1 S = (− ; +∞) 0,5 2 2 2.
+) Đa giác lồi (H) có 22 ca ̣nh nên có 22 đı̉nh. 0.5
(3,0đ) +) Số tam giác có 3 đı̉nh là ba đı̉nh của đa giác (H) là 3 C = 1540. 22
+) Số phần tử của không gian mẫu Ω là 2 n(Ω) = C = 1185030 0,5 1540
Số tam giác có một ca ̣nh là ca ̣nh của đa (H) là 22.18 = 396 0,5
+) Số tam giác có hai ca ̣nh là ca ̣nh của đa (H) là 22
Số tam giác không có ca ̣nh nào là ca ̣nh của đa (H) là: 1540 - 396 - 22 = 1122 0,5
+) Go ̣i A là biến cố “ hai tam giác được cho ̣n có mô ̣t tam giác có 1 ca ̣nh là ca ̣nh của
(H) và 1 tam giác không có ca ̣nh nào là ca ̣nh của (H)"
Số phần tử của A là 1 1 n(A) = C .C 0,5 396 1122 1 1 n(A) C .C 748 0,5
Xác suất của biến cố A là 396 1122 p(A) = = = n(Ω) 1185030 1995 3. 1 0,5 (2,0đ) Ta có:u = 2 3 Với n ≥ 3, ta có: 3
u + 2u + ... + nu = n u (1) 1 2 n n 3
u + 2u + ... + (n −1)u
= (n −1) u (2) 1 2 n 1 − n 1 − Từ (1) và (2), suy ra: 3 3
nu = n u − (n −1) u 0,5 n n n 1 − 2 3 (n −1) n −1 n ⇒ u = u = . u n 3 n 1 − n 1 − n − n n n +1 2 2 2
n −1 n − 2 2 n n −1 3 0,5 ⇒ u = . ... . . ... u n 2
n n −1 3 n +1 n 4 4 ⇒ 0,5 u = n 2 n (n +1) Do đó: 9 1 3 lim
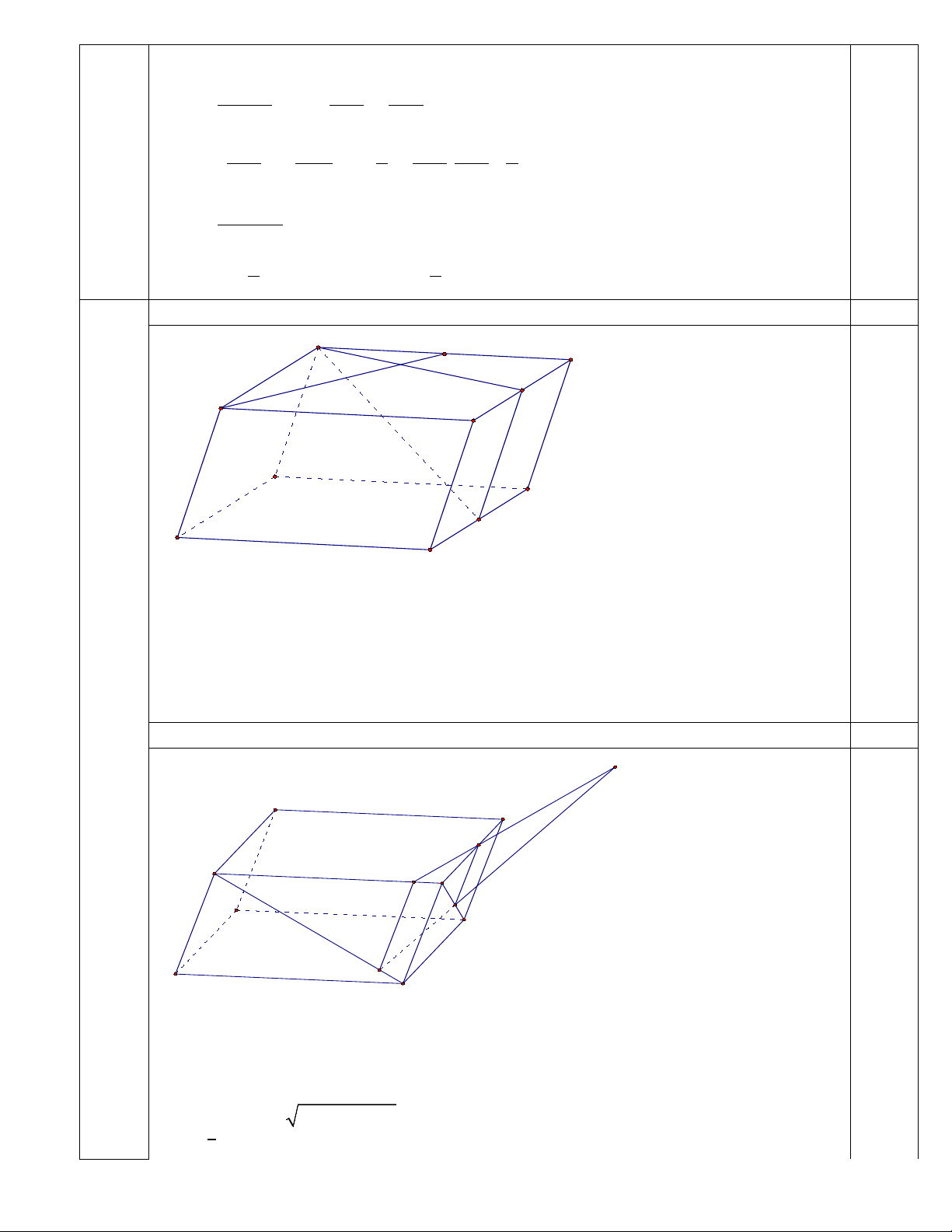
(n − n).u = lim18(1− ) = 18 . 2 n n 4. a. 3,0 (5,0đ) A 1,0 H D E B C A' D' K B' C'
Gọi E là trung điểm của cạnh CD, ta có: KE ⊥ (ABCD) ⇒ KE ⊥ BH (1)
Mặt khác, ta có: ABH = DAE ( .
c g.c) ⇒ ABH DAE 0,5 ⇒ 0 AHB HAE AHB ABH 90 0,5
⇒ BH ⊥ AE (2) 0,5
Tứ (1) và (2), suy ra: BH ⊥ (AEK) ⇒ BH ⊥ AK 0,5 b. 2,0 P 0,5 D C M' A N' B M D' C' A' N B'
Gọi M’, N’ lần lượt là hình chiếu của M, N trên (ABCD). Không mất tính tổng quát
giả sử MM’< NN’. Gọi P = MN ∩ M ' N ', khi đó: 0
(MN,(ABCD)) MPM ' 45 , MM ' = BM ', NN ' = AN ' = a − BN ', MN = PN − PM 0 0 0 ⇒ MN os c 45 = PN os c 45 − PM os c
45 = PN '− PM ' = M ' N ' (1) 0,5 Do đó: 2 2 0 M ' N ' =
BN ' + BM ' = MN os c 45 Ta có: 0 0 0
MN sin 45 = PN sin 45 − PM os c
45 = NN '− MM ' = a − (BN '+ BM ') (2) Từ (1) và (2) suy ra: 0,5 0 0 2 2 MN ( 2 os c 45 + sin 45 ) =
2(BN ' + BM ' ) + a − (BN '+ BM ')
≥ (BN '+ BM ') + a − (BN '+ BM ') = a 0,5 (BĐT Bunhiacôpxki)
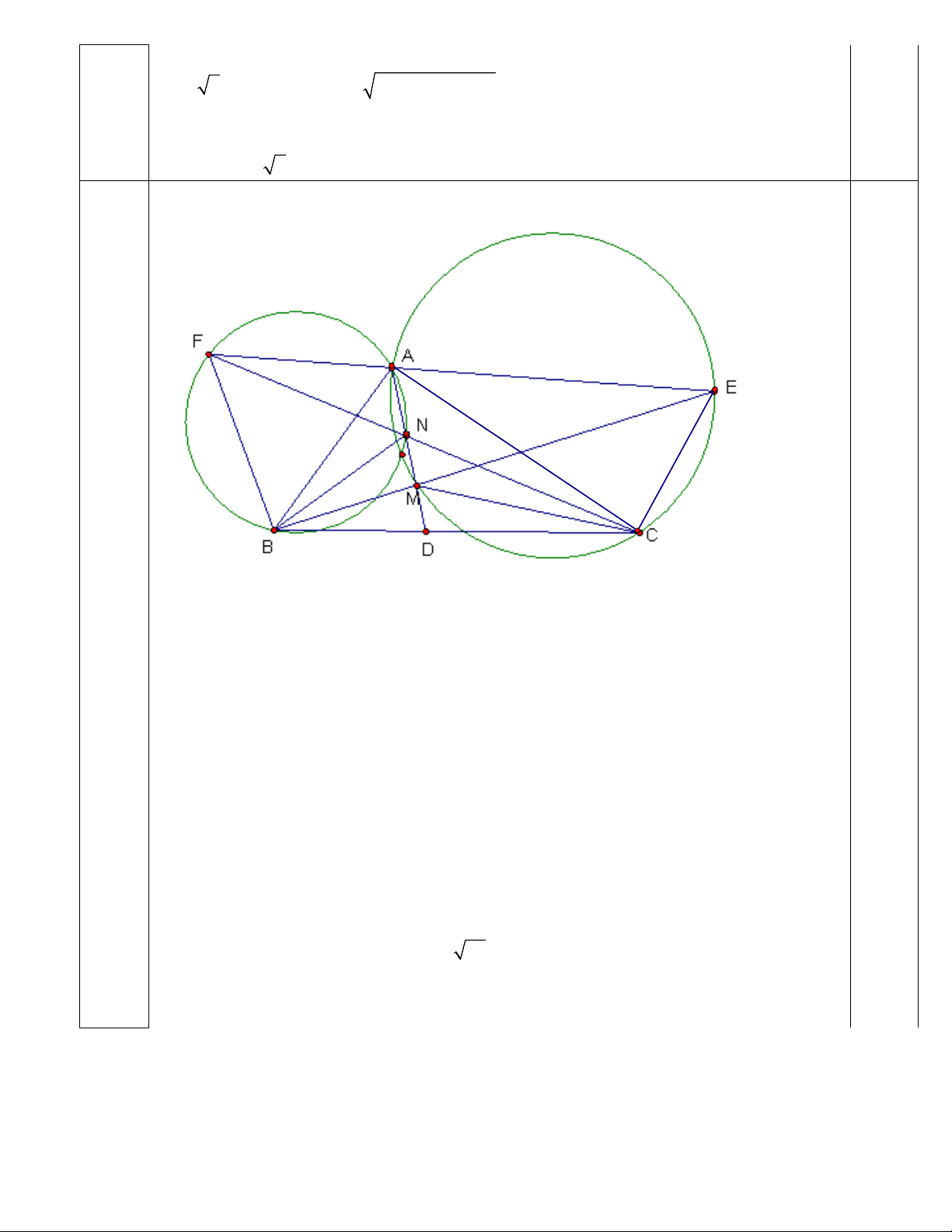
⇒ MN ≥ (2 − 2)a 5. (2,0đ) 0,5
Gọi E là giao điểm thứ hai của BM và đường tròn ngoại tiếp tam giác AMC. Ta chứng minh E thuộc AF.
Thật vậy tứ giác AFBN nội tiếp nên
NAB NFB Tương tự MAC MEC
, theo giả thiết
NAB MAC , suy ra: NFB MEC
Do đó tứ giác BCEF nội tiếp. Suy ra
CFE CBE NBA
NFA NFE . Suy ra A, E, F thẳng hàng.
Đường thẳng BM đi qua B và M nên có phương trình: x − y + 2 = 0 .
E = AF ∩ BM , suy ra tọa độ của E là nghiệm của hpt:
x + y − 8 = 0 x = 3 ⇔ ⇒ 0,5 E(3;5)
x − y + 2 = 0 y = 5
Đường tròn (T) ngoại tiếp tam giác AMC có phương trình dạng: 2 2 2 2
x + y − 2ax − 2by + c = 0 (a + b − c > 0)
6a + 2b + c = 10 − a = 2 0,5
Vì M, Q, E thuộc (T) nên ta có hpt: 2 − 22b + c = 22 − ⇔ b = 0 (tm)
6a +10b − c = 34 c = 22 − Suy ra (T) có pt: 2 2
x + y − 4x − 22 = 0 .
A là giao điểm của AE và (T) nên tọa độ điểm A là nghiệm của hpt: x = 7 0,5
x + y − 8 = 0 y = 1 ⇔ ⇒ ( A 7;1) 2 2 x y 4x 22 0 + − − = x = 3 y = 5 Vậy ( A 7;1)
Có ab + bc + ca = 1 nên 6. 2 2 2 2 2 2 2 2 2 2
b + c + 2 = a + b + c + 2(ab + bc + ca) − a = (a + b + c) − a = S − a
(2,0đ) trong đó S = a +b + c và 2 2
S = (a + b + c) ≥ 3(ab + bc + ca) ≥ 3 ⇒ S ≥ 3 . 0,5 Khi đó a b c 3 3 + + ≥ 2 2 2 2 2 2 b + c + 2 c + a + 2 a + b + 2 8 a b c 3 3 2 2 2 ⇔ + + ≥ aS bS cS 3 3 2 ⇔ + + ≥ S 2 2 2 2 2 2 S − a S − b S − c 8 2 2 2 2 2 2 S − a S − b S − c 8 3 3 3 a b c 3 3 0,5 2 ⇔ + a + + b + + c ≥ S 2 2 2 2 2 2 S − a S − b S − c 8 3 3 3 a b c 3 3 2 ⇔ + + + S ≥ S 2 2 2 2 2 2 S − a S − b S − c 8 4 4 4 a b c 3 3 2 ⇔ + + + S ≥ S 2 3 2 3 2 3 aS − a bS − b cS − c 8
Lại có theo Cauchy-Schazw thì 4 4 4 2 2 2 2 a b c
(a + b + c ) + + ≥ 2 3 2 3 2 3 2 3 3 3 aS − a bS − b cS − c
S (a + b + c) − (a + b + c ) 0,5 2 2 2 2 2 2 2 2
S (a + b + c ) S (S − 2) S (S − 2) = ≥ = 4 3 3 3 4 2 2 2
S − (a + b + c)(a + b + c ) S − (S − 2) 4S − 4 (Vì 2 2 2 2 3 3 3 2 3 3 3
(a + b + c ) = ( a. a + b. b + c. c ) ≤ (a + b + c)(a + b + c ) ) 2 2 2 2
Ta đi chứng minh S(S − 2) 3 3 (S − 2) 3 3 2 + S ≥ S ⇔ +1 ≥ S 2 2 4(S −1) 8 4(S −1) 8 3 2 2 ⇔
2S − 3 3S + 3 3 ≥ 0 ⇔ (S − 3)(2S − 3S − 3) ≥ 0 0,5 2
⇔ (S − 3) (2S + 3) ≥ 0 (luôn đúng S ∀ ≥ 3)
Vậy BĐT (*) được chứng minh, dấu "=" xảy ra khi và chỉ khi 1
a = b = c = . 3
…………………….Hết…………………….
Ghi chú: HS giải cách khác đúng vẫn cho điểm tối đa.




