Đề thi KSCL Toán 10 THPTQG lần 3 năm 2018 – 2019 trường Triệu Sơn 2 – Thanh Hoá

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh lớp 10 đề thi khảo sát chất lượng môn Toán 10 theo định hướng thi THPT Quốc gia lần 3 năm học 2018 – 2019 trường THPT Triệu Sơn 2 – Thanh Hoá, đề thi gồm 04 trang với 50 câu trắc nghiệm

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

11 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 01 - Mã đề 132 - https://toanmath.com/
TRƯỜNG THPT TRIỆU SƠN 2
(ĐỀ CHÍNH THỨC)
(Đề thi gồm 50 câu 4 trang)
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG
THEO ĐỊNH HƯỚNG THI THPT QUỐC GIA – LẦN 3
NĂM HỌC 2018 - 2019
MÔN: TOÁN. LỚP 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Mã đề: 132
Họ và tên.............................................SBD......................Phòng thi ……………………
Câu 1: Cho hình vuông
ABCD
cạnh
a
. Trên các cạnh
,
AB
,
BC
,
CD
lần lượt lấy các điểm
,
M
,
N
,
P
Q
sao cho
(0 )
AM BN CP DQ x x a
. Nếu
2
.
2
a
PM DC
thì giá trị của
x
bằng:
A.
a
. B.
2
a
. C.
3
4
a
. D.
4
a
.
Câu 2: Cho
2
: 4 3
P y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên
;2
. B. Hàm số nghịch biến trên
;2
.
C. Hàm số nghịch biến trên
;4
. D. Hàm số đồng biến trên
;4
.
Câu 3: Tập nghiệm của bất phương trình
5
11
x
x
là.
A.
5;0S . B.
5;0\RS .
C.
 ;50;S . D. RS
.
Câu 4: Cho hai đường thẳng
: 2 3 0
d x y
và
: 3 2 0
x y
. Phương trình đường thẳng
'
d
đối
xứng với
d
qua
là:
A.
13 11 2 0
x y
. B.
11 2 13 0
x y
. C.
11 13 2 0
x y
. D.
11 2 13 0
x y
.
Câu 5: Tập nghiệm của bất phương trình
2 2 5 3
x x x
là:
A.
;2 6;
 
. B.
;1

.
C.
;2 4 5;

. D.
100;2
.
Câu 6: Nếu
;
x y
là nghiệm của hệ phương trình:
2 2
4 1
4 2
x xy y
y xy
. Thì
xy
bằng bao nhiêu ?
A.
4.
B.
1.
C. Không tồn tại giá trị của
xy
. D.
4.
Câu 7: Tam giác
ABC
có
4
AB
,
6
AC
và trung tuyến
3
BM
. Tính độ dài cạnh
.
A.
2 5
. B.
17
. C.
4
. D.
8
.
Câu 8: Đồ thị sau đây là của hàm số nào?
A.
2
4
y x x
. B.
2
4 3
y x x
. C.
2
4 3
y x x
. D.
2
4 3
y x x
.
Câu 9: Trong mặt phẳng
Oxy
cho
3
điểm
1;3 2;0, ,
6;2
B CA . Tìm tọa độ
D
sao cho tứ
giác A
BCD
là hình bình hành.
A.
9; 1
. B.
3;5
. C.
5;3
. D.
1;9
.
Câu 10: Cho tập hợp
2
4 0
B x x
. Tập hợp nào sau đây đúng
A.
2;4
B . B.
4;4
B . C.
2;2
B . D.
2;4
B .
Câu 11: Cho các số thực x, y, z thỏa mãn x + y + z = 0, x
2
+ y
2
+ z
2
= 8. Tìm giá trị nhỏ nhất của biểu
thức
P x y z
A. 3 B.
5
4
C. 5 D. 4
Câu 12: Tập xác định
D
của hàm số
1
3 2 1
x
y
x x
là:
A.
1
D ; \ 3
2

. B.
1
D ; \ 3
2

. C.
1
D ; \ 3
2

. D.
D
.
Câu 13: Để đo chiều cao một cây ở góc sân trường người ta thực hiện đặt giác kế ở hai vị trí A và B như
hình vẽ để ngắm. Biết khoảng cách
)(3 métAB
, độ cao ngắm của giác kế so với mặt đất là
)(2,1 métCH
và các góc ngắm
00
37,55
.
Chiều cao của cây (làm tròn đến mét) là.
A. 4 mét. B. 6 mét. C. 5 mét. D. 7 mét.
Câu 14: Cho
1
sin
3
. Tính giá trị biểu thức
2 2
3sin cos
P
.
A.
9
25
P . B.
11
9
P
. C.
9
11
P
. D.
25
9
P .
Câu 15: Với giá trị thực nào của tham số m thì hàm số mxmy 2)1(
đồng biến trên R?
A.
1;m . B.
( ,2)
m

. C.
 ;1m . D.
(0,2)
m
.
Câu 16: Phương trình
2
1 2 2 0
m x mx m
vô nghiệm khi:
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
.
Câu 17: Cho đường tròn (C) :
2 2
4 6 5 0
x y x y
. Đường thẳng
d
đi qua
(3; 2)
A
và cắt
( )
C
theo
một dây cung ngắn nhất có phương trình là
A.
1 0
x y
. B.
1 0
x y
. C.
1 0
x y
. D.
2 2 0
x y
.
Câu 18: Cho ba tập
2;0
A
;
: 1 0
B x x
;
: 2
C x x
. Khi đó
A.
\ 2; 1
A C B
. B.
\ 2; 1
A C B
.
C.
\ 2; 1
A C B
. D.
\ 2; 1
A C B
.
Câu 19: Phương trình
2 4 2 4 0
x x
có bao nhiêu nghiệm?
A. Vô số. B. 2. C. 0. D. 1.
Câu 20: Số nghiệm của hệ phương trình
3 6 5
2 4 3
x y
x y
là
A.
0
. B.
1
. C.
2
. D. vô số.
Trang 02 - Mã đề 132 - https://toanmath.com/
Câu 21: Khoảng cách từ điểm
1
(
1;
)
M
đến đường thẳng
: 3 4 17 0
x y
bằng:
A.
2
5
. B.
18
5
. C.
10
5
. D.
2
.
Câu 22: Với các điểm O, A, B và C bất kì. Chọn khẳng định luôn đúng trong các khẳng định sau.
A.
OAOBAB
. B.
BCACAB
. C.
BAOBOA
. D.
COCAOA
.
Câu 23: Có bao nhiêu giá trị của a để phương trình
2 2
2 3 2 5 8
x x a x x
có nghiệm duy nhất.
A. vô số B. 3 C. 1 D. 0
Câu 24: Giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
2
4 3
y f x x x
trên đoạn
2;1
là
A.
0; 15.
M m
B.
15; 1.
M m
C.
15; 0.
M m
D.
1; 2.
M m
Câu 25: Hệ phương trình
2 2
5
x y
x y
có bao nhiêu nghiệm?
A.
3.
B.
2.
C.
4.
D.
1.
Câu 26: Cho tam giác đều ABC có độ dài cạnh bằng 3. Đặt
u AB AC
. Độ dài vectơ
u
bằng:
A. 3. B. 3 . C. 32 . D. 33 .
Câu 27: Tổng các nghiệm của phương trình
2
5 4 4
x x x
bằng:
A.
6.
B.
12.
C.
12.
D.
6.
Câu 28: Phương trình
2 ( 1) 0
x x m
có ba nghiệm phân biệt, giá trị thích hợp của tham số m là
A.
9
0.
4
m
B.
2 1.
m
C.
9
0 .
4
m
D.
1 2.
m
Câu 29: Tập ngiệm của bất phương trình:
2
5 2( 2)
x x x
là:
A.
– ;1
)
) ;( (4
. B.
1;4
. C.
(1;4)
. D.
– ;1
)
;( ] [4
.
Câu 30: Tập nghiệm của bất phương trình
235 x là.
A.
1;S . B.
5
3
;S . C.
1;
5
1
S . D.
5
1
;S .
Câu 31: Phương trình sau có bao nhiêu nghiệm:
4 3 0
x x
A. 0 B. 3 C. 1 D. 2
Câu 32: Hỏi tập hợp nào là tập hợp rỗng trong các tập hợp sau?
A.
2
4 2 0
x Q x x
. B.
2
4 3 0
x R x x
.
C.
1
x Z x
D.
2
6 7 1 0
x Z x x
.
Câu 33: Cho đường thẳng
: 3 – 4 –12 0.
d x y
Phương trình các đường thẳng qua
2; –1
M và tạo với
d
một góc
4
là
A.
7 – 15 0; 7 – 5 0
x y x y
. B.
7 15 0; – 7 – 5 0
x y x y
.
C.
7 – –15 0; 7 5 0
x y x y
. D.
7 –15 0; – 7 5 0
x y x y
.
Câu 34: Xác định vị trí tương đối của hai đường thẳng
1
2 5
:
3 6
x t
y t
và
2
7 5
:
3 6
x t
y t
.
A. Trùng nhau. B. Song song nhau.
C. Vuông góc nhau. D. Cắt nhau nhưng không vuông góc.
Câu 35: Phương trình tổng quát của đường thẳng đi qua
( )
2; 1 , 2;5
A B là:
A.
2 0.
x
B.
2 0.
x
C.
1 0.
x y
D.
2 7 9 0.
x y
Câu 36: Mệnh đề nào sau đây sai?
Trang 03 - Mã đề 132 - https://toanmath.com/
A.
a b
c d
a c b d
. B.
a b
c d
ac bd
.
C.
a b
c d
a c b d
. D.
ac bc
a b
.
0
c
Câu 37: Hệ bất phương trình
2
2
16 0
2 2 7 5 0
x
x x x
có số nghiệm nguyên là
A. 4. B. 2. C. Vô số. D. 3.
Câu 38: Phương trình tổng quát của đường thẳng đi qua M(2;-1) và có vectơ chỉ phương
3; 7
u
là:
A. −3x + 7y + 13 = 0. B. 7x + 3y +13 = 0. C. 3x + 7y + 1 = 0. D. 7x + 3y −11 = 0.
Câu 39: Gọi
1 2
,
x x
là hai nghiệm của phương trình
2 2
2 2 2 0
x mx m
(
m
là tham số). Tìm giá trị
lớn nhất
max
P
của biểu thức
1 2 1 2
2 4 .
P x x x x
A.
max
23
.
4
P B.
max
25
.
4
P C.
max
9
.
4
P
D.
max
8.
P
Câu 40: Cho hàm số có bảng biến thiên như sau:
x
3 7
y
2
-1
Hàm số đồng biến trên khoảng nào sau đây?
A.
;7

. B.
;2

và
1;
. C.
7;3 . D.
3; và
;7 .
Câu 41: Xác định dạng của tam giác ABC biết :
c a b
r r r r
. (
r
là độ dài bán kính đường tròn nội tiếp
tam giác ABC;
, ,
a b c
r r r
tương ứng là độ dài bán kính các đường tròn bàng tiếp các góc A, B, C)
A. Tam giác cân đỉnh B B. Tam giác vuông cân đỉnh B
C. Tam giác vuông đỉnh A D. Tam giác vuông đỉnh C
Câu 42: Cung tròn có số đo là
5
4
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.
A.
15
. B.
172
. C.
225
. D.
5
.
Câu 43: Cho
ABC
có
2; 1
A
,
4;5
B ,
3;2
C . Viết phương trình tổng quát của đường cao
CH
.
A.
2 6 5 0
x y
. B.
3 3 0
x y
. C.
3 11 0
x y
. D.
1 0
x y
.
Câu 44: Đường tròn
2 2
6 8 0
x y x y
có bán kính bằng
A. 5. B. 25. C.
10
. D. 10.
Câu 45: Cho
2
sinx cos
3
x
.Khi đó giá trị của biểu thức P =
sinx cos
x
là
A.
14
3
. B.
2
3
. C.
14
9
. D.
3
2
.
Câu 46: Cho tam giác có ba cạnh lần lượt là
5
,
12
,
13
. Khi đó diện tích tam giác bằng :
A.
60
. B.
30
. C.
34
. D.
7 5
.
Câu 47: Tọa độ đỉnh
I
của parabol
2
: 4
P y x x
là:
A.
1;3
I . B.
2;4
I . C.
1; 5
I
. D.
2; 12
I .
Câu 48: Tập hợp các giá trị thực của m để bất phương trình 02)2(2)2(
22
xmxm nghiệm đúng
với Rx
là.
A.
 ;04; . B.
0;4 . C.
0; )

. D.
0;4 .
Câu 49: Có bao nhiêu giá trị m nguyên để bất phương trình
2
( 1) 2( 1) 3 0
m x m x
vô nghiệm.
Trang 04 - Mã đề 132 - https://toanmath.com/
A. 2. B. 1. C. 4. D. 3.
Câu 50: Phương trình
2 3
2 2 5 1
x x
có bao nhiêu nghiệm.
A. 0 B. 3 C. 1 D. 2---------------------------
-------------------- HẾT ----------
Trang 05 - Mã đề 132 - https://toanmath.com/
HƯỚNG DẪN MỘT SỐ CÂU KHÓ
Câu 1. Để đo chiều cao một cây ở góc sân trường người ta thực hiện đặt giác kế ở hai vị trí A và B như
hình vẽ để ngắm. Biết khoảng cách )(3 métAB
, độ cao ngắm của giác kế so với mặt đất là
)(2,1 métCH
và các góc ngắm
00
37,55
.
Chiều cao của cây (làm tròn đến mét) là.
A. 4 mét. B. 5 mét. C. 6 mét. D. 7 mét.
Lời giải
Chọn C
55 37 18
o o o
A DB
Theo định lý Sin cho tam giác ABD ta có
37
. 37 3. 37
18
5,843( ).
o
o o
o
AB AD
SinD Sin
AB Sin Sin
AD
SinD Sin
m
Đường thẳng đi qua B, A
, H vuông góc với HD
Nên AHD vuông tại H và HD = AD.Sin 55
o
28,451.Sin 49
o
4,786 (m).
Chiều cao của cây là: CD
HD+HC
4,786 +1,2
5,986
6(m).
Câu 2. Xác định dạng của tam giác ABC biết rằng
c a b
r r r r
(
r
là độ dài bán kính đường tròn nội tiếp tam giác ABC;
, ,
a b c
r r r
tương ứng là độ dài bán kính các đường
tròn bàng tiếp các góc A, B, C)
A. Tam giác cân đỉnh B B. Tam giác vuông đỉnh C
C. Tam giác vuông đỉnh A D. Tam giác vuông cân đỉnh B
Lời giải
D
H
A B
B
1
A
1
C
3m
1,2m
55
o
37
o
132 1
C
132 2
B
132 3
A
132 4
D
132 5
C
132 6
C
132 7
A
132 8
B
132 9
B
132 10
C
132 11
D
132 12
A
132 13
B
132 14
B
132 15
A
132 16
A
132 17
C
132 18
A
132 19
A
132 20
A
132 21
D
132 22
D
132 23
C
132 24
C
132 25
B
132 26
D
132 27
D
132 28
A
132 29
D
132 30
C
132 31
C
132 32
A
132 33
C
132 34
D
132 35
A
132 36
B
132 37
B
132 38
D
132 39
B
132 40
D
132 41
D
132 42
C
132 43
B
132 44
A
132 45
A
132 46
B
132 47
B
132 48
A
132 49
C
132 50
D
Trang 06 - Mã đề 132 - https://toanmath.com/
Chọn B
Ta có
( ) ( ) ( )
a b c
S pr p a r p b r p c r
1 1 1 1
c a b
S S S S
r r r r
p c p p a p b p c p p a p b
( ) ( )( ) p(a b c) ab
p p c p a p b
2 2
( )(a b c) 2 ( ) 2
a b c ab a b c ab
2 2 2
a b c
Vậy tam giác ABC là tam giác vuông đỉnh C
Câu 3. Tập nghiệm của bất phương trình
2 2 5 3
x x x
là:
A.
;2 4 5;

. B.
;1

.
C.
;2 6;
 
. D.
100;2
.
Lời giải
Chọn A
Ta có:
2
2
3 0
3
2 2 5 0
;2 5;
2 2 5 3
3 0
3
2 2 5 6 9
8 11 0
x
x
x x
x
x x x
x
x
x x x x
x x
3
;2 5;
;2
3
4 5;
;4 5 4 5;
x
x
x
x
x
x
 



Vậy tập nghiệm của bất phương trình là:
;2 4 5;S
 
.
Câu 4. Cho đường tròn
2 2
( ) : x 4 6 5 0
C y x y
. Đường thẳng
d
đi qua
(3; 2)
A
và cắt
( )
C
theo
một dây cung ngắn nhất có phương trình là
A.
1 0
x y
. B.
1 0
x y
. C.
2 2 0
x y
. D.
1 0
x y
.
Lời giải
Chọn A
H
I
M
N
A
.
2 2
; 4 6 5.
(3;2) 9 4 12 12 5 6 0.
f x y x y x y
f
Vậy
3; 2
A ở trong
C
. Đường tròn (C) có tâm I(2; 3).
Trang 07 - Mã đề 132 - https://toanmath.com/
Dây cung
MN
ngắn nhất
IH
lớn nhất
H A
MN
có vectơ pháp tuyến là
1; 1
IA
. Vậy
d
có phương trình:
1( 3) 1( 2) 0 1 0
x y x y
.
Câu 5. Cho hình vuông
ABCD
cạnh
a
. Trên các cạnh
,
AB
,
BC
,
CD
lần lượt lấy các điểm
,
M
,
N
,
P
Q
sao cho
(0 )
AM BN CP DQ x x a
. Nếu
2
.
2
a
PM DC

thì giá trị của
x
bằng:
A.
3
4
a
. B.
a
. C.
4
a
. D.
2
a
.
Lời giải
Chọn A
Ta có:
2
.
2
a
PM DC
2
.
2
a
PQ PN DC

2
. .
2
a
PQ DC PN DC

2
. .
2
a
PD DC PC DC
2
( )
2
a
a x a xa
2
2
2
2
a
ax a
3
4
x a
.
Câu 6. Phương trình
2 ( 1) 0
x x m
có ba nghiệm phân biệt, giá trị thích hợp của tham số m là
A.
9
0.
4
m
B.
2 1.
m
C.
9
0 .
4
m
D.
1 2.
m
Lời giải
Chọn A
2 ( 1) 0
x x m
2 ( 1)
x x m
Xét hàm số
2 1
y x x
2
2
2 , 2
2 , 2
x x x
x x x
Suy ra bảng biến thiên của hàm số
2 1
y f x x x
như sau:
Yêu cầu bài toán
9 9
0 0.
4 4
m m
Câu 7. Phương trình
2 3
2 2 5 1
x x
có bao nhiêu ngiệm.
A. 0 B. 3 C. 1 D. 2
Lời giải
Chọn D
ĐK:
1
x
Đặt
1
u x
;
2
1
v x x
( ; 0)
u v
.
PT trở thành:
2 2
2
2( ) 5
2
u v
u v uv
v u
+ Với
2
2 1 2 1
u v x x x
(vô nghiệm)
+ Với
2
2 1 2 1
v u x x x
2
5 37
5 3 0
2
x x x
(tmđk).
2
2
x x
2
2
x x
1
2
+∞
2
∞
f
(x)
x
9
4
0


Trang 08 - Mã đề 132 - https://toanmath.com/
Câu 8. Cho các số thực x, y, z thỏa mãn x + y + z = 0, x
2
+ y
2
+ z
2
= 8. Tìm giá trị nhỏ nhất của biểu thức
P x y z
A. 4 B. 5 C. 3 D.
5
4
Lời giải
Chọn A
2
2 2 2 2
2 2 2 2
2
P x y z x y z x y y z z x
P x y z x y z y z x z x y
Áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối ta có
2
y z y z x x x y z x
Chứng minh tương tự
2 2
,
y z x y z x y z
Vì vậy
2 2 2 2
2
P x y z
Thay
2 2 2 2
8 16 4
x y z P P
Dấu bằng có thể xảy ra, khi
, , 2; 2;0
x y z hoặc các hoán vị, ta có P = 4
Vậy min P = 4
Câu 9. Cho đường thẳng
: 3 – 4 –12 0.
d x y
Phương trình các đường thẳng qua
2; –1
M và tạo với
d
một góc
4
là
A.
7 – 15 0; 7 – 5 0
x y x y
. B.
7 15 0; – 7 – 5 0
x y x y
.
C.
7 – –15 0; 7 5 0
x y x y
. D.
7 –15 0; – 7 5 0
x y x y
.
Lời giải
Chọn C
Gọi
;
n A B
và
2 2
0
A B
là véctơ pháp tuyến của
Ta có:
2 2
2 2 2 2
3 4
cos 2 3 4 5
4
3 4 .
A B
A B A B
A B
2 2
7
7 48 7 0
7
B A
A AB B
A B
Với
7
B A
chọn
1, 7 7 5 0
A B x y
Với
7
A B
chọn
7, 1 7 15 0
A B x y
.
Câu 10. Có bao nhiêu giá trị của a để phương trình
2 2
2 3 2 5 8
x x a x x
có nghiệm duy nhất.
A. 0 B. 3 C. vô số D. 1
Lời giải
Chọn D
Phương trình tương đương với
2 2
2 3 2 8 5
x x x x a
Xét hàm số
2
2 2
2
1
3 5 2, , 2 ,
3
( ) 2 3 2 8
1
11 2, 2,
3
x x x
y f x x x x x
x x x

Suy ra, bảng biến thiên của hàm
2 2
2 3 2 8
y f x x x x x
như sau:
Trang 09 - Mã đề 132 - https://toanmath.com/
Yêu cầu bài toán
49 49
5
12 60
a a .
Câu 11. Cho hai đường thẳng
: 2 3 0
d x y
và
: 3 2 0
x y
. Phương trình đường thẳng
'
d
đối
xứng với
d
qua
là:
A.
13 11 2 0
x y
. B.
11 2 13 0
x y
.
C.
11 13 2 0
x y
. D.
11 2 13 0
x y
.
Lời giải
Chọn D
Giao điểm của
d
và
là nghiệm của hệ
2 3 0 2 3 1
1;1
3 2 0 3 2 1
x y x y x
A
x y x y y
.
Lấy
0;3
M d
. Tìm
'
M
đối xứng
M
qua
.
Viết phương trình đường thẳng
'
đi qua
M
và vuông góc với
:
': 3 3 0
x y
.
Gọi
H
là giao điểm của
'
và đường thẳng
. Tọa độ
H
là nghiệm của hệ
7
3 2 0 3 2
7 9
10
;
3 3 0 3 3 9
10 10
10
x
x y x y
H
x y x y
y
.
Ta có
H
là trung điểm của
'
MM
. Từ đó suy ra tọa độ
7 6
' ;
5 5
M
.
Viết phương trình đường thẳng
'
d
đi qua 2 điểm
A
và
'
M
: điểm đi qua
( 1;1)
A
, vectơ chỉ
phương
2 11
' ;
5 5
AM
vectơ pháp tuyến
11 2
;
5 5
n
.
11 2
': 1 1 0 11 2 13 0
5 5
d x y x y
.
Câu 12. Gọi
1 2
,
x x
là hai nghiệm của phương trình
2 2
2 2 2 0
x mx m
(
m
là tham số). Tìm giá trị
lớn nhất
max
P
của biểu thức
1 2 1 2
2 4 .
P x x x x
A.
max
8.
P
B.
max
25
.
4
P C.
max
9
.
4
P
D.
max
23
.
4
P
Lời giải.
Chọn B
Ta có
2 2 2
' 2 2 4
m m m
.
Phương trình có hai nghiệm khi và chỉ khi
2
' 4 0 2 2.
m m
*
Trang 10 - Mã đề 132 - https://toanmath.com/
Theo định lý Viet, ta có
1 2
2
1 2
.
2
2
x x m
m
x x
Khi đó
2
1 2 1 2
2 4 6 2 3 2 3
P x x x x m m m m m m
2
2
1 25 25
6
2 4 4
m m m
(do
2 2
m
).
Dấu
'' ''
xảy ra khi và chỉ khi
1
2
m
: thỏa
*
. Vậy
max
25
.
4
P
Câu 13. Nếu
;
x y
là nghiệm của hệ phương trình:
2 2
4 1
4 2
x xy y
y xy
. Thì
xy
bằng bao nhiêu ?
A.
4.
B.
1.
C. Không tồn tại giá trị của
xy
. D.
4.
Lời giải
Chọn C
Ta có :
2 2
4 1
x xy y
2
2
1 2
1 6
x y xy
x y xy
.
4 2 2 8 4
y xy y xy
8 4 0
x y x y xy
2 2
2 0
x y x y x y x y
2 2
1 1 3
0
2 2 2
x y x y
không có
giá trị của
x
,
y
thỏa nên không tồn tại
xy
.
Trang 11 - Mã đề 132 - https://toanmath.com/
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT TRIỆU SƠN 2
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG
THEO ĐỊNH HƯỚNG THI THPT QUỐC GIA – LẦN 3 (ĐỀ CHÍNH THỨC) NĂM HỌC 2018 - 2019 MÔN: TOÁN. LỚP 10
(Đề thi gồm 50 câu 4 trang)
Thời gian làm bài: 90 phút (Không kể thời gian giao đề) Mã đề: 132
Họ và tên. . . . . . . . . . . . . . . . . . . . . . .SBD. . . . . . . . . . . Phòng thi ……………………
Câu 1: Cho hình vuông ABCD cạnh a . Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm   2 a
M , N , P, Q sao cho AM BN CP DQ x (0  x a) . Nếu PM . DC  thì giá trị của 2 x bằng: a 3a a A. a . B. 2 . C. 4 . D. 4 .
Câu 2: Cho  P 2
: y x  4x  3 . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên   ;2 .
B. Hàm số nghịch biến trên   ;2 .
C. Hàm số nghịch biến trên  ;  4 .
D. Hàm số đồng biến trên  ;  4 . 1 1
Câu 3: Tập nghiệm của bất phương trình  là. x x  5 A. S   5 ; 0 .
B. S R \   5 ; 0 .
C. S    0 ;    ; 5 .
D. S R .
Câu 4: Cho hai đường thẳng d : 2x y  3  0 và  : x  3y  2  0 . Phương trình đường thẳng d ' đối
xứng với d qua  là:
A. 13x 11y  2  0 .
B. 11x  2 y 13  0 .
C. 11x  13 y  2  0 .
D. 11x  2 y  13  0 .
Câu 5: Tập nghiệm của bất phương trình 2 x  2 x  5  x  3 là: A.  ;  2 6; . B. ;  1 . C.  ;
 2  4  5; . D. 100;2 . 2 2
x  4xy y  1 Câu 6: Nếu  ;
x y  là nghiệm của hệ phương trình: 
. Thì xy bằng bao nhiêu ? y  4xy   2 A. 4  . B. 1.
C. Không tồn tại giá trị của xy . D. 4.
Câu 7: Tam giác ABC có AB  4 , AC  6 và trung tuyến BM  3 . Tính độ dài cạnh BC . A. 2 5 . B. 17 . C. 4 . D. 8 .
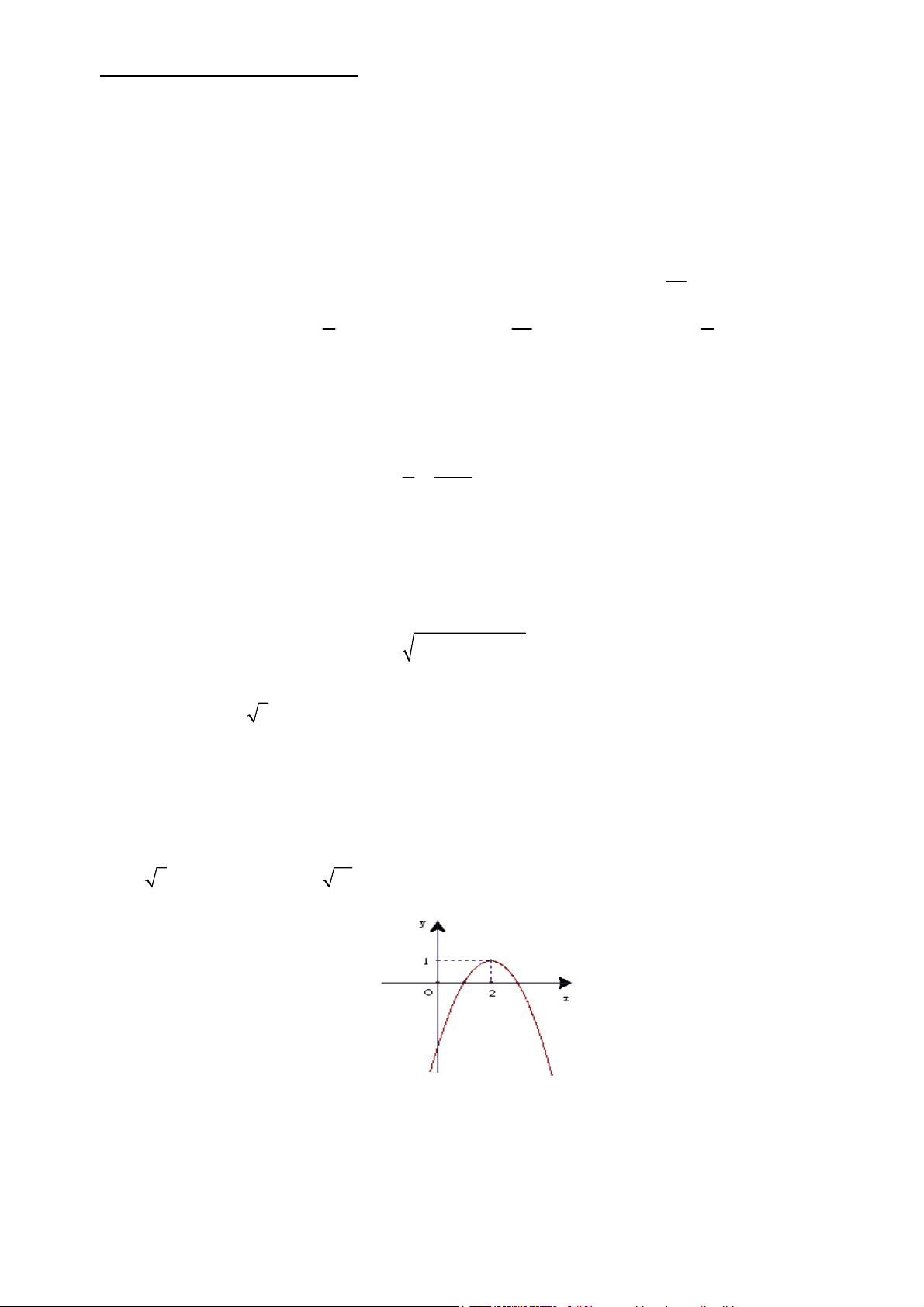
Câu 8: Đồ thị sau đây là của hàm số nào? A. 2
y  x  4x . B. 2
y  x  4x  3 . C. 2
y x  4x  3 . D. 2
y x  4x  3 .
Câu 9: Trong mặt phẳng Oxy cho 3 điểm A   1
 ;3, B  2;0,C  6;2 . Tìm tọa độ D sao cho tứ
giác ABCD là hình bình hành. A. 9;  1  . B. 3;5 . C. 5;3 . D.  1  ;9 .
Trang 01 - Mã đề 132 - https://toanmath.com/
Câu 10: Cho tập hợp B   2
x   x  4  
0 . Tập hợp nào sau đây đúng A. B   2  ;  4 . B. B   4  ;  4 . C. B   2  ;  2 .
D. B  2;  4 .
Câu 11: Cho các số thực x, y, z thỏa mãn x + y + z = 0, x2 + y2 + z2 = 8. Tìm giá trị nhỏ nhất của biểu
thức P x y z 5 A. 3 B. 4 C. 5 D. 4 x 1
Câu 12: Tập xác định D của hàm số y  là: x  3 2x 1  1   1  1  A. D   ;   \   3 .    .   B. D   ; \   3
C. D   ; \   3 . D. D   . 2   2  2    
Câu 13: Để đo chiều cao một cây ở góc sân trường người ta thực hiện đặt giác kế ở hai vị trí A và B như
hình vẽ để ngắm. Biết khoảng cách AB  (
3 mét) , độ cao ngắm của giác kế so với mặt đất là CH  ,
1 2(mét ) và các góc ngắm 0 0
 55 ,  37 .
Chiều cao của cây (làm tròn đến mét) là. A. 4 mét. B. 6 mét. C. 5 mét. D. 7 mét. Câu 14: Cho 1
sin . Tính giá trị biểu thức 2 2
P  3sin  cos . 3 9 11 9 25 A. P  . 25 B. P  . 9 C. P  . 11 D. P  . 9
Câu 15: Với giá trị thực nào của tham số m thì hàm số y  1
(  m)x  2m đồng biến trên R? A. m    1 ;  .
B. m  (, 2) . C. m    ;1 .
D. m  (0, 2) .
Câu 16: Phương trình m   2
1 x  2mx m  2  0 vô nghiệm khi: A. m  2 . B. m  2 . C. m  2. D. m  2  .
Câu 17: Cho đường tròn (C) : 2 2
x y  4x  6y  5  0 . Đường thẳng d đi qua A(3; 2) và cắt (C ) theo
một dây cung ngắn nhất có phương trình là
A. x y  1  0 .
B. x y 1  0 .
C. x y 1  0 .
D. 2x y  2  0 .
Câu 18: Cho ba tập A  2; 0 ; B  x   : 1  x  
0 ; C  x  : x   2 . Khi đó
A. A C  \ B  2;   1 .
B. A C  \ B  2;   1 .
C. A C  \ B  2;   1 .
D. A C  \ B  2;   1 .
Câu 19: Phương trình 2x  4  2x  4  0 có bao nhiêu nghiệm? A. Vô số. B. 2. C. 0. D. 1.  3x 6y 5
Câu 20: Số nghiệm của hệ phương trình    là
2x  4y    3 A. 0 . B. 1. C. 2 . D. vô số.
Trang 02 - Mã đề 132 - https://toanmath.com/
Câu 21: Khoảng cách từ điểm M (1; 1) đến đường thẳng  : 3x  4 y 17  0 bằng: 2 18 10 A. 5 . B. 5 . C. . D. 2 . 5
Câu 22: Với các điểm O, A, B và C bất kì. Chọn khẳng định luôn đúng trong các khẳng định sau.
A. AB OB OA .
B. AB AC BC .
C. OA OB BA .
D. OA CA CO .
Câu 23: Có bao nhiêu giá trị của a để phương trình 2 2
2x  3x  2  5a 8x x có nghiệm duy nhất. A. vô số B. 3 C. 1 D. 0
Câu 24: Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y f x 2
x  4x  3 trên đoạn  2   ;1 là
A. M  0; m  15.
B. M  15; m  1.
C. M  15; m  0.
D. M  1; m  2. x y  1
Câu 25: Hệ phương trình 
có bao nhiêu nghiệm? 2 2 x y   5 A. 3. B. 2. C. 4. D. 1.    
Câu 26: Cho tam giác đều ABC có độ dài cạnh bằng 3. Đặt u AB AC . Độ dài vectơ u bằng: A. 3. B. 3 . C. 2 3 . D. 3 3 .
Câu 27: Tổng các nghiệm của phương trình 2
x  5x  4  x  4 bằng: A. 6. B. 12. C. 1  2. D. 6  .
Câu 28: Phương trình x  2 (x 1)  m  0 có ba nghiệm phân biệt, giá trị thích hợp của tham số m là 9 9 A.    0.   m  0  m  .  m  4 m B. 2 1. C. 4 D. 1 2.
Câu 29: Tập ngiệm của bất phương trình: x x   2
5  2(x  2) là: A. – ( ;  1)  ( ; 4 ). B. 1; 4. C. (1;4) . D. – ( ;  1] [ ; 4 ).
Câu 30: Tập nghiệm của bất phương trình 5x  3  2 là.  3  1   1  A. S    1; 
. B. S   ; . S 1; . S ; .  C.    D.       5  5   5 
Câu 31: Phương trình sau có bao nhiêu nghiệm:  x  4 x  3  0 A. 0 B. 3 C. 1 D. 2
Câu 32: Hỏi tập hợp nào là tập hợp rỗng trong các tập hợp sau? A.  2
x Q x  4x  2   0 . B.  2
x R x  4x  3   0 .
C. x Z x   1 D.  2
x Z 6x  7x 1   0 .
Câu 33: Cho đường thẳng d : 3x – 4 y – 12  0. Phương trình các đường thẳng qua M 2; –  1 và tạo với d một góc là 4
A. 7x – y 15  0; x  7 y – 5  0 .
B. 7x y 15  0; x – 7 y – 5  0 .
C. 7x – y –15  0; x  7 y  5  0 .
D. 7x y –15  0; x – 7 y  5  0 .
x  2  5t
x  7  5t
Câu 34: Xác định vị trí tương đối của hai đường thẳng  :  : 1  và 2  . y  3   6t y  3    6tA. Trùng nhau. B. Song song nhau. C. Vuông góc nhau.
D. Cắt nhau nhưng không vuông góc.
Câu 35: Phương trình tổng quát của đường thẳng đi qua ( A 2; )
1 , B2;5 là:
A. x  2  0.
B. x  2  0.
C. x y 1  0.
D. 2x  7 y  9  0.
Câu 36: Mệnh đề nào sau đây sai?
Trang 03 - Mã đề 132 - https://toanmath.com/ a ba b A.
a c b d . B.   ac bd . c dc d  a b C.
a c b d .
D. ac bc a b . c  0 c d  2 x 16  0 
Câu 37: Hệ bất phương trình 
có số nghiệm nguyên là  x  2  2
2x  7x  5  0  A. 4. B. 2. C. Vô số. D. 3. 
Câu 38: Phương trình tổng quát của đường thẳng đi qua M(2;-1) và có vectơ chỉ phương u  3;7 là:
A. −3x + 7y + 13 = 0. B. 7x + 3y +13 = 0. C. 3x + 7y + 1 = 0. D. 7x + 3y −11 = 0.
Câu 39: Gọi x , ( 1 2
x là hai nghiệm của phương trình 2 2
2x  2mx m  2  0 m là tham số). Tìm giá trị lớn nhất
P  2x x x x  4 . m P của biểu thức ax 1 2 1 2 23 25 9 A. P  . P  . P  . P  8. max 4 B. max 4 C. max 4 D. max
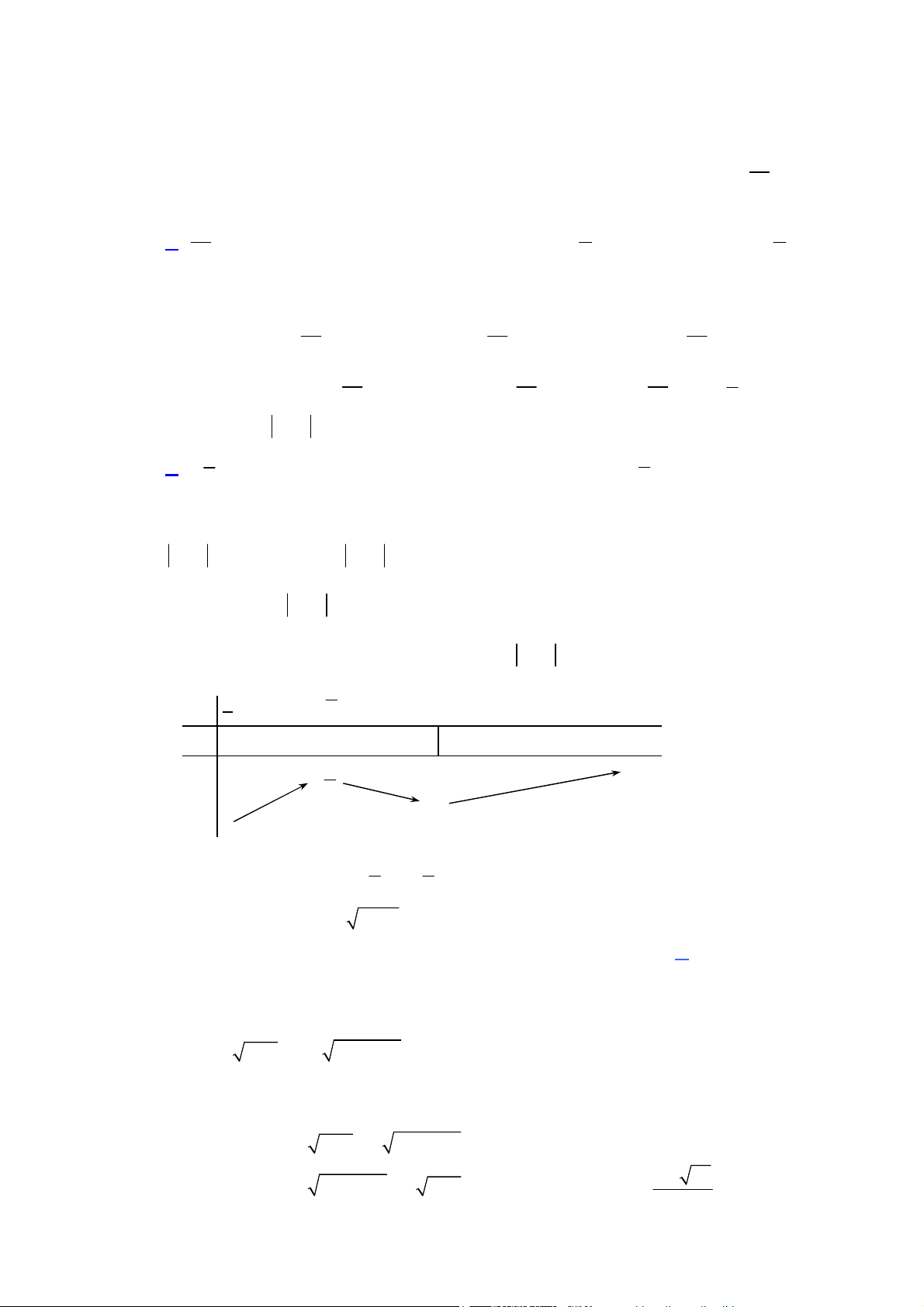
Câu 40: Cho hàm số có bảng biến thiên như sau: x   3 7   2   y   -1
Hàm số đồng biến trên khoảng nào sau đây? A.  ;  7 . B.  ;  2 và  1  ;  . C.  7 ; 3 . D.   3 ;  và   ; 7 .
Câu 41: Xác định dạng của tam giác ABC biết : r r r r . ( r là độ dài bán kính đường tròn nội tiếp c a b
tam giác ABC; r r r tương ứng là độ dài bán kính các đường tròn bàng tiếp các góc A, B, C) a , b , c
A. Tam giác cân đỉnh B
B. Tam giác vuông cân đỉnh B
C. Tam giác vuông đỉnh A
D. Tam giác vuông đỉnh C
Câu 42: Cung tròn có số đo là 5 . Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây. 4 A. 15. B. 172 . C. 225 . D. 5 . Câu 43: Cho A
BC có A2;  
1 , B4;5, C  3
 ;2 . Viết phương trình tổng quát của đường cao CH .
A. 2x  6 y  5  0 .
B. x  3 y  3  0 .
C. 3x y  11  0 .
D. x y 1  0 .
Câu 44: Đường tròn 2 2
x y  6x 8y  0 có bán kính bằng
A. 5. B. 25. C. 10 . D. 10. Câu 45: Cho 2
sinx  cos x  .Khi đó giá trị của biểu thức P = sinx  cos là 3 x 14 2 14 3 A. . . . . 3 B. 3 C. 9 D. 2
Câu 46: Cho tam giác có ba cạnh lần lượt là 5 , 12 , 13 . Khi đó diện tích tam giác bằng : A. 60 . B. 30 . C. 34 . D. 7 5 .
Câu 47: Tọa độ đỉnh I của parabol  P 2
: y  x  4x là: A. I 1;  3 .
B. I 2; 4 . C. I  1  ; 5 . D. I  2  ; 12 .
Câu 48: Tập hợp các giá trị thực của m để bất phương trình ( 2 m  2) 2
x  2(m  2)x  2  0 nghiệm đúng với x   R là.
A.  ;4   ; 0 . B.  0 ; 4 . C. 0; ) . D.  0 ; 4 .
Câu 49: Có bao nhiêu giá trị m nguyên để bất phương trình 2
(m 1)x  2(m 1)x  3  0 vô nghiệm.
Trang 04 - Mã đề 132 - https://toanmath.com/ A. 2. B. 1. C. 4. D. 3.
Câu 50: Phương trình  2 x   3 2
2  5 x 1 có bao nhiêu nghiệm. A. 0 B. 3 C. 1
D. 2---------------------------
-------------------- HẾT ----------
Trang 05 - Mã đề 132 - https://toanmath.com/ 132 1 C 132 11 D 132 21 D 132 31 C 132 41 D 132 2 B 132 12 A 132 22 D 132 32 A 132 42 C 132 3 A 132 13 B 132 23 C 132 33 C 132 43 B 132 4 D 132 14 B 132 24 C 132 34 D 132 44 A 132 5 C 132 15 A 132 25 B 132 35 A 132 45 A 132 6 C 132 16 A 132 26 D 132 36 B 132 46 B 132 7 A 132 17 C 132 27 D 132 37 B 132 47 B 132 8 B 132 18 A 132 28 A 132 38 D 132 48 A 132 9 B 132 19 A 132 29 D 132 39 B 132 49 C 132 10 C 132 20 A 132 30 C 132 40 D 132 50 D
HƯỚNG DẪN MỘT SỐ CÂU KHÓ
Câu 1. Để đo chiều cao một cây ở góc sân trường người ta thực hiện đặt giác kế ở hai vị trí A và B như
hình vẽ để ngắm. Biết khoảng cách AB  (
3 mét) , độ cao ngắm của giác kế so với mặt đất là CH  ,
1 2(mét) và các góc ngắm 0 0
 55 ,  37 .
Chiều cao của cây (làm tròn đến mét) là. A. 4 mét. B. 5 mét. C. 6 mét. D. 7 mét. Lời giải Chọn C D
 55o 37o 18o A DB   
Theo định lý Sin cho tam giác ABD ta có A B AB AD 55o 37o  H SinD Sin37o 3m A . B Sin37o 3.Sin37o 1,2m  AD   SinD Si 18o n C A1 B1  5,843(m).
Đường thẳng đi qua B, A , H vuông góc với HD
Nên AHD vuông tại H và HD = AD.Sin 55o  28,451.Sin 49o  4,786 (m).
Chiều cao của cây là: CD HD+HC  4,786 +1,2  5,986  6(m).
Câu 2. Xác định dạng của tam giác ABC biết rằng r r r r c a b
( r là độ dài bán kính đường tròn nội tiếp tam giác ABC; r r r tương ứng là độ dài bán kính các đường a , b , c
tròn bàng tiếp các góc A, B, C)
A. Tam giác cân đỉnh B
B. Tam giác vuông đỉnh C
C. Tam giác vuông đỉnh A
D. Tam giác vuông cân đỉnh B Lời giải
Trang 06 - Mã đề 132 - https://toanmath.com/ Chọn B
Ta có S pr  ( p a)r p b r p c r a ( ) b ( ) c S S S S 1 1 1 1
r r r r         c a b p c p p a p b p c p p a p b
p( p c)  ( p a)( p b)  p(a b c)  ab 2 2
 (a b c)(a b c)  2ab  (a b)  c  2ab 2 2 2
a b c
Vậy tam giác ABC là tam giác vuông đỉnh C
Câu 3. Tập nghiệm của bất phương trình 2 x  2 x  5  x  3 là: A.  ;
 2  4  5; . B. ;  1 . C.  ;  2 6; . D. 100;2 . Lời giải Chọn A x   3  0 x   3  2  
x  2 x  5  0 x     ;2  5; Ta có:     
2x  2x  5  x  3   x  3 0    x  3    2   
x  2 x  5 2 2
x  6x  9  x    8x 11  0 x   3 x   ;  2 5;   x    ;  2     x  3
x 4  5;      x  
;4 54 5;   
Vậy tập nghiệm của bất phương trình là: S   ;
 2  4  5; .
Câu 4. Cho đường tròn 2 2
(C) : x  y  4x  6y  5  0. Đường thẳng d đi qua A(3; 2) và cắt (C) theo
một dây cung ngắn nhất có phương trình là
A. x y 1  0 .
B. x y  1  0 .
C. 2x y  2  0 .
D. x y 1  0 . Lời giải Chọn A N H A M I . f x y 2 2 ;
x y  4x  6y  5.
f (3; 2)  9  4 12 12  5  6  0.
Vậy A3; 2 ở trong C. Đường tròn (C) có tâm I(2; 3).
Trang 07 - Mã đề 132 - https://toanmath.com/
Dây cung MN ngắn nhất  IH lớn nhất  H A MN có vectơ pháp tuyến là  IA  1;  
1 . Vậy d có phương trình: 1(x  3) 1( y  2)  0  x y 1  0 .
Câu 5. Cho hình vuông ABCD cạnh a . Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm   2 a
M , N , P, Q sao cho AM BN CP DQ x (0  x a) . Nếu PM . DC  thì giá trị của 2 x bằng: 3a a a A. 4 . B. a . C. 4 . D. 2 . Lời giải Chọn A   2
   2
    2 Ta có: . a a a PM DC   PQ PN .  P . Q DC PN. 2   DC  2 DC  2
    2 2 a 2 a 3  .  . a PD DC PC DC   (a x) 2  2 2 a xa  2
ax a  2  x  . 4 a
Câu 6. Phương trình x  2 (x 1)  m  0 có ba nghiệm phân biệt, giá trị thích hợp của tham số m là 9 9 A.    0.   m  0  m  .  m  4 m B. 2 1. C. 4 D. 1 2. Lời giải Chọn A
x  2 (x 1)  m  0  x  2 (x 1)  m 2 
x x  2 , x  2
Xét hàm số y x  2 x   1   2
x x   2 , x  2
Suy ra bảng biến thiên của hàm số y f x  x  2 x   1 như sau: 1 x ∞ 2 2 +∞ 2 2 x x  2 x x  2 9  f(x) 4 0  Yêu cầu bài toán 9 9
0  m     m  0. 4 4
Câu 7. Phương trình  2 x   3 2
2  5 x 1 có bao nhiêu ngiệm. A. 0 B. 3 C. 1 D. 2 Lời giải Chọn D ĐK: x  1
Đặt u x 1 ; 2 v x x  1 (u;v  0) . PT trở thành: u  2 2 2 2(  )  5 v u v uv  v   2u + Với 2 u  2v
x 1  2 x x 1 (vô nghiệm) + Với 2  v  2u
x x  1  2 x 1 2 5 37
x  5x  3  0  x  (tmđk). 2
Trang 08 - Mã đề 132 - https://toanmath.com/
Câu 8. Cho các số thực x, y, z thỏa mãn x + y + z = 0, x2 + y2 + z2 = 8. Tìm giá trị nhỏ nhất của biểu thức
P x y z 5 A. 4 B. 5 C. 3 D. 4 Lời giải Chọn A
P   x y z 2 2 2 2 2
x y z  2 x y y z z x  2 2 2 2
P x y z x y z   y z x   z x y
Áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối ta có           2 y z y z x x x y z x
Chứng minh tương tự y z x  2  y
z x y  2 ,  z Vì vậy 2 P   2 2 2
2 x y z  Thay 2 2 2 2
x y z  8  P  16  P  4
Dấu bằng có thể xảy ra, khi x, y, z  2; 2
 ;0 hoặc các hoán vị, ta có P = 4 Vậy min P = 4
Câu 9. Cho đường thẳng d : 3x – 4 y – 12  0. Phương trình các đường thẳng qua M 2; –  1 và tạo với d một góc là 4
A. 7x – y 15  0; x  7 y – 5  0 .
B. 7x y 15  0; x – 7 y – 5  0 .
C. 7x – y –15  0; x  7 y  5  0 .
D. 7x y –15  0; x – 7 y  5  0 . Lời giải Chọn C  Gọi n   ; A B  và 2 2
A B  0 là véctơ pháp tuyến của  3A 4 Ta có: B 2 2 cos 
 2 3A  4B  5 A B 2 2 2 2 4
3  4 . A BB  7 2 2  7  48  7  0 A A AB B   A   7  B
Với B  7A chọn A 1, B  7  x  7y  5  0 Với A  7
B chọn A  7, B  1
  7x y 15  0 .
Câu 10. Có bao nhiêu giá trị của a để phương trình 2 2
2x  3x  2  5a  8x x có nghiệm duy nhất. A. 0 B. 3 C. vô số D. 1 Lời giải Chọn D
Phương trình tương đương với 2 2
2x  3x  2  x  8x  5a  2 1 3 
x  5x  2, x , 2    ,    3   Xét hàm số 2 2 
y f (x)  2x  3x  2  x  8x   2  1 
x 11x  2, x  2,   3    
Suy ra, bảng biến thiên của hàm y f x 2 2
 2x  3x  2  x  8x như sau:
Trang 09 - Mã đề 132 - https://toanmath.com/ Yêu cầu bài toán 49 49
5a   12  a   . 60
Câu 11. Cho hai đường thẳng d : 2x y  3  0 và  : x  3 y  2  0 . Phương trình đường thẳng d ' đối
xứng với d qua  là:
A. 13x 11y  2  0 .
B. 11x  2 y  13  0 .
C. 11x  13y  2  0 .
D. 11x  2 y  13  0 . Lời giải Chọn D
Giao điểm của d và  là nghiệm của hệ
2x y  3  0
2x y  3  x  1       A 1  ;  1 .
x  3y  2  0 x  3y  2 y     1
Lấy M 0;3d . Tìm M ' đối xứng M qua  .
Viết phương trình đường thẳng ' đi qua M và vuông góc với  :  ': 3x y  3  0 .
Gọi H là giao điểm của ' và đường thẳng  . Tọa độ H là nghiệm của hệ  7   3  2  0   3  2 x   x y x y   10  7 9        H   ; . 3  x y   3  0
3x y  3 9  10 10   y    10 Ta có  
H là trung điểm của MM ' . Từ đó suy ra tọa độ 7 6 M '  ; . 5   5   
Viết phương trình đường thẳng d ' đi qua 2 điểm A và M ': điểm đi qua A(1;1) , vectơ chỉ   phương  2 11    AM '   ; .
5 5   vectơ pháp tuyến 11 2 n  ;      5 5  11 2 d ' :  x   1   y  
1  0  11x  2y 13  0 . 5 5
Câu 12. Gọi x , ( 1 2
x là hai nghiệm của phương trình 2 2
2x  2mx m  2  0 m là tham số). Tìm giá trị lớn nhất
P  2x x x x  4 . m P của biểu thức ax 1 2 1 2 25 9 23 A. P  8. P  . P  . P  . max B. max 4 C. max 4 D. max 4 Lời giải. Chọn B Ta có 2   m   2 m   2 ' 2 2  m  4 .
Phương trình có hai nghiệm khi và chỉ khi 2
 '  4  m  0  2  m  2.   *
Trang 10 - Mã đề 132 - https://toanmath.com/  1 x  2 x  m
Theo định lý Viet, ta có  2  m  2 . 1 x 2 x    2 Khi đó 2
P  2x x x x  4  m m  6  m  2 m  3   m  2 m  3 1 2 1 2       2 2  1  25 25
 m m  6   m  (do 2   m  2 ). 2  4      4 Dấu ' 25
 ' xảy ra khi và chỉ khi 1 m  : thỏa   * . Vậy P  . 2 max 4 2 2
x  4xy y  1 Câu 13. Nếu  ;
x y  là nghiệm của hệ phương trình: 
. Thì xy bằng bao nhiêu ? y  4xy   2 A. 4  . B. 1.
C. Không tồn tại giá trị của xy . D. 4. Lời giải Chọn C
x y2 1  2xy Ta có : 2 2
x  4xy y  1   .
x y 2  1 6xy
y  4xy  2  2 y  8xy  4   x y   x y  8xy  4  0 2 2  1   1  3
  x y   x y2   x y   x y2  2  0  x y   x y        0 không có  2   2  2
giá trị của x , y thỏa nên không tồn tại xy .
Trang 11 - Mã đề 132 - https://toanmath.com/
Document Outline

  • TestA_15
  • TestB_15
  • TestC_15
  • TestD_15
  • MTBlankEqn_2
  • TestHDG_15
  • TestHDG_3
  • TestQ_15
  • TestQ_3