Đề thi KSCL Toán 11 năm 2017 – 2018 trường Thạch Thành 1 – Thanh Hóa lần 2

TRƯỜNG THPT THẠCH THÀNH I
KỲ THI KHẢO SÁT CHẤT LƯỢNG LẦN 2 TỔ TOÁN- TIN NĂM HỌC: 2017- 2018 Môn thi: TOÁN Thời gian: 120 phút
Câu 1: (2 điểm) Cho hàm số: 2
y  x  x  2 P và đường thẳng: d : y  x  m
1. Khảo sát sự biến thiên, vẽ đồ thị (P) của hàm số.
2. Tìm m để đường thẳng d cắt (P) tại hai điểm phân biệt A, B sao cho AB  10 .
Câu 2: (2 điểm)
1. Giải phương trình: 3 sin 3x  sin x  2.cos .
x cos 2x  0 .
2. Một hộp đựng 7 bi đỏ, 8 bi xanh. Lấy ngẫu nhiên ra 5 viên bi. Tính xác suất để lấy được 5
viên bi có đủ cả hai màu.
Câu 3: (1,5 điểm) 12
1. Tìm số hạng không chứa x trong khai triển Niu-tơn của nhị thức:    2 2  P x  x    .  x  3    2. Tính giới hạn: 5 4x 7 6x lim . 3 2 x 1 
x  x  x 1
Câu 4: (1 điểm) Tìm m để đồ thị hàm số: 4
y  x   m   2 3
1 x  2m  3 cắt trục hoành tại 4
điểm phân biệt có hoành độ lập thành một cấp số cộng.
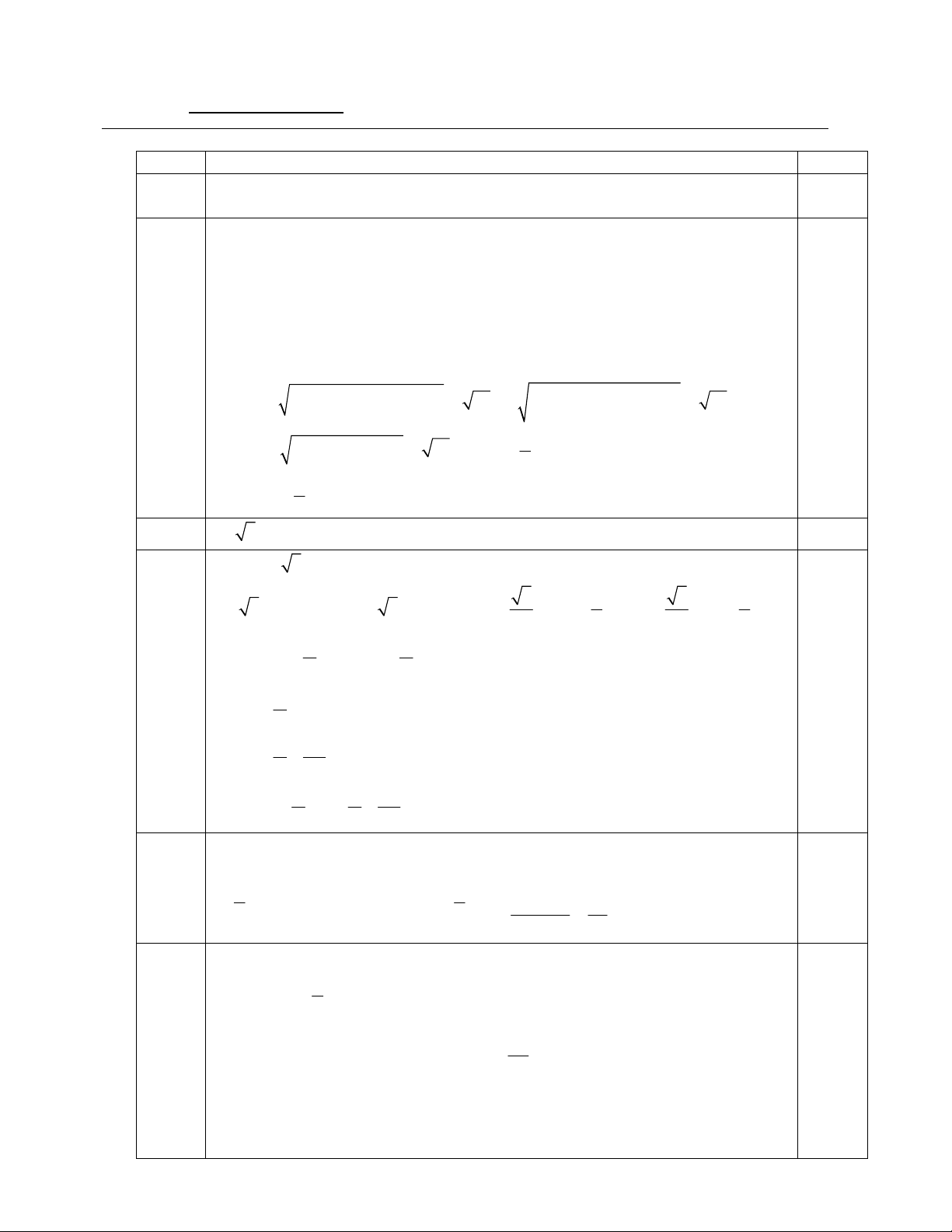
Câu 5: (1,5 điểm) Cho đường tròn C x  2   y  2 : 2
3  25 và điểm M 7;3 .
1. Tìm phương trình đường tròn C ' là ảnh của đường tròn C qua phép vị tự tâm J 3;  1 tỷ số k  3  .
2. Viết phương trình đường thẳng d đi qua M cắt C tại hai điểm phân biệt A, B sao cho
AB  7 và diện tích tam giác IAB bằng 12. (với I là tâm của đường tròn C  ).
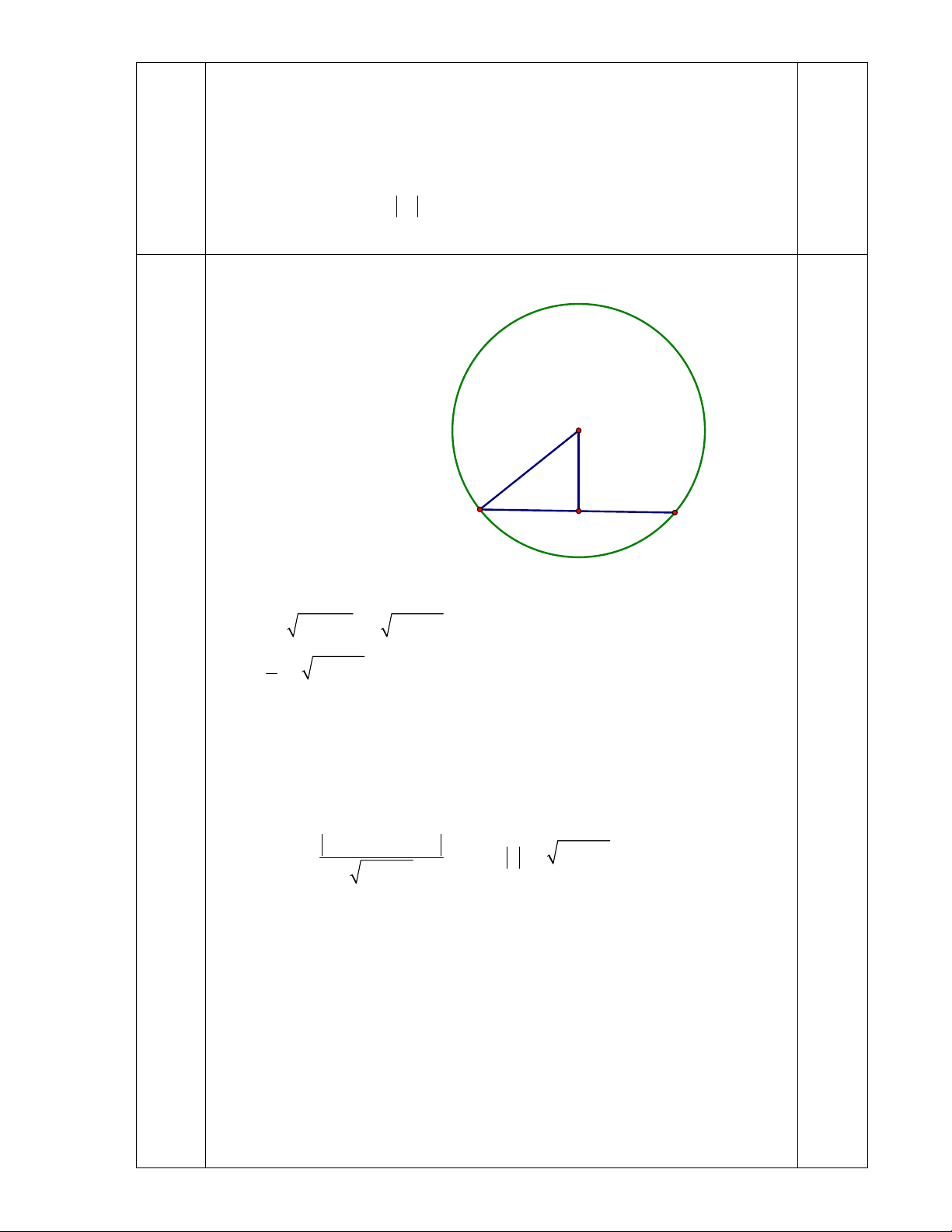
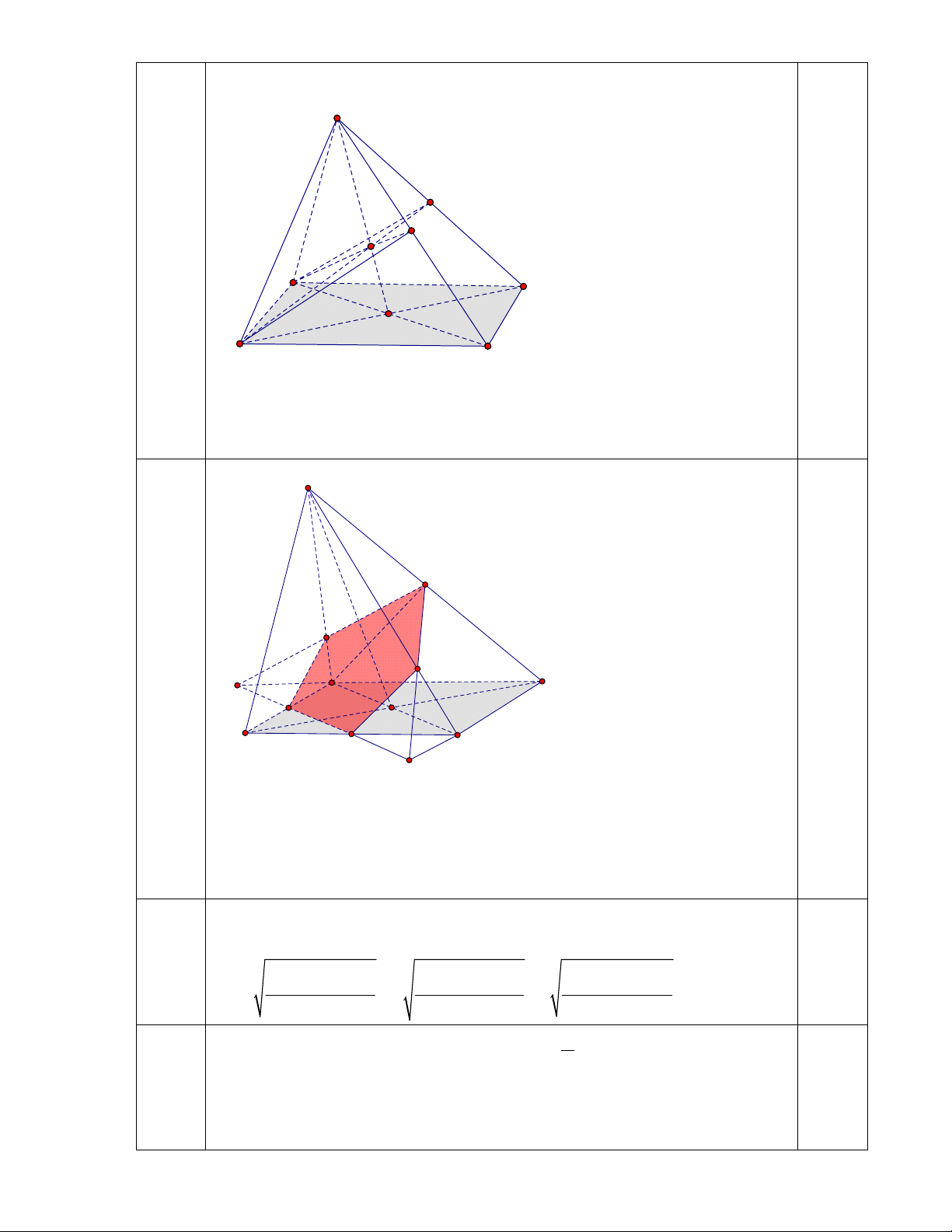
Câu 6: (1,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P
lần lượt là trung điểm của SC, AB, AD.
1. Tìm giao điểm của SD với mặt phẳng (ABM).
2. Dựng thiết diện của hình chóp với mặt phẳng (MNP).
x, y, z  0
Câu 7: (0,5 điểm) Cho 
. Tính giá trị của biểu thức:
xy  yz  zx 1  2 1 y  2 1 z   2 1 z  2 1 x   2 1 x  2 1 y  S  x  y  z 2 2 2 1 x 1 y 1 z
----------------------------------Hết---------------------------------------
(Cán bộ coi thi không giải thích gì thêm)
Họ, tên thí sinh:....................................................... Cán bộ coi thi:........................................
TRƯỜNG THPT THẠCH THÀNH I
KỲ THI KHẢO SÁT CHẤT LƯỢNG LẦN 2 TỔ TOÁN- TIN NĂM HỌC: 2017- 2018
Môn thi: TOÁN Thời gian:120 phút ĐÁP ÁN Câu Đáp án Điểm
Câu 1 1. + TXĐ, vẽ đúng bảng biến thiên 0,5 + Vẽ đúng đồ thị. 0,5
2. Phương trình hoành độ giao điểm: 2 2
x  x  2  x  m  x  2x  m  2  0  1
Để đường thẳng (d) cắt (P) tại 2 điểm phân biệt thì pt(1) có 2 nghiệm phân
biệt:   '  0  m  3  0  m  3  2 x  x  2 Giả sử: A 1 x ; 1
x  m; B 2 x ; 2
x  m với 1 2   1 x . 2 x  m  2
x  x 2 x  x 2  10  2x  x 2   2 1 2 1 1 2  4 1 x 2 x  10   Từ gt    m  7 2 4 4
2  10  m   t / m2 4 7 KL: m   4
Câu 2 1. 3 sin3x sin x  2.cos .xcos2x  0 (1) Pt  
1  3 sin 3x  sin x  cos3x  cos x  0 3 1 3 1
 3 sin 3x  cos3x  3 sin x  cos x 
sin 3x  cos3x 
sin x  cos x 2 2 2 2        sin 3x   sin x  0,5      6   6    x   k  6     k x    4 2   k 
KL :T    k; 0,5 x    6 4 2 
2. Gọi A là biến cố cần tìm. Ta có: n 5  0,5 15 C C  C 38 n  A 5 5  0,5 7 C  8
C  P  A 1 P A 5 5 7 8 1  5 C 39 15
Câu 3 1. Tìm số hạng không chứa x trong khai triển Niu-tơn của nhị thức: 12    2 2  P x  x     x  . 12 k  2 k k  0,5 Số hạng tổng quát:   C   2x   2    k k C  123k k T 1 12 12 x  x 
Số hạng không chứa x ứng với:12  3k  0  k  4
Vậy só hạng không chứa x là:  2  4 412 C  7920 0,5 2. 3
5  4x  7  6x
5  4x  2x  3 2x 3 3  7  6x lim  lim  lim 3 2 3 2 3 2 0,25 x 1 
x  x  x 1 x 1 
x  x  x 1 x 1 
x  x  x 1 2 4
 x 8x  4  lim 
x  x  2 1 1  x  
1  5 4x  2x  3 3 2
8x  36x  48x  20 lim x 1     x  2 1  x  
1 2x  32  2x  3 3 3
7  6x  7  6x2    4   lim x 1   x  
1  5 4x  2x  3   8x 20 lim x 1     x   1
2x  32  2x  3 3 3
7  6x  7  6x2    4  12 0,25      2  .2  2   1 .3 Câu 4 4
y  x  3m   2  
1. Để đồ thị hàm số: 1 x
2m 3 cắt trục hoành tại 4 điểm
phân biệt có hoành độ lập thành một cấp số cộng thì phương trình: 4
x   m   2 3
1 x  2m  3  0 
1 có 4 nghiệm phân biệt lập thành một cấp số cộng. Đặt 2
t  x t  0 pt trở thành: 2
t  3m  
1 t  2m  3  02 0,25
Pt(1) có 4 nghiệm phân biệt khi pt(2) có hai nghiệm dương phân biệt        
m     m   2 2 9m 2m 11 0 3 1 4 2 3  0     1 11
 S  3m 1 0  m    m  3 3 9 P 2m 3 0       3 m   0,25  2
Gọi 1t;t2 là hai nghiệm của (2): 0  1t  t2 . Khi đó 4 nghiệm lập thành cấp số cộng của pt(1) là: 1
x   t2  2
x   1t  3 x  1t  4 x  t2  3 x  2 x  4 x  3
x  2 1t  t2  1t  t2  3 1t  t2  9 1t 0,25  3m 1 1 t   10 t2  9 1t    93m   1
 1t  t2  3m 1  t  2  10
t .t 2m 3    Khi đó:  1 2 3m   1 93m   1  .  2m  3  10 10 m  3 2 81m 146m 291 0       97 m    81
Đối chiếu với ĐK (3)  m  3 KL:   3 m T  0,5
Câu 5 1. Đường tròn C x  2   y  2 : 2 3
 25 có tâm I 2; 3
  bán kính R  5 I ' ; x y   V là tâm của (C’)
J ;k  I    x  3  3    1 x  6  JI '  3  JI      I '6;13 0,5 y 1  3    4   y 13
Bán kính của C ' : R '  3  .R  3.5 15 0,25
Phương trình C  x  2   y  2 ' : 6 13  225 2. I h A H B
Gọi H là hình chiếu của I trên , H là trung điểm AB. Đặt IH  , h h  0 2 2 2
 AB  2 R  h  2 25  h 2 1   2 2 4 4 2 h 9 S  .2 h
25  h  12  25h  h  144  h  25h 144  0 IAB   2 2  h 16 TH1: 2
h  16  h  4  AB  6  7  loại. 0,5 TH: 2
h  9  h  3  AB  8  7  thỏa mãn.  d I;d  3
Phương trình của đường thẳng d : a x  7  b y  3  0
 ax  by  a  b   2 2 7 3
0 a  b  0 
a  b  a  b d I; d  2 3 7 3 2 2  3 
 3  5 a  3 a  b 2 2 a  b   2 2 4a 3b
 16a  9b  4a   3  b + 4a  3 .
b Chọn a  3  b  4  d : 3x 4 y 9  0
+ 4a  3b . Chọn a  3  b  4
  d : 3x  4y  33  0 0,25 KL: Câu 6 1. S M J I B C O A D
Gọi O  AC  BD Trong
mp SAC : AM  SO  I 1,0
Trong mp SBD : BI  SD  J  J  SD  ABM  S M K H B C F N O A P D E
2. Trong mp  ABCD : NP CD  E; NP BC  F Trong
mp SBC : FM  SB  K
Trong mp SCD : EM  SD  H 1,0
Nối NK; PH ta được nguc giác MHPNK là thiết diện cần dựng. Câu 7
x, y, z  0 
Cho xy  yz  zx 1 . Tính giá trị của biểu thức:  2 1 y  2 1 z   2 1 z  2 1 x   2 1 x  2 1 y  S  x  y  z 2 2 2 1 x 1 y 1 z   Đặt 
x  tan a; y  tan ;
b z  tan c 0  a,b,c     2  Giả thiết suy ra: tan .
a tan b  tan .
b tan c  tan . c tan a  1
 tan atan b  tan c 1 tan . b tan c tan b  tan c 1     
 tan b  c  cot a  tan  a   1 tan . b tan c tan a  2   
 b  c   a  k  a  b  c  2 2  2 1 y  2 1 z   2 1 tan b 2 1 tan c cos a x  tan a  tan a 2 2 1 x 1 tan a cos . b cos c sin a
cosb  c cos .
b cos c  sin . b sin c    1 tan . b tan c cos . b cos c cos . b cos c cos . b cos c  1 yz
Tương tự:  S  1 yz 1 zx 1 xy  3   xy  yz  zx  31  2
Học sinh là theo cách khác, nếu đúng vẫn cho điểm tối đa của câu đó.