Đề thi Olympic 27/4 Toán 10 năm 2017 – 2018 sở GD và ĐT Bà Rịa – Vũng Tàu

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI OLYMPIC 27/4 - NĂM HỌC 2017- 2018
TỈNH BÀ RỊA – VŨNG TÀU
MÔN THI: TOÁN LỚP 10
ĐỀ THI CHÍNH THỨC Ngày thi: 06/03/2018
Thời gian làm bài: 180 phút, không kể thời gian giao đề Câu 1 (6,0 điểm): 1) Giải phương trình 2
x  3 + x  2 = x  3x  2 3 3 2 2
x  y  x  y  xy 1 y  x
2) Giải hệ phương trình  2
 2x  y  3x  2y  2  3x  y  4  Câu 2 (4,0điểm):
1) Cho tam giác ABC có diện tích S và bán kính của đường tròn ngoại tiếp R thỏa mãn hệ thức 2 2 S = R  3 3 3
sin A  sin B  sin C . Chứng minh tam giác ABC là tam giác đều. 3
2) Cho tam giác ABC đều có độ dài cạnh bằng 3. Trên các cạnh BC, ,
CA AB lần lượt lấy các
điểm N, M , P sao cho BN  1, CM  2, AP  x (0  x  3).   
a) Phân tích véc tơ AN theo hai vectơ AB, AC.
b) Tìm giá trị của x để AN vuông góc với PM .
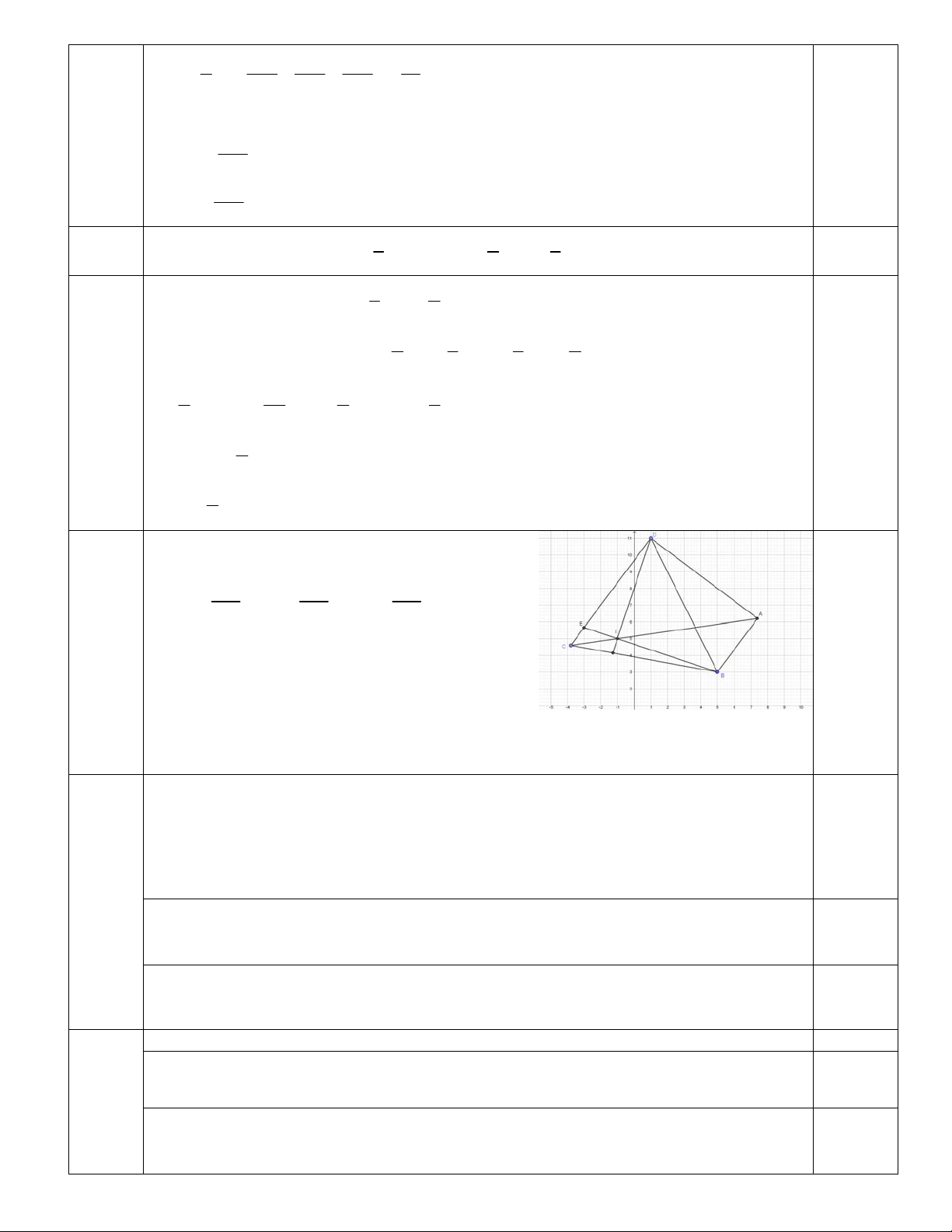
Câu 3 (2,0 điểm): Trong mặt phẳng tọa độ Oxy , cho hình thang ABCD vuông tại , A D và 3
AD  CD  2AB . Điểm I thuộc đoạn AC sao cho AI  AC. Biết điểm B(5;3), đường thẳng DI 4
có phương trình 3x  y  8  0 và điểm D có hoành độ dương. Tìm tọa độ điểm . D
Câu 4 (3,0 điểm): Cho phương trình 2
x   m   2 4
1 x  3m  2m  0 (m là tham số).
1) Tìm tất cả các giá trị nguyên của m để phương trình có hai nghiệm phân biệt x , x thỏa mãn 1 2 3 3 x  x  18. 1 2
2) Tìm tất cả các giá trị nguyên của m nguyên sao cho phương trình đã cho có nghiệm nguyên.
Câu 5 (3,0 điểm): Cho 4 số thực dương a, ,
b c,d thỏa mãn a  b  c  d  4 . Chứng minh rằng: a b c d     2 . 2 2 2 2
1 b c 1 c d 1 d a 1 a b
Câu 6 (2,0 điểm): Cho 2018 số nguyên dương phân biệt và nhỏ hơn 4034. Chứng minh tồn tại 3 số
phân biệt trong 2018 số đã cho mà một số bằng tổng hai số kia.
----------------- HẾT -----------------
Họ và tên thí sinh............................................................................ Số báo danh ..................................
Chữ ký của giám thị 1 ....................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI OLYMPIC 27/4 - NĂM HỌC 2017- 2018
TỈNH BÀ RỊA – VŨNG TÀU
MÔN THI: TOÁN LỚP 10
HƯỚNG DẪN CHẤM ĐỀ THI CHÍNH THỨC
(Hướng dẫn chấm có 04 trang) Câu Nội dung Điểm Câu 1
1) Đk x  3 0,5 6,0 2 2 2
x  3 + x  2 = x  3x  2  x  3  x  2  2 x  5x  6  x  3x  2 điểm 2 2 2 2
 x  5x  3  2 x  5x  6  0  x  5x  6  2 x  5x  6  3  0 2x0,25 Đặt 2
t  x  5x  6, t  0. Ta được pt : 2
t  2t  3  0 2x0,25 t  1(l 2x0,25 2
 t  2t  3  0   t  3(n) 2 2
t  3  x  5x  6  3  x  5x  3  0 0,5  5  37 x  (l) 5  37 2
. KL pt có nghiệm là x    2 0,5  5  37 x  (n)  2 3 3 2 2
x  y  x  y  xy 1 y  x (1)  2
 2x  y  3x  2y  2  3x  y  4 (2)  3 3
(1)  (x 1)  3(x 1)  y  3y 0,25 2 2
 (x 1 - y) x  xy  y + 1  0    y  x 1 0,25   2 2
x  xy  y + 1 = 0 Ta có 2 2
x  xy  y + 1 = 0 vô nghiệm 2x0,25 0,25
Với y = x + 1 thay vào pt (2) ta được pt: 2
3x 1 + 3x  4  3x  x  3 2
( 3x 1 - (x 1)  ( 3x  4  (x  2)  3x  3x 2 2 x  x 0,25   x  x 2  3x  3x
3x 1  x 1
5x  4  x  2 0,25  1 1  2  (x  x)   3  0  
 3x 1  x 1
5x  4  x  2  0,25 2 x  x  0  2x0,25  1 1 1   
 3  0 (vn vi : x  )
 3x 1  x 1
5x  4  x  2 3 0,25 x  0   x 1 0,25
KL: Hpt có nghiệm là (0; 1), (1; 2). Cầu 2 3 3 3 a B c 2x0,25 3 3 3 4điểm
1) Theo định lí sin ta có : sin A  ; sin B  ;sin C  3 3 3 8R 8R 8R 2x0,25 3 3 3 2  a b c  1 2 3 3 3 VT = R     
R(a  b  c ) 3 3 3 3  8R 8R 8R  12 2x0,25
Áp dụng bắt đẳng thức cô – si ta có: 3 3 3
a  b  c  3abc  abc VT  4R 2x0,25 abc Mà S 
, dấu “ =” xảy ra khi và chỉ khi a = b = c  ABC đều 4R   
 1   2  1  0,25x2
2) a) AN = AB  BN = AB   AC  AB  AB + AC 3 3 3    1  x  0,25
b) Ta có PM = PA  AM  AC - AB 3 3  
 2  1    1  x  
AN  PM  AN.PM  0  AB  AC . AC  AB  0     0,25  3 3   3 3 
2   2x 2
x   1 2  . AB AC  AB  .
AB AC  AC  0 9 9 9 9 2x0,25 x
 1 2x  1  0 2 0,25 4  x  0,25 5 Câu 3 2,0 Đặt AD = a điểm 2 2 2 5a 5a 5a 0,5 2 2 2 BD = ; DI = ; MI  4 8 8
Suy ra BDI vuông cân tại I.
Do đó BI : x  3y 14  0. 0,5 0,25
Mà I là giao điểm của BI và DI  I(-1; 5). 0,25
Vì D  DI  D(x; 3x + 8) mà DI = BI x 1(n ) 2 2
 (x 1)  (3x  3)  40   D(1;11) x  3(  l) 0,25x2
   m  2   2 m  m 2 4 1 4 3 2
 4m 1  0, m   R . 0,5
Suy ra phương trình luôn có 2 nghiệm phân biệt x , x . Theo viet ta có 1 2
x  x  4m 1 1 2  2
x .x  3m  2m  1 2
x  x   x  x   x  x 2  3x x   4m   1 4m  2 3 3 1  3 2 3m  2m  0,25 1 2 1 2 1 2 1 2      3 2
 28m 15m  6m 1 3 3 3 2
x  x  18  28m 15m  6m 1  18 0,25 1 2  m   2
1 28m 13m 19  0  m 1
Phương trình có nghiệm nguyên suy ra  là bình phương của 1 số nguyên 0,5 x  0 0,5 Nếu m = 0 thì ta có pt : 2
x  x  0   (thỏa) x  1
Nếu m  0 thì m    k  2 2 4 1 2 1 (k  Z ) do 2 4m 1là số lẻ 0,5 2
 m  k k   1
Mà k, k  
1  1  k,k+1 là hai số chính phương (vô lí). 0,5 Vậy chỉ có m =0 thỏa 2 2 a ab c ab c ab c 0,5 Ta có  a   a   a  2 2 1 b c 1 b c 2b c 2 ab c b . a ac 1 1 0,5 Lại có a   a 
 a  ba  ac  a  ab  abc 2 2 4 4 a 1 Vậy  a  ab  abc 2   1 b c 4
Chứng minh tương tự ta có 0,5 b 1 c 1 d 1
 b  (bc  bcd),
 c  (cd  cda),
 d  (da  dab) 2 2 2 1 c d 4 1 d a 4 1 a b 4 a b c d      2 2 2 2
1 b c 1 c d 1 d a 1 a b 1
 a  b  c  d  ab  bc  cd  da  abc  bcd  cda  dab 4 2
 a  b  c  d  0,5
Lại có ab  bc  cd  da  a  cb  d    4    2  4
 1 1 1 1   a  b  c  d  16 0,5
abc  bcd  cda  dab  abcd     .      a b c d   4
 a  b  c  d 1 
a b  c  d 3  4 16 a b c d 0,5 Do đó   
 a  b  c  d  2  2 2 2 2 2
1 b c 1 c d 1 d a 1 a b
Dấu « = » xảy ra  a  b  c  d  1
Cho 2018 số nguyên dương khác nhau và nhỏ hơn 4034. Chứng minh tồn tại ba số 2,0đ
trong 2018 số đó mà một số bằng tổng hai số kia.
Gọi 2018 số nguyên dương đã cho là a , a ,..., a
. Không mất tính tổng quát giả sử 0,25 1 2 2018
1  a  a  ...  a  a  4033. 1 2 2017 2018
Đặt b  a  a i  2,3,.., 2018 i i 1  
Suy ra 1  b  b  ...  b  4032 0,25 2 3 2018
Xét dãy gồm 4034 số a , a ,..., a
,b ,b ,...,b
. Các số này nhận 4033 giá trị khác 0,5 2 3 2018 2 3 2018
nhau nên có ít nhất 2 số trong dãy số trên bằng nhau .
Mặt khác ta có : a  a ;b  b ,i  j (2  i, j  2018) . Ngoài ra 0,5 i j i j
a  b , i
  2,3,...,2018 (do a  0) . Suy ra tồn tại a  b x  y,2  x, y  2018 x y  i i 1
Hay a  a  a  a  a  a (đpcm) 0,5 x y 1 1 x y