
Preview text:
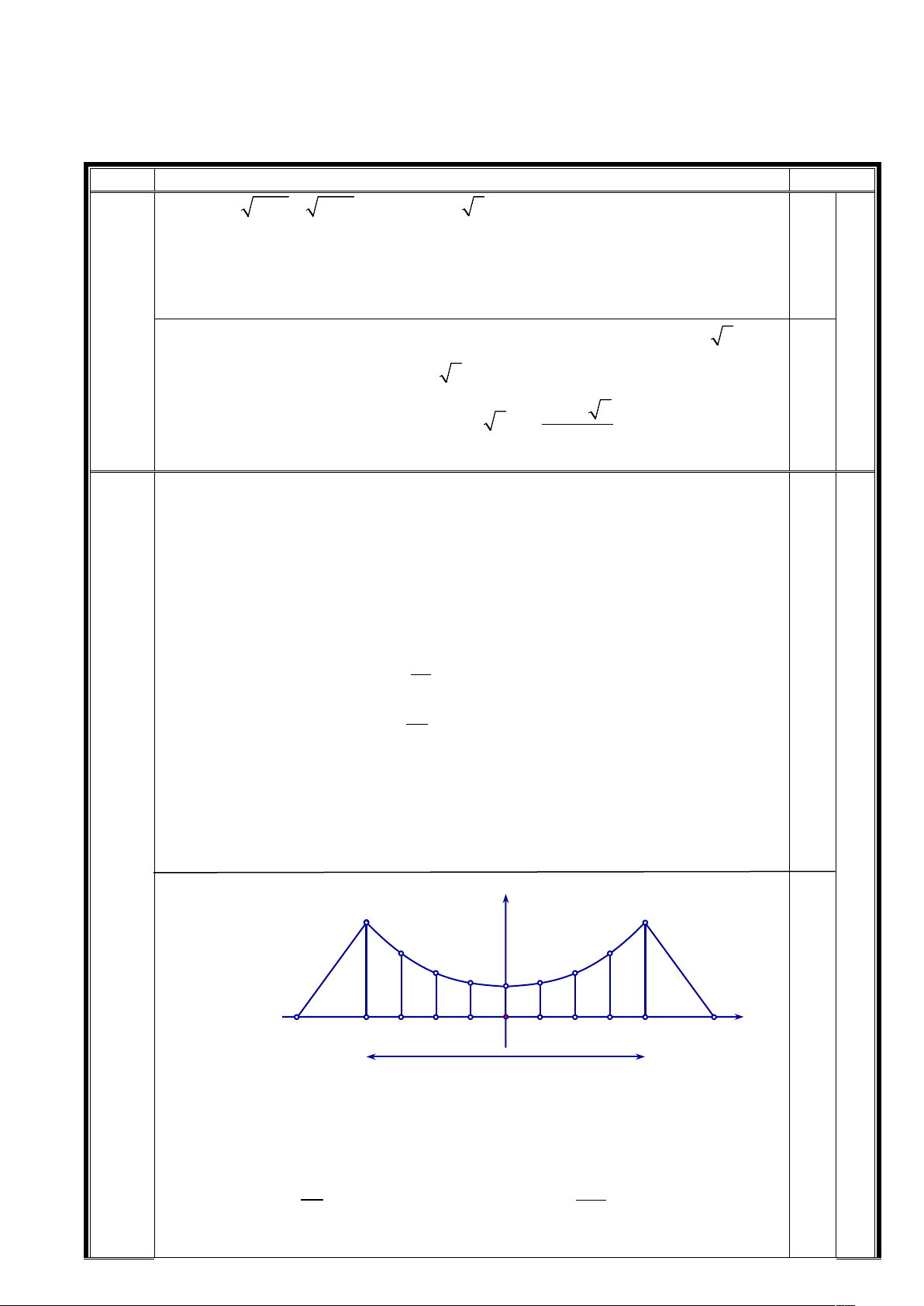
8 - 2019 Câu 1 ( ). 2 x 3 6 x 18 3x x , m (1) , m a) i (1) khi m 3. b) m . Câu 2 (5 4 2 2 3 x x y x y 1 a) . 3 2 x y xy x 1 b) ây truy là Parabol ACB u, cu i c c g m
A , B trên m i tr c AA và BB v cao 30 m . Chi n
A B trên n n c u b ng 200 m .
cao ng n nh t c a dây truy n trên c u là CC ' 5 m. G i Q , P ,
, C’, I , J , K n
thành các ph n b ng nhau. Các thanh th ng n i n n c u v
n: QQ , PP , HH , CC ' , II , JJ , KK g i là các dây cáp treo. Tính t dài c a các dây cáp treo? Câu 3 (4 Cho tam giác ABC M BC a,CA , b AB . c a) Ch minh r 2 2 b c cos A a . c cos C . b cos B . b) Tìm t p h p các i M sao cho 2 2 2 MB MC MA . Câu 4 Tr Oxy, cho (3
A ;1), B( 1; 2) . a) N Ox AN b) M d : y x MA P và MB Q PQ Câu 5
Cho x, y, z : 2 2 2 x y z 4 xyz. x y z 2 xyz. ---------------------- -------------------------
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ THI OLYMPIC TOÁN LỚP 10
Năm học 2018 - 2019 Câu Đáp án Điểm
a) Đặt t = 3 + x + 6 − x Đk : 3 ≤ t ≤ 3 2 . 1.0 t = 1( − l)
Phương trình có dạng: 2t − 2t − 3 = 0 ⇔ = t 3 1.0
Giải ra nghiệm x=-3 và x=6 1.0 ∈ 1,0 6,0
b) (1) có nghiệm khi có phương trình 2
t − 2t = 9 − 2m có nghiệm t 3;3 2 Xét hàm số 2
f (t) = t − 2t với t ∈ 3;3 2
, sử dụng bảng biến thiên ta có ĐK 1.0 Câu 1 phương trình có nghiệm 9 − + 6 2
3 ≤ 9 − 2m ≤ 18 − 6 2 ⇔ ≤ m ≤ 3. 1.0 2 a) Ta có: 4 2 2 2 2 3
x + x y = (x − xy) + 2x . y Đặt 2 3
a = x − xy;b = x y. 1,0 2 a + b = 1 a = 1.
Ta có hệ phương trình: . Suy ra, 2
a − a − 2 = 0 ⇔ −a + b = 1 − a = 2. − 2
x − xy =1 x = 1 ± ⇔ 3 = = x y 0 y 0 1,0 3 2 Khi đó: x + = 2 − 2 x 2
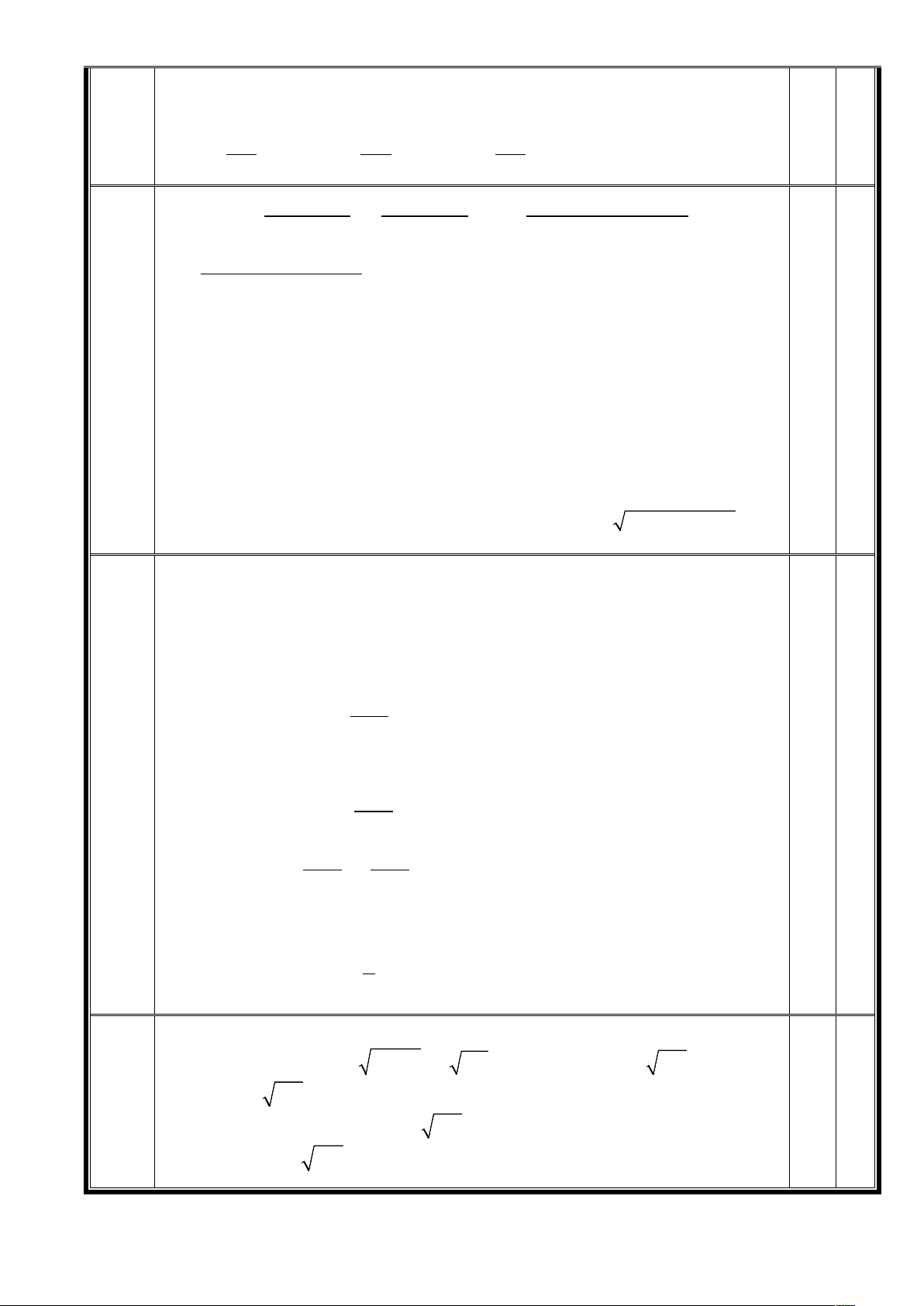
x − xy = 2 − ⇔ (v n). − 3 y = 3 x 3 x y = 2 − 1,0 Câu 2 ( ; x y) ∈ ( { 1;0),( 1 − ;0)} . 5,0 y B A Q K P J H C I y3 30m y2 y1 5m B′ Q′ P′ H ′ O I ′ J ′ K ′ A′ x 200m 1,0
Giả sử Parabol có dạng: 2
y = ax + bx + c , a ≠ 0 .
Chọn hệ trục Oxy như hình vẽ, khi đó parabol đi qua điểm A(100; 30) , và có đỉnh 30
=10000a +100b + c b − 1 C (0;5) . Suy ra: = 0 ⇒ ( P) 2 : y =
x + 5 . Đoạn AB chia 2a 400 5 = c
làm 8 phần, mỗi phần 25 m . Khi đó, tổng độ 1,0
dài của các dây cáp treo bằng OC + 2 y + 2 y + 2 y 1 2 3 1 1 1 2 2 2 = 5 + 2 .25 + 5 + 2 .50 + 5 + 2 .75 + 5 = 78,75(m) 400 400 400 2 2 2 2 2 2 4 4 2 2 2
a + b − c
a + c − b
(b − c ) − a (b − c ) VP = . a . c − . b = ... = 1,0 2ab 2ac 2bc a) 2 2 2 2 2
(b − c )(b + c − a ) 2 2 =
= (b − c ).cos . A 2bc 1,0
b) Gọi D là đi xác định bởi hệ thức: DB + DC − DA = 0. Ta có: 2 2 2 2 2 2 2 + − = + + − = Câu 3 MB MC MA MD DB DC DA 4,0 = 1,0
MD + DB + DC − (DB + DC)2 2 2 2 2
= ... = MD − 2AB.AC.cosA.
Nếu A tù, tập hợp các điểm M là tập ∅ . 1,0
Nếu A vuông, tập hợp các điểm M là { } D . .
Nếu A nhọn, tập hợp các điểm M là đường tròn ( ; D 2 A . B AC.cos A ) .
a) N ∈Ox sao cho AN nhỏ nhất khi N là hình chiếu của A lên Ox khi N là hình chiếu của 2.0
A lên Ox.Vậy N(3;0)
b) M ∈ d : y = x ⇒ M ( ; m m) Đường thẳng − − − =
AM có phương trình (m 1)x my 2m 0 m
AM cắt trục hoành tại 2 P( ; 0) 1,0 m −1
Câu 4 Đường thẳng MB có phương trình: (m − 2)x − (m +1) y + 3m = 0 4,0 m
MB cắt trục tung tại 3 Q(0; ) m +1 Phương trình m −1 m +1 PQ: x + y = 1(m ≠ 1 ± ;m ≠ 0) 2m 3m
PQ đi qua I (x ; y ) cố định ⇔ (3x + 2 y − 6)m − 3x + 2 y = 0 m ∀ ≠ 1 ± ;0 0 0 0 0 0 0 1,0 3x + 2y = 6 0 0 3 ⇔ ⇔ I(1; ) 3 − x + 2y = 0 2 0 0
Áp dụng BDDT Cauchy cho 6 số dương: 2 2 2
x , y , z , x, y, z ta được: 2 2 2 3 3 3 6 + + + + + ≥ = + + = x y z x y z 6 x y z 6 xyz. Vì 2 2 2 x y z 4 xyz nên ta có: 0,5
x + y + z ≥ 2 xyz. Dấu bằng xảy ra 2 2 2
⇔ x = y = z = x = y = z ⇒ x = y = z = 1 .
Câu 5 Trái với giả thiết: 2 2 2 + + = x y z 4 xyz . 0,5 1,0
Vậy x + y + z > 2 xyz.
Ghi chú: Học sinh làm theo các cách khác vẫn được chấm điểm theo từng bước có lời giải đúng.
Document Outline
- KIM LIÊN ĐE_DAP_AN_OLYMPIC K10_ 2018- 2019.pdf
- [TRUNGTRINH]THPT KIM LIÊN ĐE_DAP_AN_OLYMPIC K10_ 2018- 2019.pdf




