Đề thi Olympic Toán 10 năm 2023 – 2024 cụm Hà Đông & Hoài Đức – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
CỤM TRƯỜNG THPT HÀ ĐÔNG – HOÀI ĐỨC LỚP 10, LỚP 11
NĂM HỌC 2023 – 2024 Môn thi: TOÁN 10 ĐỀ CHÍNH THỨC Ngày thi: 28/3/2024
Thời gian làm bài: 150 phút
Câu 1 (6,0 điểm). 6  3 x
a) Tìm tập xác định của hàm số y  . 2 x  4x  3
b) Tìm tất cả các giá trị của tham số m 2
để đồ thị P : y  x  3x  m cắt đường thẳng 2
y  2x  2 tại hai điểm phân biệt có hoành độ x ,x thỏa mãn x  x 8x x 1. 1 2    1 2 1 2
c) Cho bất phương trình 3  x  6  x  3  x 6  x   m. Tìm tất cả các giá trị của tham
số m để bất phương trình nghiệm đúng với mọi   x    3;  6 .
Câu 2 (4,0 điểm). 3 b  3 c  3 a
a) Cho tam giác ABC có AB  , c AC  ,
b BC  a thỏa mãn  2 a . Tính góc
b  c  a  BAC.
b) Cho tam giác ABC đều cạnh a và M là điểm di động trên đường thẳng AB. Tìm giá trị nhỏ   
nhất của biểu thức T  2MA  MB  MC .
Câu 3 (4,0 điểm).
a) Giải phương trình 2
x  x  4  2 x  11  x  .
b) Nhà máy dự định dùng hai loại nguyên liệu để sản xuất ít nhất 140 kg chất A và 18 kg chất B.
Với mỗi tấn nguyên liệu loại I, nhà máy chiết xuất được 20 kg chất A và 1, 2 kg chất B. Với mỗi
tấn nguyên liệu loại II, nhà máy chiết xuất được 10 kg chất A và 3 kg chất B. Giá mỗi tấn nguyên
liệu loại I là 8 triệu đồng và loại II là 6 triệu đồng. Hỏi nhà máy phải dùng bao nhiêu tấn nguyên
liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đạt mục tiêu đề ra. Biết rằng cơ sở cung
cấp nguyên liệu chỉ có thể cung cấp tối đa 9 tấn nguyên liệu loại I và 8 tấn nguyên liệu loại II.
Câu 4 (2,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân tại A có phương trình
đường thẳng chứa cạnh AB là x  2y  2  0 , phương trình đường thẳng chứa cạnh AC là  
2x  y  1  0, biết điểm M 1;2 thuộc đoạn thẳng BC. Tìm tọa độ điểm D sao cho DB.DC có giá trị nhỏ nhất. Câu 5 (4,0 điểm).
a) Cho tam giác ABC có ba cạnh AB  ,
c BC  a,AC  ;
b độ dài các đường cao hạ từ đỉnh ;
A B;C lần lượt là h ;h ;h thỏa mãn a sin A  b sin B  c sinC  h  h  h . Chứng minh tam giác a b c a b c
ABC là tam giác đều.
b) Xét các số thực x,y,z thỏa mãn đồng thời 0  x  y  z  1 và 3x  2y  z  4, tìm giá trị lớn
nhất của biểu thức S  2 x  2 y  2 3 2 z .
…………. HẾT…………
Họ và tên thí sinh…………………………………………………; Số báo danh……………………………………….
Chữ ký cán bộ coi thi số 1:………………………………..Chữ ký cán bộ coi thi số 2:……………………………….
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
CỤM TRƯỜNG THPT HÀ ĐÔNG – HOÀI ĐỨC LỚP 10, LỚP 11
NĂM HỌC 2023 – 2024 Môn thi: TOÁN 10 Ngày thi: 28/3/2024 HƯỚNG DẪN CHẤM Câu Nội dung Điểm 1a 6  3 x (2 điểm)
Tìm tập xác định của hàm số y  . 2 x  4x  3 6  3 x   0 Điều kiện:  2
x  4x  3  0, 5  0  x   2 2  x  2        2  x  2    x      1    x  1     .  1,0   x  1   x         x  3  3     Tập xác định   D  2;2 \      1 . 0,5 1b
Tìm tất cả các giá trị của tham số m 2
để đồ thị P : y  x  3x  m cắt đường thẳng … (2 điểm)
Phương trình hoành độ giao điểm 2
x  3x  m  2x  2  2
x  5x  m  2  0   1 0,5 Ta có   2 5  4m  
2  33  4m . Phương trình (1) có hai nghiệm phân biệt x ;x 1 2 33 0,5
khi và chỉ khi   0  33  4m  0  m  . 4
x  x    5
Áp dụng định lí Vi ét cho phương trình (1) ta có  1 2 
x .x  m   2 1 2 2
Theo đề ra ta có x  x 8x x 1 0,5 1 2    1 2  2 x  2x x  2
x  8x x  1  x x 4x x 1 1 1 2 2 1 2   1 2 2   1 2 2
 5  4m  2  1  17  4m  1  m  4.(Thỏa mãn điều kiện). 0,5 1c
Tìm tất cả các giá trị của tham số m để bất phương trình (2 điểm)
3  x  6  x  3  x6  x  m  
nghiệm đúng với mọi x    3;  6 Đặt 2
t  3  x  6  x  t  9  2 3  x 6  x   9. (1)   0,5
Ta có: 1. 3  x  1. 6  x 
3 x6 x 1        1 t 3 2. (2)
Từ (1) và (2), suy ra 3  t  3 2. 2 t 9 Khi đó: 2
t  9  2 3  x 6  x 
3 x6 x      . 2  0, 5 Bất phương trình thành: 2 t
  2t  9  2m , t    3; 3 2     . Xét f t 2  t
  2t  9 có đồ thị là parabol có đỉnh I 1;1 
0 . Lập bảng biến thiên trên  0,5 3; 3 2    Max f t  6 t      khi 3 . 3;3 2    
Vậy yêu cầu bài toán  2m  6  m  3. 0,5 2a 3 b  3 c  3 a 2 (2điểm)
Cho tam giác ABC có AB  , c AC  ,
b BC  a thỏa mãn
 a . Tính góc
b  c a  BAC. 3 b  3 c  3 a Ta có  2 a  3 b  3 c  2 a b  2 a c 0,5
b  c a  2   2  2  2  2  2 b bc c a b c a  bc 0,5 2 b  2 c  2 a 1   cos A    A  6  0 . 1,0 2bc 2 2b
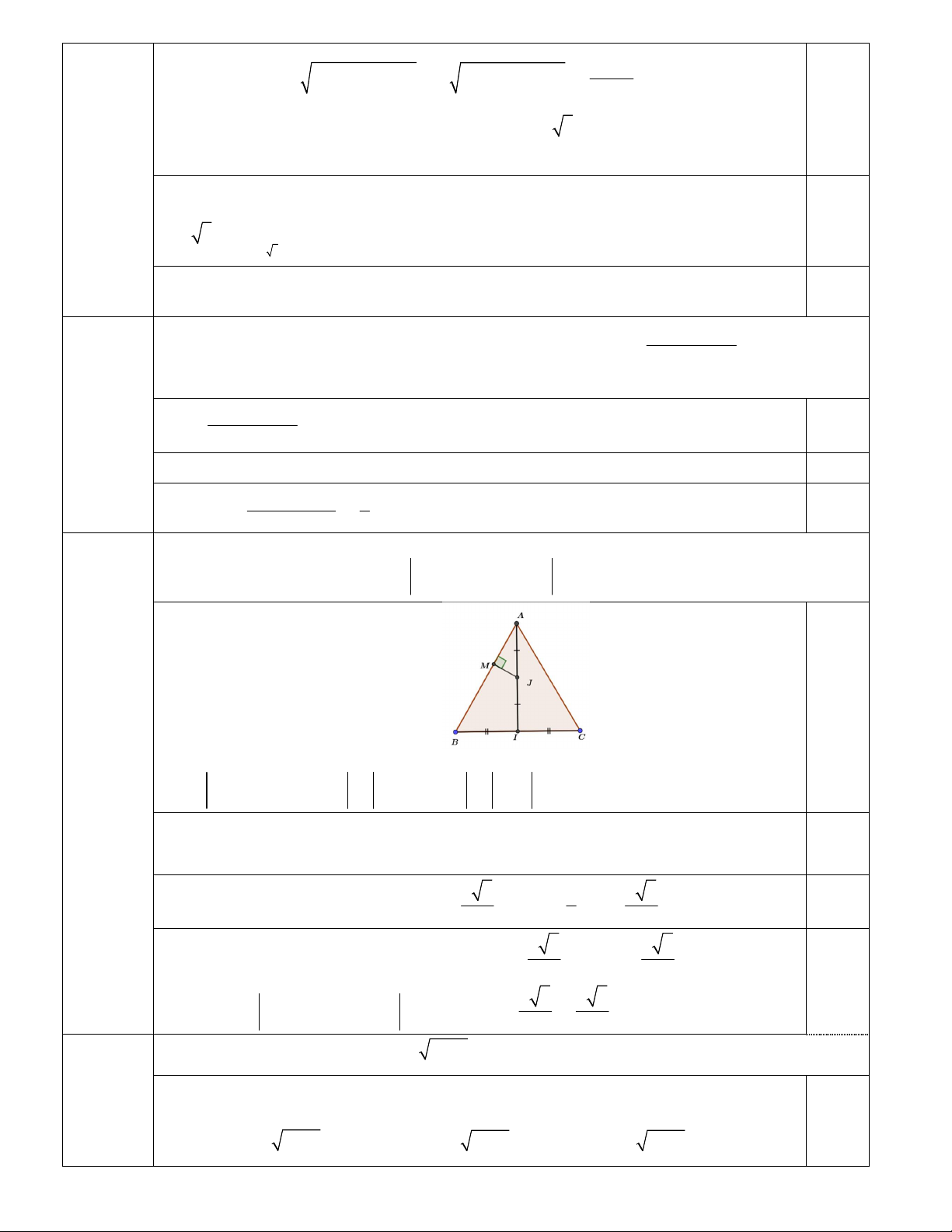
Cho tam giác ABC đều cạnh a và M là điểm di động trên đường thẳng AB . Tìm giá trị nhỏ    (2 điểm)
nhất của biểu thức T  2MA  MB  MC . 0,5
Gọi I là trung điểm BC và gọi J là trung điểm AI .      
Ta có 2MA  MB  MC  2MA  2MI  4MJ  4MJ
Do M là điểm di động trên đường thẳng AB nên để MJ min  M 0,5
là hình chiếu vuông góc của J lên đường thẳng AB. a 3 1 a 3
Vì tam giác ABC đều có cạnh a  AI 
 JA  AI  . 0,5 2 2 4  a 3 a 3
Xét JAM vuông ở M có: JM  J . A sin MAJ  .sin 30  . 4 8    0,5 a 3 a 3
 2MA  MB  MC  4MJ  4.  . min 8 2 3a
Giải phương trình: 2
x  x  4  2 x  1 1  x. (2 điểm)
Điều kiện: x  1 *. Ta có: 0,5 2
x  x  4  2 x  1 1  x  2
 x  2x x  1  x  1  2x  x 1 3  0
 x  x  2
1  2x  x 1 3  0
Đặt x  x  1  y (Điều kiện: y  1 * 
* ), phương trình trở thành: y   1 0,5 2
y  2y  3  0  y   1 y  3  0   y   3 
Với y  1 (không thỏa mãn điều kiện *  * )
Với y  3 (thỏa mãn điều kiện *  * ), ta có phương trình: 0,5 1   x  3 1   x  3
x  x  1  3  
 x  1  3  x      2 x
  1  9  6x  x 2       x 7x 10 0  1   x  3    x  2 
 x  2 (thỏa mãn điều kiện *)  0,5  x   5  
Vậy phương trình có nghiệm x  2. 3b
Nhà máy dự định dùng hai loại nguyên liệu để sản xuất ít nhất 140 kg chất A và 18 kg chất (2 điểm) B…
Gọi x,y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng
Điều kiện: 0  x  9; 0  y  8
 Khối lượng chất A được chiết xuất từ
 Nguyên liệu loại I là 0, 020x (tấn) 0,5
 Nguyên liệu loại II là 0, 010y (tấn)
Theo giả thiết, ta có bất phương trình 0, 02x  0, 01y  0,14 hay 2x  y  14
 Khối lượng chất B được chiết xuất từ
 Nguyên liệu loại I là 0, 0012x (tấn)
 Nguyên liệu loại II là 0, 003y (tấn)
Theo giả thiết, ta có bất phương trình 0, 0012x  0, 003y  0, 018 hay
2x  5y  30
Khi đó để chi phí mua nguyên liệu là ít nhất mà vẫn đạt mục tiêu đề ra thì ta cần
tìm x,y sao cho biểu thức F x,y  8x  6y nhỏ nhất với x,y thỏa mãn hệ 0,5 0  x   9 0  y   8 bất phương trình  2x  y   14
2x  5y   30
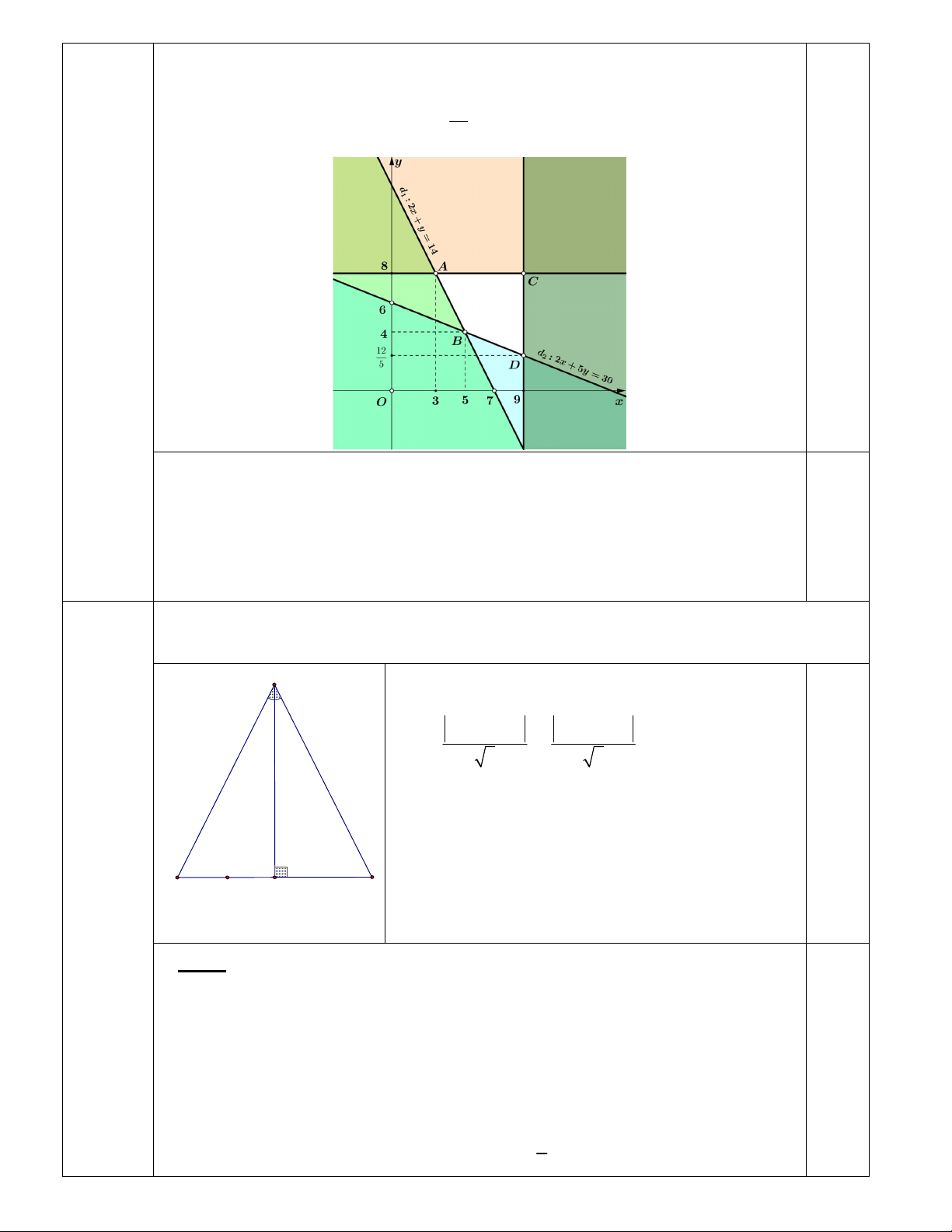
Biểu diễn miền nghiệm của hệ bất phương trình trên, ta được miền ngiệm của
hệ là miền trong tứ giác ABCD (như hình vẽ), với
A8;3,B 5;4,C 9;8    12 ,D 9;     5    0,5
 Tại đỉnh B, ta có F  64
 Tại đỉnh C , ta có F  120  Tại đỉnh ,
D ta có F  86, 4 0,5
Vậy cơ sở cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II thì chi
phí thấp nhất 64 triệu đồng. 4
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân tại A có phương trình (2 điểm)
đường thẳng chứa cạnh AB là: x  2y  2  0 , …
+) Các đường phân giác góc A là tập hợp các điểm A
cách đều AB, AC nên có phương trình: x  2y  2 2x  y  1
x  y  3  0    
3x  3y  1   0 5 5
+) Do ΔABC cân tại A nên phân giác trong (l ) a 0,5 l
của góc A vuông góc với BC. B M C 
+) TH1: (l ) : x  y  3  0 , khi đó BC đi qua M(1;2)và có vtpt n  (1;1) ; a 1
 Phương trình BC :x  y  3  0  
x  2y  2  0 x    4
Tọa độ B là nghiệm hệ PT:     B(4;1) 
x  y  3  0 y     1 0,5  
2x  y  1  0 x     4
Tọa độ C là nghiệm hệ PT:     C  ( 4;7) 
x  y  3  0 y    7     3
Khi đó MB  3; 
3 ; MC  5;5  MB   MC  B,C nằm về hai phía (l ) 5 a ( thỏa mãn) 
+) TH2: (l ) : 3x  3y  1  0 , khi đó BC đi qua M(1;2) và có vtpt n  (1;1) a 2
 Phương trình BC : x  y  1  0  
x  2y  2  0 x    0
Tọa độ B là nghiệm hệ PT:     B(0;1) 
x  y  1  0 y    1  2
2x  y  1  0 x     2 1 0,5
Tọa độ C là nghiệm hệ PT:    3  C  ( ; ) 
x  y  1  0    1 3 3 y   3      5 5
Khi đó MB  1;  1 ; MC    ;     cùng hướng (loại). 3 3    
Với B(4;1);C 4;7. Gọi D x;y  DB  4  x;1  y, DC  4  x;7  y    2 x  0  DB DC  2 x  2 y  y   2 . 6 23
x  y   3  32  32  . Dấu '  '   0,5 y   3  
Vậy D(0; 3) thì D .
B DC nhỏ nhất bằng 32. 5a
Cho tam giác ABC có ba cạnh AB  ,
c BC  a,AC  ;
b độ dài các đường cao hạ từ đỉnh ( 2 điểm) ;
A B;C lần lượt là h ;h ;h thỏa mãn… a b c Ta có: 2 2 2 a b c 2S 2S 2S 1 1 1 1      
 2a  2b  2c      4S       0,5 2R 2R 2R a b c R a b c      1 1 1 2 2 2  
 a  b  c  abc      2 a  2 b  2
c  ab  bc    ca  . a b c    0,5 Do: , a ,
b c  0 nên áp dụng BĐT Cô Si, ta có:  2 a  2 b   2ab  0,5  2 b  2 c  2bc  2 a  2 b  2
c  ab  bc  ca   2 c  2 a   2ca
Đẳng thức xảy ra khi tam giác ABC là tam giác đều. 0,5 5b
Xét các số thực x,y,z thỏa mãn đồng thời 0  x  y  z  1 và 3x  2y  z  4, tìm giá trị lớn (2 điểm)
nhất của biểu thức S  2 x  2 y  2 3 2 z . 2
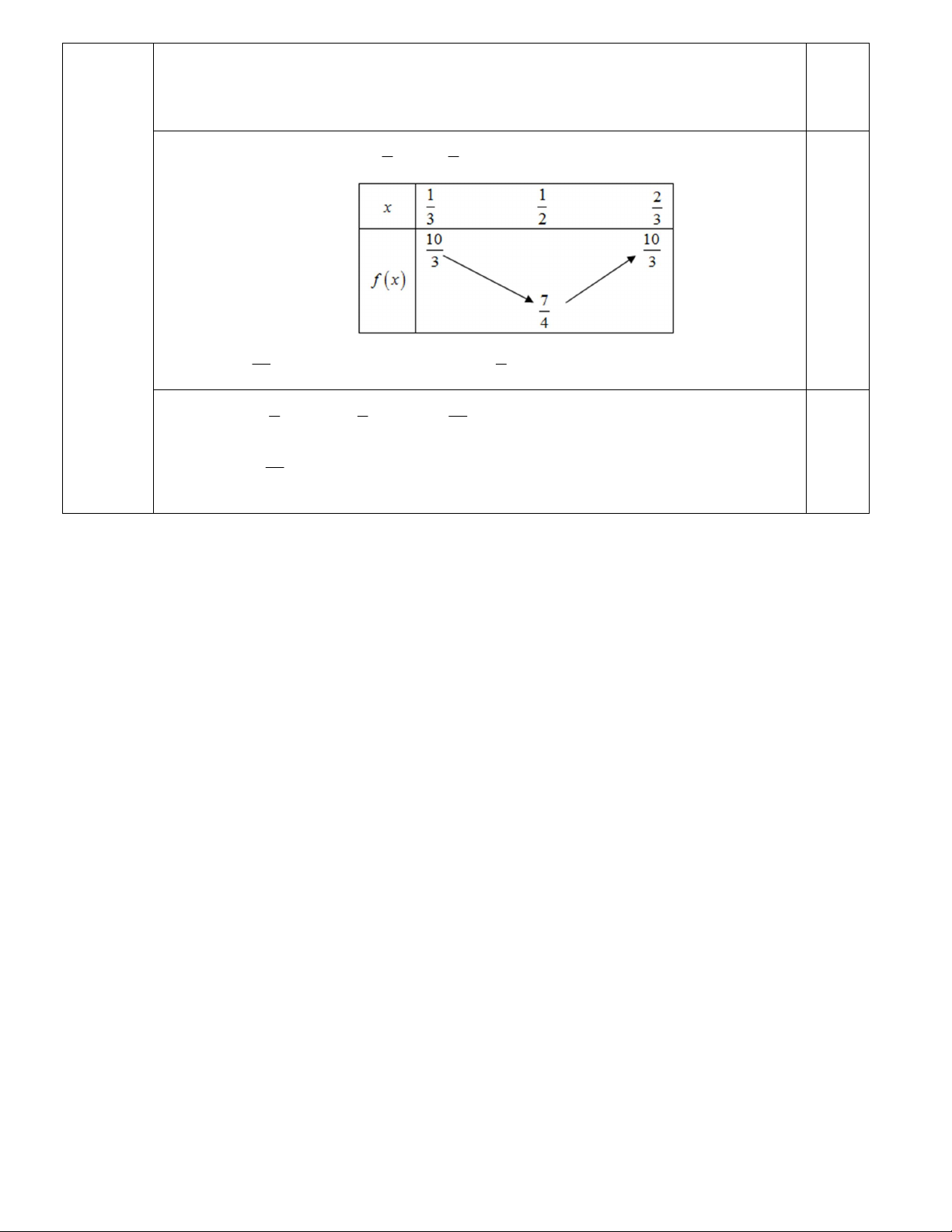
Ta có: 4  3x  2y  z  6x  0  x  . 3 0,5 1 2 TH1:  x  . 3 3 0,5  2 y   y
Vì 0  y  z  1   2 2 S 3x 2y z 3x 3x 4         . 2 z   z 1 2
Đặt f x   2
3x  3x  4 với  x  . Lập bảng biến thiên: 3 3 0,5 10 1 Suy ra: S 
. Dấu đẳng thức xảy ra  x 
; y  z  1 . 3 3 1 1 10 TH2: 0  x 
 S  3.  1  1  . 3 9 3 0,5 10 Vậy max S  . 3
Các cách giải khác đáp án nếu đúng vẫn cho điểm tối đa tương ứng.