Đề thi Olympic Toán 10 năm học 2019 – 2020 cụm Sóc Sơn – Mê Linh – Hà Nội

SỞ GD&ĐT HÀ NỘI
KỲ THI OLYMPIC LỚP 10 CÁC TRƯỜNG THPT NĂM HỌC 2019-2020
CỤM SÓC SƠN - MÊ LINH Môn thi: TOÁN
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1. (4,0 điểm)
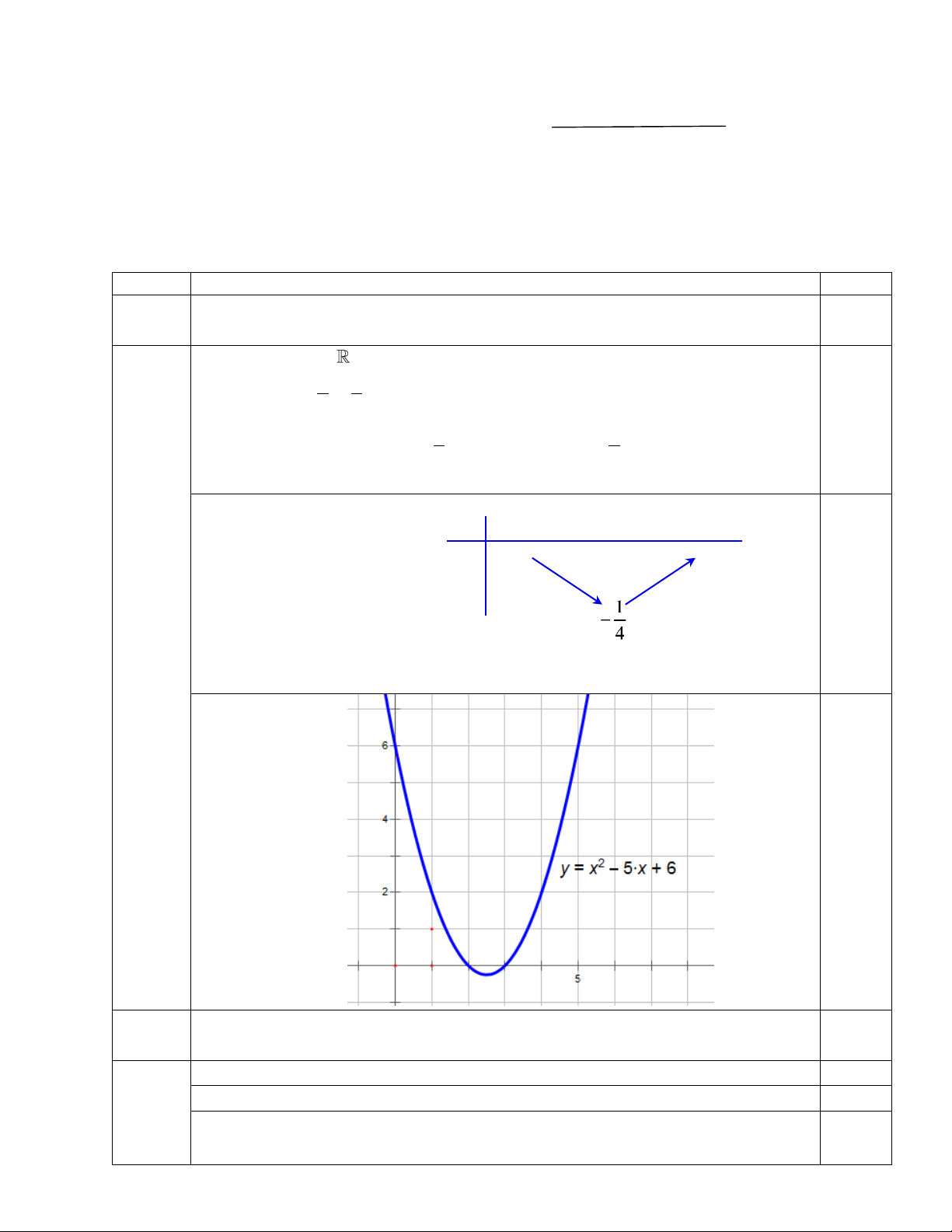
1. Lập bảng biến thiên và vẽ đồ thị hàm số 2
y  x  5x  6 .
2. Tìm m để đường thẳng y  x  m1cắt đồ thị hàm số 2
y  x  4x  6 tại hai điểm phân biệt.
Câu 2. (6,0 điểm)
1. Giải bất phương trình 3 2
14  3x  x  7  x 1 2 4 2
x  y  xy  2xy 7
2. Giải hệ phương trình  3 2 2
xy  x y  4xy 11x  2811y
3. Một người có một khu đất bãi rộng dọc theo bờ sông. Người
Con sông
đó muốn làm một hàng rào hình chữa E (như hình vẽ) để được
khu đất hình chữ nhật gồm hai phần để trồng rau và chăn nuôi.
Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên
vật liệu là 80000 đồng một mét dài, đối với phần còn lại thì chi
phí nguyên vật liệu là 40000 đồng một mét dài. Tính diện tích
lớn nhất của phần đất mà người đó rào được với chi phí vật liệu 20 triệu đồng.
Câu 3. (4,0 điểm)
Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD vuông tại A và D2;2 , cạnh CD  2AB .
Gọi H là hình chiếu của D lên cạnh AC và M là trung điểm HC. Biết phương trình đường thẳng DH
và BM lần lượt là 2x  y 6  0 và 4x  7y 61 0. Tìm tọa độ các đỉnh A, B, C của hình thang.
Câu 4. (3,0 điểm)
Cho tam giác ABC. O là điểm tùy ý trong tam giác. Gọi M, N, P lần lượt là hình chiếu của O lên BC AC AB 2 p
cạnh BC, AC, AB. Chứng minh rằng   
, trong đó p là nửa chu vi và r là bán OM ON OP r
kính đường tròn nội tiếp tam giác ABC.
Câu 5. (3,0 điểm)
Cho các số thực dương a, b, c. Tìm giá trị nhỏ nhất của biểu thức 2 2 2 a b c P    3  b  c 3  bc ca 3 2 2  ca a b2 5 5  5ab --- Hết --- SỞ GD&ĐT HÀ NỘI
KỲ THI OLYMPIC LỚP 10
CÁC TRƯỜNG THPT CỤM NĂM HỌC 2019-2020 SÓC SƠN - MÊ LINH Môn thi: TOÁN
Thời gian: 150 phút (không kể thời gian giao đề) HƯỚNG DẪN CHẤM Bài Nội dung Điểm Bài I.1
Lập bảng biến thiên và vẽ đồ thị hàm số 2
y  x  5x  6 . 2.0
Tập xác định D  0.5  5 1  Tọa độ đỉnh I ;     2 4   5   5 
Hàm số nghịch biến trên  ;    và đồng biến trên ;      2   2  Bảng biến thiên 0.5 x – ∞ 5/2 + ∞ + ∞ + ∞ y 1.0 Vẽ đồ thị Bài I.2
Tìm m để đường thẳng y  x  m 1 cắt đồ thị hàm số 2
y  x  4x  6 tại hai điểm 2.0 phân biệt.
Xét phương trình hoành độ giao điểm 2
x  4x  6  x  m 1 0.5 2
 x  5x  6  m 1 0.5
Phương trình có hai nghiệm phân biệt khi và chỉ khi đường thẳng y  m 1 cắt đồ 0.5 thị hàm số 2
y  x  5x  6 tại hai điểm phân biệt. 0.5 Khi đó 1 3 m 1    m  4 4
Bài II.1 Giải bất phương trình 3 2
14  3x  x  7  x 1 2.0 Điều kiện: x 1 0.5
BPT   3 14 3x  2   2
x  4   x 1   1  0 32  x x  2 0.5    2 x  4   0 3   x2 3 x 1 1 14 3  2 14  3x  4   0.5 3  1 x 2 x 2        0  *     3   x2 3 x 1 1 14 3  2 14  3x  4  
Vì biểu thức trong ngoặc vuông bằng 0.5 3 14  3x2 3  2 14  3x 1 1  x 1  0 x  1 3   x2 3 x 1 1 14 3  2 14  3x  4 nên  
*  x  2 (thỏa mãn điều kiện). Vậy tập nghiệm là S  2;  Bài II.2 2 4 2
x  y  xy  2xy  7 2.0
Giải hệ phương trình  * 3 2 2
xy  x y  4xy 11x  2811y  0.5 x  y  2 2  xy  7 Hệ   *   xy   2
y  x 11 2
x  y   4xy  28 Đặt 2 u  y  ; x v  xy 0.5 2 2    v   7 7  u u v      u
 v  4v 11u  28 u   2 7  u   4 2
7  u  11u  28 u   0,v  7 0.5 3 2
 u  4u  4u  0   u   2  ;v  3 - Với 3 3
u  0, v  7  x  49; y  7 0.5
- Với u  2, v  3  x  3; y  1 . Vậy tập nghiệm là    3 3 3;1 ; 49; 7 
Bài II.3 Một người có một khu đất bãi rộng dọc theo bờ sông. Người đó muốn làm một 2.0
hàng rào hình chữa E (như hình vẽ) để được khu đất hình chữ nhật gồm hai phần
để trồng rau và chăn nuôi. Đối với mặt hàng rào song song với bờ sông thì chi phí
nguyên vật liệu là 80000 đồng một mét dài, đối với phần còn lại thì chi phí
nguyên vật liệu là 40000 đồng một mét dài. Tính diện tích lớn nhất của phần đất
mà người đó rào được với chi phí vật liệu 20 triệu đồng.
Con sông
Gọi x (m) là chiều dài hàng rào vuông góc với bờ sông, y (m) là chiều dài hàng 0.5
rào song song với bờ sông . Theo giả thiết thì 3 .4 x 0000  .8
y 0000  20000000  x  0, y  0 500  3x  0.5
3x  2 y  500  y  2 3 500 0.5
Diện tích khu vườn sau khi rào là 2 S  xy   x  250x, 0  x  2 3 3  500  0.5
Xét tam thức f  x 2
  x  250x trên 0; 
 , suy ra diện tích lớn nhất là 2  3  31250  250 2 m  khi x  (m) 3 3 Bài III
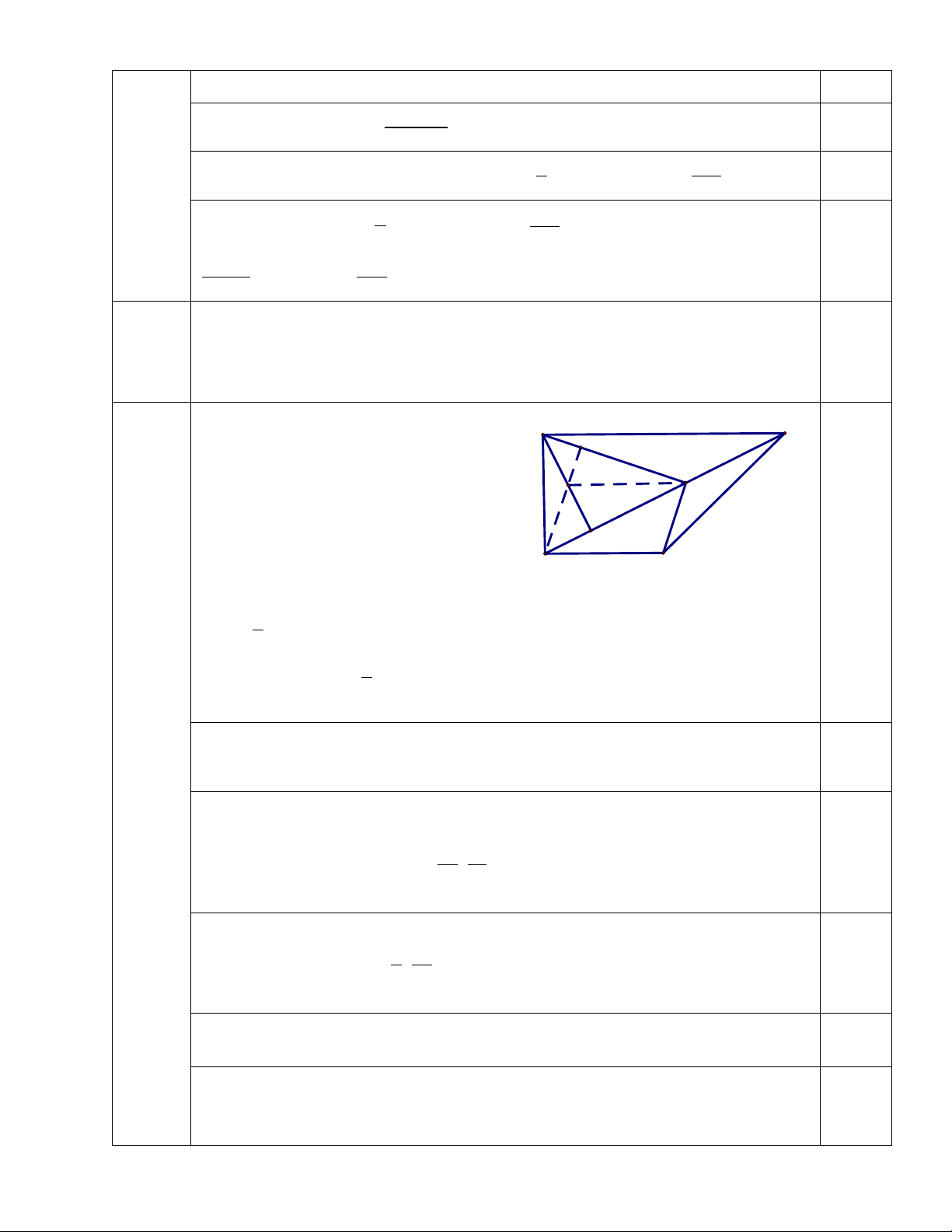
Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD vuông tại A và D 2; 2 , cạnh 4.0
CD  2AB . Gọi H là hình chiếu của D lên cạnh AC và M là trung điểm HC. Biết
phương trình đường thẳng DH và BM lần lượt là 2x  y  6  0 và 4x  7 y  61  0
. Tìm tọa độ các đỉnh A, B, C của hình thang. D (2;2) C K M H 4x+7y-61=0 A B
- Gọi K là trung điểm DH  KM là đường trung bình trong tam giác CDH và 1 KM  DC . 2 1
Mà AB / / DC; AB 
DC  Tứ giác ABMK là hình bình hành. 0.5 2
- Vì AB  AD, KM / / AB nên KM  AD , do đó K là trực tâm tam giác ADM 0.5
 AK  DM  BM  DM
- Khi đó đường thẳng DM qua D và vuông góc BM có phương trình là 0.5
7x  4 y  6  0 .  22 31
- Ta có M  DM  BM  M ;    5 5 
- Đường thẳng AC qua M và vuông góc DH có phương trình là x  2 y  8  0 . Ta 0.5  4 22 
có H  AC  DH  H ;   .  5 5 
Vì M là trung điểm CH nên C 8;8 . 0.5
- Đường thẳng AD qua D và vuông góc CD có phương trình là x  y  4  0 . Ta 0.5
có A  AD  AC  A0; 4 . 1 0.5 - Vì AB 
DC  B 3;7 . 2
Vậy A0;4, B 3;7, C 8;8 0.5 Bài IV
Cho tam giác ABC. O là điểm tùy ý trong tam giác. Gọi M, N, P lần lượt là hình 3.0 BC AC AB 2 p
chiếu của O lên cạnh BC, AC, AB. Chứng minh rằng    , trong OM ON OP r
đó p là nửa chu vi và r là bán kính đường tròn nội tiếp tam giác ABC. 0.5 - Có         2 2 2 2 2 BC AC AB BC AC AB 2  0.5 BC AC AB  =  . BC.OM  . AC.ON  . A . B OP    OM ON OP    BC AC AB  0.5     B . C OM  A . C ON  A . B OP  OM ON OP   BC AC AB  0.5 2  4 p    .2S   ABC   OM ON OP  - Vì S
 pr nên suy ra điều phải chứng minh. 0.5 ABC  BC AC AB 0.5
- Dấu = xảy ra khi và chỉ khi OM ON OP  
 OM  ON  OP BC.OM AC.ON A . B OP
 O là tâm đường tròn nội tiếp tam giác ABC. Bài V
Cho các số thực dương a, b, c. Tìm giá trị nhỏ nhất của biểu thức 3.0 2 2 2 a b c P    3  b  c 3  bc c  a 3 2 2  ca a b2 5 5  5ab 2
Ta có b  c   2 2 2 b  c  . 0.5 2
Suy ra b  c  bc   2 2 5
2 b  c   5bc  b  2cc  2b 2 2 0.5 Do đó a a  
b  c2  5bc
b  2cc  2b b  2c c  2b
b  2c c  2b 0.5 Mặt khác 3
a  b  c  a    3 . a . 3 3 3 3 2 a a 2 a a 0.5 3  3 3     3 3.
b  cc  b 3. 2 2
a  b  c
bc2 5bc
a  b  c 2 2 0.5 Tương tự b b c c có 3  3  3  ; 3 3. 2 c  a 3. 2  5ca
a  b  c
a b 5ab
a  b  c Do vậy 3
P  3 . Dấu = xảy ra khi a  b  c . Vậy 3 min P  3 0.5
* Lưu ý: Học sinh có thể làm theo cách khác, nếu đúng vẫn cho điểm theo thang điểm của câu.
Document Outline

• De Olympic TOAN 10
• TOAN 10_Dapan