PHÒNG GIÁO DỤC VÀ ĐÀO TẠO TỨ KỲ
ĐỀ THI OLYMPIC CẤP HUYỆN
HỘI ĐỒNG THI OLYMPIC NĂM HỌC 2022 - 2023 MÔN: TOÁN - LỚP 7
Thời gian làm bài: 120 phút
(Đề thi gồm 05 cầu, 01 trang)
Câu 1. (2,0 điểm)
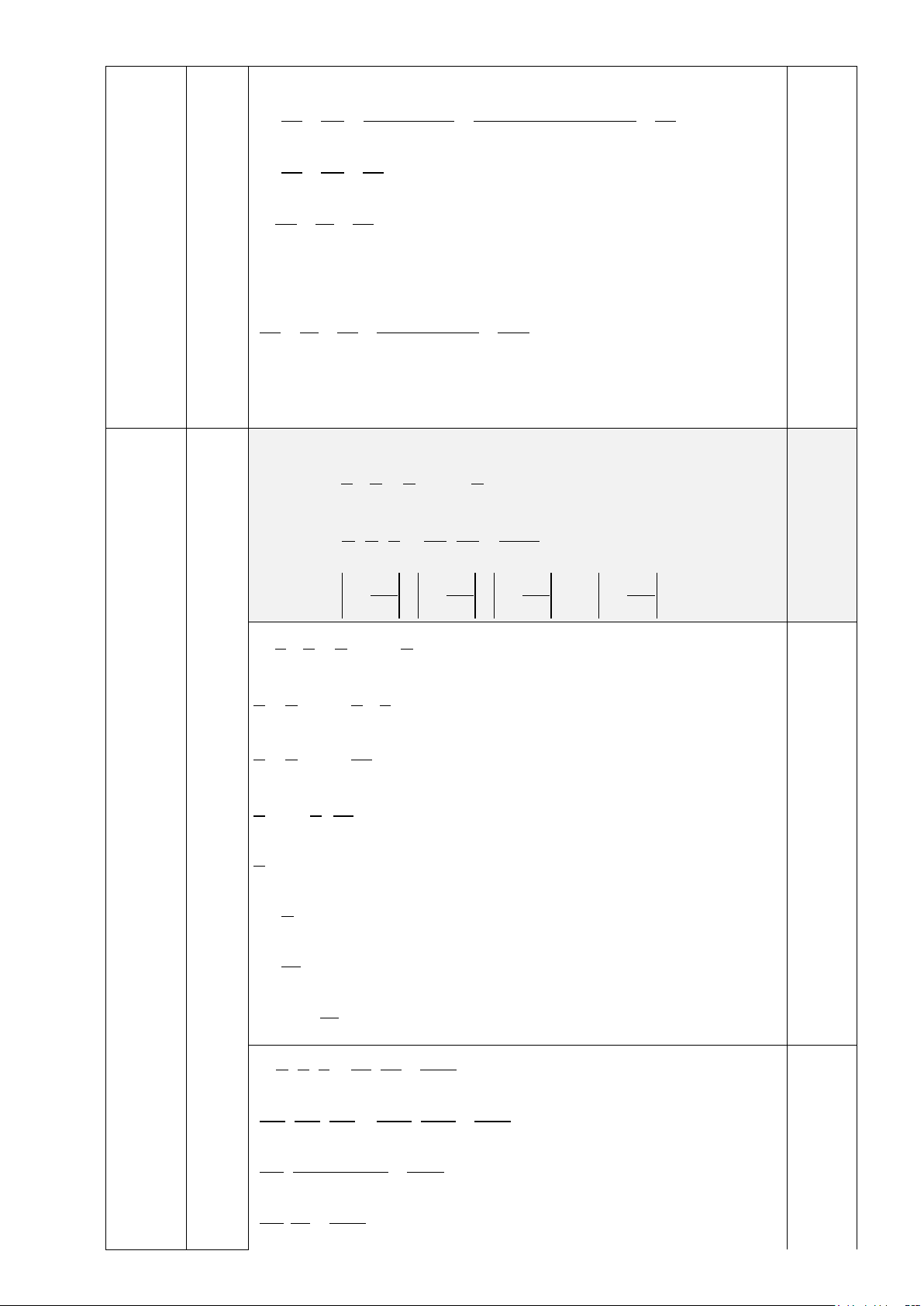
1) Thực hiện phép tính a)  2 3  191 33  7 11  1011 9 −  . +  : +  .  +   191 382 17 34  1011 2022 25 2      0 b) 2 1 25  2023 11 72 1 :  − − − 2 4  2024    c)  1  1  1   1  1 1 1 1.... 1 1 − − − − −  2 2 2 2 2 2 3 4 99 100        
2) Tính giá trị biểu thức A = (x − y + z + )2023 2 25
biết: 3x = 4y = 5z − 3x − 4y và 2x + y = z −19
Câu 2. (2,0 điểm)
1) Tìm x, biết a) 3 2  2  1 1 2 3 14 15 1 + : −  x = b) ⋅ ⋅ ⋅⋅⋅ ⋅ = 5 5 3    2 2 1 4 6 8 30 32 2 x+ c) 1 2 3 100 x + + x + + x + + ...+ x + =102x 101 101 101 101
2) Cho 3 số thực x, y,z thỏa mãn: x y z = = . 2021 2022 2023
Chứng minh: (x − z)3 = (x − y)2 8 ( y − z)
Câu 3. (2,0 điểm)
a) Cho a,b là các số nguyên dương, chứng minh rằng biểu thức ab( 2 a + )( 2 2 b + 2) luôn chia hết cho 9.
b) Tìm cặp số tự nhiên ( ;x y) trong đó y là chữ số, biết rằng: 1+ 2 +...+ (x − ) 1 = yyy − x
Câu 4. (3,0 điểm)
Cho tam giác ABC cân tại A ( AB > BC ). Gọi F là trung điểm của AC , qua F kẻ đường
thẳng vuông góc với AC cắt đường thẳng BC tại M . Trên tia đối của tia AM lấy điểm N sao cho AN = BM . a) Chứng minh:  =  AMC BAC .
b) Chứng minh: AM = CN
c) Lấy điểm D trên cạnh AC , điểm E trên cạnh AB sao cho AD = AE . Trên tia BM
lấy I sao cho BI = DE . Chứng minh: 𝐸𝐸𝐸𝐸 // 𝐷𝐷𝐷𝐷 và BC DE BD + > . 2
Câu 5. (1,0 điểm)
Cho các số nguyên dương ; a ;
b c thỏa mãn a + b + c = 2023. Chứng minh rằng giá trị biểu
thức sau không phải là một số nguyên: a b c A = + +
2023− c 2023− a 2023− b
---------- Hết ---------
(Chú ý: Học sinh không được sử dụng máy tính cầm tay khi làm bài.) HƯỚNG DẪN CHẤM ĐỀ THI OLYMPIC NĂM HỌC 2022 -2023
Môn: Toán – Lớp 7 Câu ý Nội dung Điểm
1) Thực hiện phép tính a)  2 3  191 33  7 11  1011 9 −  . +  : +  .  +   191 382 17 34  1011 2022 25 2      0 b) 2 1 25  2023 11 72 1 :  − − − 2 4  2024    c)  1  1  1   1  1 1 1 1.... 1 1 − − − − −  2 2 2 2 2 2 3 4 99 100         a)  2 3  191 33  7 11  1011 9 −  . +  : +  .  +   191 382 17 34  1011 2022 25 2       4 3  191 33  14 11  1011 9 = −  . +  : +  .  +  0,25  382 382 17 34  2022 2022 25 2       1 191 33  25 1011 9 . : .  = + +  382 17 34 2022 25 2      1 33 1 9 = + : +  34 34   2 2  0,25 1 =1:5 = 5 0 b) 2 1 25  2023 11 72 1 :  − − −   2 4  2024  0,25 Câu 1 3 5 = 121− 72 − : −1 3 2 = 49 − . −1 2,0 1) 2 2 2 5 3 3 điểm = 7 − −1 = 6 − 27 = 0,25 5 5 5 c)  1  1  1   1  1 1 1 1.... 1 1 − − − − −  2 2 2 2 2 2 3 4 100 101        
Do tích có 100 thừa số âm nên tích mang dấu dương.  1  1  1   1  1 0,25 1 1 1.... 1 1 − − − − −  2 2 2 2 2 2 3 4 100 101         1.3 2.4 3.5 100.102 = ⋅ ⋅ ⋅ 2 2 2 2 2 3 4 101 1.3.2.4....100.102 = 2 2 2 2 2 .3 .4 ....101 1.2.3.4....100 3.4.5...102 = . 1 102 = . 51 = . 0,25 2.3.4....101 2.3.4...101 101 2 101
2) Tìm x, y, z biết: 3x = 4y = 5z −3x−4y và 2x+ y = z −19
Ta có: 3x = 4y = 5z −3x − 4y
3x 4y 5z − 3x − 4y 3x + 4y + 5z − 3x − 4y 5z ⇒ = = = = 1 1 1 1+1+1 3 3x 4y 5z 0,25 ⇒ = = 1 1 3 x y z ⇒ = = 20 15 36
Lại có: 2x + y = z −19 ⇒ 2x + y − z = 19 −
Áp dụng tính chất dãy tỉ số bằng nhau ta có: x y z
2x + y − z 19 − = = = = = 1 − 20 15 36 2.20 +15 − 36 19 0,25 Suy ra: x = 20 − ; y = 15 − ; z = 36 −
Vậy A = (− + − + )2023 20 30 36 25 = 1 −
1) Tìm x, biết   a) 3 2 2 1 + : −  x = 5 5 3    2 1 2 3 14 15 1 b) ⋅ ⋅ ⋅⋅⋅ ⋅ = 2 1 4 6 8 30 32 2 x+ c) 1 2 3 100 x + + x + + x + + ...+ x + =102x 101 101 101 101   Câu 2 a) 3 2 2 1 + : −  x = 5 5 3    2 2,0 2  2  1 3 điểm : −  x = − 0,25 5 3    2 5 2  2  1 : −  x − = 5 3    10 2 2 1 x : − − = 1) 3 5 10 2 − x = 4 − 3 2 x = + 4 0,25 314 x = 3 Vậy 14 x = 3 b) 1 2 3 14 15 1 ⋅ ⋅ ⋅⋅⋅ ⋅ = 2 1 4 6 8 30 32 2 x+ 1 2 3 14 15 1 ⋅ ⋅ ⋅⋅⋅ ⋅ = 2 1
2.2 2.3 2.4 2.15 2.16 2 x+ 0,25 1 1.2.3...14.15 1 ⋅ = 15 2 1 2 2.3.4...15.16 2 x+ 1 1 1 . = 15 2 1 2 16 2 x+ 1 1 = 19 2 1 2 2 x+ 2x +1 =19 2x =18 0,25 x = 9 Vậy x = 9 c) 1 2 3 100 x + + x + + x + + ...+ x + =102x 101 101 101 101
Điều kiện: 102x ≥ 0 ⇒ x ≥ 0 0,25 Với x ≥ 0 ta có: 1 2 3 100 x + + x + + x + + ...+ x + = 102x 101 101 101 101 ⇔ ( x − x) 1 100.101 100 102 + . = 0 101 2 ⇔ 2 − x + 50 = 0 ⇔ 2 − x = 50 − 0,25 ⇔ x = 25 (TMĐK) Vậy x = 25
Cho 3 số thực x, y,z thỏa mãn: x y z = = . 2021 2022 2023
Chứng minh rằng: (x − z)3 = (x − y)2 8 ( y − z) Ta có: x y z = = 2021 2022 2023 x − z x − y y − z ⇒ = = 0,25
2021− 2023 2021− 2022 2022 − 2023
x − z x − y y − z 2) ⇒ = = 2 − 1 − 1 − 3 2  x − z   x − y  ⇒ =     . y − z  2 −   1 −  1 −
(x − z)3 (x − y)2 ⇒ = . y − z ( 2 − )3 (− )2 1 1 − 0,25
⇒ (x − z)3 = (x − y)2 8 ( y − z)
Vậy (x − z)3 = (x − y)2 8 ( y − z) .
a) Cho a,b là các số nguyên dương chứng minh biểu thức ab( 2 a + )( 2
2 b + 2) luôn chia hết cho 9.
Nếu a3thì a( 2 a + 2)3 Câu 3 0,5 2,0 Nếu a /3thì 2 a :3 dư 1 2 nên 2
a + 2 hay a(a + 2)3 điểm Suy ra a( 2
a + 2)3với mọi số nguyên dương a 1) 0,25 Tương tự b( 2
b + 2)3với mọi số nguyên dương b Suy ra ab( 2 a + )( 2
2 b + 2) luôn chia hết cho 9. 0,25
b) Tìm số cặp số tự nhiên ( ;x y), y là chữ số biết:
1+ 2 + 3+ 4 +...+ (x −1) = yyy − x
Ta có : 1+ 2 + 3+ 4 +...+ (x −1) = yyy − x
1+ 2 + 3+ 4 +...+ (x −1) + x = yyy 0,25 Mà: x(x 1) 1 2 3 4 ... x + + + + + + = và yyy = .111 y = .3.37 y 2 x(x +1) ⇒ = .3.37 y
⇒ x(x +1) = 2.3.37.y 2
⇒ x(x +1) chia hết cho 37 0,25
⇒ x hoặc x +1chia hết cho 37 ( vì (x, x +1)=1) (1)
2) Ta có: 𝑥𝑥(𝑥𝑥+1) = 𝑦𝑦𝑦𝑦𝑦𝑦
����� ≤ 999 ⇒ 𝑥𝑥(𝑥𝑥 + 1) ≤ 1998 ⇒ 𝑥𝑥 < 2 45 (2) 0,25
Từ (1) và (2) suy ra x = 37 hoặc 𝑥𝑥 + 1 = 37
+) Với x = 37 thì 𝑦𝑦𝑦𝑦𝑦𝑦
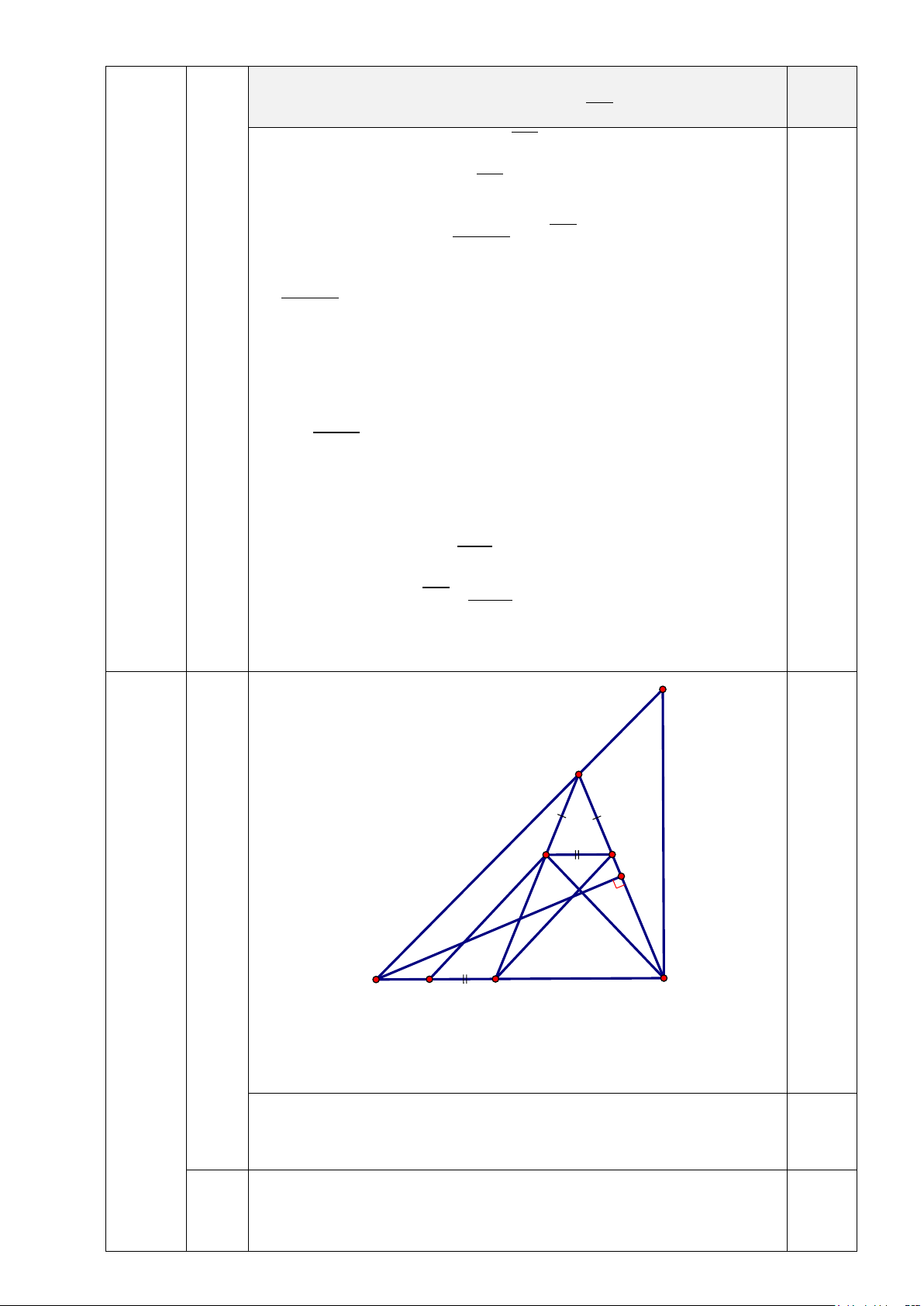
����� = 37.38 = 703 (không thỏa mãn) 2 +) Với x +1= 37 thì 36.37 yyy = = 666 (thỏa mãn) 0,25 2 Vậy( ;x y)= (36;6) N Câu 4 3,0 A điểm 0,25 E D F M I B C
a) Chứng minh MA ∆ C cân tại M  0,5 ° ⇒ = − 
AMC 180 2ACB (1) Lại có: A
∆ BC cân tại A  ° ⇒ = − 
BAC 180 2ACB (2) 0,5
Từ (1) và (2) suy ra  =  AMC BAC . 𝐴𝐴𝐷𝐷𝐴𝐴 � = 𝐶𝐶𝐴𝐴𝐶𝐶
� (kề bù với hai góc bằng nhau) 0,5 Xét B ∆ MA và A ∆ NC có: 0,5
BM = AN (GT );
b) AB= AC(GT);  = 
ABM CAN (chứng minh trên) Suy ra B ∆ MA = A
∆ NC ( .cg.c) . ⇒ MA = NC
Vì AD = AE nên tam giác ADE cân tại A và DC = BE
Ta có tam giác AED và ABC cân tại A nên   0  180 AE B C D AB A C − = = 0,25 2 Suy ra DE//BC
Xét tam giác BIE và EDB có: BI = DE  = 
EBI BED (do DE//BC ) 0,25 BE : cạnh chung.
Suy ra ∆BIE = ∆EDB( .cg.c) ⇒ EI //DB c) Xét B ∆ DE và C ∆ ED có: DC = BE ED là cạnh chung  =  BED CDE 0,25 Suy ra B ∆ ED = C
∆ DE ( .cg.c) ⇒ BD = CE ( ) 1 . Lại có: B ∆ IE = E
∆ DB ⇒ IE = DB(2)
Từ (1) và (2) suy ra CE = IE = BD .
Áp dụng bất đẳng thức tam giác trong tam giác EIC ta có:
EI + EC > IC = IB + BC = DE + BC . 0,25 Hay 2 DE BC BD DE BC BD + > + ⇒ > . Vậy BC DE BD + > ⋅ 2 2
Cho các số nguyên dương ; a ;
b c thỏa mãn a + b + c = 2023. Chứng
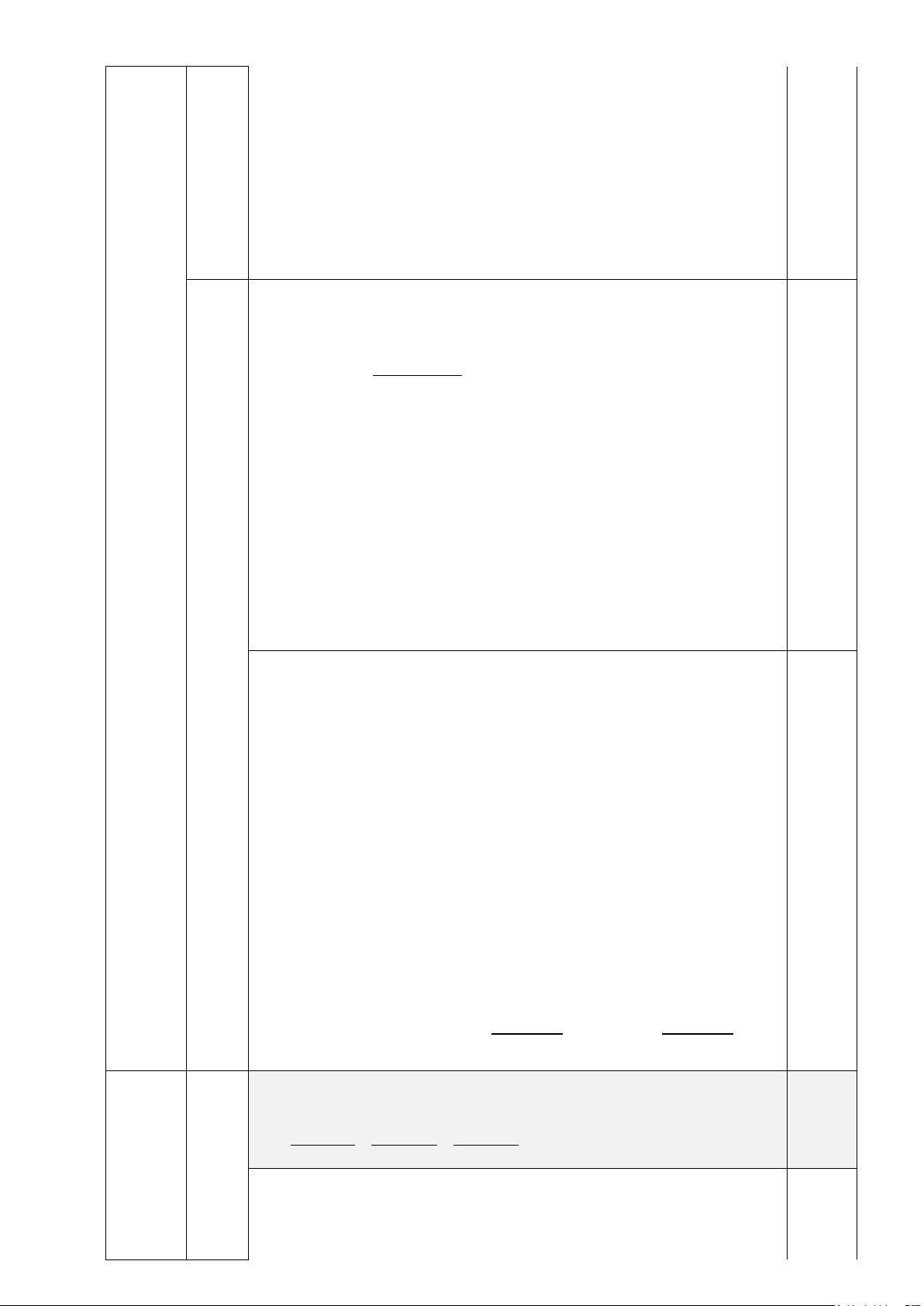
minh rằng giá trị biểu thức sau không phải là một số nguyên: a b c Câu 5 A = + +
2023− c 2023− a 2023− b 1,0
2023 − c = a + b điểm
Theo bài ra ta có a b c 2023  + + =
⇒ 2023− a = b + c 0,25
2023−b = a +  c a b c a b c A = + + = + +
2023− c 2023− a 2023− b a + b b + c a + c
Vì a,b,c là các số nguyên dương nên a b c a b c a + b + c + + > + + = = 1 0,25
a + b b + c a + c a + b + c b + c + a a + c + b a + b + c
Chứng minh: a <1 a a + m ⇒ < b b b + m 0,25
Ta có a ; b ; c <1 nên
a + b b + c a + c a b c a + c b + a c + b
2.(a + b + c) + + < + + = = 2 0,25
a + b b + c a + c a + b + c b + c + a a + c + b a + b + c
Vì 1< A < 2 nên A không phải là một số nguyên.
*Lưu ý: Học sinh làm cách khác nếu đúng yêu cầu của bài vẫn cho điểm tối đa.
Document Outline

• Môn: Toán – Lớp 7