Đề thi Olympic Toán 8 năm 2016 – 2017 phòng GD&ĐT Thanh Oai – Hà Nội
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề thi Olympic Toán 8 năm 2016 – 2017 phòng GD&ĐT Thanh Oai – Hà Nội; đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm.
Trích dẫn đề thi Olympic Toán 8 năm 2016 – 2017 phòng GD&ĐT Thanh Oai – Hà Nội:
+ Cho tam giác ABC. Gọi P là giao điểm của ba đường phân giác trong của tam giác đó. Đường thẳng qua P và vuông góc với CP, cắt CA và CB theo thứ tự tại M và N. Chứng minh.
+ Chứng minh rằng giữa ba số nguyên tố lớn hơn 3 luôn tìm được hai số có tổng hoặc hiệu chia hết cho 12.
+ Tìm số tự nhiên n để biểu thức sau là số nguyên tố 12n2 – 5n – 25.
Preview text:
phßng Gi¸o dôc & §µo t¹o §Ò thi olympic líp 8 Thanh oai N¨m häc 2016 - 2017 M«n thi : To¸n §Ò chÝnh thøc
Thêi gian lµm bµi : 120 phót
(kh«ng kÓ thêi gian giao ®Ò ) Bài 1: (5 điểm)
1. Tìm số tự nhiên n để biểu thức sau là số nguyên tố 12n2 – 5n - 25 2. Giải phương trình: a) x3 + 9x3 + 11x – 21 = 0
b) / 2x - x2 – 1/ = 2x - x2 - 1 Bài 2: (4 điểm)
1. Tìm số nguyên dương x, y sao cho: x3 + y3 + 4(x2 + y2 ) + 4 (x + y ) = 16xy 4 4 x y 1
2. Cho a, b, x, y thỏa mãn: a b a b 2 2 x y 1 2016 2016 x y 2 Chứng minh rằng: 1008 1008 1008 a b (a b) Bài 3: (5 điểm) 27 12x
1. Tìm giá trị nhỏ nhất của biểu thức: A = 2 x 9
2. Cho a, b, c là các số thực dương thỏa mãn điều kiện abc = 1
Tìm giá trị lớn nhất của biểu thức: 1 1 1 P = 2 2 2 2 2 2
a 2b 3 b 2c 3 c 2a 3 Bài 4: (5 điểm)
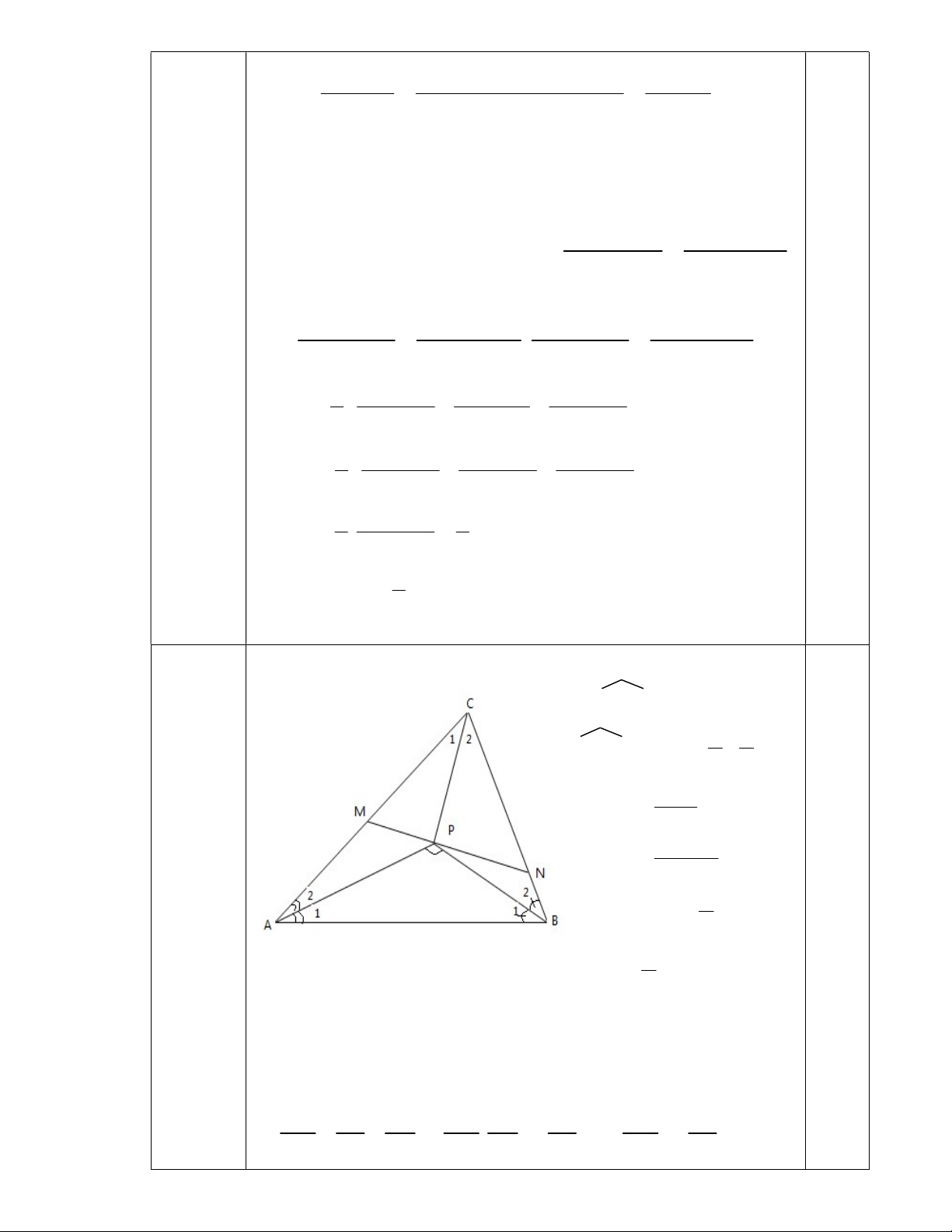
Cho tam giác ABC. Gọi P là giao điểm của ba đường phân giác trong của
tam giác đó. Đường thẳng qua P và vuông góc với CP, cắt CA và CB theo thứ
tự tại M và N. Chứng minh: a) Δ AMP ~ Δ APB 2 b) AM AP BN BP
c) BC.AP2 + AC.BP2 + AB.CP2= AB. AC.BC Bài 5: (1 điểm)
Chứng minh rằng giữa ba số nguyên tố lớn hơn 3 luôn tìm được hai số có
tổng hoặc hiệu chia hết cho 12.
------------------------ Hết --------------------------
(Cán bộ coi thi không giải thích gì thêm) PHÒNG GD&ĐT THANH OAI HD CHẤM THI OLYMPIC LỚP 8 NĂM HỌC 2016-2017 MÔN THI: TOÁN 8
Thời gian làm bài:120 phút Câu Nội dung Điểm Câu 1
1, A= 12n2 – 5n - 25 = (4n + 5)(3n-5) 0,5đ.
( 5 điểm) A là số nguyên tố và 4n + 5 > 0 -> 3n – 5 > 0 , 4n + 5 > 3n – 5
-> A là số nguyên tố -> 3n – 5 = 1 -> n = 2
Có A = 12.22 – 5.2 – 25 = 13 là số nguyên tố 0,5đ.
2, a/ x3 + 9x2 + 11x – 21 = 0
<-> ( x3-1) + ( 9x2 – 9) + ( 11x – 11) = 0 1,0đ.
<-> ( x – 1)(x2 + x + 1) + 9(x+1)(x-1)+ 11(x-1)= 0
<-> ( x – 1 )(x + 3 ) ( x + 7 ) = 0
-> x = 1 hoặc -3 hoặc -7 1,0đ.
b/ / 2x - x2 – 1/ = 2x - x2 - 1
Do 2x - x2 – 1 = - (x – 1 ) 2 0 1,0đ.
Pt <-> x2 - 2x + 1 = 2x - x2 – 1 <-> x = 1 1,0đ. Câu 2
1) pt = ( x3 - 4x2+ 4x) + (y3 - 4y2+ 4y) + ( 8x2 + 8y2 -16xy) = 0 1,5đ.
(4 điểm) <-> x( x - 2)2 + y( y - 2)2 + 8(x – y)2 = 0 (1)
Do x( x - 2)2 0 , y( y - 2)2 0, 8(x – y)2 0 (2)
Từ (1), (2) -> x = y = 2 1,5đ. 4 4 x y 1 (1) 2) a b a b 2 2 x y 1(2) x y 2 2 2 4 4 x y Thay (1) = 2 2 2 (x y ) vào (1) có 0,5đ. a b a b 2 2 2 2 x y x y 1 ... <-> bx2 = ay2 -> a b a b a b 2016 2016 x y 1 -> 1008 1008 1008 a b (a b) 2016 2016 x y 2 -> 0,5đ. 1008 1008 1008 a b (a b) Câu 3 27 12x 2x 12x 36 2 2 (x 9) ( 5 điểm) (x 6) 1) A = 1 1 2,0đ. 2 2 2 x 9 x 9 x 9
-> Min A = -1 <-> x = 6 0,5đ. 2) Có x y2 2 2 0 x y 2xy 0,5đ. Áp dụng ta có: 2 2 a b 2ab , 2 b 1 2b 1 1 -> 2 2
a 2b 3 2(ab b 1) -> 2 2 a 2b 3 2(ab b 1) 1,0đ Tương tự: 1 1 1 1 , 2 2 b 2c 3 2bc c 2 2 1 c 2a 3 2(ac a 1) 1 1 1 1 P
2 ab b 1 bc c 1 ac a 1 1 1 ab b =
2 ab b 1 b 1 ab 1 ab b 1 ab b 1 1 . 2 ab b ( Do abc = 1) 1 2 1 -> P max <-> a = b = c = 1 2 1,0đ. Câu 4 (5 điểm) a) AMP = ˆC = 900 1 ˆ ˆ APB = 1800 - A B 2 2 ˆ ˆ = 1800 - A B 0,5đ. 2 0 ˆ = 1800 - 180 C 2 ˆ C = 0 0 180 90 2 ˆ C = 0 ˆ ˆ 90 , A A 1 2 2 -> Δ AMP ~ Δ APB 1,5đ. (g.g)
b) Tương tự Δ APB ~ Δ PNB 0,5đ. 2 2 AM AP PN AM PN AP AM AP -> . MP PB NB MP NB BP NB BP 1,5đ. AM PN c) Δ AMP ~ Δ PNB -> MP NB
-> AM . NB = PN . MP = MP2
-> AM . NB = CM2 – CP2 = (CA – AM )(CB – BN) – CP2
= CA.CB – CA.BN – AM.CB + AM.BN – CP2
-> AM.CB + BN.CA + CP2 = CA.CB 0,5đ.
-> AM.CB.AB + BN.CA.AB + CP2 .AB = AB.BC.CA (1) AM AP Từ Δ AMP ~ Δ APB -> 2 AM .AB AP (2) AP AB BN BP Tương tự 2 BN.AB BP (3) BP AB
Từ (1), (2), (3) -> đpcm 0,5đ. Câu 5
Một số nguyên tố lớn hơn 3 khi chia cho 12 thì chỉ có thể có số
(1 điểm) dư là 1; 5; 7; 11 chia tập hợp số nguyên tố thành 2 tập hợp con. A
là tập hợp số nguyên tố chia 12 dư 1 hoặc 11, B là tập hợp số
nguyên tố chia 12 dư 5 hoặc 7. Vì có 3 số nguyên tố mà chỉ thuộc
một trong 2 tập hợp A hoặc B. Nên theo nguyên tắc đirichle phải
có 2 số thuộc cùng một tập hợp, 2 số này có tổng hoặc hiệu chia hết cho 12 1,0đ.
*Chú ý :Học sinh có thể giải cách khác, nếu chính xác thì vẫn cho điểm.