Đề thi thử HSG lần 2 Toán 7 năm 2022 – 2023 phòng GD&ĐT Hiệp Hòa – Bắc Giang

UBND HUYỆN HIỆP HÒA
ĐỀ THI THỬ HỌC SINH GIỎI CẤP HUYỆN LẦN 2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022 - 2023 MÔN: TOÁN 7 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút (Không kể thời gian giao đề) Câu 1 (5,0 điểm): 2  
1) Thực hiện phép tính:  1   1   1 6.  3.  1 : 1 − − − + − −  3 3   3         12 5 6 2 10 3 5 2 2) Rút gọn biểu thức: 2 .3 4 .9 5 .7 25 .49 A − − = ( − 2 2 .3)6 (125.7)3 9 3 + 5 .14 3) Tìm x biết: 1 4 x − + = (− ) 2 3,2 + 3 5 5 Câu 2 (4,0 điểm): 2 2 1) Cho +
a,b,c là ba số khác 0 thỏa mãn 2
b = ac . Chứng minh rằng a b a = . 2 2 b + c c 2) Cho 1 1 1 A = + +.....+
. Chứng minh rằng A < 25. 2 4 9 1000 36 Câu 3 (4,0 điểm):
1) Tìm số nguyên a để 2
a + a + 3 chia hết cho a +1.
2) Tìm các số nguyên tố x, y thỏa mãn 2 2 x − 2y =1. Câu 4 (6,0 điểm):
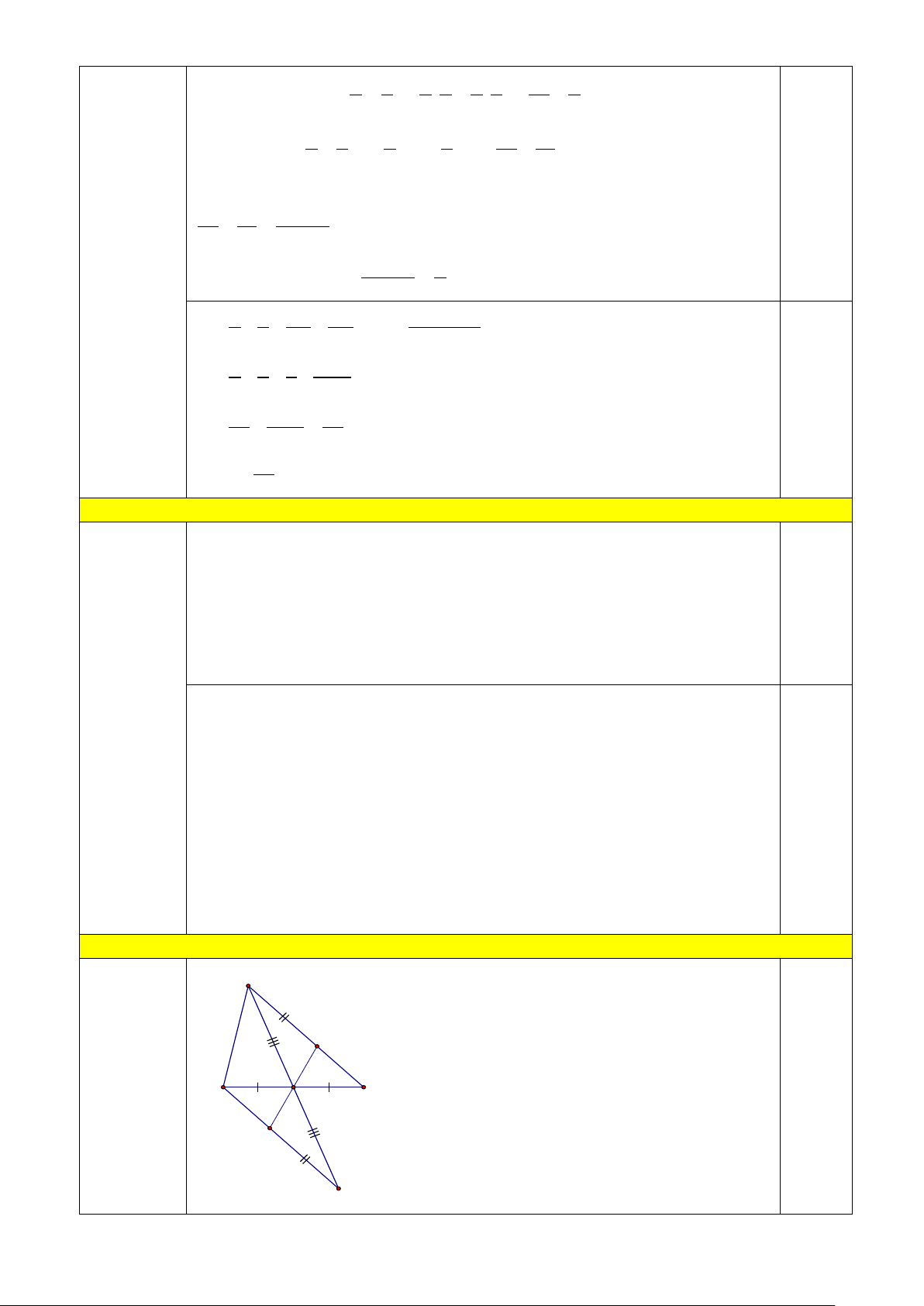
1) Cho tam giác ABC có M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy
điểm E sao cho ME = MA.
a) Chứng minh AC / /BE .
b) Gọi I là một điểm trên đoạn thẳng AC, K là một điểm trên đoạn thẳng EB sao cho
AI = EK . Chứng minh ba điểm I, M, K thẳng hàng.
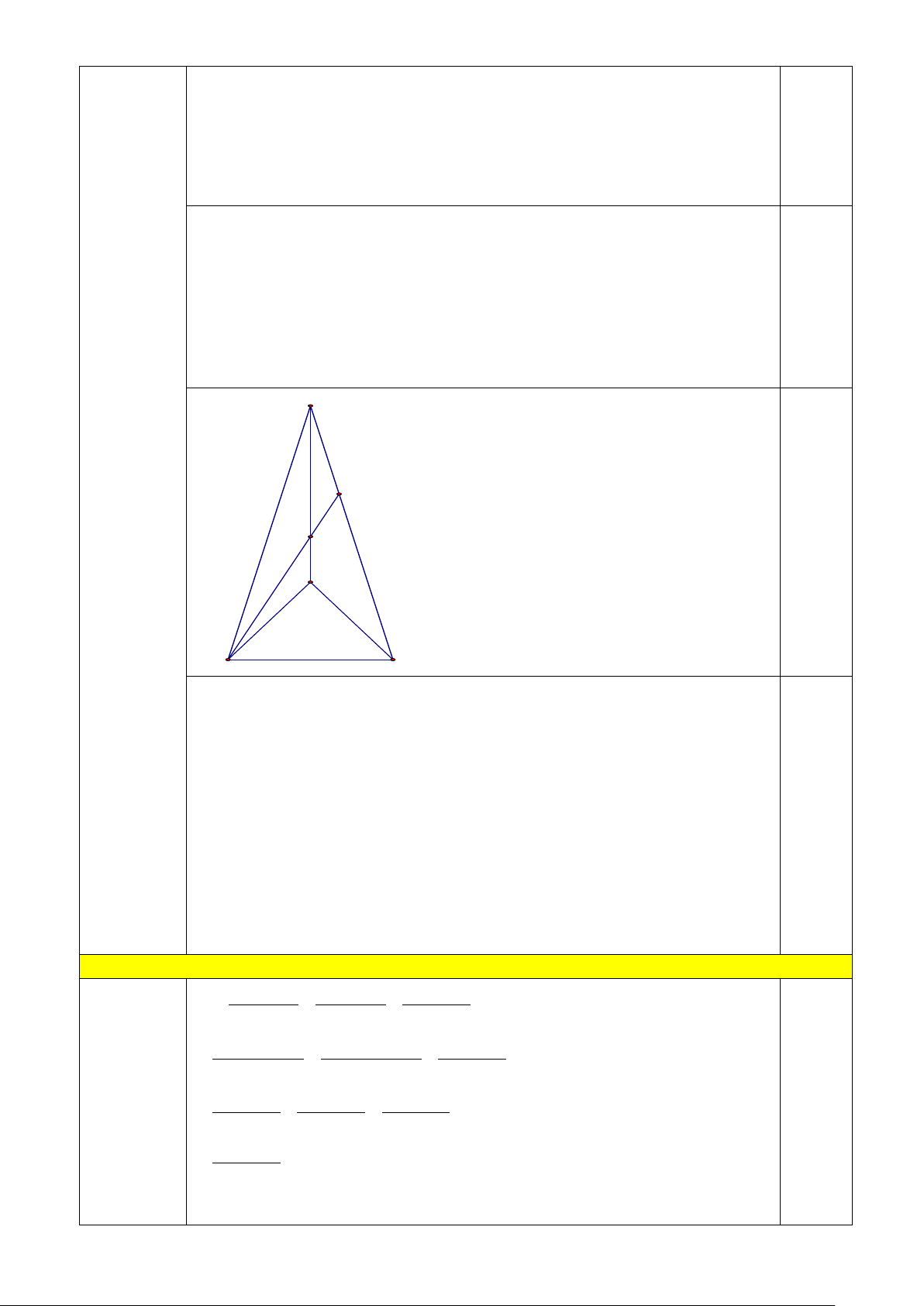
2) Cho tam giác ABC cân tại A có  0
BAC = 20 . Vẽ tam giác đều BCD sao cho điểm D
nằm trong tam giác ABC. Tia phân giác của 
ABD cắt AC tại M. Chứng minh AM = BC . Câu 5 (1,0 điểm):
Cho xyz =1. Tính giá trị của biểu thức x y z A = + + .
xy + x +1 yz + y +1 xz + z +1
...............Đề gồm 01 trang...............
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HDC ĐỀ THI THỬ HỌC SINH GIỎI HUYỆN NĂM HỌC: 2022-2023 Môn thi: Toán 7 Câu Nội dung Điểm Câu 1 2  1 1       1 
(5,0 điểm) 1) 6. − −   3. − +   1 : − −  1  3 3   3          1   1 3 6. 1 1 :  = + + − − 0,5  9     3 3  2   4 0,5 2 :  = + − 3     3  0,5 2 6  4 :  = + −  3 3    3  8 3 . − = = 2 − 0,5 3 4 12 5 6 2 10 3 5 2 2) 2 .3 4 .9 5 .7 25 .49 A − − = ( − 2 2 .3)6 (125.7)3 9 3 + 5 .14 12 5 12 4 10 3 10 4 2 .3 − 2 .3 5 .7 − 5 .7 = − 0,5 12 6 9 3 9 3 3 2 .3 5 .7 + 5 .7 .2 12 4 2 .3 (3− ) 10 3 1 5 .7 (1− 7) = − 12 6 9 3 2 .3 5 .7 ( 3 1+ 2 ) 0,5 12 4 10 3 2 .3 .2 5 .7 ( 6 − ) = − 12 6 9 3 2 .3 5 .7 .9 0,5 2 5.( 6 − ) 2 30 − 32 = − = − = 2 3 9 9 9 9 3) 1 4 x − + = (− ) 2 3,2 + 3 5 5 1 4 16 2 ⇒ x − + = − + 3 5 5 5 0,5 1 4 14 ⇒ x − + = − 3 5 5 1 4 14 ⇒ x − + = 3 5 5 1 14 4 ⇒ x − = − 1 ⇒ x − = 2 3 5 5 3 1 ⇒ x − = 2 hoặc 1 x − = 2 − 0,5 3 3 1 ⇒ x = 2 + hoặc 1 x = 2 − + 3 3 7 ⇒ x = hoặc 5 x = − 3 3 Vậy 7 5 x  ;  ∈ − 3 3   0,5 Câu 2 2 2 a b a a a b a a
(4,0 điểm) 1) Ta có b = ac ⇒ = ⇒ . = . ⇒ = 1 2 ( ) b c b b b c b c 0,5 2 2 2 2 Mặt khác, từ a b  a   b  a b = ⇒ = ⇒ =     0,5 2 2 b c  b   c  b c
Theo tính chất của dãy tỉ số bằng nhau, ta có: 0,5 2 2 2 2 a b a + b = = 2 2 2 2 2 ( ) b c b + c 2 2
Từ (1) và (2) suy ra a + b a = (đpcm) 0,5 2 2 b + c c 1 1 1 1 1 0,5 A < + + + + .....+ 4 9 3.4 4.5 999.1000 1 1 1 1 0,5 A < + + − 4 9 3 1000 25 1 25 0,75 A < − < 36 1000 36 25 0,25 Vậy A< 36
Câu 3 1) Ta có : 2a+a+3 chia hết cho a+1⇒a(a+ )1+3    (a + ) 1 ( ) 1
(4,0 điểm) Vì a là số nguyên nên 0,5 a(a + ) 1  (a + ) 1 (2)
Từ (1) và (2) suy ra 3  (a + )
1 hay a +1 là các ước của 3 0,5 Do đó a +1∈{ 3 − ;−1;1; } 3 ⇒ a ∈{ 4; − − 2;0; } 2 Vậy 0,5 a ∈{ 4; − − 2;0; }
2 là các giá trị nguyên cần tìm. 0,5 2) Từ 2 2
x − 2y =1 suy ra 2 2 x −1 = 2y ( ) 1
+ Nếu x chia hết cho 3 mà x là số nguyên tố nên x = 3
Thay x = 3 vào (1) ta được: 0,5 2 2
2y = 8 ⇒ y = 4 ⇒ y = 2 (vì y là số nguyên tố) 0,5
+ Nếu x không chia hết cho 3 thì 2
x chia cho 3 dư 1 nên 2 x −1 chia hết
cho 3. Do đó từ (1) suy ra 2 2y chia hết cho 3 Mà (2;3) =1 nên 2
y  3 ⇒ y  3 ⇒ y = 3 (vì y là số nguyên tố) 0,5
Thay y = 3 vào (1) ta được 2 2
x −1 =18 ⇒ x =19 ⇒ x ∉ Z (loại)
Vậy có duy nhất cặp số nguyên tố (x, y) thỏa mãn đề bài là (3;2). 0,5 Câu 4 A (6,0 điểm) I B C M K E a) Xét A ∆ MC và E ∆ MB có:
MC = MB (gt),  = 
AMC EMB (hai góc đối đỉnh), MA = ME (gt) ⇒ A ∆ MC = E ∆ MB (c.g.c) ⇒  = 
CAM BEM (hai góc tương ứng) 1,5 Mà  CAM và 
BEM là hai góc so le trong nên AC / /BE (đpcm). 0,5 b) Xét A ∆ MI và E ∆ MK có:
AI = EK (gt),  = 
IAM KEM (theo ý a), MA = ME (gt) ⇒ A ∆ MI = E ∆ MK (c.g.c) 1,0 ⇒  = 
AMI EMK (hai góc tương ứng) (1) Mà  +  0
AMK EMK =180 (hai góc kề bù) (2) 1,0
Từ (1) và (2) suy ra  +  0 = ⇒  0 AMK IMA 180 IMK =180
Hay ba điểm I, M, K thẳng hàng (đpcm). A M O D C B 2) Chứng minh A ∆ DB = A
∆ DC (c.c.c) suy ra  =  DAB DAC Do đó  0 0 DAB = 20 : 2 =10 + A
∆ BC cân tại A, mà  0 BAC = 20 (gt) nên  0 0 0
ABC = (180 − 20 ) : 2 = 80 0,5 + B
∆ CD là tam giác đều nên  0 DBC = 60
+ Tia BD nằm giữa hai tia BA và BC suy ra  0 0 0 ABD = 80 − 60 = 20 .
+ Tia BM là phân giác của  ABD nên  0 ABM =10 0,5
+ Xét tam giác ABM và BAD có:
AB cạnh chung ;  =  0 =  =  0
BAM ABD 20 ; ABM DAB =10 Vậy: A ∆ BM = B ∆ AD (g.c.g) 0,5
suy ra AM = BD , mà BD = BC (tam giác ABC đều) nên AM = BC 0,5 Câu 5 x y z
(1,0 điểm) A = + +
xy + x +1 yz + y +1 xz + z +1 xz yxz z = + +
z(xy + x +1) xz(yz + y +1) xz + z +1 xz 1 z = + + 0,5
xz + z +1 xz + z +1 xz + z +1 xz + z +1 = = 1 xz + z +1 0,5 Vậy A=1