




Preview text:
TRƯỜNG CHUYÊN LÊ KHIẾT
ĐỀ THI THỬ TỐT NGHIỆP THPT LẦN 1NĂM 2022 Bài thi: TOÁN Thời gian: 90 phút Câu 1.
Cho số phức z 2 3i . Điểm biểu diễn số phức w 2z 1 i z trên mặt phẳng phức là
A. N 1;3 .
B. P 3; 1 . C. Q 3 ; 1 . D. M 3; 1 . Câu 2.
Trong không gian Oxyz , cho ba điểm A2; 1;5, B 5; 5;7 , M ; x y ; 1 . Khi , A B, M thẳng
hàng thì giá trị của x , y là
A. x 4; y 7 .
B. x 4; y 7 .
C. x 4; y 7 .
D. x 4; y 7 Câu 3.
Trong không gian Oxyz , mặt cầu S 2 2 2
: x y z 2x 4y 1 0 có tâm là
A. I 1; 2;0 . B. I 2 ;4;0 . C. I 1 ;2;0. D. I 1 ;2; 1 . Câu 4.
Tập nghiệm của bất phương trình log x + 1 < 3 là 2 ( ) A. S = (- 1; ) 8 .
B. S = (- 1; 7). C. S = (- ¥ ) ;8 .
D. S = (- ¥ ;7). Câu 5.
Cho số phức z thỏa mãn (1+ 2i)z = 3- 4i . Phần ảo của số phức z bằng A. - 4 . B. 2 . C. - 2 . D. 4 . 1 Câu 6.
Tập xác định của hàm số y = ( 2 x - )5 9 1 là æ - 1ö 1 æ ö íï ü = ç ÷ - ¥ Èç ÷ 1 ï ï A. D ; ç ÷ ;+ ¥ ç ÷ ç D = ¡ \ ì ± ý è . 3 ÷ ø è3 ç ÷ø. B. ïî 3ï ï ïþ æ 1ù 1 é ö æ- ö = ç ÷ 1 1 ç ÷ C. D - ¥ ; úÈ ê ;+ ¥ ç ÷ ç D = ; ç ÷ è . D. 3ú 3 ÷ ê ø û ë çè 3 3÷ø. Câu 7.
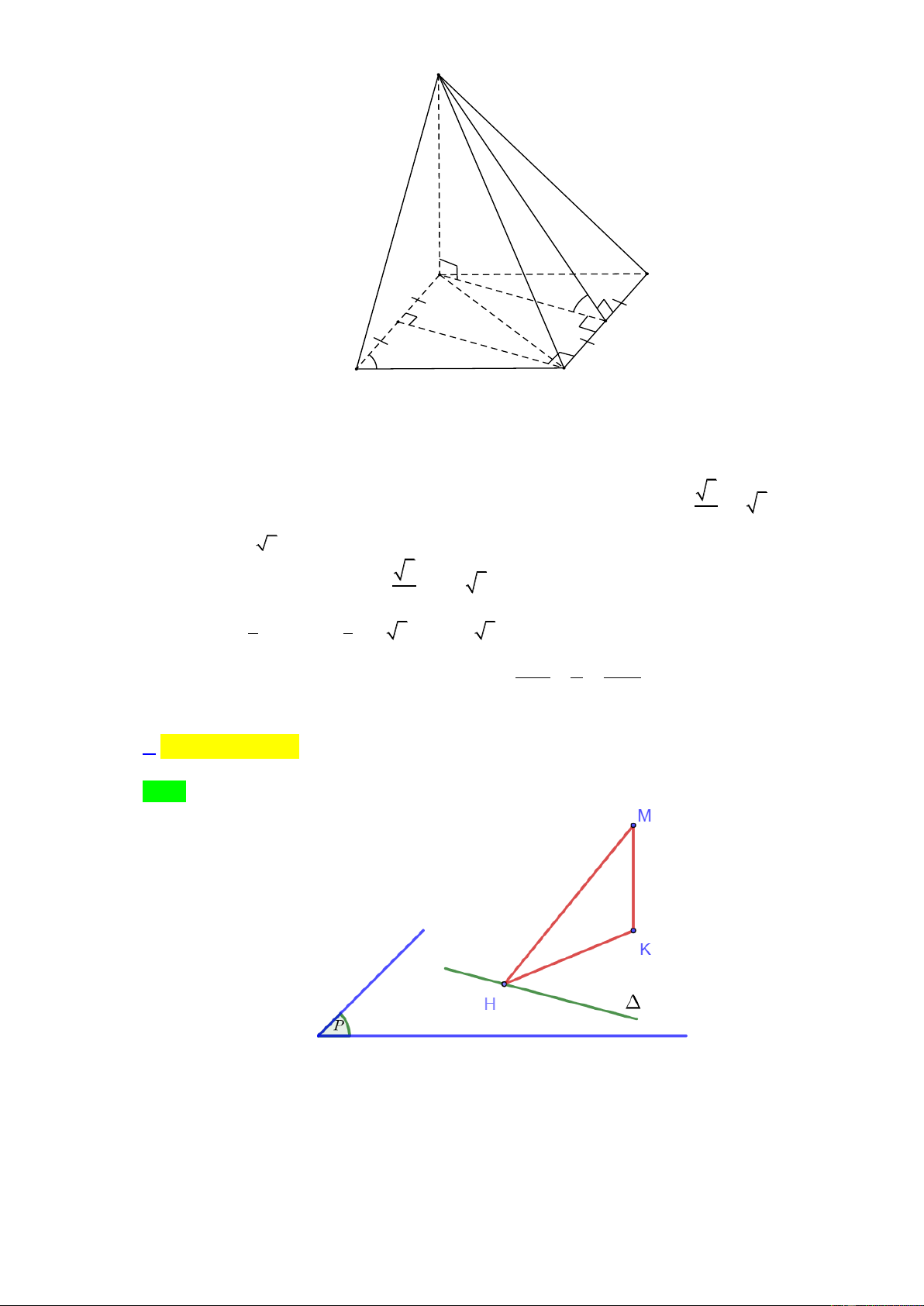
Cho hình chóp S.ABC đáy là tam giác đều cạnh a . Cạnh bên SC vuông góc với mặt phẳng
ABC, SC a. Thể tích khối chóp S.ABCbằng 3 a 3 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 3 12 12 9 1 1 1 Câu 8. Nếu tích phân
f (x)dx = - 2 ò và
g (x)dx = 7 ò thì 2
é f (x)- 3g(x) d ù x ò ë û bằng 0 0 0 A. 25. B. 12. C.17. D. 25. Câu 9.
Trong không gian Oxyz , mặt phẳng P : x y z 3 0 đi qua điểm nào dưới đây?
A. M 1;1; 1 . B. N 1 ; 1 ;1 . C. N 1;1 ;1 . D. Q 1 ;1; 1 .
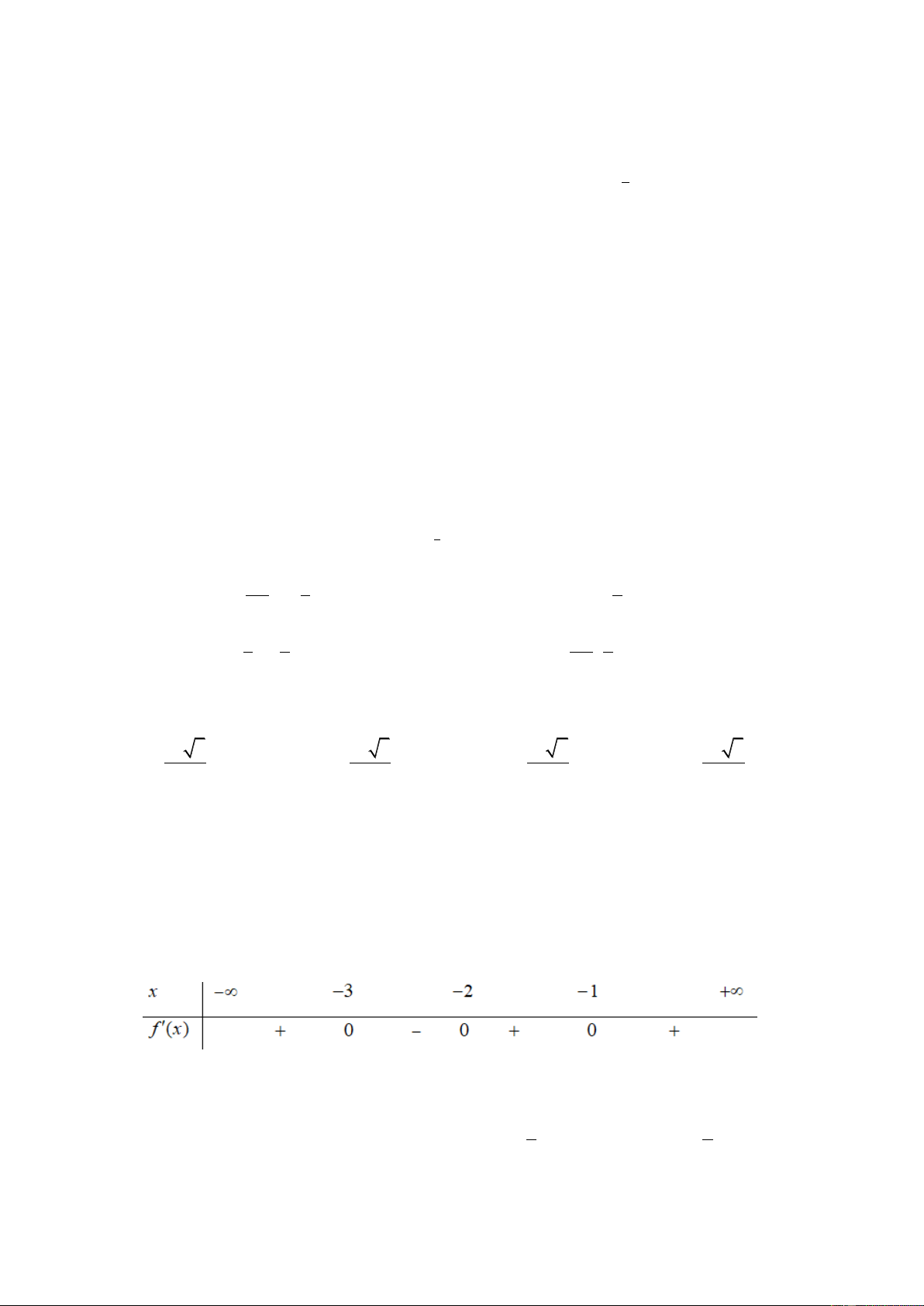
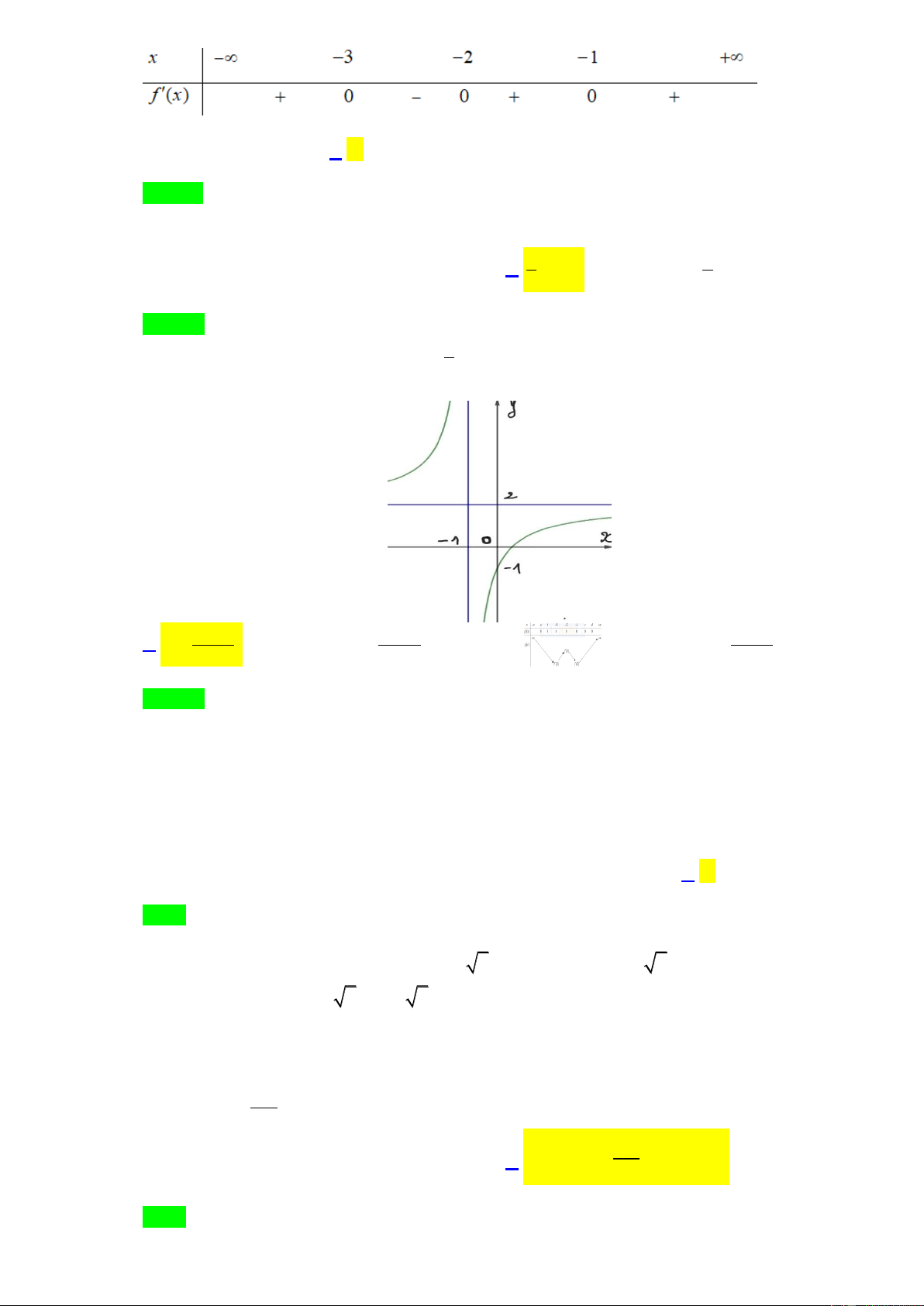
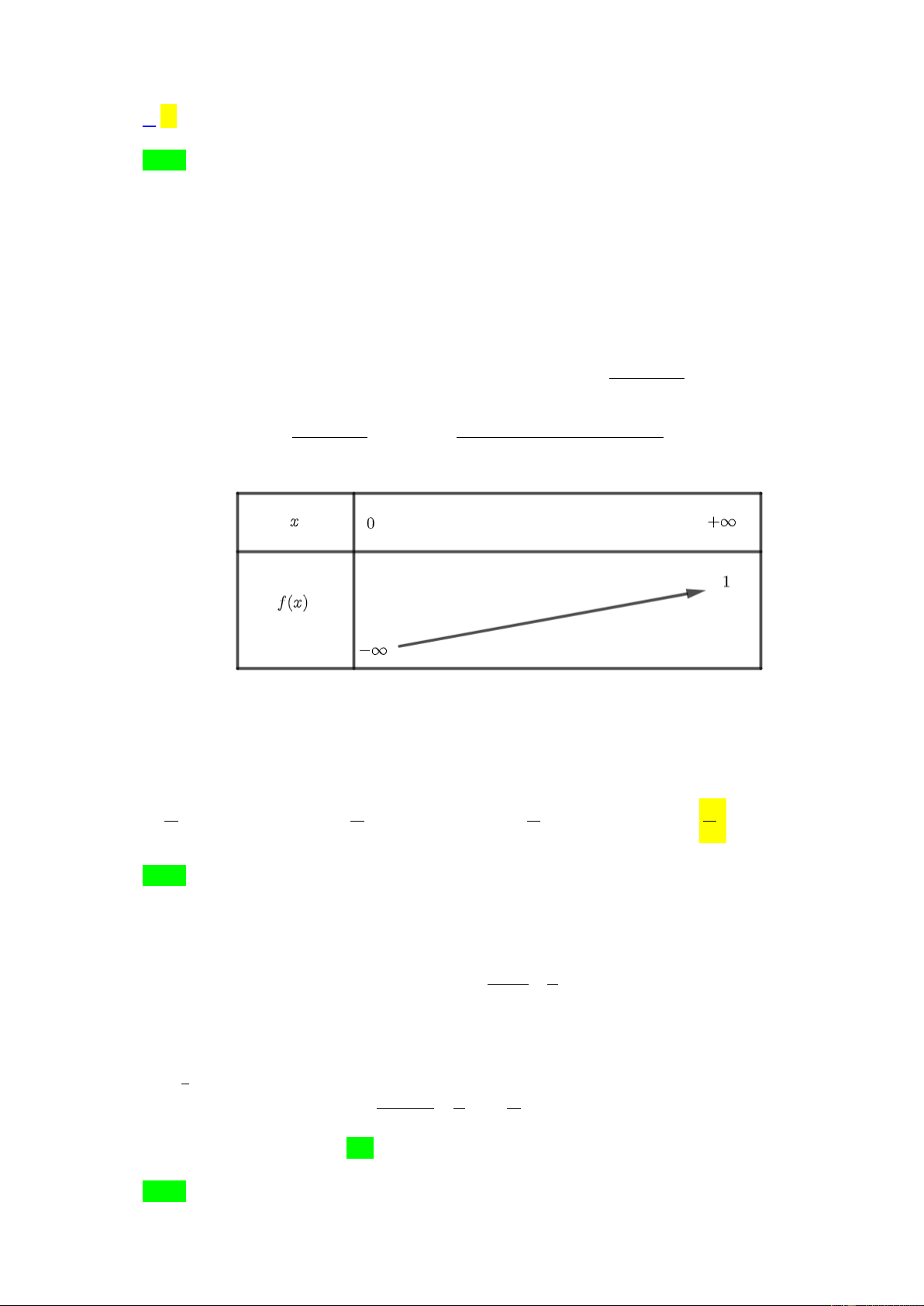
Câu 10. Cho hàm số f x có bảng xét dấu của đạo hàm như sau
Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C.1. D. 5 .
Câu 11. Cho khối nón có chiều cao h và bán kính đáy bằng r . Thể tích của khối nón đã cho bằng 1 4 A. 2 rh . B. 2 r h C. 2 r h . D. 2 r h . 3 3
Câu 12. Hàm số nào dưới đây có đồ thị như hình vẽ bên? Trang1 2x 1 2x 1 1 2x 2x 1 A. y . B. y C. y . D. y . x 1 x 1 x 1 x 1
Câu 13. Tích tất cả các nghiệm của phương trình 2
log x 2log x 7 0 là 3 3 A. 2 . B. 7 . C.1. D. 9 .
Câu 14. Họ nguyên hàm của hàm số f x 3x sin x là A. 2 3x f x dx
cos x C . B. f x 2
dx 3x cos x C . 2 x C. f
xdx 3cosxC . D. f x 2 3 dx
cos x C . 2
Câu 15. Môđun của số phức z 2 3i bằng A. 5 . B. 5 . C. 7 . D. 7 . 5 a
Câu 16. Cho a, b là hai số thực dương và a khác 1 thỏa mãn log
2 . Giá trị của biểu thức log b 3 a a 4 b bằng 1 1 A. 4 . B. . C. 4 . D. . 4 4 x
Câu 17. Tiệm cận ngang của đồ thị hàm số 3 2 y
là đường thẳng có phương trình x 2 2 3 A. y 2 . B. y . C. y 3 . D. y . 3 2 Câu 18. Cho hàm số 4 2
y ax bx cx d có đồ thị như hình dưới. Mệnh đề nào đúng?
A. a 0;b 0; c 0; d 0 .
B. a 0;b 0; c 0; d 0 .
C. a 0;b 0; c 0; d 0 .
D. a 0;b 0; c 0; d 0 .
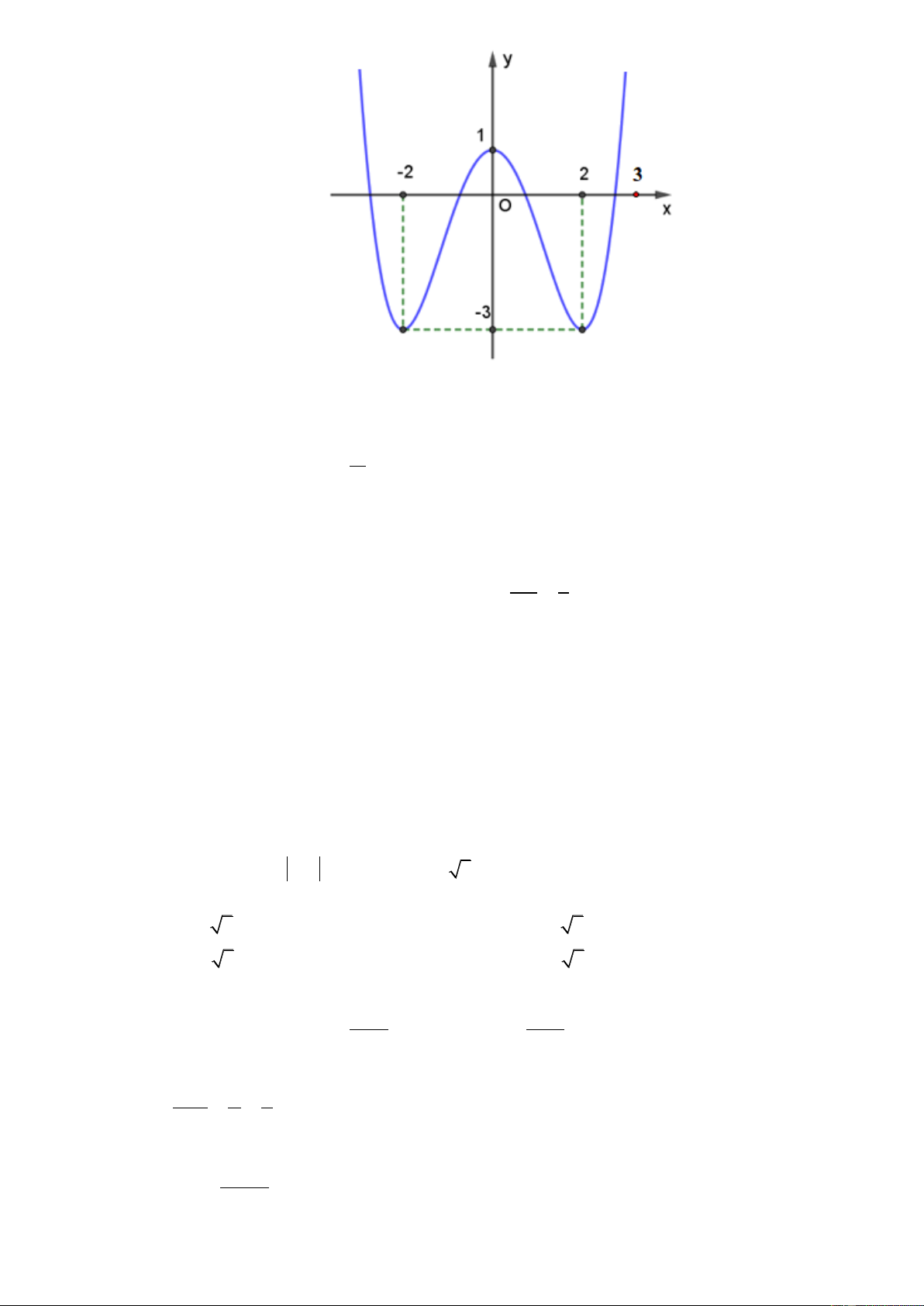
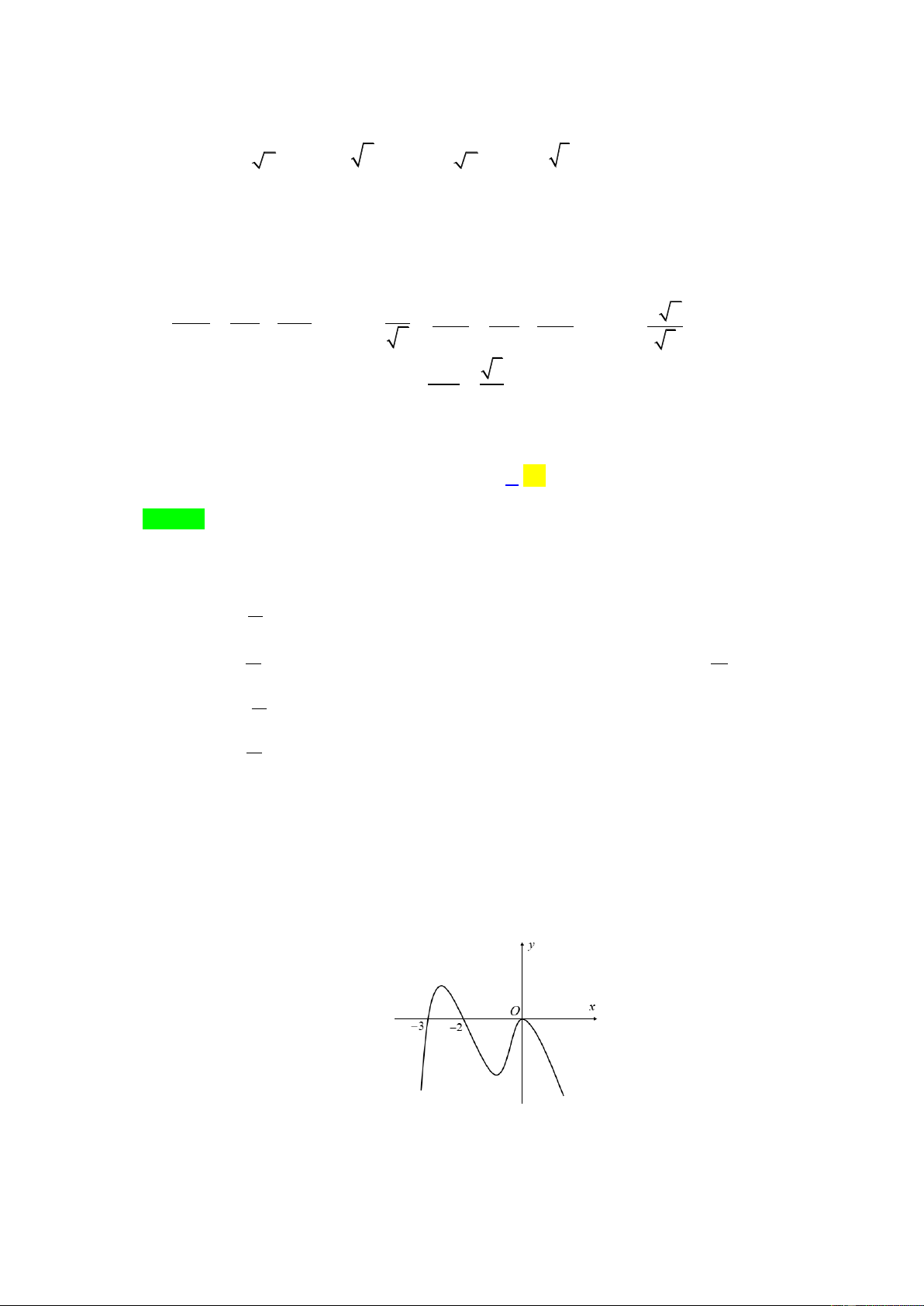
Câu 19. Cho hàm số y f x liên tục trên và có đồ thị là đường cong như hình vẽ bên dưới Trang2
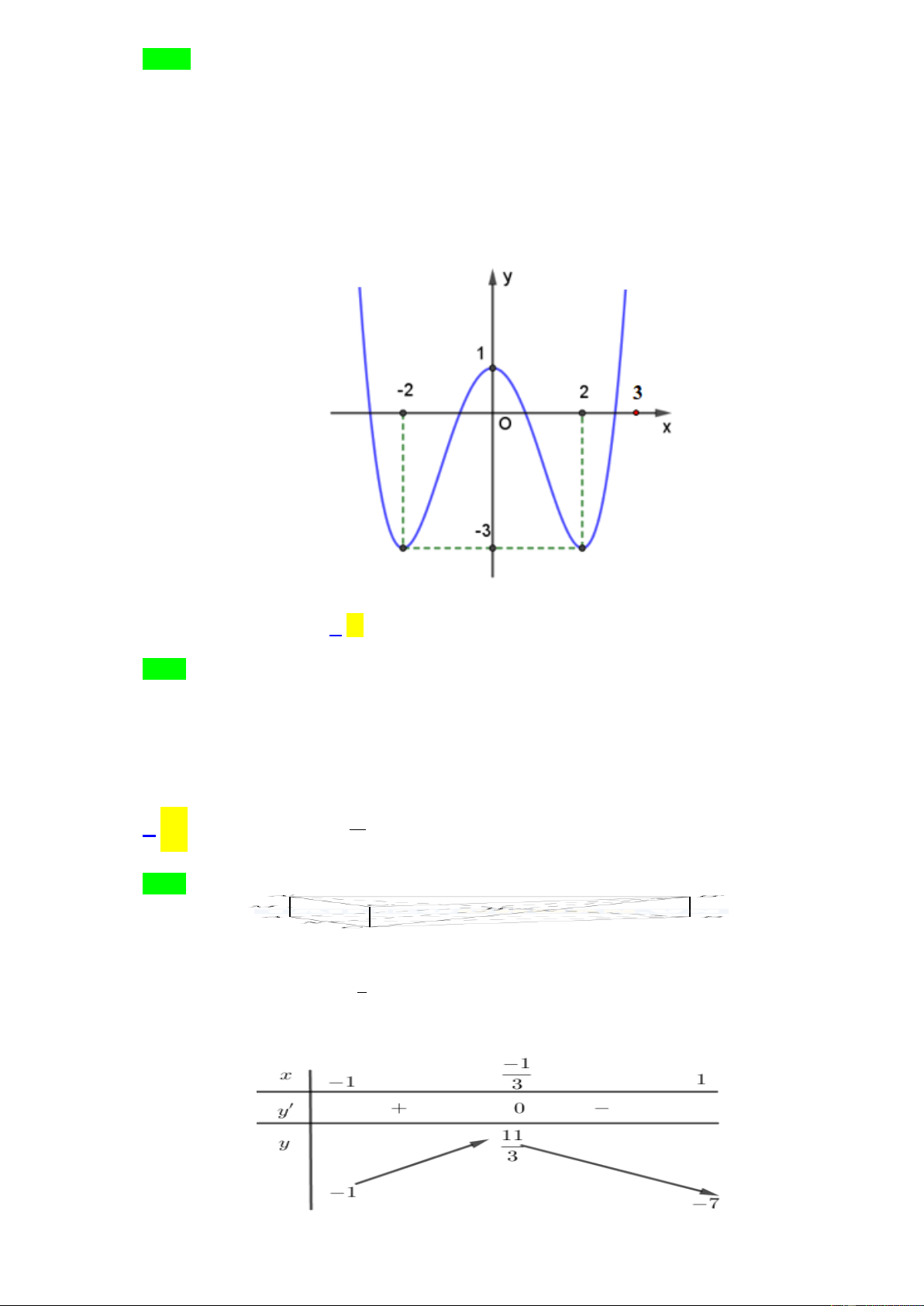
Số nghiệm của phương trình f x 2 0 trên đoạn 2 ;3 là A. 3 . B. 2 . C. 4 . D.1.
Câu 20. Giá trị nhỏ nhất của hàm số y 3cos 2x 4 sin x là: 11 A. 7 . B. . C. 5 . D.1. 3
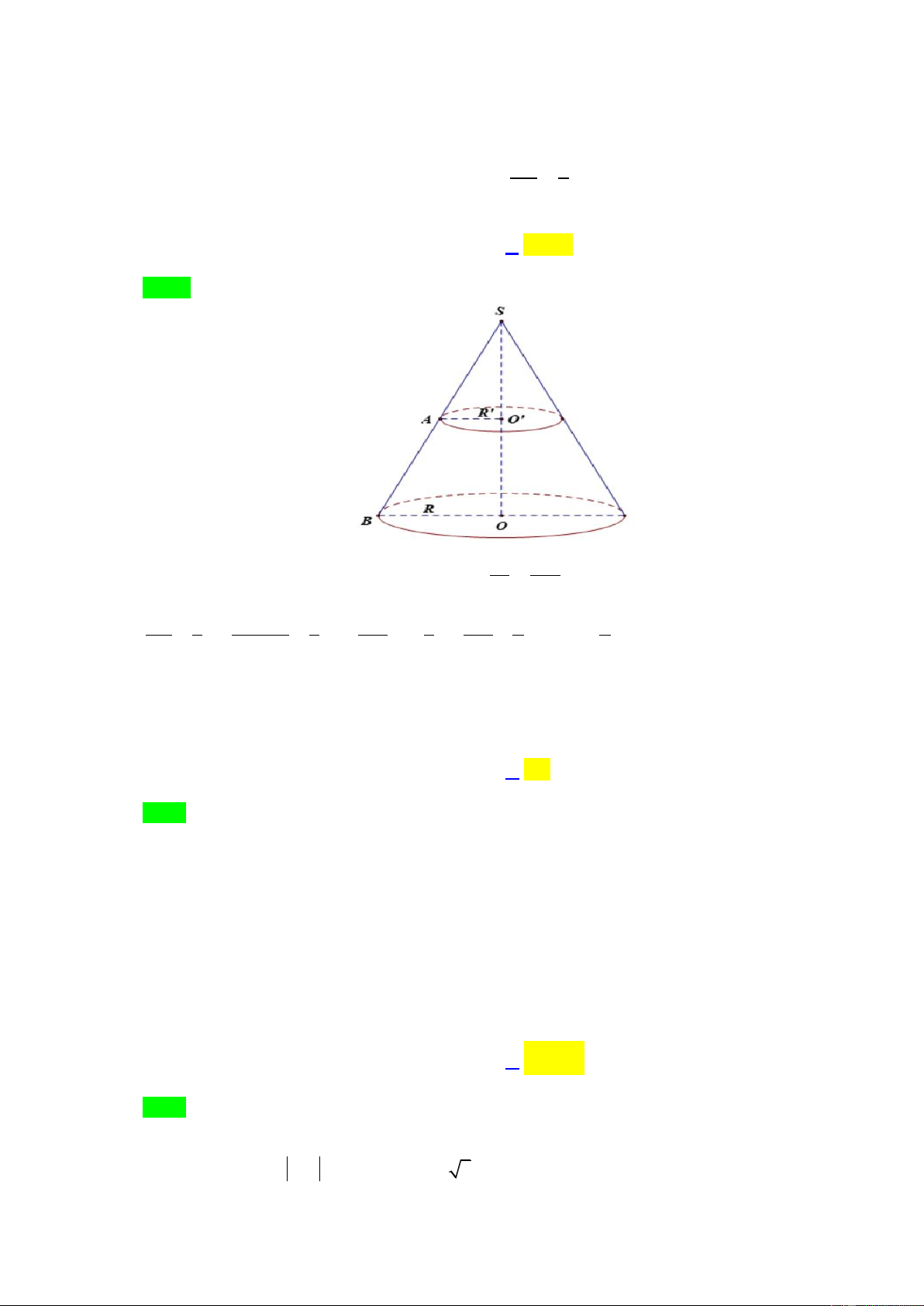
Câu 21. Cho hình nón N đỉnh S đáy là đường tròn C ; O
R , đường cao SO 40cm . Người ta cắt 1
hình nón bằng mặt phẳng vuông góc với trục để đường hình nón nhỏ N có đỉnh S và đáy là 2 VN 1
đường tròn C'O'; '
R .Biết rằng tỉ số thể tích 1
. Độ dài đường cao của hình nón N V 8 2 N2 là: A. 5cm . B.10cm. C. 20cm. D. 49cm.
Câu 22. Cho hàm số f x liên tục trên 3;7 , thoả mãn f x f 10 x với mọi x 3;7 và 7 7 f
xdx 4. Tích phân xf xdx bằng 3 3 A. 80 . B. 60 . C. 20 . D. 40 .
Câu 23. Cho cấp số cộng u với u 10,u 13. Giá trị của u là n 1 2 4 A. u 18 . B. u 16 . C. u 19 . D. u 20 . 4 4 4 4
Câu 24. Cho số phức z có z 1
2 và w 1 3i z 2 . Tập hợp các điểm biểu diễn số phức w là
đường tròn , tâm và bán kính của đường tròn đó là A. I 3 ; 3, R 4 .
B. I 3; 3, R 4 .
C. I 3; 3, R 2 .
D. I 3; 3, R 4 .
Câu 25. Cho log 5 m , log 5 n . Khi đó log 5 tính theo m , n là 2 3 6 mn 1 A. 2 2 m n B. C.
D. m n m n m n
Câu 26. Trong không gian Oxyz , cho mặt phẳng P : x y z 1 0 và đường thẳng x 1 y z d :
. Gọi d là hình chiếu vuông góc của d lên mặt phẳng P . Đường thẳng 1 1 2 1 3 1
d nằm trên P tạo với d , d các góc bằng nhau, d có vectơ chỉ phương u a ; b ; c . Giá trị 2 1 1 2
biểu thức 3a b bằng c Trang3 11 11 13 A. B. C. 4 D. 3 3 3
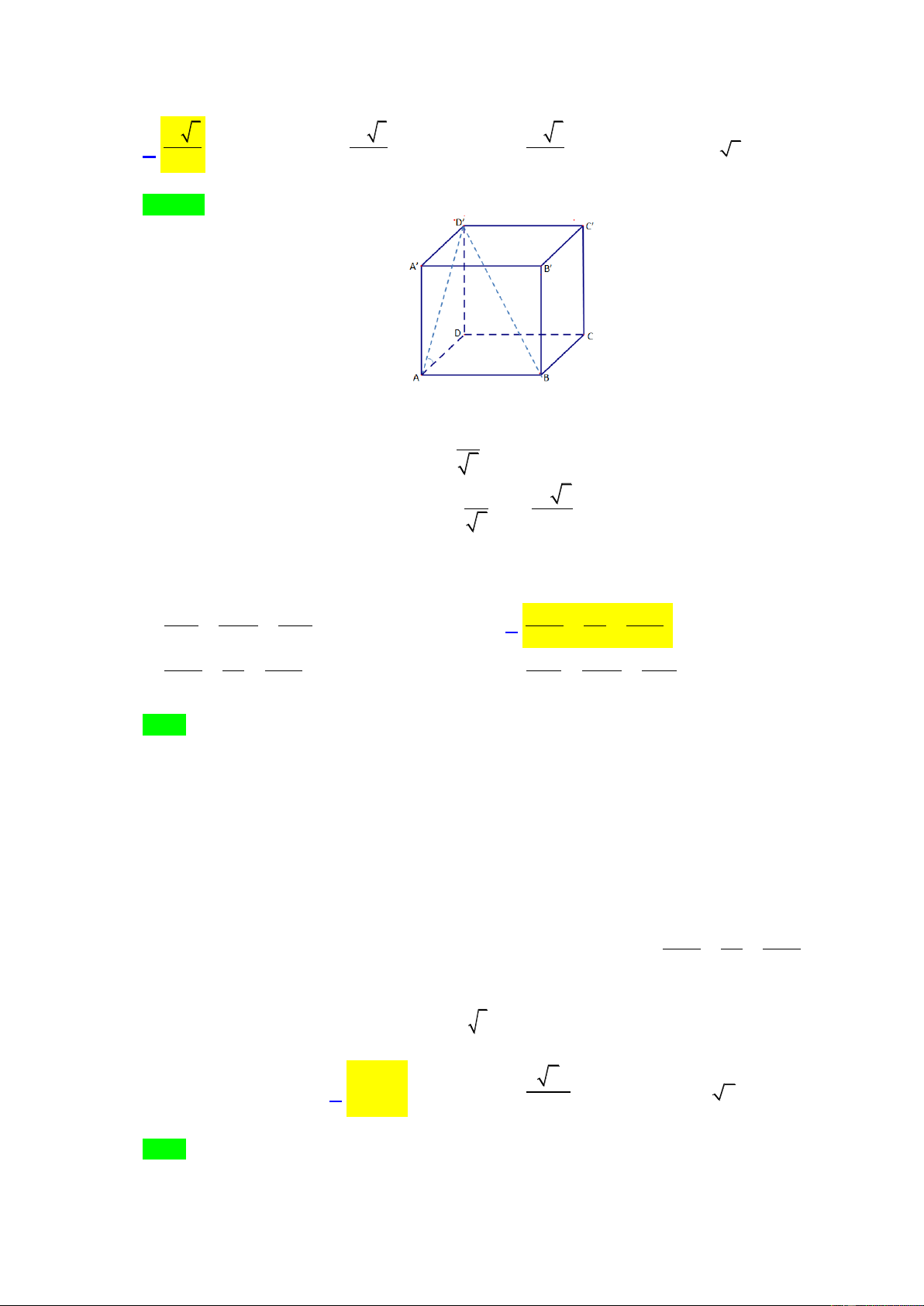
Câu 27. Cho hình hộp đứng ABC . D A B C D
có đáy là hình vuông cạnh a , góc giữa mặt phẳng D AB
và mặt phẳng ABCDlà 30 . Thể tích khối hộp ABC . D A B C D bằng 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a 3 . 3 18 9
Câu 28. Trong không gian Oxyz , phương trình đường thẳng d đi qua A1; 2 ;1 và vuông góc với
P: x2y z 1 0 là x 1 y 2 z 1 x 2 y z 2 A. . B. . 1 2 1 2 4 2 x 2 y z 2 x 1 y 2 z 1 C. . D. . 1 2 1 2 2 1
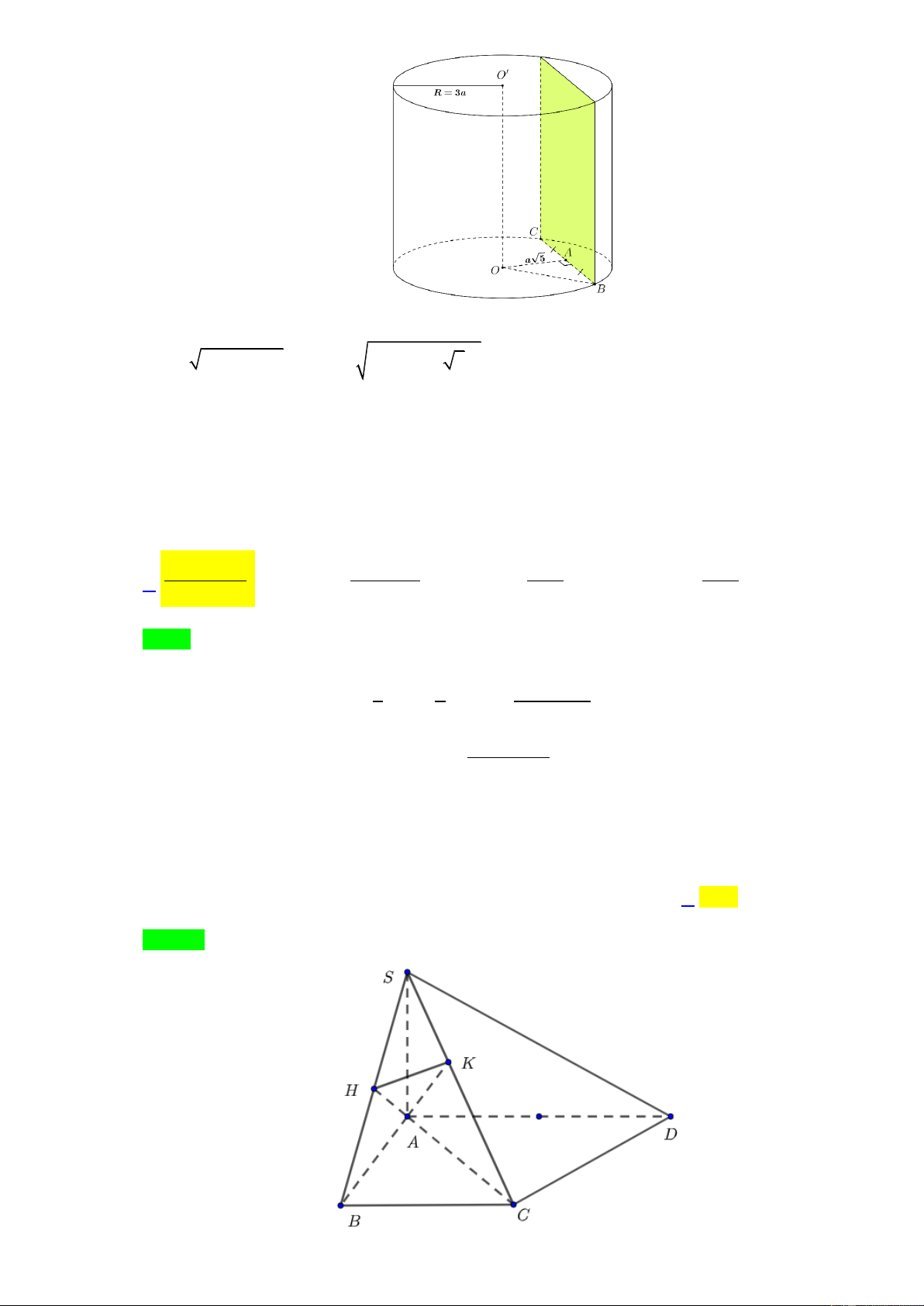
Câu 29. Cho hình trụ có bán kính bằng 3a . Cắt hình trụ bởi mặt phẳng P song song với trục của hình
trụ và cách trục của hình trụ một khoảng a 5 ta được một thiết diện hình vuông. Thể tích của khối trụ đã cho bằng 2 2 A. 3 12 a . B. 3 36 a . C. 3 a . D. 3 2 2 a . 3 x
Câu 30. Một nguyên hàm của hàm số f x 3 1 2 e 2x là 3x 1 3 e 2x 3x 1 3 e x 3x 1 e 3x 1 e 3 3 A. . B. . C. 2x . D. x . 3 3 3 3
Câu 31. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD , SA a , đáy ABCD là hình
thang vuông tại A và B với AB BC a , AD 2a . Góc giữa hai mặt phẳng SBC và
SCD bằng A. 30 . B.150 . C. 90 . D. 60 .
Câu 32. Đồ thị của hàm số 3 2 2
y x 2mx m x n có điểm cực tiểu là I 1; 3. Khi đó m n bằng A. 3. B. 2. C. 4. D.1.
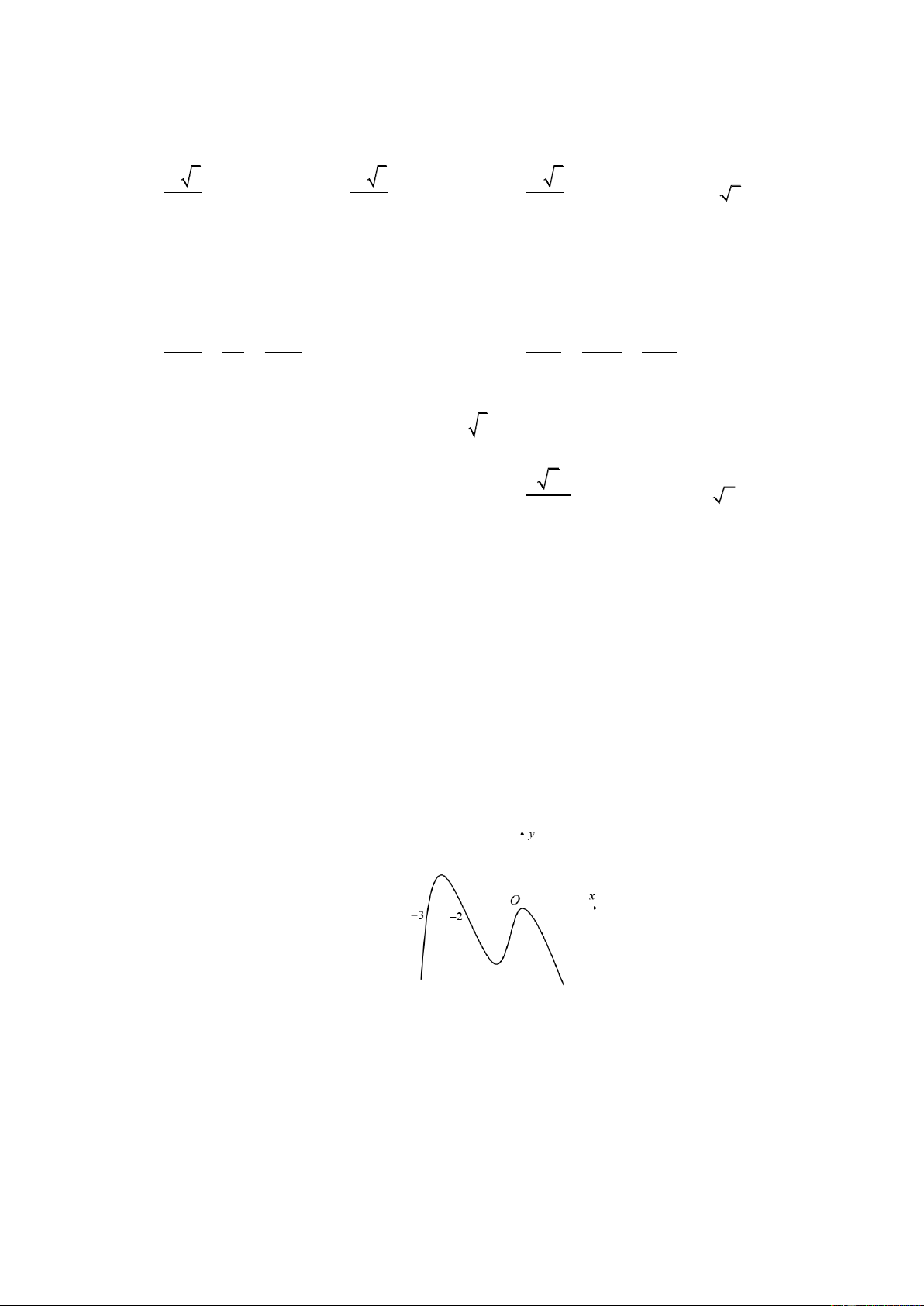
Câu 33. Cho hàm số f x xác định, có đạo hàm trên và f x có đồ thị như hình vẽ sau:
Mệnh đề nào dưới đây đúng?
A.Hàm số y f x đồng biến trên khoảng ; 2 .
B.Hàm số y f x đồng biến trên khoảng 2 ;0 .
C.Hàm số y f x nghịch biến trên khoảng 3 ; 2 .
D.Hàm số y f x nghịch biến trên khoảng 2; .
Câu 34. Cho tập hợp M 1;2;3;4;
5 . Số tập con gồm hai phần tử của tập hợp M là 2 2 A.11. B. A . C. C . 5 P . D. 2 5 Trang4
Câu 35. Cho hàm số y f x xác định và liên tục trên . Đồ thị của hàm số y f x như hình bên dưới. x
Đặt g x f x 2
x 2022. Mệnh đề nào dưới đây đúng? 2
A. g 2 g 3
g 0 . B. g 3
g 0 g 2 .
C. g 2 g 0 g 3 .
D. g 0 g 2 g 3 .
Câu 36. Cho khối chóp S.ABCD có đáy là hình thoi cạnh 2a ,
ABC 60 , cạnh bên SA vuông góc với
mặt phẳng đáy, mặt bên SCD tạo với đáy một góc 60. Thể tích khối chóp S.ABC bằng 3 3 A. 3a 3 . B. 3 2a 3 . C. a 3 . D. 3 2a . x 1 y z 2
Câu 37. Trong không gian Oxyz , cho đường thẳng :
và điểm M 2;5;3 . Mặt 2 1 2
phẳng P chứa sao cho khoảng cách từ M đến P lớn nhất có phương trình là
A. x 4 y z 3 0 .
B. x 4 y z 1 0 .
C. x 4 y z 3 0 . D. x 4 y z 1 0 .
Câu 38. Có bao nhiêu số nguyên dương a sao cho tồn tại số thực x thoả phương trình sau 3 3log x 1 x a 3 2021 x 2020 3log x 1 a 2020 A. 9 . B. 5 . C.8 . D.12 .
Câu 39. Gọi S là tập các số tự nhiên có 4 chữ số khác nhau được lập từ E 1; 2;3; 4; 5 . Chọn ngẫu
nhiên một số từ tập S. Xác suất để số được chọn là số chẵn bằng 1 3 3 2 A. . B. . C. . D. . 2 4 5 5 2
x x 1 khi x 0
Câu 40. Cho hàm số f x 2x 1 khi x 0 2 2 e Biết f x a f 2sin x ln 1 .cos d x x
với a là phân số tối giản. Giá trị của a. b bằng x b b 0 e A. 60 . B. 92 . C.174 . D.132 .
Câu 41. Cho hai số phức
z , z thỏa mãn z 1 3i 1 và z 1 i z
5 i . Giá trị nhỏ nhất của biểu 1 2 1 2 2
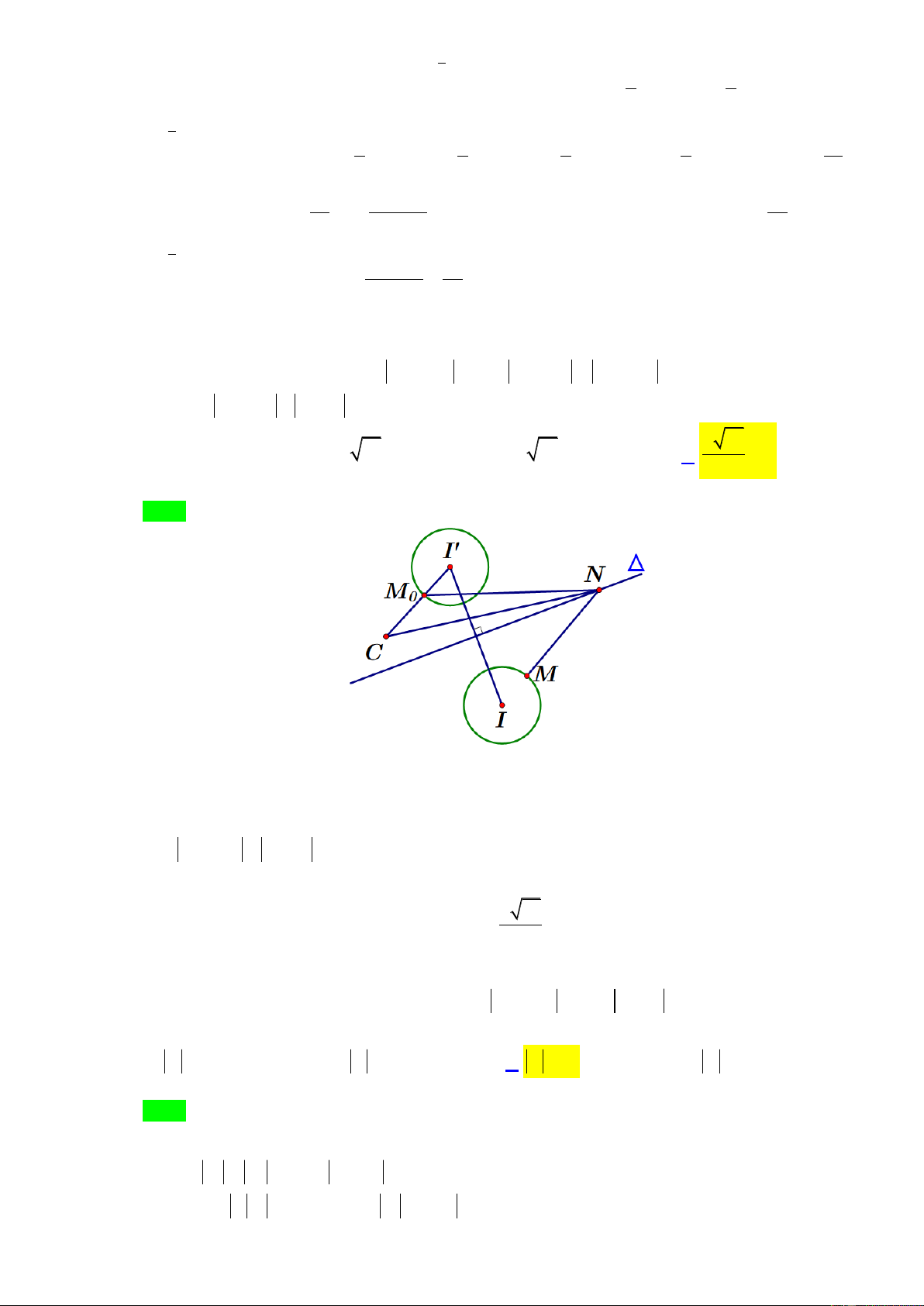
thức P z 1 i z z bằng 2 2 1 2 85 A. 3. B. 10 . 1 C. 10 . 1 D. . 1 5 Câu 42. Gọi
z , z là hai trong các số phức z thỏa mãn z 3 5i 5 và z z 6. Môđun của số phức 1 2 1 2
w z z 6 10i là 1 2 A. w 16. B. w 32. C. w 8. D. w 10. Trang5
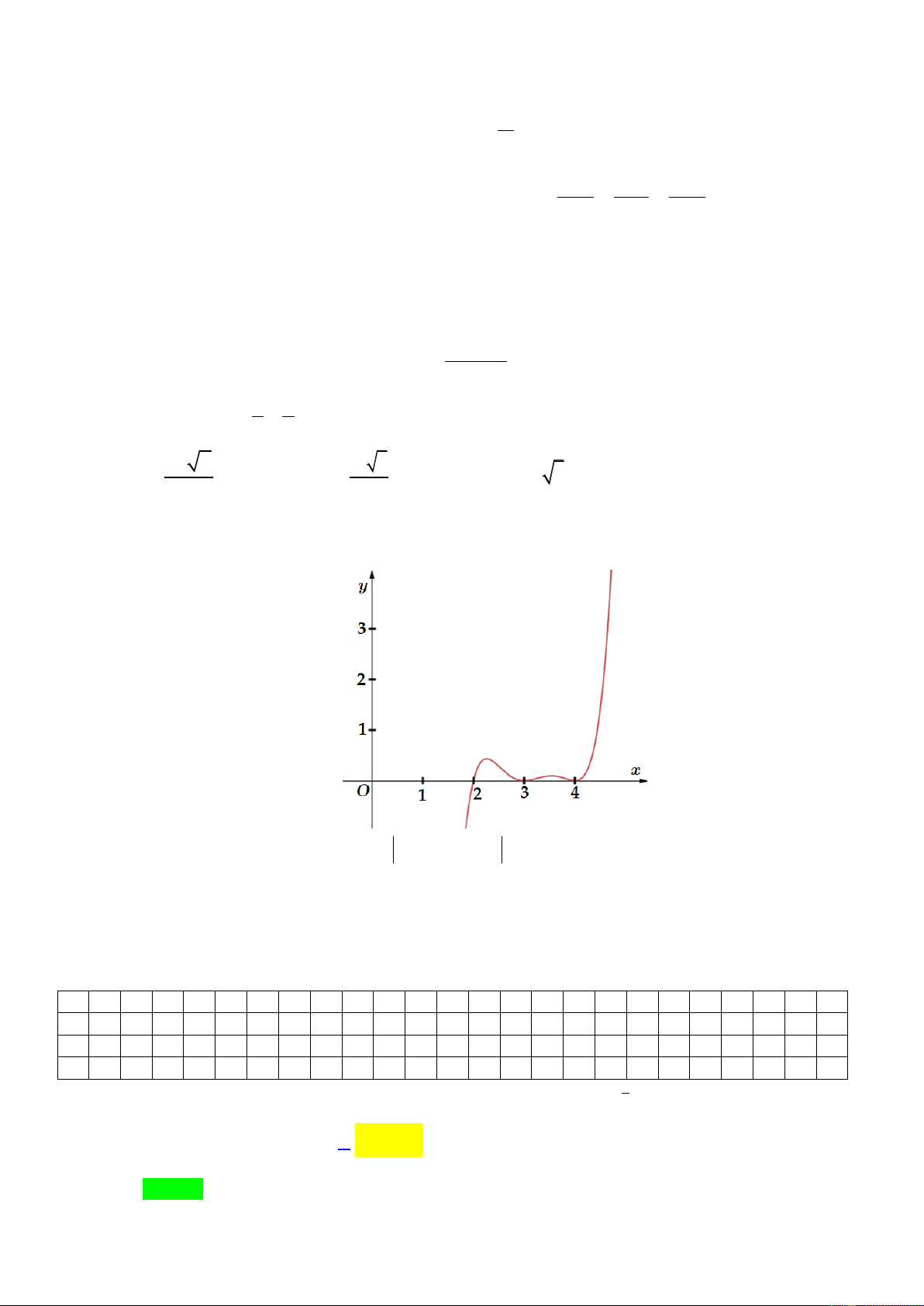
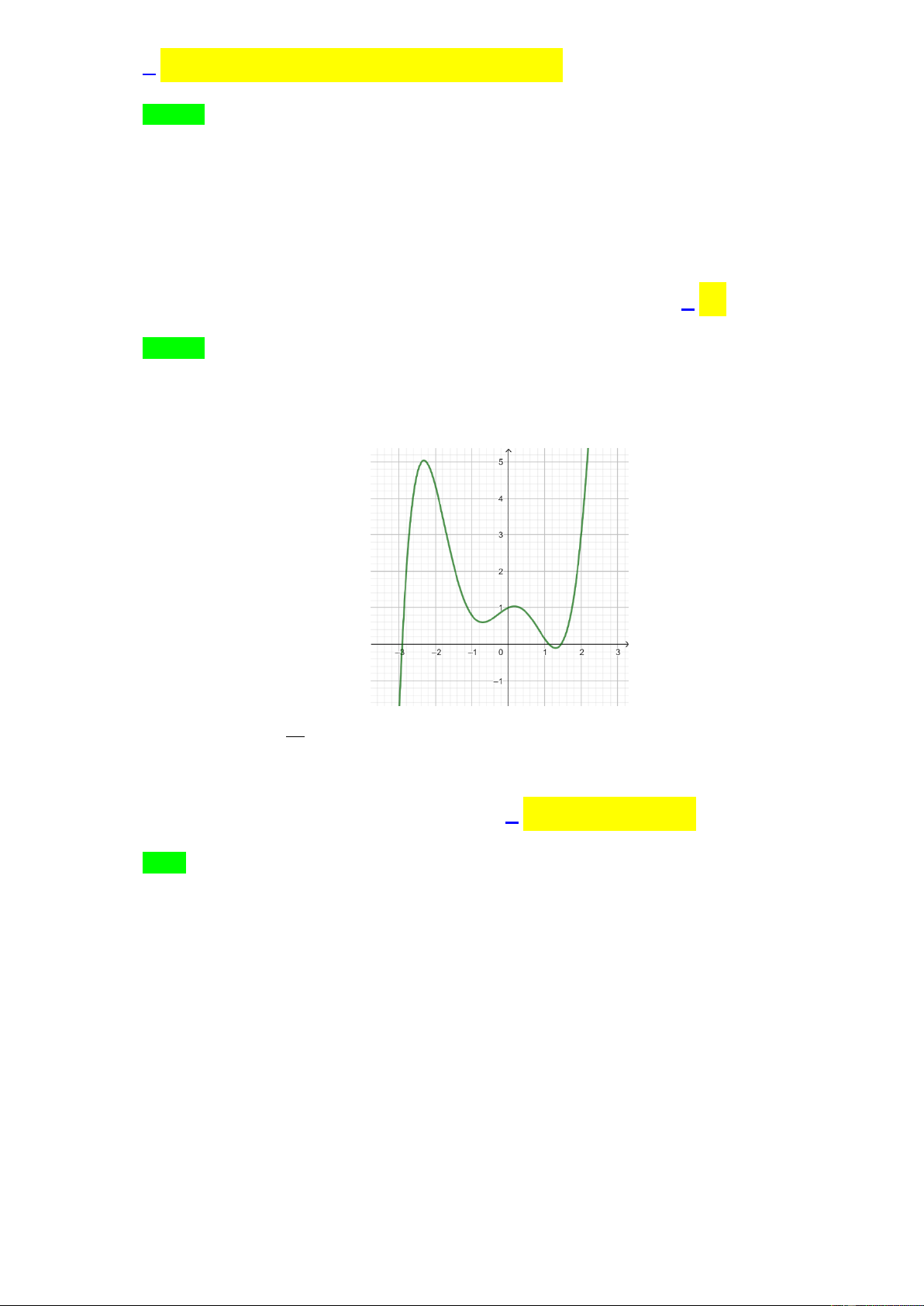
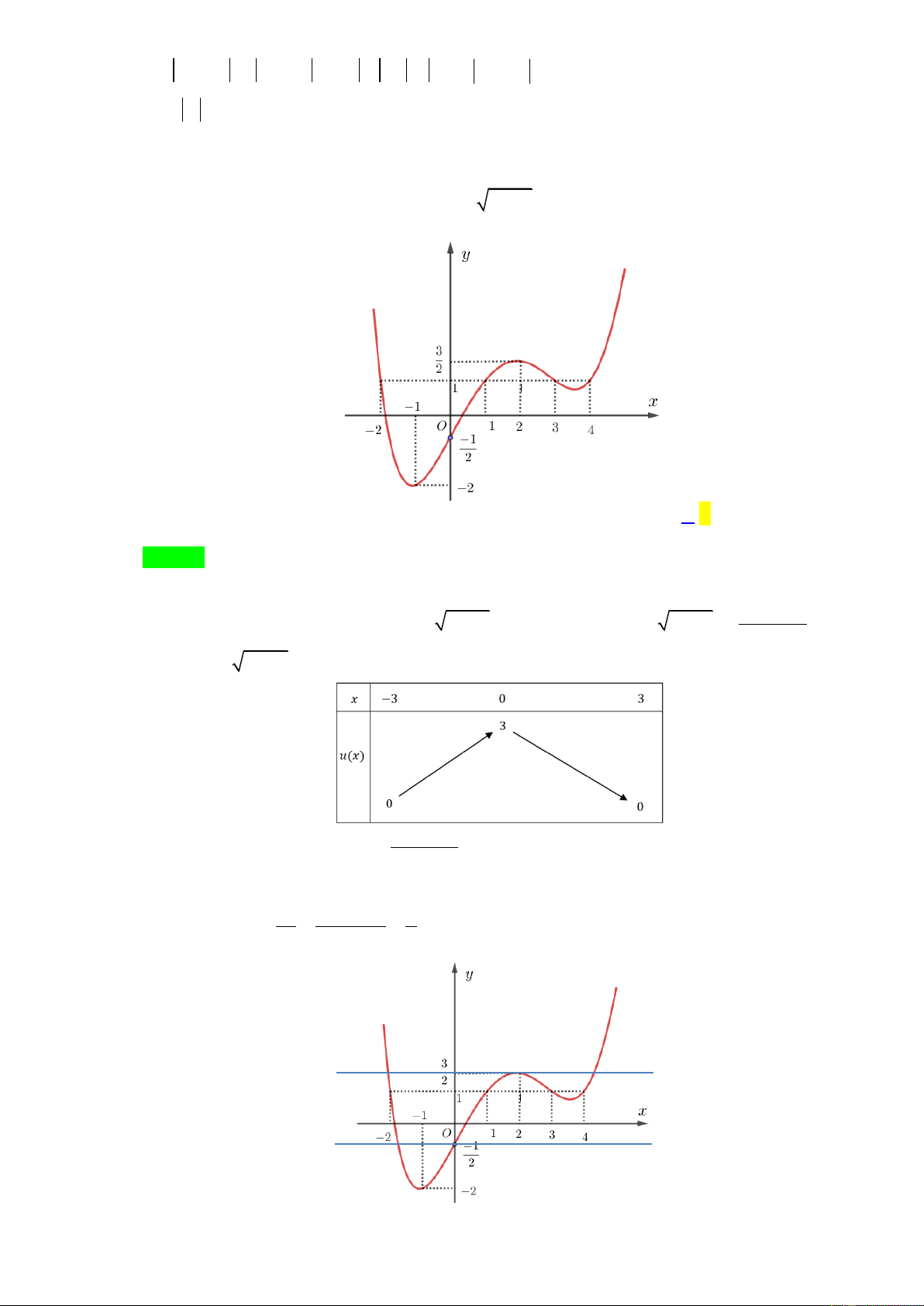
Câu 43. Cho hàm số y f x xác định và liên tục trên có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số m để phương trình f 2 2
9 x m 2022 0 có nghiệm? A. 7 . B. 8 . C. 4 . D. 5 . f x
Câu 44. Cho hàm số f x 0 và có đạo hàm liên tục trên , thỏa mãn x f x 1 và x 2 2 f ln 2 0
. Giá trị f 3 bằng 2 1 1 A. 2 4 4ln 2 ln 5 B. 2 2 4 ln 2 ln 5 C. 4ln 2 ln52 D. 4ln 2 ln52 2 4
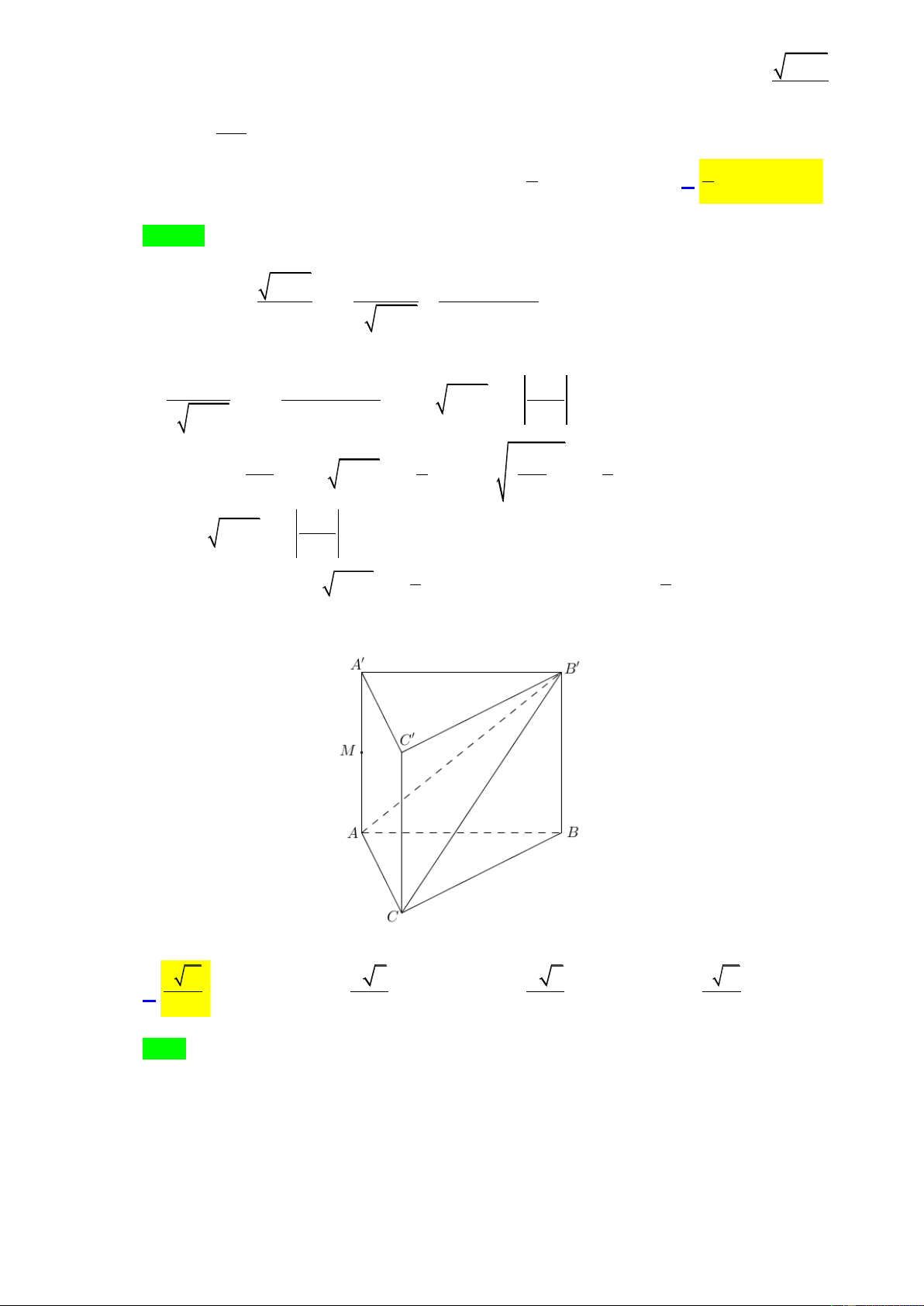
Câu 45. Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng a . Gọi M là trung điểm của AA (tham khảo hình vẽ).
Khoảngcách từ M đến mặt phẳng AB C bằng a 21 a 2 a 2 a 21 A. . B. . C. . D. . 14 4 2 7
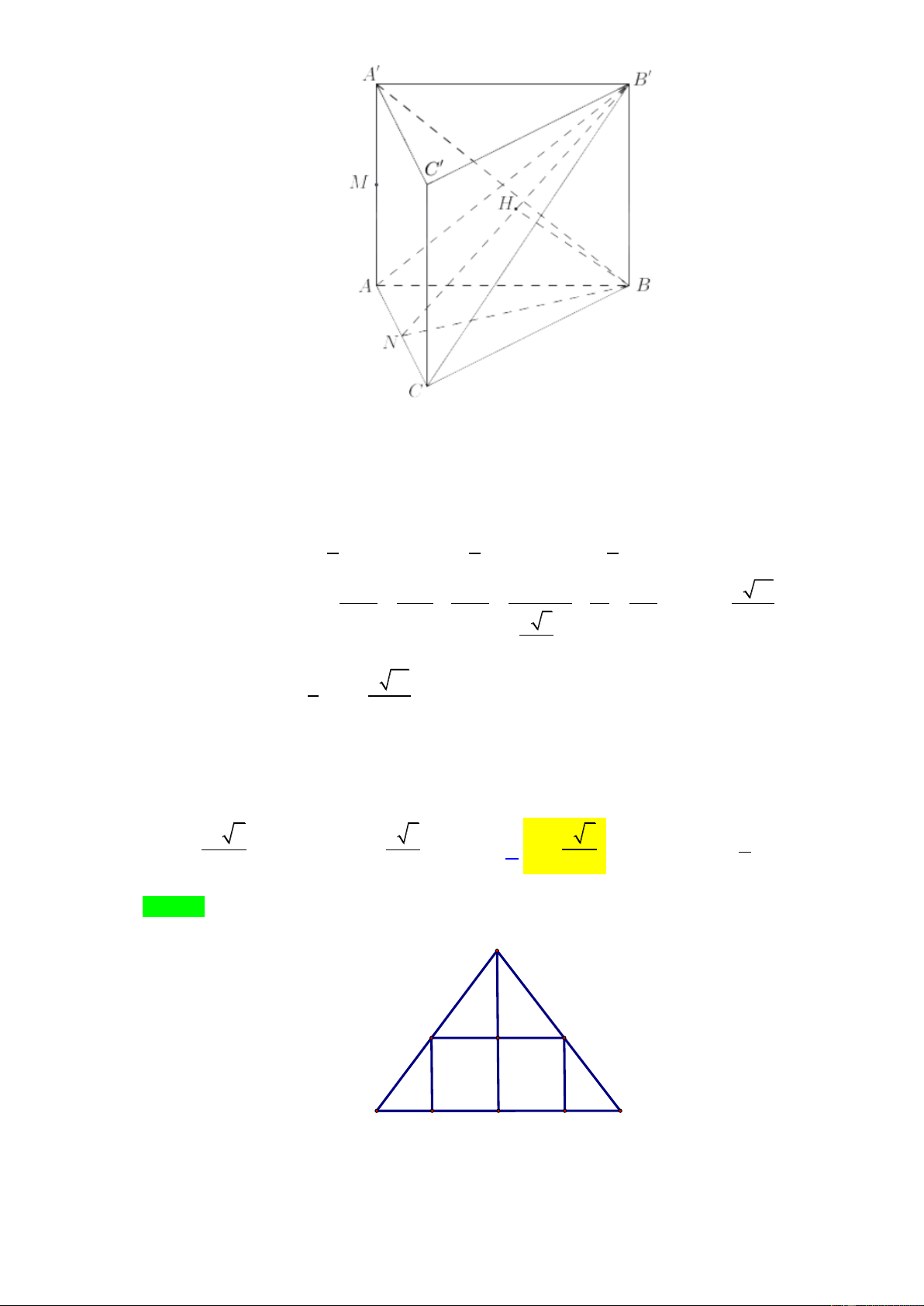
Câu 46. Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Một mặt phẳng thay đổi, vuông góc
với cắt SO , SA, SB , SC , SD lần lượt tại I , M , N, P,Q . Một hình trụ có một đáy nội tiếp tứ
giác MNPQ và một đáy nằm trên hình vuông ABCD . Khi thể tích khối trụ lớn nhất thì độ dài SI bằng 3a 2 a 2 a 2 a A. SI . B. SI . C. SI . D. SI . 2 2 3 3 x y z
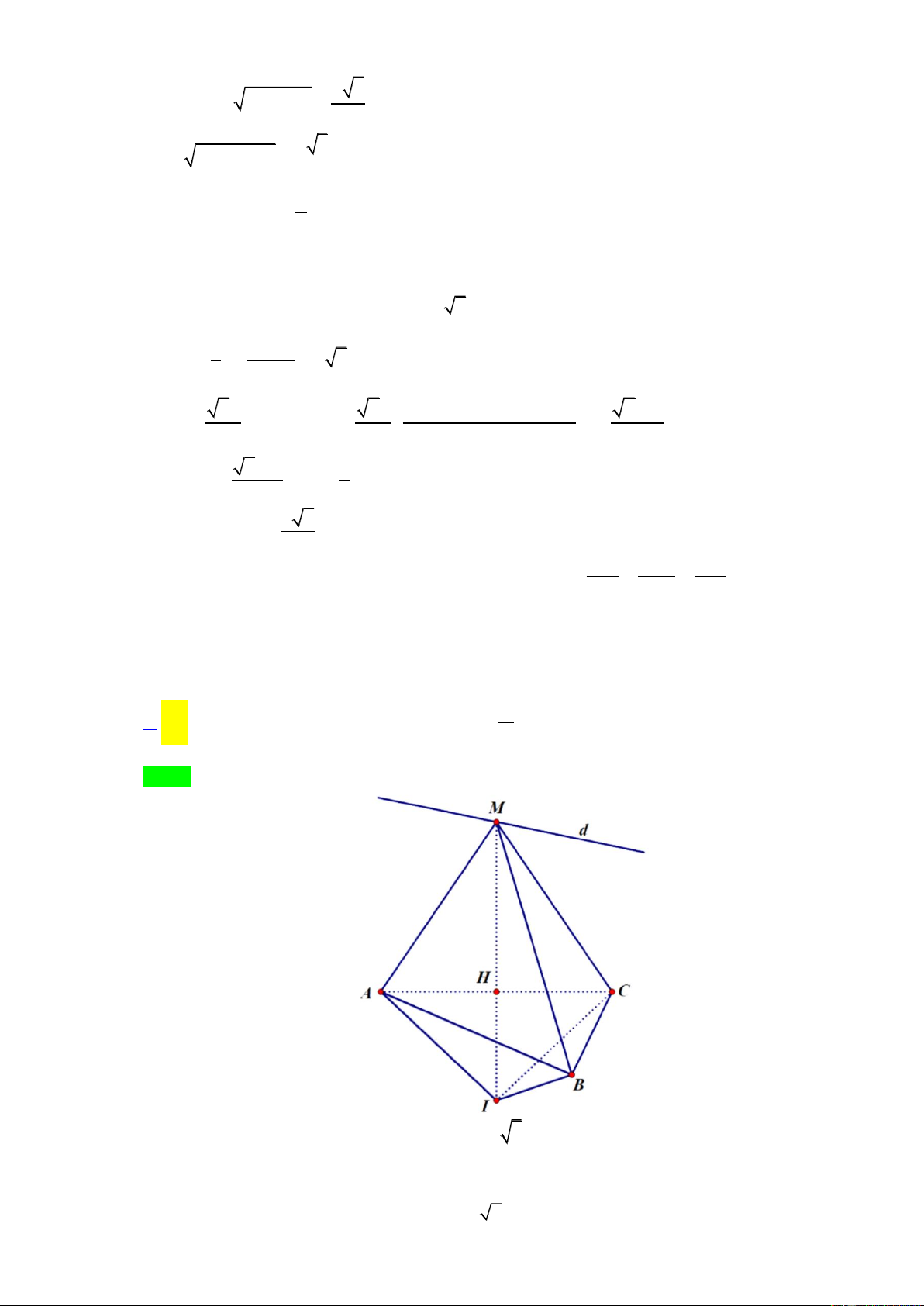
Câu 47. Trong không gian Oxyz , cho đường thẳng 1 2 1 d : và mặt cầu 1 1 1 S 2 2 2
: x y z 2x 4 y 6z 13 0 . Lấy điểm M a; ;
b c với a 0 thuộc đường thẳng d Trang6
sao cho từ M kẻ được ba tiếp tuyến MA , MB , MC đến mặt cầu S ( ,
A B, C là tiếp điểm) thỏa mãn góc AMB 60 , BMC 90 ,
CMA 120 . Tổng a b c bằng 10 A. 2 . B. 2 . C. . D.1. 3 x 2 x 3 y 1 z 4
Câu 48. Cho hai đường thẳng
d : y t t , : và mặt phẳng 1 1 1 z 2 2t
P: x y z 2 0 . Gọi d , lần lượt là hình chiếu của d, lên mặt phẳng P . Gọi M ; a ;
b c là giao điểm của hai đường thẳng d và . Giá trị của tổng a . b c bằng A. 5 . B. 3 . C. 4 . D. 6 .
x y 1
Câu 49. Cho các số dương x, y thoả mãn log
3x 2y 4. Giá trị nhỏ nhất của biểu thức 5
2x 3y 4 9
A 6x 2 y bằng x y 27 2 31 6 A. . B. . C.11 3 . D.19 . 2 4
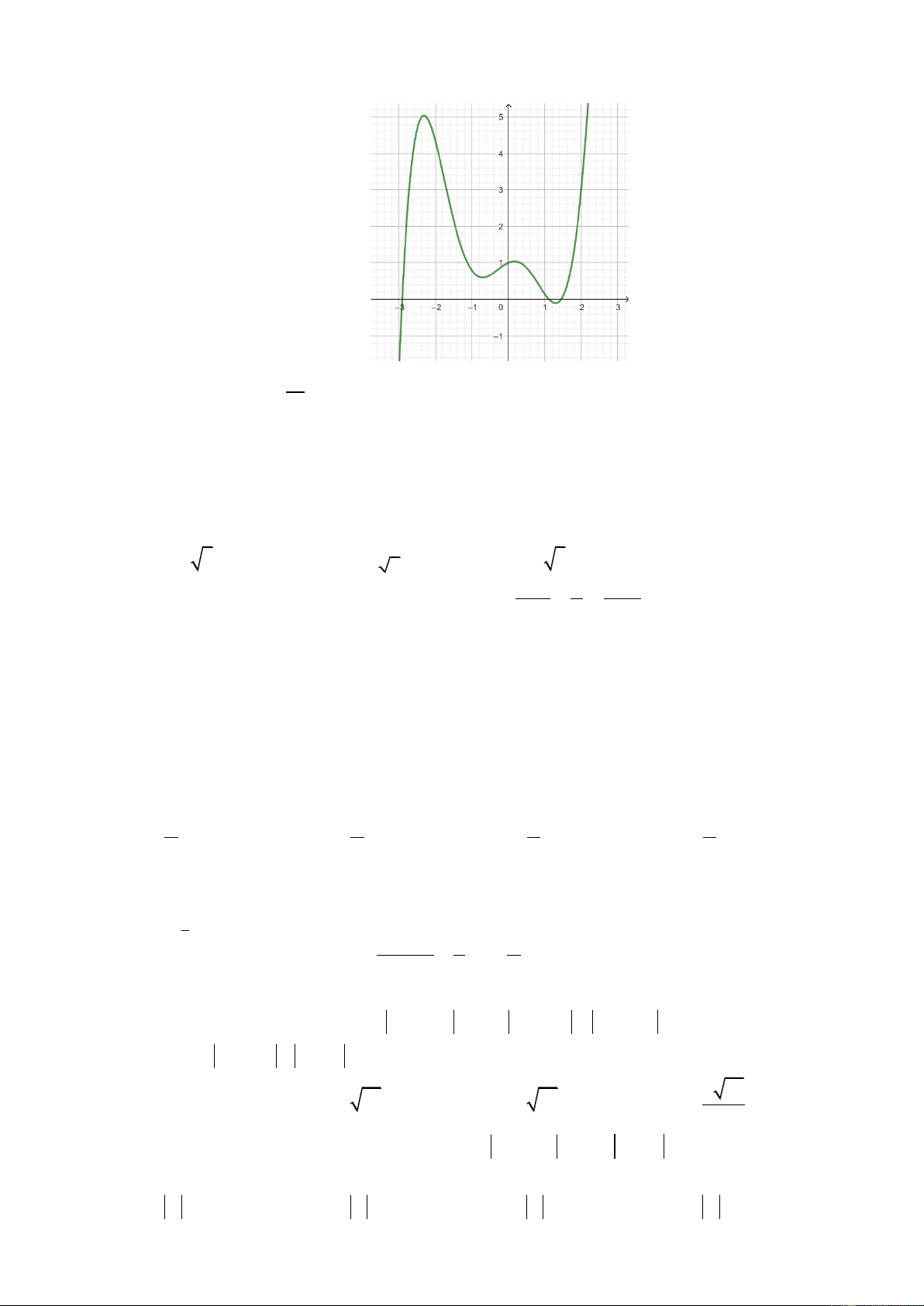
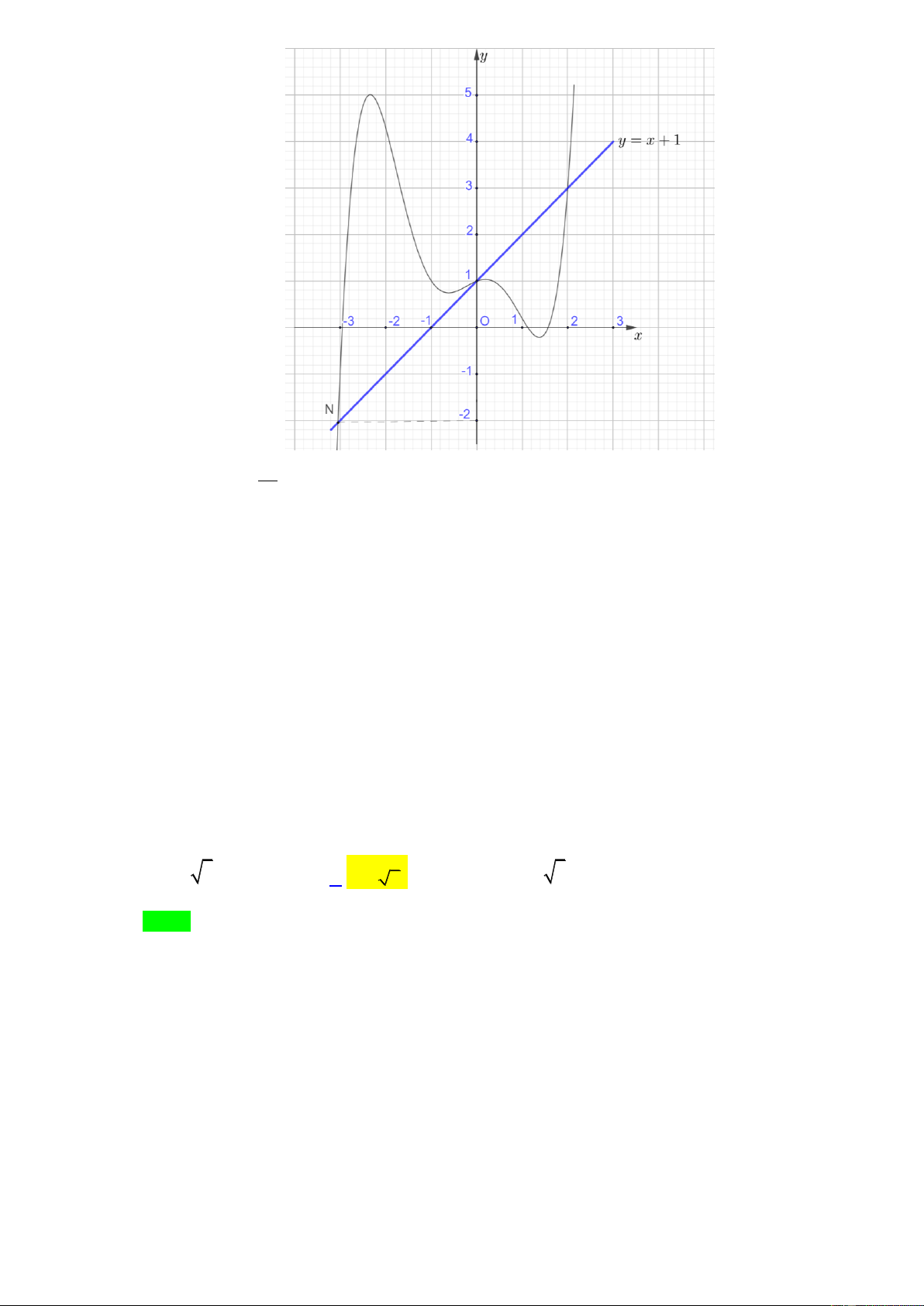
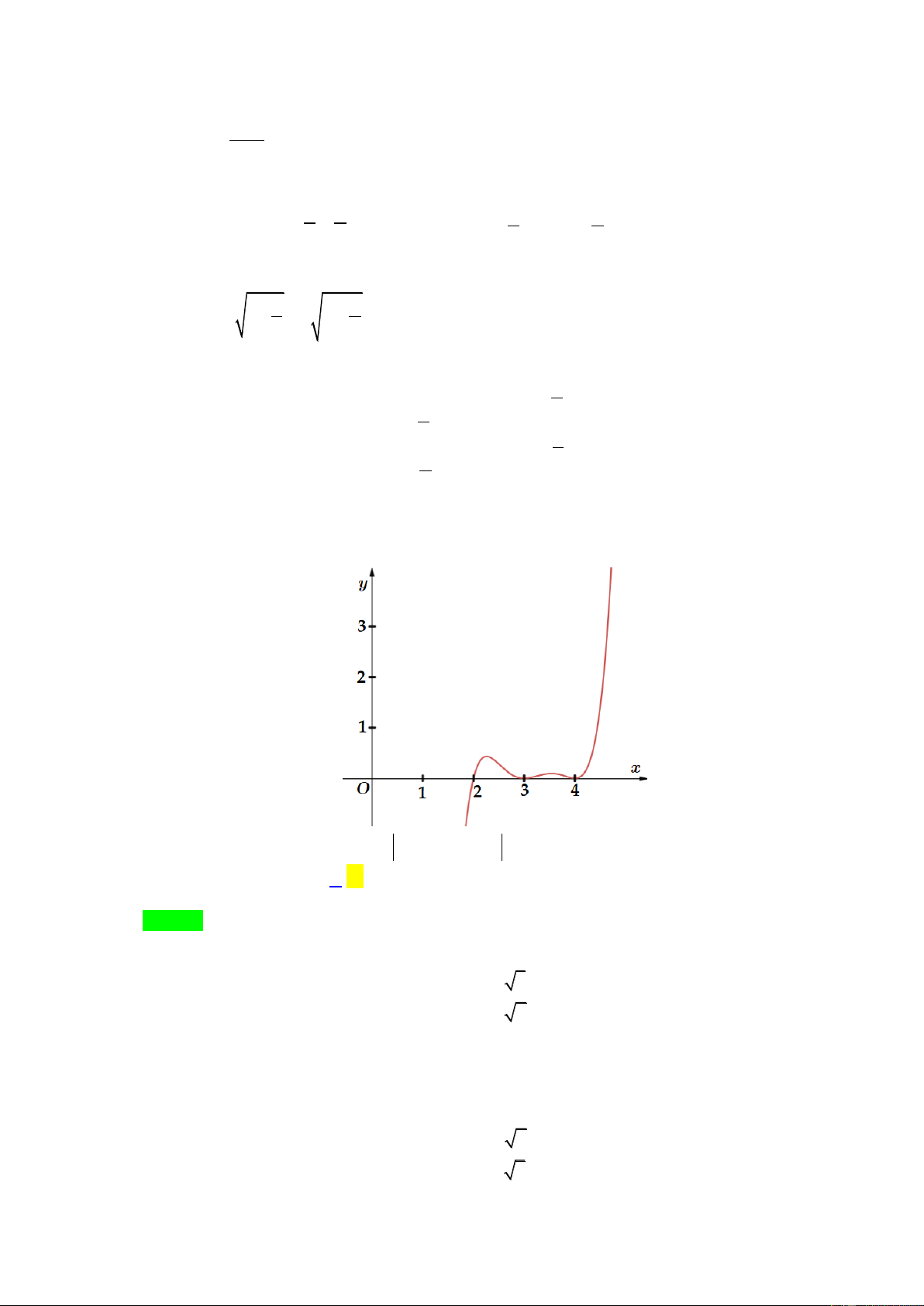
Câu 50. Cho f x là hàm đa thức bậc 6 sao cho đồ thị hàm số y f x như hình vẽ và f 2 0 , f 1 0.
Số điểm cực tiểu của hàm số y f 2
x 4x 5 là: A. 7 . B. 4 . C. 3 . D. 5 .
---------- HẾT ----------
BẢNG ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B D A B C A B A B B C A D D D C C D B A C C C B B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B A B B A D C D D D B A A D B D C D D A C A A D B Câu 1.
Cho số phức z 2 3i . Điểm biểu diễn số phức w 2z 1 i z trên mặt phẳng phức là
A. N 1;3 .
B. P 3; 1 . C. Q 3 ; 1 . D. M 3; 1 . Lời giải Chọn B Trang7
Ta có w 2z 1 i z 22 3i 1 i2 3i 3 i . Suy ra điểm biểu diễn số phức
w 2z 1 i z trên mặt phẳng phức là P3; 1 . Câu 2.
Trong không gian Oxyz , cho ba điểm A2; 1;5, B 5; 5;7 , M ; x y ; 1 . Khi , A B, M thẳng
hàng thì giá trị của x , y là
A. x 4; y 7 .
B. x 4; y 7 .
C. x 4; y 7 .
D. x 4; y 7 Lời giải Chọn D
Ta có AB 3; 4; 2, AM x 2; y 1; 4 . ,
A B, M thẳng hàng khí AM k.AB
x 2 3k
x 3k 2 x 4 y 1 4
k y 4k 1 y 7 . 4 2k 2 k 4 k 2 Câu 3.
Trong không gian Oxyz , mặt cầu S 2 2 2
: x y z 2x 4y 1 0 có tâm là
A. I 1; 2;0 . B. I 2 ;4;0 . C. I 1 ;2;0. D. I 1 ;2; 1 . Lời giải Chọn A
Ta có tâm I 1; 2;0 . Câu 4.
Tập nghiệm của bất phương trình log x + 1 < 3 là 2 ( ) A. S = (- 1; ) 8 .
B. S = (- 1;7). C. S = (- ¥ ) ;8 .
D. S = (- ¥ ;7). Lời giải ChọnB. íï x > - 1 log x + 1 < 3 ï Û ì Û - 1< x < 7. 2 ( ) ï x + 1< 8 ïî
Vậy bất phương trình có tập nghiệm S = (- 1;7). Câu 5.
Cho số phức z thỏa mãn (1+ 2i)z = 3- 4i . Phần ảo của số phức z bằng A. - 4 . B. 2 . C. - 2 . D. 4 . Lời giải ChọnC.
(1+ 2i)z = 3- 4i 3- 4i Û z = = - 1- 2i . 1+ 2i
Vậy số phức z có phần ảo bằng - 2 . 1 Câu 6.
Tập xác định của hàm số y = ( 2 x - )5 9 1 là æ - 1ö 1 æ ö íï ü = ç ÷ - ¥ Èç ÷ 1 ï ï A. D ; ç ÷ ;+ ¥ ç ÷ ç D = ¡ \ ì ± ý è . 3 ÷ ø è3 ç ÷ø. B. ïî 3ï ï ïþ æ 1ù 1 é ö æ- ö = ç ÷ 1 1 ç ÷ C. D - ¥ ; úÈ ê ;+ ¥ ç ÷ ç D = ; ç ÷ è . D. 3ú 3 ÷ ê ø û ë çè 3 3÷ø. Lời giải Chọn A. é - 1 x ê < ê æ - 1ö 1 æ ö Û Î ç ÷ - ¥ Èç ÷ Điều kiện: 2 3 9x - 1> 0 Û ê x ; ç ÷ ;+ ¥ ç ÷ ê ç ÷ è ø ç ÷ 1 3 è3 ø. x ê > êë 3 Trang8 æ - 1ö 1 æ ö = ç ÷ - ¥ Èç ÷
Vậy tập xác định của hàm số D ; ç ÷ ;+ ¥ ç ÷ çè 3 ÷ ø è3 ç ÷ø. Câu 7.
Cho hình chóp S.ABC đáy là tam giác đều cạnh a . Cạnh bên SC vuông góc với mặt phẳng
ABC, SC a. Thể tích khối chóp S.ABCbằng 3 a 3 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 3 12 12 9 Lời giải ChọnB. 1 1 a 3 a 3 Ta có V .S . C dt ABC a . S ABC 2 3 . . 3 3 4 12 1 1 1 Câu 8. Nếu tích phân
f (x)dx = - 2 ò và
g (x)dx = 7 ò thì 2
é f (x)- 3g(x) d ù x ò ë û bằng 0 0 0 A. 25. B. 12. C.17. D. 25. Lời giải Chọn A. 1 1 1 Ta có: 2 f
x3gxdx 2 f
xdx3 g
xdx 2. 2 3.7 2 5. 0 0 0 Câu 9.
Trong không gian Oxyz , mặt phẳng P : x y z 3 0 đi qua điểm nào dưới đây?
A. M 1;1; 1 . B. N 1 ; 1 ;1 . C. N 1;1 ;1 . D. Q 1 ;1; 1 . Lời giải ChọnB.
Thay tọa độ điểm N 1 ; 1
;1 vào phương trình mặt phẳng P ta được: 1
113 0 0 0 (đúng)
N P .
Các điểm còn lại thay tọa độ vào phương trình P không thỏa mãn.
Câu 10. Cho hàm số f x có bảng xét dấu của đạo hàm như sau Trang9
Số điểm cực trị của hàm số đã cho là A. 3 . B. 2 . C.1. D. 5 . Lời giải Chọn B
Từ bảng biến thiên ta thấy hàm số có 2 điểm cực trị.
Câu 11. Cho khối nón có chiều cao h và bán kính đáy bằng r . Thể tích của khối nón đã cho bằng 1 4 A. 2 rh . B. 2 r h C. 2 r h . D. 2 r h . 3 3 Lời giải Chọn C
Thể tích của khối nón đã cho bằng: 1 2 V r h . 3
Câu 12. Hàm số nào dưới đây có đồ thị như hình vẽ bên? 2x 1 2x 1 2x 1 A. y . B. y C. . D. y . x 1 x 1 x 1 Lời giải Chọn C
Từ đồ thị ta thấy:
+) Tiệm cận đứng: x 1 loạiD.
+) Tiệm cận ngang: y 2 loạiC.
+) x 0 y 1 loại đáp ánB. Vậy chọnA.
Câu 13. Tích tất cả các nghiệm của phương trình 2
log x 2log x 7 0 là 3 3 A. 2 . B. 7 . C.1. D. 9 . Lời giải Chọn D.
Điều kiện x 0 . 2
Có log x 2 log x 7 0 log x 1 2 2 hoặc log x 1 2 2 3 3 3 1 3 2
log x log x 1 2 2 1 2 2 3 1 3 2
log x .x 2
2 x .x 3 9 . 3 1 2 1 2
Câu 14. Họ nguyên hàm của hàm số f x 3x sin x là A. 2 3x f x dx
cos x C . B. f x 2
dx 3x cos x C . 2 x C. f
xdx 3cosxC . D. f x 2 3 dx
cos x C . 2 Lời giải Chọn D. Trang10 x
Họ nguyên hàm của hàm số f x 3x sin x là f x 2 3 dx
cos x C . 2
Câu 15. Môđun của số phức z 2 3i bằng A. 5 . B. 5 . C. 7 . D. 7 . Lời giải ChọnD. Có z i 2 2 2 3 2 3 7 . 5 a
Câu 16. Cho a, b là hai số thực dương và a khác 1 thỏa mãn log
2 . Giá trị của biểu thức 3 a 4 b bằng 1 1 A. 4 . B. . C. 4 . D. . 4 4 Lời giải ChọnC. 5 5 a 1 a 1 1 1 Ta có: 5 4 log log log a log b 5 .log b 2 . 3 4 a 4 a a b 3 b 3 3 4 a a 1 1
5 log b 6 log b 1 log b 4 4 a 4 a a x
Câu 17. Tiệm cận ngang của đồ thị hàm số 3 2 y
là đường thẳng có phương trình x 2 2 3 A. y 2 . B. y . C. y 3 . D. y . 3 2 Lời giải ChọnC. 2 3 3x 2 Ta có: lim lim x 3. x x 2 x 2 1 x 2 3 3x 2 lim lim x 3. x x 2 x 2 1 x
Nên y 3 là tiệm cận ngang của đồ thị hàm số. Câu 18. Cho hàm số 4 2
y ax bx cx d có đồ thị như hình dưới. Mệnh đề nào đúng?
A. a 0;b 0; c 0; d 0 .
B. a 0;b 0; c 0; d 0 .
C. a 0;b 0; c 0; d 0 .
D. a 0;b 0; c 0; d 0 . Lời giải Trang11 Chọn D.
Đồ thị hàm số nhận
Oy làm trục đối xứng nên hàm số 4 2 y ax bx
cx d là hàm số chẵn. suy ra c 0 .
Dựa vào đồ thị ta thấy: lim y a 0 . x
Hàm số có 3 cực trị nên ab 0 b 0.
Đồ thị hàm số cắt trục Oy tại điểm có hoành độ dương nên d 0 .
Vậy a 0;b 0;c 0; d 0 .
Câu 19. Cho hàm số y f x liên tục trên và có đồ thị là đường cong như hình vẽ bên dưới
Số nghiệm của phương trình f x 2 0 trên đoạn 2 ;3 là A. 3 . B. 2 . C. 4 . D.1. Lời giải ChọnB. x Ta xét phương trình
f x f x 2 2;3 2 0 2 x 2 2 ;3
Vậy phương trình f x 2 0 có hai nghiệm trên đoạn 2 ;3
Câu 20. Giá trị nhỏ nhất của hàm số y 3cos 2x 4 sin x là: 11 A. 7 . B. . C. 5 . D.1. 3 Lời giải ChọnA. Ta có hàm số Đặt 2 t sinx; t 1 ;1 y 6
t 4t 3;t 1 ;1 1 Có y' 1
2t 4 0 t 3 Xét BBT: Trang12
Giá trị nhỏ nhất của hàm số y 3cos 2x 4sin x là 7
Câu 21. Cho hình nón N đỉnh S đáy là đường tròn C ; O
R , đường cao SO 40cm . Người ta cắt 1
hình nón bằng mặt phẳng vuông góc với trục để đường hình nón nhỏ N có đỉnh S và đáy là 2 VN 1
đường tròn C'O'; '
R .Biết rằng tỉ số thể tích 1
. Độ dài đường cao của hình nón N V 8 2 N2 là: A. 5cm . B.10cm. C. 20cm. D. 49cm. Lời giải Chọn C. R S O Ta có S
O' A và S
OB đồng dạng nên ta có R SO VN 1 R .SO 1 SO 3 2 1 SO 1 1 1 S O SO 20cm 2 V 8 R .S O 8 S O 8 S O N 2 2 2
Câu 22. Cho hàm số f x liên tục trên 3;7 , thoả mãn f x f 10 x với mọi x 3;7 và 7 7 f
xdx 4. Tích phân xf xdx bằng 3 3 A. 80 . B. 60 . C. 20 . D. 40 . Lời giải ChọnC. 7 Xét I xf xdx . 3
Đặt x 10 t dx d t .
Đổi cận x 3 t 7; x 7 t 3 . 7 7 7 7
Ta có I 10 t f 10 tdt 10 t f tdt 10 f
tdt tf
tdt 10.4 I . 3 3 3 3
Suy ra 2I 40 I 20 .
Câu 23. Cho cấp số cộng u với u 10,u 13. Giá trị của u là n 1 2 4 A. u 18 . B. u 16 . C. u 19 . D. u 20 . 4 4 4 4 Lời giải ChọnC.
Ta có d u u 3 u u 3d 10 3.3 19 2 1 4 1 .
Câu 24. Cho số phức z có z 1
2 và w 1 3i z 2 . Tập hợp các điểm biểu diễn số phức w là
đường tròn , tâm và bán kính của đường tròn đó là Trang13 A. I 3 ; 3, R 4 .
B. I 3; 3, R 4 .
C. I 3; 3, R 2 .
D. I 3; 3, R 4 . Lời giải ChọnB.
w 1 3i z 2 1 3i z w 2 .
Ta có z 1 2 1 3i z 1 3i 2 1 3i w 2 1 3i 4 w 3 3i 4 (1)
Đặt w x yi với x, y . Khi đó ta được: x yi i
x y 2 x y 2 2 2 3 3 4 3 3 4 3 3 16
Vậy tập hợp các điểm biểu diễn số phức w 1 3iz 2 là một đường tròn có tâm
I 3; 3 và bán kính R 4 .
Câu 25. Cho log 5 m log 5 n . Khi đó log 5 m n 2 , 3 6 tính theo , là mn 1 A. 2 2 m n B. C.
D. m n m n m n Lời giải Chọn B 1 1 1 mn Ta có: log 5 . 6 log 6 log 2 log 3 1 1 m n 5 5 5 log 5 log 3 2 2
Câu 26. Trong không gian Oxyz , cho mặt phẳng P : x y z 1 0 và đường thẳng x 1 y z d :
. Gọi d là hình chiếu vuông góc của d lên mặt phẳng P . Đường thẳng 1 1 2 1 3 1
d nằm trên P tạo với d , d các góc bằng nhau, d có vectơ chỉ phương u a ; b ; c . Giá trị 2 1 1 2
biểu thức 3a b bằng c 11 11 13 A. B. C. 4 D. 3 3 3 Lời giải Chọn B
Đường thẳng d có vectơ chỉ phương là u 2;1;3 , mặt phẳng P có vec tơ pháp tuyến là 1 1 n 1; 1;1 . 1
Tọa độ giao điểm C của d và P là: C 1;0;0. 1
Vectơ chỉ phương của đường thẳng d là u
u , n , n 2;7;5 2 1 1 1 . 1
d nằm trên P tạo với d , d các góc bằng nhau nên ta có 2 1 1 . u n 0
a c b 1 u.u u.u
2a b 3c
2a 7b 5c . 1 2 u . u u . u 14 78 1 2 4
a c b a c
a c b 3 a b 3a 4c
9a 12c Vậy 3 11 . 3
a 4c 0 1 c 3 14 78 b c 3 Trang14
Câu 27. Cho hình hộp đứng ABC . D A B C D
có đáy là hình vuông cạnh a , góc giữa mặt phẳng D AB
và mặt phẳng ABCDlà 30 . Thể tích khối hộp ABC . D A B C D bằng 3 a 3 3 a 3 3 a 3 A. B. C. D. 3 a 3 3 18 9 Lời giải Chọn A Góc giữa mặt phẳng D AB
và mặt phẳng ABCDlà góc DAD nên DAD 30. a
Độ dài đường cao là: DD A . D tan 30 . 3 3 Thể tích khối hộp a a 3 ABC . D A B C D là: 2 V .a . 3 3
Câu 28. Trong không gian Oxyz , phương trình đường thẳng d đi qua A1; 2 ;1 và vuông góc với
P: x2y z 1 0 là x 1 y 2 z 1 x 2 y z 2 A. . B. . 1 2 1 2 4 2 x 2 y z 2 x 1 y 2 z 1 C. . D. . 1 2 1 2 2 1 Lời giải ChọnB.
Vì đường thẳng d vuông góc với mặt phẳng P nên vectơ chỉ phương của đường thẳng d là u d nP
1; 2; 1 hay u d 2; 4;2 . x 1 t
Phương trình tham số của đường thẳng d là y 2 2t , t . z 1t
Chọn t 1 ta được điểm B2;0;2d .
Vậy phương trình chính tắc của đường thẳng x 2 y z 2
d đi qua B 2;0; 2 là . 2 4 2
Câu 29. Cho hình trụ có bán kính bằng 3a . Cắt hình trụ bởi mặt phẳng P song song với trục của hình
trụ và cách trục của hình trụ một khoảng a 5 ta được một thiết diện hình vuông. Thể tích của khối trụ đã cho bằng 2 2 3 A. 3 12 a . B. 3 36 a . C. a . D. 3 2 2 a . 3 Lời giải ChọnB. Trang15
Xét tam giác OAB vuông tại A có AB
OB OA AB
a a 2 2 2 2 3 5 2a .
Suy ra: BC 2AB 4a .
Do mặt phẳng P cắt hình trụ ta được thiết diện hình vuông nên bốn cạnh bằng nhau.
Suy ra chiều cao của hình trụ là h BC 4a .
Thể tích của khối trụ đã cho là V R h a2 2 3 3
4a 36a . x
Câu 30. Một nguyên hàm của hàm số f x 3 1 2 e 2x là 3x 1 3 e 2x 3x 1 3 e x 3x 1 e 3x 1 e 3 3 A. . B. . C. 2x . D. x . 3 3 3 3 Lời giải Chọn A. Ta có: x x
f x dx e x 2x 3 1 3 1 x 2 e 2 3 1 2 3 1 3 dx e x C C . 3 3 3 3x 1 3 e 2x
Vậy một nguyên hàm của hàm số f x là . 3
Câu 31. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD , SA a , đáy ABCD là hình
thang vuông tại A và B với AB BC a , AD 2a . Góc giữa hai mặt phẳng SBC và
SCD bằng A. 30 . B.150 . C. 90 . D. 60 . Lời giải Chọn D Trang16
Có SA ABCD , đáy ABCD là hình thang vuông tại A và B nên SA BC
BC SAB . Trong S
AB dựng đường cao AH SB AH SBC . AB BC Ta có
AC a 2 ; AD a 5 ; D C
a 2 ; SC a 3 . Do đó D SC vuông tại C . SC D C Có D
C SAC . Trong S
AC dựng đường cao AK SC AK SAC SA D C
Từ đó góc giữa hai mặt phẳng SBC và SCD bằng góc giữa AH và AK bằng HAK
AH SBC AH HK . 1 1 1 a 1 1 1 a 2 Có AH ; AK 2 2 2 AH SA AB 2 2 2 2 AK SA AC 3 AH 3
Tam giác vuông AHK có cosHAK HAK 60 AK 2
Câu 32. Đồ thị của hàm số 3 2 2
y x 2mx m x n có điểm cực tiểu là I 1; 3. Khi đó m n bằng A. 3. B. 2. C. 4. D.1. Lời giải Chọn C 3 2 2 2 2
y x 2mx m x n y 3x 4mx m . x m y 0 m 0 m x 3 m m Xét m 0
m . Vì đạo hàm của hàm số có hệ số bằng 3 0 nên x là điểm cực tiểu 3 3 của hàm số m
1 m 3 ( loại) 3 m Xét m 0
m . Vì đạo hàm của hàm số có hệ số bằng 3 0 nên x m là điểm cực tiểu 3
của hàm số m 1 ( thỏa mãn). Đồ thị của hàm số 3 2 2
y x 2mx m x n có điểm cực tiểu là I 1; 3 nên ta được: y 1 0 m 1 m 1 . y m n 4 2 1 3 1
2m m n 3 n 3
Câu 33. Cho hàm số f x xác định, có đạo hàm trên và f x có đồ thị như hình vẽ sau:
Mệnh đề nào dưới đây đúng?
A.Hàm số y f x đồng biến trên khoảng ; 2 .
B. Hàm số y f x đồng biến trên khoảng 2 ;0 .
C. Hàm số y f x nghịch biến trên khoảng 3 ; 2 . Trang17
D.Hàm số y f x nghịch biến trên khoảng 2; . Lời giải Chọn D
Dựa vào đồ thị, ta có:
f x 0 trên khoảng 3 ; 2
. Suy ra y f x đồng biến trên khoảng 3 ; 2 .
f x 0 trên các khoảng ; 3 và 2;
. Suy ra y f x nghịch biến trên các khoảng ; 3 và 2; .
Câu 34. Cho tập hợp M 1;2;3;4;
5 . Số tập con gồm hai phần tử của tập hợp M là 2 2 A.11. B. A . C. C . 5 P . D. 2 5 Lời giải Chọn D
Số tập con gồm 2 phần tử của tập hợp gồm 5 phần tử là 2 C . 5
Câu 35. Cho hàm số y f x xác định và liên tục trên . Đồ thị của hàm số y f x như hình bên dưới. x
Đặt g x f x 2
x 2022. Mệnh đề nào dưới đây đúng? 2
A. g 2 g 3
g 0 . B. g 3
g 0 g 2 .
C. g 2 g 0 g 3 .
D. g 0 g 2 g 3 . Lời giải ChọnD. Trang18 2x g x f x
x 2022 gx f x x 1 . 2 x 3
g x 0 f x x 1 x 0 x 2 0 0 Xét g
xdx f
xx 1 dx 0
g 0 g 3
0 g 0 g 3 . 3 3 2 2 Tương tự, xét g
xdx f
xx 1 dx 0
g 2 g 0 0 g 2 g 0 . 0 0 2 0 2 Xét g
xdx f
xx 1 dx f
xx 1 dx 0 3 3 0
g 2 g 3
0 g 2 g 3
. Vậy ta có g 0 g 2 g 3 .
Câu 36. Cho khối chóp S.ABCD có đáy là hình thoi cạnh 2a ,
ABC 60 , cạnh bên SA vuông góc với
mặt phẳng đáy, mặt bên SCD tạo với đáy một góc 60. Thể tích khối chóp S.ABC bằng 3 3 A. 3a 3 . B. 3 2a 3 . C. a 3 . D. 3 2a . Lời giải Chọn B. Trang19 S A D 60° M N 60° B C
Gọi M , N lần lượt là trung điểm của AB,CD . Khi đó, tứ giác AMCN là hình chữ nhật. C D AN Ta có:
CD SN SCD ABCD SN AN , , SNA 60. C D SA 3
Xét tam giác có AB BC, ABC 60 tam giác ABC đều MC 2a a 3 . 2
Do đó, AN a 3 SA AN.tan 60 3 . a 3 Lại có, S 2S 2. a a . ABCD A BC 2 2 2 . 2 . 3 4 Vậy 1 1 2 3 V S .SA .2a 3.3a 2a 3. S . ABCD 3 ABCD 3 x 1 y z 2
Câu 37. Trong không gian Oxyz , cho đường thẳng :
và điểm M 2;5;3 . Mặt 2 1 2
phẳng P chứa sao cho khoảng cách từ M đến P lớn nhất có phương trình là
A. x 4 y z 3 0 .
B. x 4 y z 1 0 .
C. x 4 y z 3 0 . D. x 4 y z 1 0 . Lời giải ChọnA.
Hạ MK P, KH MH . Khi đó: MK MH nên d M,P MH max
Giả sử H 1 2t;t;2 2t MH 2t 1;t 5;2t 1 do : MH u
2t 1.2 t 5 2t 1.2 0 t 1 MH 1; 4 ;
1 P : x 1 4 y 1 z 2 0
P : x 4 y z 3 0 Trang20
Câu 38. Có bao nhiêu số nguyên dương a sao cho tồn tại số thực x thoả phương trình sau 3 3log x 1 x a 3 2021 x 2020 3log x 1 a 2020 A. 9 . B. 5 . C.8 . D.12 . Lời giải ChọnA.
Điều kiện: x 1 0 x 1 Đặt 3logx 1 a
t t 0 do a nguyên dương, khi đó phương trình trở thành: 3 x t 3 3 2021
x 2020 t 2020 x 3 2021 2020 2021t x t 2020
Hàm số: 2021u 2020 2021 .uln 2021. 2020 2021u f u u f u u 0 với u 0
Nên hàm f u đơn điệu mà f 3
x f t 3 3 3log x 1
x t x a Với 1
x 0 thì vế trái nhỏ hơn 0 và vế phải lớn hơn 0 . Không tồn tại x thỏa mãn. x log x Với 3 3 log x 0 1 , x a
log x logx
1 .log a log a log x 1 Xét hàm số g x log x x 1 log x 1 x log x x g x
x xx 0 x 0 log 1 log 1 1 ln10 Bảng biến thiên:
Để tồn tại x thỏa mãn thì: log a 1 a 10
Do a nguyên dương, nên tồn tại 9 giá trị a thỏa mãn yêu cầu bài toán.
Câu 39. Gọi S là tập các số tự nhiên có 4 chữ số khác nhau được lập từ E 1; 2;3; 4; 5 . Chọn ngẫu
nhiên một số từ tập S. Xác suất để số được chọn là số chẵn bằng 1 3 3 2 A. . B. . C. . D. . 2 4 5 5 Lời giải ChọnD. 4
+ Có A số tự nhiên có 4 chữ số khác nhau được lập từ E 1; 2;3; 4; 5 . 5 1 3
-Có C .A số tự nhiên chẵn có 4 chữ số khác nhau được lập từ E 1; 2;3; 4; 5 . 2 4 1 3 C .A
+ Xác suất để số được chọn là một số chẵn là 2 2 4 . 4 A 5 5 2
x x 1 khi x 0
Câu 40. Cho hàm số f x 2x 1 khi x 0 2 2 e Biết f x a f 2sin x ln 1 .cos d x x
với a là phân số tối giản. Giá trị của a.b bằng x b b 0 e A. 60 . B. 92 . C.174 . D.132 . Lời giải ChọnB. Trang21 2 1 1 + Đặt t x t x x f x 1 x x f t 1 2sin 1 d 2 cos d 2sin 1 .cos d dt f xdx 2 2 0 1 1 2 0 1 0 1
f 2sin x 1 1 .cos d x x f x 1 dx f x 1 dx 2x 1 1 dx 11 2 x x 1 dx 2 2 2 2 12 0 1 0 1 0 2 d e x f ln x 2 2 2
+ Đặt u ln x du dx
f u dx
f x dx 29 2 x x 1 dx x x 6 e 1 1 1 2 2 e f x f ln x 23 2sin 1 .cos d x x x 4 0 e
a 23,b 4 . a b 92 .
Câu 41. Cho hai số phức
z , z thỏa mãn z 1 3i 1 và z 1 i z
5 i . Giá trị nhỏ nhất của biểu 1 2 1 2 2
thức P z 1 i z z bằng 2 2 1 2 85 A. 3. B. 10 . 1 C. 10 . 1 D. . 1 5 Lời giải ChọnD.
Gọi M , N lần lượt là điểm biểu diễn của hai số phức z , z ; C(1;1). 1 2 2 2
Ta có : M (C) : (x 1) ( y 3) 1.
N : 3x y 6 0.
P z 1 i z z NC NM . 2 2 1
Gọi (C ) đối xứng với (C) qua đường thẳng MN M N . 2 85
P NC NM NC M N
MC I C 1 1. 5
Dấu ' ' xảy ra M Mo . Câu 42. Gọi
z , z là hai trong các số phức z thỏa mãn z 3 5i 5 và z z 6. Môđun của số phức 1 2 1 2
w z z 6 10i là 1 2 A. w 16. B. w 32. C. w 8. D. w 10. Lời giải ChọnC.
Đặt w z 3 5 ;
i w z 3 5i 1 1 2 2 .
Ta có : w w 5 và w w 6 . 1 2 1 2
Mặt khác : w z z 6 10i w w . 1 2 1 2 Trang22 2 2 w w
w w 2 2 2 w w
w w 8 1 2 1 2 1 2 Do . 1 2 Vậy w 8 .
Câu 43. Cho hàm số y f x xác định và liên tục trên có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số m để phương trình f 2 2
9 x m 2022 0 có nghiệm? A. 7 B. 8 C. 4 D. 5 Lời giải Chọn D
Điều kiện xác định: 2
9 x 0 x 3 ; 3 .
Phương trình đã cho tương đương m 2 f 2022 2
9 x m 2022 0 f 2 9 x * . 2
Đặt u x 2
9 x , u x 0. Khảo sát hàm u x , ta có bảng biến thiên như sau: Phương trình * m 2022
thành f u
**. Phương trình ban đầu đã cho có nghiệm khi và 2
chỉ khi phương trình ** có nghiệm u 0;
3 . Dựa vào đồ thị đã cho, suy ra yêu cầu bài toán
tương đương với 1 m 2022 3
2021 m 2025. Vậy có 5 giá trị nguyên m thỏa mãn. 2 2 2 Trang23 f x
Câu 44. Cho hàm số f x 0 và có đạo hàm liên tục trên , thỏa mãn x f x 1 và x 2 2 f ln 2 0
. Giá trị f 3 bằng 2 1 1 A. 2 4 4ln 2 ln 5 B. 2 2 4 ln 2 ln 5 C. 4ln 2 ln52 D. 4ln 2 ln52 2 4 Lời giải Chọn D
Từ giả thiết, ta biến đổi như sau:
x f x f x f x 1 1 2 x 2 f x
x x * 2 1 2
Lấy nguyên hàm hai vế của * : f x 1 x 1 2 x x f x C 2 f x d
x x d 2 ln 1 2 x 2 2 2 ln 2 1 ln 2 1 Với f 0 2 f
0 ln C 2
ln C C 2ln 2 2 2 2 . 2 x 1
Suy ra 2 f x ln 2ln 2 * * x . 2 4 1
Thay x 3 vào ** , 2 f 3 ln 2 ln 2 4 ln 2 ln 5 f 3 4 ln 2 ln 52 . 5 4
Câu 45. Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng a . Gọi M là trung điểm của AA (tham khảo hình vẽ).
Khoảngcách từ M đến mặt phẳng AB C bằng a 21 a 2 a 2 a 21 A. . B. . C. . D. . 14 4 2 7 Lời giải ChọnA. Trang24
Gọi N là trung điểm AC AC BN
Mà AC BB nên AC NBB AB C
NBB. Có AB C
NBB B N .
Dựng BH B N H B N
. Suy ra BH AB C . 1 1 1
Ta có: d M , AB C
d A , AB C
d B, AB C BH . 2 2 2 N BB 1 1 1 1 1 7 a 21 vuông tại B nên BH . 2 2 2 2 2 2 BH BN BB a 3a 7 a 3 2 a
Vậy d M AB C 1 21 , BH . 2 14
Câu 46. Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Một mặt phẳng thay đổi, vuông góc
với cắt SO , SA, SB , SC , SD lần lượt tại I , M , N, P,Q . Một hình trụ có một đáy nội tiếp tứ
giác MNPQ và một đáy nằm trên hình vuông ABCD . Khi thể tích khối trụ lớn nhất thì độ dài SI bằng 3a 2 a 2 a 2 a A. SI . B. SI . C. SI . D. SI . 2 2 3 3 Lời giải Chọn C S E I F J K G O H
Giả sử một đáy của hình trụ tiếp xúc với các cạnh MN và PQ lần lượt tại E và F
EF là đường kính của đáy, OI là chiều cao của hình trụ
Gọi G , H lần lượt là hình chiếu của E và F lên ABCD Trang25
J , K là trung điểm của AB , CD . a 2 Ta có 2 2
SO SA .AO 2 a 3 2 2
SJ SO OJ 2 a
Đặt JG x 0 x 2 a 2x OG 2 SO Và
OI EG JG. tan EJG JG. x 2 JO 2 1 a 2x V x 2 truï 3 2 3 2 x 2
a 2x a 2x 3 2 4x 2 a a 2 .4x 48 48 3 162 3 2 a a V x truï max 162 6 a 2
SI SO OI 3 x y z
Câu 47. Trong không gian Oxyz , cho đường thẳng 1 2 1 d : và mặt cầu 1 1 1 S 2 2 2
: x y z 2x 4y 6z 13 0 . Lấy điểm M a; ;
b c với a 0 thuộc đường thẳng d
sao cho từ M kẻ được ba tiếp tuyến MA , MB , MC đến mặt cầu S ( ,
A B, C là tiếp điểm) thỏa mãn góc AMB 60
, BMC 90 , CMA 120 . Tổng a b c bằng 10 A. 2 . B. 2 . C. . D.1. 3 Lời giải Chọn A.
Mặt cầu S có tâm I 1;2; 3
, bán kính R 3 3 .
Gọi MA MB MC m .
Tam giác MAB đều AB m .
Tam giác MBC vuông cân tại M BC m 2 . Trang26
Tam giác MAC cân tại
M ,CMA 120 AC m 3 . Ta có: 2 2 2
AB BC AC ABC vuông tại B .
Gọi H là trung điểm của AC , suy ra, H là tâm đường tròn ngoại tiếp tam giác ABC
Vì MA MB MC , IA IB IC nên M , H , I thẳng hàng .
Áp dụng hệ thức lượng cho tam giác AI MAI vuông tại ,
A ta nhận được MI 6. sin 60
M d M t 1;t 2;t
1 IM t 2;t 4;t 4 .
t 0 M 1 ; 2 ;1 t / m 2 2
IM 36 3t 4t 0 . t M l a b c 2 4 1 2 7 ; ; 3 3 3 3 x 2 x 3 y 1 z 4
Câu 48. Cho hai đường thẳng
d : y t t , : và mặt phẳng 1 1 1 z 2 2t
P: x y z 2 0 . Gọi d , lần lượt là hình chiếu của d, lên mặt phẳng P . Gọi M ; a ;
b c là giao điểm của hai đường thẳng d và . Giá trị của tổng a . b c bằng A. 5 . B. 3 . C. 4 . D. 6 . Lời giải Chọn A
Ta có mặt phẳng (Q) chứa d và vuông góc với (P) : Qua A 2 ;0;2 (Q) : .
VTPT : n [u ,n ] 3 ;2; 1 (Q) d ( P)
Phương trình mặt phẳng Q là: 3
x 2 2 y 01z 2 0 3
x 2y z 4 0.
Ta có mặt phẳng (R) chứa và vuông góc với (P) : Qua B 3;1;4 (R) : .
VTPT : n [u ,n ] 0;2;2 ( R) ( P)
Phương trình mặt phẳng R là: 2 y
1 2 z 4 0 y z 5 0.
Ta có toạ độ M là nghiệm hệ phương trình 3
x 2y z 4 0 x 1
x y z 2 0
y 2 M 1
;2;3 a bc 5.
y z 5 0 z 3
x y 1
Câu 49. Cho các số dương x, y thoả mãn log
3x 2y 4. Giá trị nhỏ nhất của biểu thức 5
2x 3y 4 9
A 6x 2 y bằng x y 27 2 31 6 A. . B. . C.11 3 . D.19 . 2 4 Lời giải Chọn D
x y 1 Ta có log
3x 2y 4 5
2x 3y
log x y 1 1log 2x 3y 5x 5y 5 2x 3y 5 5 Trang27 log 5
x y 1 5 x y 1 log 2x 3y 2x 3y 1 . 5 5
Xét hàm số y f t log t t với t 0. 5
Có f t 1 1 0, t
0 nên hàm số y f t log t t đồng biến trên khoảng 0; . 5 t ln 5 Từ
1 f 5 x y
1 f 2x 3y 5 x y
1 2x 3y 3
x 2 y 5 2 . 4 9
Lại có A 6x 2y
x y 4 9 3 2 9x 4y x y x y
Từ 2 và áp dụng bất đẳng thức Côsi cho 2 số không âm ta có A 4 9 5 2 9 . x 2 4 . y 5 1212 19 . x y 3
x 2y 5 2 x
Dấu “=” xảy ra khi và chỉ khi 4 3 9 x . x 3 y 9 2 4 y y
Câu 50. Cho f x là hàm đa thức bậc 6 sao cho đồ thị hàm số y f x như hình vẽ và f 2 0 , f 1 0.
Số điểm cực tiểu của hàm số y f 2
x 4x 5 là: A. 7 . B. 4 . C. 3 . D. 5 . Lời giải Chọn B
Xét hàm số g x f 2
x x g x x f 2 4 5 2 4
x 4x 5 x 2 3 a x 2 2 b x 2 x 3 2
x 4x 5 2
Ta có g x 0 x 2 2
x 4x 5 3 2 x 1
x 4x 5 4 x 2 2 c x 2 3 d Trang28
Do f 2 0 , f
1 0 nên phương trình g x 0 có 4 nghiệm đơn phân biệt nên hàm số y f 2
x 4x 5 có 4 điểm cực tiểu. Trang29




