Đề Thi Toán 12 Học Kỳ 2 Quảng Nam 2020-2021 Có Đáp Án Và Lời Giải Chi Tiết

Đề thi Toán 12 HK2 Quảng Nam 2020 - 2021 được biên soạn dưới dạng file PDF gồm 19 trang. Tài liệu là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

34 17 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang 1

ĐỀ CHÍNH THỨC

SỞ GIÁO DỤC VÀ ĐÀO TẠO

QUẢNG NAM

(Đề gồm có 03 trang)

KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021

Môn: TOÁN – Lớp 12

Thời gian: 60 phút (không kể thời gian giao đề)

MÃ ĐỀ

Họ và tên học sinh:………………………………………………….………….Lớp:……………

Câu 1. Tìm số thuần ảo trong các số phức sau đây

2 i

. B.

2 i

. C.

. D.

Câu 2. Nếu

 

d3f x x 



và

 

d2g x x 



thì

   

df x g x x







bằng

1

. B.

5

. C.

. D.

Câu 3. Nếu

 

2 d 4f x x 



thì

 

df x x



bằng

. B.

. C.

. D.

Câu 4. Cho

 

là một nguyên hàm của hàm số

 

trên

 

1;2

. Mệnh đề nào sau đây đúng?

     

d 2 1f x x F F



. B.

     

d 2 1f x x F F



     

d 1 2f x x F F



. D.

     

d 2 1f x x f f



Câu 5. Trong không gian

Oxyz

, vectơ

23u i j k  

   

có tọa độ là

 

2;1; 3

. B.

 

2; 1;3

. C.

 

2;0;3

. D.

 

2;0; 3

Câu 6. Số phức liên hợp của số phức

25zi

là

25zi  

. B.

52zi

. C.

25zi

. D.

52zi

Câu 7. Trong không gian

Oxyz

, mặt phẳng nào sau đây đi qua gốc tọa độ?

 

: 2 0P x y z  

. B.

 

: 2 3 0P x y  

 

: 1 0P y z  

. D.

 

: 3 0P x z  

Câu 8. Trong không gian

Oxyz

, tích vô hướng của hai vectơ

 

2;0; 1a 



và

 

3;1;0b 



bằng

Trang 2

1

. B.

4

. C.

5

. D.

6

Câu 9.

cos



bằng

cot xC

. B.

tanxC

. C.

cot xC

. D.

tan xC

Câu 10. Trên mặt phẳng tọa độ,điểm biểu diễn của số phức

13i

có tọa độ là

 

1;3

. B.

 

3;1

. C.

 

1; 3

. D.

 

3; 1

Câu 11. Trong không gian với hệ tọa độ

Oxyz

cho cho hai điểm

 

1;2;2A

và

 

3;1;0B

. Tọa độ của

vectơ



là

 

4; 3; 2  

. B.

 

2; 1; 2

. C.

 

2;1;2

. D.

 

4;3;2

Câu 12. Họ tất cả các nguyên hàm của hàm số

 





là

ln 2xC

. B.

ln 2

xC

. C.

 

ln 2xC

. D.

ln 2

xC

Câu 13. Tính



3 d 3 ln3

xC



. B.









ln3

xC



. D.





Câu 14. Trong không gian

Oxyz

, mặt cầu

     

: 1 2 4S x y z    

có bán kính bằng

. B.

. C.

. D.

Câu 15. Trong không gian

Oxyz

, đường thẳng vuông góc với mặt phẳng

 

: 2 3 0P x y z   

có một

vectơ chỉ phương là

 

0; 1;2u 



. B.

 

1;2; 3u 



. C.

 

1;2; 3u   



. D.

 

1; 1;2u 



Câu 16. Trong không gian

Oxyz

, cho tứ diện

ABCD

với

 

3; 1;1A 

và mặt phẳng

 

BCD

có phương

trình

2 2 5 0x y z   

. Chiều cao

của tứ diện

ABCD

bằng

. B.

. C.

. D.

6 11

Trang 3

Câu 17. Trong không gian

Oxyz

, cho hai điểm

 

2;1;0M

và

 

1;2; 2N 

. Mặt phẳng

 

vuông góc

với

tại điểm

có phương trình

2 1 0x y z   

. B.

3 3 2 13 0x y z   

3 3 2 9 0x y z   

. D.

2 5 0x y z   

Câu 18. Khi tìm nguyên hàm

 

x 



, bằng cách đặt

3tx

ta được nguyên hàm nào sau đây?



. B.



. C.



. D.



Câu 19. Cho số phức

43zi=+

và

w2i=+

. Số phức

wz +

bằng

32i+

. B.

24i+

. C.

64i+

. D.

22i+

Câu 20. Cho hình phẳng

( )

giới hạn bởi đồ thị hàm số

, trục hoành và các đường thẳng

1x=

2x =

. Khối tròn xoay tạo thành khi quay

( )

quanh trục hoành có thể tích bằng

. B.

. C.

. D.

ln15p

Câu 21. Cho số phức

thoả mãn

2 12 3z z i+ = +

. Phần ảo của

bằng

. B.

. C.

. D.

Câu 22. Biết

ln d ln2x x a b



trong đó

,ab

là các số nguyên. Tính

ab

3ab

. B.

2ab  

. C.

1ab

. D.

2ab

Câu 23. Hàm số nào sau đây là một nguyên hàm của hàm số

 

f x x

e e 1

x 

. B.

x 

. C.



. D.

e e 1

x 

Câu 24. Cho số phức

thỏa mãn

 

3 4 10iz

. Môđun của số phức

bằng

. B.

. C.

. D.

Câu 25. Trong không gian

Oxyz

, đường thẳng đi qua hai điểm

   

1;0;2 , 4;1;0AB

có phương trình

tham số là

  















. B.

  











  



. C.

















. D.













  



Trang 4

Câu 26. Có tất cả bao nhiêu số phức

thỏa mãn

là số thực và

22zi  

A.2. B. 1. C. 4. D. 3.

Câu 27. Cho hàm số

yx

có đồ thị

 

và

 

là tiếp tuyến với

 

tại điểm có hoành độ

3x 

(tham khảo hình vẽ bên).

Diện tích hình phẳng giới hạn bởi

 

và trục hoành bằng

. B.

. C.

. D.

Câu 28. Trong không gian

Oxyz

cho mặt phẳng

 

vuông góc với mặt phẳng

 

:2 0Q x y z  

và

cắt các trục

,,Ox Oy Oz

lần lượt tại

     

2;0;0 , 0; ;0 , 0;0;A B b C c

với

0, 0bc

sao cho thể

tích khối tứ diện

.O ABC

bằng

. Giá trị

bc

bằng

6

. B.

9

. C.

. D.

Câu 29. Cho số phức

thỏa mãn

 

24z i z

là số thuần ảo. Trên mặt phẳng tọa độ , tập hợp điểm

biểu diễn số phức

là đường tròn có bán kính bằng

. B.

. C.

. D.

Câu 30. Trong không gian

Oxyz

, cho mặt cầu

 

có tâm

 

1; 2;3I 

và cắt trục

tại hai điểm

sao cho

4AB 

. Phương trình mặt cầu

 

là:

     

2 2 2

1 2 3 10x y z     

. B.

     

2 2 2

1 2 3 6x y z     

     

2 2 2

1 2 3 8x y z     

. D.

     

2 2 2

1 2 3 14x y z     

Câu 31. Trong không gian

Oxyz

, cho mặt phẳng

 

2 2 1 0x y z   

; điểm

 

5; 1; 4A 

và mặt

cầu

 

có tâm

 

;;I a b c

cắt mặt phẳng

 

theo giao tuyến là đường tròn

 

có bán kính

2r 

. Biết rằng mọi điểm

thuộc

 

thì

là tiếp tuyến của

 

. Giá trị của

abc

bằng:

Trang 5

. B.

3

. C.



. D.

Câu 32. Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;

, thỏa mãn

   

e . e e 1

x x x

x f f



  

với mọi

x

và

 

11f 

. Giá trị

 

thuộc khoảng nào sau đây?

 

3;4

. B.

 

2;3

. C.

 

4;5

. D.

 

5;6

ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT

BẢNG ĐÁP ÁN

LỜI GIẢI CHI TIẾT

Câu 1. Tìm số thuần ảo trong các số phức sau đây

2 i

. B.

2 i

. C.

. D.

Lời giải

Chọn D

Số phức thuần ảo là

Câu 2. Nếu

 

d3f x x 



và

 

d2g x x 



thì

   

df x g x x







bằng

1

. B.

5

. C.

. D.

Lời giải

Chọn C

Ta có

         

1 1 1

0 0 0

d d d 3 2 5f x g x x f x x g x x      





  

Câu 3. Nếu

 

2 d 4f x x 



thì

 

df x x



bằng

. B.

. C.

. D.

Trang 6

Lời giải

Chọn A

Ta có

     

3 3 3

1 1 1

2 d 4 2 d 4 d 2f x x f x x f x x    

  

Câu 4. Cho

 

là một nguyên hàm của hàm số

 

trên

 

1;2

. Mệnh đề nào sau đây đúng?

     

d 2 1f x x F F



. B.

     

d 2 1f x x F F



     

d 1 2f x x F F



. D.

     

d 2 1f x x f f



Lời giải

Chọn A

Ta có:

       

d 2 1f x x F x F F  



Câu 5. Trong không gian

Oxyz

, vectơ

23u i j k  

   

có tọa độ là

 

2;1; 3

. B.

 

2; 1;3

. C.

 

2;0;3

. D.

 

2;0; 3

Lời giải

Chọn A

Ta có:

23u i j k  

   

suy ra

       

2 1;0;0 0;1;0 3 0;0;1 2;1; 3u     



Câu 6. Số phức liên hợp của số phức

25zi

là

25zi  

. B.

52zi

. C.

25zi

. D.

52zi

Lời giải

Chọn C

Ta có:

25zi

suy ra

25zi

Trang 7

Câu 7. Trong không gian

Oxyz

, mặt phẳng nào sau đây đi qua gốc tọa độ?

 

: 2 0P x y z  

. B.

 

: 2 3 0P x y  

 

: 1 0P y z  

. D.

 

: 3 0P x z  

Lời giải

Chọn A

Thay tọa độ

 

0;0;0O

vào phương trình mặt phẳng

 

: 2 0P x y z  

ta được:

2.0 0 0 0  

Vậy

 

: 2 0P x y z  

đi qua gốc tọa độ.

Câu 8. Trong không gian

Oxyz

, tích vô hướng của hai vectơ

 

2;0; 1a 



và

 

3;1;0b 



bằng

1

. B.

4

. C.

5

. D.

6

Lời giải

Chọn D

   

. 2. 3 0.1 1 .0 6ab      



Câu 9.

cos



bằng

cot xC

. B.

tanxC

. C.

cot xC

. D.

tan xC

Lời giải

Chọn D

Ta có:

d tan

cos

x x C





Câu 10. Trên mặt phẳng tọa độ,điểm biểu diễn của số phức

13i

có tọa độ là

 

1;3

. B.

 

3;1

. C.

 

1; 3

. D.

 

3; 1

Lời giải

Trang 8

Chọn C

Câu 11. Trong không gian với hệ tọa độ

Oxyz

cho cho hai điểm

 

1;2;2A

và

 

3;1;0B

. Tọa độ của

vectơ



là

 

4; 3; 2  

. B.

 

2; 1; 2

. C.

 

2;1;2

. D.

 

4;3;2

Lời giải

Chọn B

Ta có

 

2; 1; 2AB   



Câu 12. Họ tất cả các nguyên hàm của hàm số

 





là

ln 2xC

. B.

ln 2

xC

. C.

 

ln 2xC

. D.

ln 2

xC

Lời giải

Chọn A

Ta có

ln 2

dx x C

  





Câu 13. Tính



3 d 3 ln3

xC



. B.









ln3

xC



. D.





Lời giải

Chọn C

Trang 9

Áp dụng công thức nguyên hàm, ta có

ln3

xC



Câu 14. Trong không gian

Oxyz

, mặt cầu

     

: 1 2 4S x y z    

có bán kính bằng

. B.

. C.

. D.

Lời giải

Chọn A

Mặt cầu

     

: 1 2 4S x y z    

, suy ra bán kính

42R 

Câu 15. Trong không gian

Oxyz

, đường thẳng vuông góc với mặt phẳng

 

: 2 3 0P x y z   

có một

vectơ chỉ phương là

 

0; 1;2u 



. B.

 

1;2; 3u 



. C.

 

1;2; 3u   



. D.

 

1; 1;2u 



Lời giải

Chọn D

Mặt phẳng

 

: 2 3 0P x y z   

có VTPT là

 

1; 1;2

n 



Đường thẳng vuông góc với mặt phẳng

 

suy ra VTCP của đường thẳng cùng phương với

VTPT của mặt phẳng

 

hay

 

1; 1;2

u kn k  



Chọn

1k 

suy ra ta có một VTCP của đường thẳng là

 

1; 1;2u 



Câu 16. Trong không gian

Oxyz

, cho tứ diện

ABCD

với

 

3; 1;1A 

và mặt phẳng

 

BCD

có phương

trình

2 2 5 0x y z   

. Chiều cao

của tứ diện

ABCD

bằng

. B.

. C.

. D.

6 11

Lời giải

Chọn B

Chiều cao của tứ diện

ABCD

là khoảng cách từ

đến

 

BCD

Trang 10

Khi đó ta có

 

3 2. 1 2.1 5

d , 2

1 2 2

AH A BCD

   

  

  

Câu 17. Trong không gian

Oxyz

, cho hai điểm

 

2;1;0M

và

 

1;2; 2N 

. Mặt phẳng

 

vuông góc

với

tại điểm

có phương trình

2 1 0x y z   

. B.

3 3 2 13 0x y z   

3 3 2 9 0x y z   

. D.

2 5 0x y z   

Lời giải

Chọn D

Ta có

 

1;1; 2MN   

uuur

Do

 

MN P

nên ta chọn

 

có VTPT

 

1; 1;2

n MN

uuur uuur

   

Suy ra phương trình

 

là

   

1 2 2 2 0 2 5 0x y z x y z          

Câu 18. Khi tìm nguyên hàm

 

x 



, bằng cách đặt

3tx

ta được nguyên hàm nào sau đây?



. B.



. C.



. D.



Lời giải

Chọn A

Đặt

3 d 2 d 2d 4 dt x t x x t x x     

Vậy ta có

 







với

3tx

Câu 19. Cho số phức

43zi=+

và

w2i=+

. Số phức

wz +

bằng

32i+

. B.

24i+

. C.

64i+

. D.

22i+

Lời giải

Chọn C

Trang 11

Ta có

( ) ( )

w 4 3 2 6 4z i i i+ = + + + = +

Câu 20. Cho hình phẳng

( )

giới hạn bởi đồ thị hàm số

, trục hoành và các đường thẳng

1x=

2x =

. Khối tròn xoay tạo thành khi quay

( )

quanh trục hoành có thể tích bằng

. B.

. C.

. D.

ln15p

Lời giải

Chọn A

Thể tích khối tròn xoay cần tính là

d ln 2 1 ln

2 1 2 2 3

V x x

p= = + =

Câu 21. Cho số phức

thoả mãn

2 12 3z z i+ = +

. Phần ảo của

bằng

. B.

. C.

. D.

Lời giải

Chọn C

Đặt

z x yi=+

( )

,xyÎ ¡

Theo đề

( )

3 12 4

2 12 3 2 12 3 3 12 3

z z i x yi x yi i x yi i

ìì

ïï

+ = + Û + + - = + Û - = + Û Û

íí

ïï

- = = -

ïï

îî

Vậy phần ảo của số phức

là

Câu 22. Biết

ln d ln2x x a b



trong đó

,ab

là các số nguyên. Tính

ab

3ab

. B.

2ab  

. C.

1ab

. D.

2ab

Lời giải

Chọn C

Trang 12

Đặt























Ta có:

2 2 2

1 1 1

ln d ln . d 2ln2 d 2ln2 2ln2 1x x x x x x x x

       

  

Vậy

2, 1 1a b a b     

Câu 23. Hàm số nào sau đây là một nguyên hàm của hàm số

 

f x x

e e 1

x 

. B.

x 

. C.



. D.

e e 1

x 

Lời giải

Chọn D

Ta có:

 

d e d

f x x x x



Đặt

d e d e

u x u x

v x v













Khi đó:

 

d e e d e e

x x x x

f x x x x x C    



e e 1

x  

là một nguyên hàm của hàm

 

f x x

Câu 24. Cho số phức

thỏa mãn

 

3 4 10iz

. Môđun của số phức

bằng

. B.

. C.

. D.

Lời giải

Chọn C

Trang 13

Ta có:

 

10 6 8 6 8

3 4 10 2

3 4 5 5 5 5

i z z i z

   

          

   



   

Câu 25. Trong không gian

Oxyz

, đường thẳng đi qua hai điểm

   

1;0;2 , 4;1;0AB

có phương trình

tham số là

  















. B.

  











  



. C.

















. D.













  



Lời giải

Chọn C

Ta có

 

3;1; 2AB 



Phương trình đường thẳng

đi qua điểm

và nhận véctơ

 

3;1; 2AB 



là véctơ chỉ

phương

















Câu 26. Có tất cả bao nhiêu số phức

thỏa mãn

là số thực và

22zi  

A.2. B. 1. C. 4. D.3.

Lời giải

Chọn D

Gọi số phức

 

,,z a bi a b  

Theo giả thiết có

 

2 2 2

2z a bi a b abi    

là số thực nên

0ab 

Mặt khác

     

2 2 2 1 2 2 1 4z i a b i a b            

Trang 14

Từ đó, ta có hệ

   

2 1 4





































   





























Vậy có 3 số phức thỏa mãn yêu cầu bài toán.

Câu 27. Cho hàm số

yx

có đồ thị

 

và

 

là tiếp tuyến với

 

tại điểm có hoành độ

3x 

(tham khảo hình vẽ bên).

Diện tích hình phẳng giới hạn bởi

 

và trục hoành bằng

. B.

. C.

. D.

Lời giải

Chọn A

Trang 15

Ta có

y x y x  

Phương trình tiếp tuyến

biết

 

' 3 2

















là

 

2 3 3 2 3y x y x     

Giao điểm của

với trục hoành là

x 

Từ hình vẽ ta thấy, diện tích hình phẳng giới hạn bởi

 

và trục hoành là

 

d 2 3 d

S x x x x   



Câu 28. Trong không gian

Oxyz

cho mặt phẳng

 

vuông góc với mặt phẳng

 

:2 0Q x y z  

và

cắt các trục

,,Ox Oy Oz

lần lượt tại

     

2;0;0 , 0; ;0 , 0;0;A B b C c

với

0, 0bc

sao cho thể

tích khối tứ diện

.O ABC

bằng

. Giá trị

bc

bằng

6

. B.

9

. C.

. D.

Lời giải

Chọn D

Do mặt phẳng

 

cắt các trục

,,Ox Oy Oz

lần lượt tại

     

2;0;0 , 0; ;0 , 0;0;A B b C c

nên

 

: 1 2 2 2 0

x y z

P bcx cy bz bc

       

Khi đo



 

có véc tơ pháp tuyến là:

 

;2 ;2

n bc c b



Trang 16

Mặt phẳng

 

có véc tơ pháp tuyến là:

 

2;1; 1

n 



Vì

   

. 0 2 2 2 0 0

P Q n n bc c b bc c b          

 

(1).

Ta có

6 6 3

O ABC

bc bc

V OAOB OC  

. Theo bài ra thì

3 3 9

O ABC

V bc    

Từ (1) suy ra

9 0 9c b b c     

Câu 29. Cho số phức

thỏa mãn

 

24z i z

là số thuần ảo. Trên mặt phẳng tọa độ , tập hợp điểm

biểu diễn số phức

là đường tròn có bán kính bằng

. B.

. C.

. D.

Lời giải

Chọn C

Đặt

 

,,z x yi x y  

Ta có

 

     

2 4 2 4z i z x y i x yi      

  

  

      

4 2 4 2x x y y xy x y i       





Khi đo



 

24z i z

là số thuần ảo

   

4 2 0x x y y    

   

4 2 0 2 1 5x y x y x y         

Vậy tập hợp điểm biểu diễn số phức

là đường tròn có bán kính là

5R 

Câu 30. Trong không gian

Oxyz

, cho mặt cầu

 

có tâm

 

1; 2;3I 

và cắt trục

tại hai điểm

sao cho

4AB 

. Phương trình mặt cầu

 

là:

     

2 2 2

1 2 3 10x y z     

. B.

     

2 2 2

1 2 3 6x y z     

     

2 2 2

1 2 3 8x y z     

. D.

     

2 2 2

1 2 3 14x y z     

Lời giải

Chọn D

Trang 17

 Gọi

là hình chiếu của tâm

lên trục

 

0; 2;0H 



10IH 

 Bán kính mặt cầu

 

là:

2 2 2 2

R AH IH IH



    





 Phương trình mặt cầu

 

là:

       

2 2 2

1 2 3 14S x y z      

Câu 31. Trong không gian

Oxyz

, cho mặt phẳng

 

2 2 1 0x y z   

; điểm

 

5; 1; 4A 

và mặt

cầu

 

có tâm

 

;;I a b c

cắt mặt phẳng

 

theo giao tuyến là đường tròn

 

có bán kính

2r 

. Biết rằng mọi điểm

thuộc

 

thì

là tiếp tuyến của

 

. Giá trị của

abc

bằng:

. B.

3

. C.



. D.

Lời giải

Chọn D

Trang 18

Ta có:

 

2 2 2

2.5 1 2. 4 1

2 1 2

d d A P

   

  



Do mọi điểm

thuộc

 

thì

là tiếp tuyến của

 

nên

thuộc mặt cầu tâm

. Mặt

cầu này cắt mặt cầu

 

theo giao là đường tròn

 

nên hình chiếu của

và

trên mặt

phẳng

 

đều là tâm

của đường tròn

 

là tiếp tuyến của

 

nên

và

nằm khác phía so với mặt phẳng

 

và tam giác

MAI

vuông tại

nên

.HA HI HM



HM r

HI HA

HA d

   



HI AH

 

Mặt phẳng

 

có một vector pháp tuyến

 

2; 1; 2n   



 

AH P

nên

có một vector chỉ phương là

 

2; 1; 2n   





Phương trình







  





  



 

H AH P 

nên tọa độ

thỏa mãn hệ:

2 2 1 0

x y z







  





  



   



























 

1;1;0H



5 11 4

;;

9 9 9









a 

;

b 

;

c 



abc  

Câu 32. Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;

, thỏa mãn

   

e . e e 1

x x x

x f f



  

với mọi

x

và

 

11f 

. Giá trị

 

thuộc khoảng nào sau đây?

 

3;4

. B.

 

2;3

. C.

 

4;5

. D.

 

5;6

Lời giải

Chọn D

Ta có:

   

e . e e 1

x x x

x f f



  



   

 

e e e 1 e

x x x x

f f x





  



 

e e 1 e

x x x













 

ln4 ln4

e e d 1 e d

x x x

f x x x















 

ln4

e e 1 e d

x x x

f x x













     

ln4

4 1 1 e d

f f x x



  



Đặt

d e d



























Trang 19



     

ln4

4 1 1 e e d

f f x x





    







   

ln4

4 1 1 ln4 1 e



     



   

4 4 ln4 5,39 5;6f    

Bấm Tải xuống để xem toàn bộ.

| 1/19

| | Tải xuống

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – Lớp 12 ĐỀ CHÍNH THỨC
Thời gian: 60 phút (không kể thời gian giao đề) MÃ ĐỀ
(Đề gồm có 03 trang)
Họ và tên học sinh:………………………………………………….………….Lớp:…………… Câu 1.
Tìm số thuần ảo trong các số phức sau đây
A. 2  i .
B. 2  i . C. 2 . D. 2i . 1 1 1 Câu 2. Nếu f
 xdx  3 và gxdx  2   thì  f
 x gxdx  bằng 0 0 0 A. 1 . B. 5  . C. 5 . D. 1 . 3 3 Câu 3. Nếu 2 f
 xdx  4 thì f xdx  bằng 1 1 A. 2 . B. 8 . C. 6 . D. 4 . Câu 4.
Cho F  x là một nguyên hàm của hàm số f  x trên 1; 2 . Mệnh đề nào sau đây đúng? 2 2 A. f
 xdx  F 2F  1 . B. f
 xdx  F2 F 1 . 1 1 2 2 C. f
 xdx  F  1F 2 . D. f
 xdx  f 2 f  1 . 1 1     Câu 5.
Trong không gian Oxyz , vectơ u  2i  j  3k có tọa độ là A. 2;1;  3 . B.  2  ;1;3. C.  2  ;0;3 . D. 2;0; 3   . Câu 6.
Số phức liên hợp của số phức z  2  5i là A. z  2   5i .
B. z  5  2i .
C. z  2  5i .
D. z  5  2i . Câu 7.
Trong không gian Oxyz , mặt phẳng nào sau đây đi qua gốc tọa độ?
A. P : 2x  y  z  0 .
B.  P : 2x  y  3  0 . 1  3 
C.  P : y  z 1  0 .
D.  P : x  z  3  0 . 2  4    Câu 8.
Trong không gian Oxyz , tích vô hướng của hai vectơ a  2;0;  
1 và b  3;1;0 bằng Trang 1 A. 1. B. 4  . C. 5  . D. 6  . 1 Câu 9. dx  bằng 2 cos x
A. cot x  C .
B.  tan x  C .
C. cot x  C .
D. tan x  C .
Câu 10. Trên mặt phẳng tọa độ,điểm biểu diễn của số phức1 3i có tọa độ là A. 1;3 . B. 3;  1 . C. 1;  3 . D. 3;   1 .
Câu 11. Trong không gian với hệ tọa độ Oxyz cho cho hai điểm A1; 2; 2và B 3;1;0 . Tọa độ của  vectơ AB là A.  4  ; 3; 2 .
B. 2; 1; 2 . C.  2  ;1;2 . D. 4;3;2 .
Câu 12. Họ tất cả các nguyên hàm của hàm số f  x 1  x là 2 1 1
A. ln x  2  C . B.
ln x  2  C .
C. ln  x  2  C . D.
ln x  2  C . 2 2
Câu 13. Tính 3xdx  . x 1  x 3
A. 3xd  3x x ln 3  C  . B. 3 dx   C  . x  1 x 3x x 3x C. 3 dx   C  . D. 3 dx   C  . ln 3 ln x 2 2
Câu 14. Trong không gian Oxyz , mặt cầu S   x   2 :
1  y   z  2  4 có bán kính bằng A. 4 . B. 2 . C.16 . D. 2
Câu 15. Trong không gian Oxyz , đường thẳng vuông góc với mặt phẳng  P : x  y  2z  3  0 có một
vectơ chỉ phương là     A. u       3 0; 1;2.
B. u  1; 2; 3 . C. u  1; 2; 3 .
D. u  1; 1; 2 . 1   2   4  
Câu 16. Trong không gian Oxyz , cho tứ diện ABCD với A3; 1 
;1 và mặt phẳng  BCD có phương
trình x  2 y  2z  5  0 . Chiều cao AH của tứ diện ABCD bằng 2 1 6 11 A. . B. 2 . C. . D. . 3 3 11 Trang 2
Câu 17. Trong không gian Oxyz , cho hai điểm M 2;1;0 và N 1; 2;  2 . Mặt phẳng  P vuông góc
với MN tại điểm N có phương trình
A. x  y  2z 1  0 .
B. 3x  3y  2z 13  0 .
C. 3x  3y  2z  9  0 .
D. x  y  2z  5  0 . 4x
Câu 18. Khi tìm nguyên hàm    
x , bằng cách đặt 2 t x
3 ta được nguyên hàm nào sau đây? x  3 d 2 2 2 1 1 4 A. dt  . B. dt  . C. dt  . D. dt  . 2 t 2 t 2 2t 2 t
Câu 19. Cho số phức z = 4+ 3i và w = 2 + i . Số phức z + w bằng A. 3+ 2i . B. 2 + 4i . C. 6 + 4i . D. 2+ 2i .
Câu 20. Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số 1 y =
, trục hoành và các đường thẳng 2x + 1
x = 1, x = 2 . Khối tròn xoay tạo thành khi quay (H ) quanh trục hoành có thể tích bằng p 5 1 5 5 A. ln . B. ln . C. p ln . D. p ln15. 2 3 2 3 3
Câu 21. Cho số phức z thoả mãn z + 2z = 12 + 3i . Phần ảo của z bằng A. 3 . B. 4 . C.- 3 . D.- 4 . 2 Câu 22. Biết ln d
x x  a ln 2  b 
trong đó a, b là các số nguyên. Tính a  b . 1
A. a  b  3.
B. a  b  2  .
C. a  b 1.
D. a  b  2 .
Câu 23. Hàm số nào sau đây là một nguyên hàm của hàm số    ex f x x ? 2 x A. ex ex x  1 . B. ex x 1 . C. ex 1. D. ex ex x  1. 2
Câu 24. Cho số phức z thỏa mãn 3  4i z  10 . Môđun của số phức z bằng 5 2 1 A. . B. . C. 2 . D. . 2 5 2
Câu 25. Trong không gian Oxyz , đường thẳng đi qua hai điểm A1;0; 2, B 4;1;0 có phương trình tham số là x  3   t x  1   3t x 1 3t x  3 t     A.  y  1  .
B.  y  t .
C.  y  t . D.  y  1 .     z  2  2t  z  2   2t  z  2  2t  z  2   2t  Trang 3
Câu 26. Có tất cả bao nhiêu số phức z thỏa mãn 2
z là số thực và z  2  i  2 ? A.2. B. 1. C. 4. D. 3. 1 Câu 27. Cho hàm số 2 y 
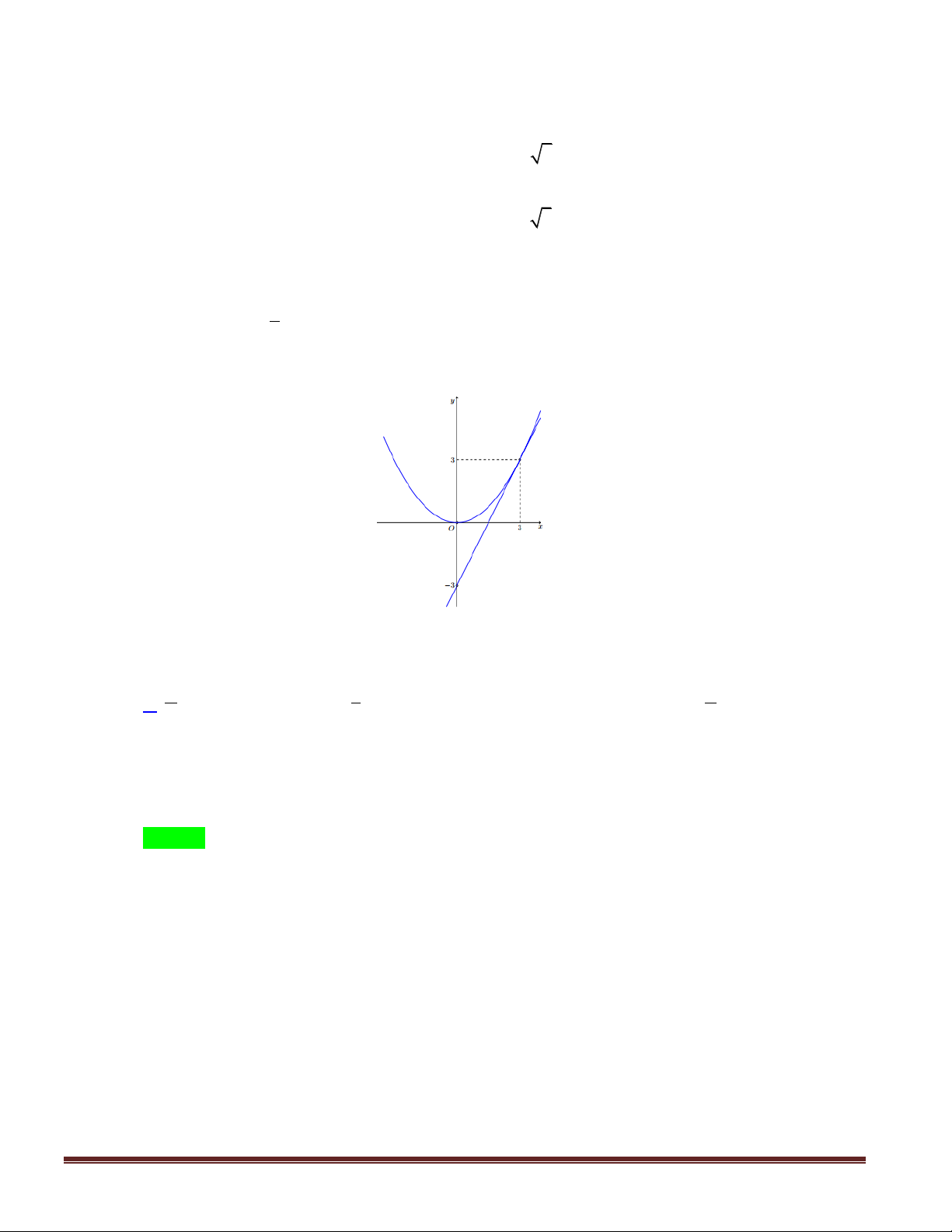
x có đồ thị P và d  là tiếp tuyến với P tại điểm có hoành độ x  3 3
(tham khảo hình vẽ bên).
Diện tích hình phẳng giới hạn bởi  P , d  và trục hoành bằng 3 3 9 A. . B. . C. 3 . D. . 4 8 4
Câu 28. Trong không gian Oxyz cho mặt phẳng  P vuông góc với mặt phẳng Q : 2x  y  z  0 và
cắt các trục Ox, Oy, Oz lần lượt tại A2;0;0, B 0; ;
b 0,C 0;0;c với b  0, c  0 sao cho thể tích khối tứ diện .
O ABC bằng 3 . Giá trị b  c bằng A. 6  . B. 9  . C. 9 . D. 6 .
Câu 29. Cho số phức z thỏa mãn z  2iz  4 là số thuần ảo. Trên mặt phẳng tọa độ , tập hợp điểm
biểu diễn số phức z là đường tròn có bán kính bằng A. 3 . B. 5 . C. 5 . D. 3 .
Câu 30. Trong không gian Oxyz , cho mặt cầu S  có tâm I 1;  2;3 và cắt trục Oy tại hai điểm A , B
sao cho AB  4 . Phương trình mặt cầu S  là: 2 2 2 2 2 2 A.  x  
1   y  2   z  3  10. B.  x  
1   y  2   z   3  6 . 2 2 2 2 2 2 C.  x  
1   y  2   z  3  8 . D.  x  
1   y  2   z  3  14 .
Câu 31. Trong không gian Oxyz , cho mặt phẳng  P : 2x  y  2z 1  0 ; điểm A5;1; 4 và mặt
cầu S  có tâm I a ;b;c cắt mặt phẳng  P theo giao tuyến là đường tròn C có bán kính
r  2 . Biết rằng mọi điểm M thuộc C thì AM là tiếp tuyến của S  . Giá trị của a  b  c bằng: Trang 4 20 20 A. 3 . B. 3  . C.  . D. . 9 9
Câu 32. Cho hàm số y  f  x có đạo hàm liên tục trên 0;   , thỏa mãn  ex. ex   ex x f f 1
với mọi x  và f  
1  1. Giá trị f 4 thuộc khoảng nào sau đây? A. 3; 4 . B. 2;3 . C. 4;5 . D. 5;6 .
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 D C A A A C A D D C B A C B D B 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 D A C A C C D C C D A C C D D D
LỜI GIẢI CHI TIẾT Câu 1.
Tìm số thuần ảo trong các số phức sau đây
A. 2  i .
B. 2  i . C. 2 . D. 2i . Lời giải Chọn D
Số phức thuần ảo là 2i 1 1 1 Câu 2. Nếu f
 xdx  3 và gxdx  2   thì  f
 x gxdx  bằng 0 0 0 A. 1 . B. 5  . C. 5 . D. 1 . Lời giải Chọn C 1 1 1 Ta có  f
 x gxdx  f 
 xdx g
 xdx  3 2    5 . 0 0 0 3 3 Câu 3. Nếu 2 f
 xdx  4 thì f xdx  bằng 1 1 A. 2 . B. 8 . C. 6 . D. 4 . Trang 5 Lời giải Chọn A 3 3 3 Ta có 2 f
 xdx  4 2 f
 xdx  4 f
 xdx  2 . 1 1 1 Câu 4.
Cho F  x là một nguyên hàm của hàm số f  x trên 1; 2 . Mệnh đề nào sau đây đúng? 2 2 A. f
 xdx  F2F  1 . B. f
 xdx  F2 F 1 . 1 1 2 2 C. f
 xdx  F 1F2 . D. f
 xdx  f 2 f  1 . 1 1 Lời giải Chọn A 2 2 Ta có: f
 xdx  F x  F 2F  1. 1 1     Câu 5.
Trong không gian Oxyz , vectơ u  2i  j  3k có tọa độ là A. 2;1;  3 . B.  2  ;1;3. C.  2  ;0;3 . D. 2;0; 3   . Lời giải Chọn A     
Ta có: u  2i  j  3k suy ra u  21;0;0   0;1;0  30;0  ;1  2;1;  3 . Câu 6.
Số phức liên hợp của số phức z  2  5i là A. z  2   5i .
B. z  5  2i .
C. z  2  5i .
D. z  5  2i . Lời giải Chọn C
Ta có: z  2  5i suy ra z  2  5i . Trang 6 Câu 7.
Trong không gian Oxyz , mặt phẳng nào sau đây đi qua gốc tọa độ?
A. P : 2x  y  z  0 .
B.  P : 2x  y  3  0 . 1  3 
C.  P : y  z 1  0 .
D.  P : x  z  3  0 . 2  4  Lời giải Chọn A
Thay tọa độ O 0;0;0 vào phương trình mặt phẳng P : 2x  y  z  0 ta được: 2.0  0  0  0 . 3 
Vậy P : 2x  y  z  0 đi qua gốc tọa độ. 3    Câu 8.
Trong không gian Oxyz , tích vô hướng của hai vectơ a  2;0;  
1 và b  3;1;0 bằng A. 1. B. 4  . C. 5  . D. 6  . Lời giải Chọn D   . a b  2. 3    0.1   1 .0  6  . 1 Câu 9. dx  bằng 2 cos x
A. cot x  C .
B.  tan x  C .
C. cot x  C .
D. tan x  C . Lời giải Chọn D 1 Ta có:
dx  tan x  C  . 2 cos x
Câu 10. Trên mặt phẳng tọa độ,điểm biểu diễn của số phức1 3i có tọa độ là A. 1;3 . B. 3;  1 . C. 1;  3 . D. 3;   1 . Lời giải Trang 7 Chọn C
Câu 11. Trong không gian với hệ tọa độ Oxyz cho cho hai điểm A1; 2; 2và B 3;1;0 . Tọa độ của  vectơ AB là A.  4  ; 3; 2 .
B. 2; 1;  2 . C.  2  ;1;2 . D. 4;3; 2 . Lời giải Chọn B 
Ta có AB  2; 1;  2 .
Câu 12. Họ tất cả các nguyên hàm của hàm số f  x 1  x là 2 1 1
A. ln x  2  C . B.
ln x  2  C .
C. ln  x  2  C . D.
ln x  2  C . 2 2 Lời giải Chọn A 1 Ta có
dx  ln x  2  C  . x  2
Câu 13. Tính 3xdx  . x 1  x 3
A. 3xd  3x x ln 3  C  . B. 3 dx   C  . x  1 x 3x x 3x C. 3 dx   C  . D. 3 dx   C  . ln 3 ln x Lời giải Chọn C Trang 8 x 3x
Áp dụng công thức nguyên hàm, ta có 3 dx   C  . ln 3 2 2
Câu 14. Trong không gian Oxyz , mặt cầu S   x   2 :
1  y   z  2  4 có bán kính bằng A. 4 . B. 2 . C.16 . D. 2 Lời giải Chọn A 2 2
Mặt cầu S   x   2 :
1  y   z  2  4, suy ra bán kính R  4  2 .
Câu 15. Trong không gian Oxyz , đường thẳng vuông góc với mặt phẳng  P : x  y  2z  3  0 có một
vectơ chỉ phương là     A. u       3 0; 1;2.
B. u  1; 2; 3 . C. u  1; 2; 3 .
D. u  1; 1; 2 . 1   2   4   Lời giải Chọn D 
Mặt phẳng  P : x  y  2z  3  0 có VTPT là n  1; 1; 2 . P 
Đường thẳng vuông góc với mặt phẳng P suy ra VTCP của đường thẳng cùng phương với  
VTPT của mặt phẳng  P hay u  kn  k 1; 1; 2 . P  
Chọn k  1 suy ra ta có một VTCP của đường thẳng là u  1; 1; 2 . 1  
Câu 16. Trong không gian Oxyz , cho tứ diện ABCD với A3; 1 
;1 và mặt phẳng  BCD có phương
trình x  2 y  2z  5  0 . Chiều cao AH của tứ diện ABCD bằng 2 1 6 11 A. . B. 2 . C. . D. . 3 3 11 Lời giải Chọn B
Chiều cao của tứ diện ABCD là khoảng cách từ A đến BCD . Trang 9    
Khi đó ta có AH   A BCD 3 2.  1 2.1 5 d ,   2 . 1  2   2  2 2 2
Câu 17. Trong không gian Oxyz , cho hai điểm M 2;1;0 và N 1; 2;  2 . Mặt phẳng  P vuông góc
với MN tại điểm N có phương trình
A. x  y  2z 1  0 .
B. 3x  3y  2z 13  0 .
C. 3x  3y  2z  9  0 .
D. x  y  2z  5  0 . Lời giải Chọn D uuur Ta có MN   1  ;1; 2 . uuur uuur
Do MN  P nên ta chọn P có VTPT n  MN  1;1;2 . P   
Suy ra phương trình P là x 1 y  2  2z  2  0  x  y  2z  5  0 . 4x
Câu 18. Khi tìm nguyên hàm    
x , bằng cách đặt 2 t x
3 ta được nguyên hàm nào sau đây? x  3 d 2 2 2 1 1 4 A. dt  . B. dt  . C. dt  . D. dt  . 2 t 2 t 2 2t 2 t Lời giải Chọn A Đặt 2
t  x  3  dt  2 d
x x  2dt  4 d x x .  4x 2 Vậy ta có     x  t  với 2 t x 3 .  3 d d 2 2 2 t x
Câu 19. Cho số phức z = 4+ 3i và w = 2 + i . Số phức z + w bằng A. 3+ 2i . B. 2 + 4i . C. 6 + 4i . D. 2+ 2i . Lời giải Chọn C Trang 10
Ta có z + w = (4 + 3i)+ (2 + i)= 6 + 4i .
Câu 20. Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số 1 y =
, trục hoành và các đường thẳng 2x + 1
x = 1, x = 2 . Khối tròn xoay tạo thành khi quay (H ) quanh trục hoành có thể tích bằng p 5 1 5 5 A. ln . B. ln . C. p ln . D. p ln15. 2 3 2 3 3 Lời giải Chọn A 2 2 1 p p 5
Thể tích khối tròn xoay cần tính là V = p dx = ln 2x + 1 = ln ò . 2x + 1 2 2 3 1 1
Câu 21. Cho số phức z thoả mãn z + 2z = 12 + 3i . Phần ảo của z bằng A. 3 . B. 4 . C.- 3 . D.- 4 . Lời giải Chọn C
Đặt z = x + yi ( , x y Î ¡ ). Theo đề ìï 3x = 12 ìï x = 4 ï ï
z + 2z = 12 + 3i Û x + yi + 2(x - yi)= 12 + 3i Û 3x- yi = 12+ 3i Û í Û í ï - y = 3 ï y = - 3 ïî ïî
Vậy phần ảo của số phức z là - 3 . 2 Câu 22. Biết ln d
x x  a ln 2  b 
trong đó a, b là các số nguyên. Tính a  b . 1
A. a  b  3.
B. a  b  2  .
C. a  b 1.
D. a  b  2 . Lời giải Chọn C Trang 11  1 u   ln x du  dx Đặt    x . dv  dx v  x 2 2 2 2 1 2 Ta có: ln d
x x  x ln x  . x
dx  2ln 2  dx  2ln 2  x  2ln 2 1    . 1 1 x 1 1 1
Vậy a  2, b  1
  a  b  1.
Câu 23. Hàm số nào sau đây là một nguyên hàm của hàm số    ex f x x ? 2 x A. ex ex x  1 . B. ex x 1 . C. ex 1. D. ex ex x  1. 2 Lời giải Chọn D
Ta có:   d  ex f x x x dx  . u   x du  dx Đặt    .
dv  exdx v  ex
Khi đó:   d  ex  exd  ex ex f x x x x x  C   ex  ex x
1 là một nguyên hàm của hàm    ex f x x .
Câu 24. Cho số phức z thỏa mãn 3  4i z  10 . Môđun của số phức z bằng 5 2 1 A. . B. . C. 2 . D. . 2 5 2 Lời giải Chọn C Trang 12 2 2 10 6 8  6   8 
Ta có: 3  4i z  10  z 
  i  z     2     . 3  4i 5 5  5   5 
Câu 25. Trong không gian Oxyz , đường thẳng đi qua hai điểm A1;0; 2, B 4;1;0 có phương trình tham số là x  3   t x  1   3t x 1 3t x  3 t     A.  y  1  .
B. y  t .
C.  y  t . D. y  1 .     z  2  2t  z  2   2t  z  2  2t  z  2   2t  Lời giải Chọn C 
Ta có AB  3;1;  2 . 
Phương trình đường thẳng AB đi qua điểm A và nhận véctơ AB  3;1; 2 là véctơ chỉ x 1 3t 
phương y  t z  2 2t 
Câu 26. Có tất cả bao nhiêu số phức z thỏa mãn 2
z là số thực và z  2  i  2 ? A.2. B. 1. C. 4. D.3. Lời giải Chọn D
Gọi số phức z  a  bi,  , a b    .
Theo giả thiết có z  a  bi2 2 2 2
 a b  2abi là số thực nên ab  0 . 2 2
Mặt khác z  2  i  2  a  2  b  
1 i  2  a  2  b   1  4 . Trang 13 a  0   b  1  ab  0 b    0  Từ đó, ta có hệ     a 2  2 b 2 1 4      a  2  3   b   0  
a  2  3
Vậy có 3 số phức thỏa mãn yêu cầu bài toán. 1 Câu 27. Cho hàm số 2 y 
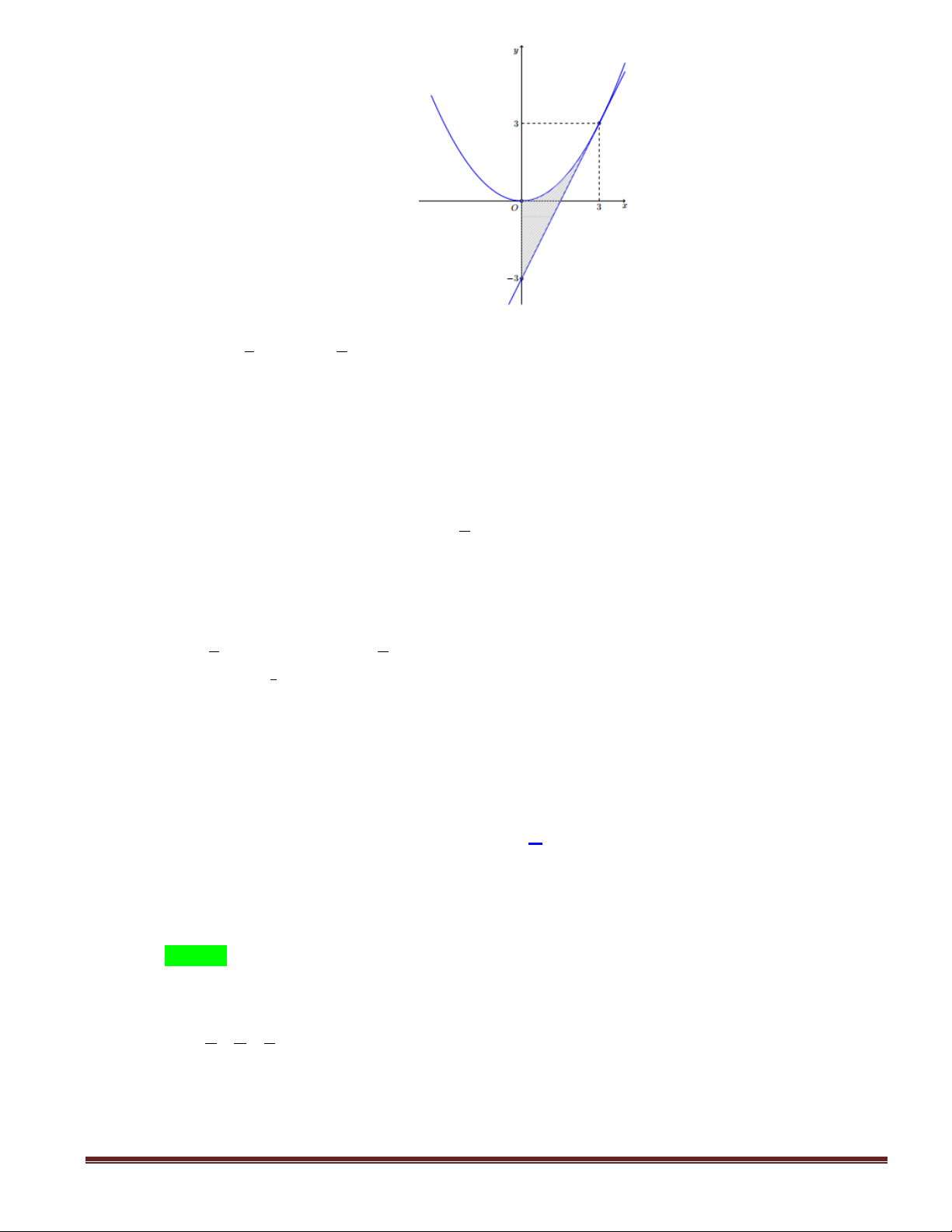
x có đồ thị P và d  là tiếp tuyến với P tại điểm có hoành độ x  3 3
(tham khảo hình vẽ bên).
Diện tích hình phẳng giới hạn bởi  P , d  và trục hoành bằng 3 3 9 A. . B. . C. 3 . D. . 4 8 4 Lời giải Chọn A Trang 14 1 2 Ta có 2 y  x  y '  x . 3 3 x  3 0 
Phương trình tiếp tuyến d biết y  3
là y  2 x  3  3  y  2x  3. 0  f '  3  2 Giao điể 3
m của d với trục hoành là x  . 2
Từ hình vẽ ta thấy, diện tích hình phẳng giới hạn bởi  P , d  và trục hoành là 3 3 1 3 2 S 
x dx  2x  3 dx    . 3 4 0 3 2
Câu 28. Trong không gian Oxyz cho mặt phẳng  P vuông góc với mặt phẳng Q : 2x  y  z  0 và
cắt các trục Ox, Oy, Oz lần lượt tại A2;0;0, B 0; ;
b 0,C 0;0;c với b  0, c  0 sao cho thể tích khối tứ diện .
O ABC bằng 3 . Giá trị b  c bằng A. 6  . B. 9  . C. 9 . D. 6 . Lời giải Chọn D
Do mặt phẳng  P cắt các trục Ox,Oy,Oz lần lượt tại A2;0;0, B 0; ;
b 0,C 0;0;c nên   x y z P :
   1  bcx  2cy  2bz  2bc  0 . 2 b c 
Khi đó P có véc tơ pháp tuyến là: n  b ; c 2 ; c 2b . P    Trang 15 
Mặt phẳng Q có véc tơ pháp tuyến là: n  2;1;    1 . Q  
Vì P  Q   n . 
n   0  2bc  2c  2b  0  bc  c  b  0 (1). P Q 1 2bc bc bc Ta có V  . OA . OB OC   . Theo bài ra thì V  3   3  bc  9 . O. ABC O. ABC 6 6 3 3
Từ (1) suy ra 9  c b  0  b  c  9 .
Câu 29. Cho số phức z thỏa mãn z  2iz  4 là số thuần ảo. Trên mặt phẳng tọa độ , tập hợp điểm
biểu diễn số phức z là đường tròn có bán kính bằng A. 3 . B. 5 . C. 5 . D. 3 . Lời giải Chọn C
Đặt z  x  yi,x, y   .
Ta có z  2iz  4  x  y  2i 
 x  4  yi    
 xx  4  y y  2  xy  
x 4y 2i .
Khi đó z  2iz  4là số thuần ảo  xx  4  y y  2  0
 x  y  x  y   x  2   y  2 2 2 4 2 0 2 1  5.
Vậy tập hợp điểm biểu diễn số phức z là đường tròn có bán kính là R  5 .
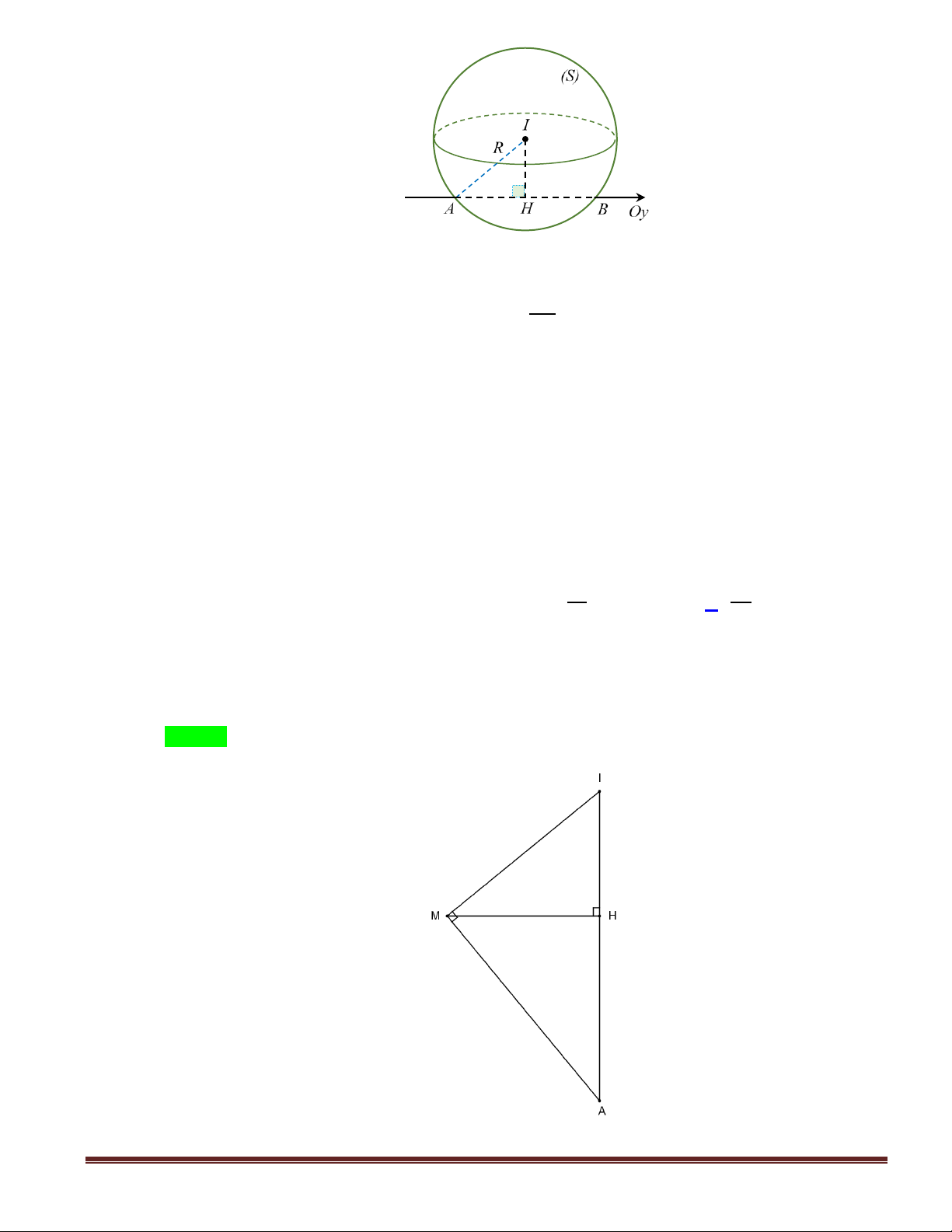
Câu 30. Trong không gian Oxyz , cho mặt cầu S  có tâm I 1;  2;3 và cắt trục Oy tại hai điểm A , B
sao cho AB  4 . Phương trình mặt cầu S  là: 2 2 2 2 2 2 A.  x  
1   y  2   z  3  10. B.  x  
1   y  2   z  3  6 . 2 2 2 2 2 2 C.  x  
1   y  2   z  3  8 . D.  x  
1   y  2   z  3  14. Lời giải Chọn D Trang 16
 Gọi H là hình chiếu của tâm I lên trục Oy : H 0; 2  ;0  2 IH  10 . 2    AB
Bán kính mặt cầu S  là: 2 2 2 2
R  AH  IH   IH 14   .  2   2 2 2
Phương trình mặt cầu S  là: S    x  
1   y  2   z  3  14 .
Câu 31. Trong không gian Oxyz , cho mặt phẳng  P : 2x  y  2z 1  0 ; điểm A5;1; 4 và mặt
cầu S  có tâm I a ;b;c cắt mặt phẳng  P theo giao tuyến là đường tròn C có bán kính
r  2 . Biết rằng mọi điểm M thuộc C thì AM là tiếp tuyến của S  . Giá trị của a  b  c bằng: 20 20 A. 3 . B. 3  . C.  . D. . 9 9 Lời giải Chọn D Trang 17 2.5 1 2. 4  1
Ta có: d  d  A; P     6 . 2 2 2 2 1  2
Do mọi điểm M thuộc C thì AM là tiếp tuyến của S  nên M thuộc mặt cầu tâm A . Mặt
cầu này cắt mặt cầu S  theo giao là đường tròn C nên hình chiếu của A và I trên mặt
phẳng  P đều là tâm H của đường tròn C .
Do AM là tiếp tuyến của S  nên A và I nằm khác phía so với mặt phẳng  P và tam giác 2 2 HM r 2 1  
MAI vuông tại M nên 2 H .
A HI  HM  HI     HA  1 HI  AH . HA d 3 9 9 
Mặt phẳng  P có một vector pháp tuyến n  2; 1;  2 
Do AH   P nên AH có một vector chỉ phương là n  2; 1;  2
x  5  2t  
Phương trình AH : y  1   t z  4   2t 
x  5  2t t   2    y  1   t x 1
Do H  AH   P nên tọa độ H thỏa mãn hệ:    z  4   2t  y  1 
2x  y  2z 1 0 z  0    11 4 H 1;1;0  5 11 4 I ; ;    5 a  ; b  ; c   20
a  b  c  .  9 9 9  9 9 9 9
Câu 32. Cho hàm số y  f  x có đạo hàm liên tục trên 0;   , thỏa mãn  ex. ex   ex x f f 1
với mọi x  và f  
1  1. Giá trị f 4 thuộc khoảng nào sau đây? A. 3; 4 . B. 2;3 . C. 4;5 . D. 5;6 . Lời giải Chọn D     
Ta có:  ex. ex   ex x f f
1  exe x ex 1 e x f f x  e x 
ex 1 e x f x  ln 4 ln 4 ln 4    ln 4 ex  x x x 
ex d   1 ex f x x dx   e f  e 
 1 xe dx   0 0 0 0 ln 4  1 4    1  1  ex f f x dx . 4 0 u  1 x  u   x Đặt   d d 
dv  exdx
v  ex Trang 18 ln 4  1  1 1 4    1   1  ln 4 ex   ex f f x dx     4 1 1 ln4 ln 4 1 e x f        4 0 4 4 0 0
 f 4  4  ln 4  5,395;6. Trang 19

Đề Thi Toán 12 Học Kỳ 2 Quảng Nam 2020-2021 Có Đáp Án Và Lời Giải Chi Tiết

Thông tin :

Tài liệu liên quan:

Đề chính thức kỳ thi tốt nghiệp THPT năm 2024 môn Toán

Đề kiểm tra Toán 12 năm 2024 – 2025 trường THCS&THPT Nguyễn Khuyến – TP HCM (13/09/2024)

Đề kiểm tra Toán 12 năm 2024 – 2025 trường Nguyễn Khuyến & Lê Thánh Tông – TP HCM (22/09/2024)

Đề kiểm tra Toán 12 năm 2024 – 2025 trường Nguyễn Khuyến & Lê Thánh Tông – TP HCM (06/10/2024)

Đề thi thử TN THPT môn Toán đợt tháng 6 năm 2024 cụm trường THPT – Bắc Ninh