Đề Thi Tuyển Sinh 10 Môn Toán Chung Sở GD Hòa Bình 2025-2026 Có Đáp Án

SỞ GD&ĐT HÒA BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG ĐỀ THI MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho tất cả các thí sinh)
Thời gian làm bài: 120 phút, không kể thời gian giao đề.
Đề thi có 01 trang, gồm 05 câu.
Câu I (3,5 điểm)
1. Tìm điều kiện của x để biểu thức x − 2 có nghĩa.
2. Tính giá trị biểu thức: A = 36 + 9
3. Giải các phương trình: a) 2x +1 = 5 b) 2
x + 2x − 3 = 0
4. Trong mặt phẳng tọa độ Oxy cho đường thẳng (d ) : y = x + 3.
a) Vẽ đường thẳng (d ) .
b) Tìm giá trị của m để đường thẳng (d ') : y = 2x + m −1 cắt đường thẳng (d ) tại
một điểm trên trục tung.
Câu II (1,5 điểm) 2x + y = 3
1. Giải hệ phương trình: 
x − 2y = −1
2. Cho tam giác ABC vuông tại A , đường cao AH ( H  BC ), biết BH = 4cm,
HC = 9cm . Tính độ dài đoạn thẳng AH .
Câu III (2,0 điểm) 1. Cho phương trình: 2
x − 8x + m −1 = 0 (m là tham số). Tìm giá trị của m để phương
trình có hai nghiệm x , x
P = (x −1)(x −1) + 2087 1 2 sao cho biểu thức 2 2
đạt giá trị nhỏ nhất. 1 2
2. Một đội xe dự định chở 120 tấn xi măng vào công trường. Khi chuẩn bị khởi hành
thì đội xe được bổ sung thêm 5 chiếc xe nữa, nên cả đội đã chở thêm được 5 tấn và mỗi xe
chở ít hơn so với dự định là 1 tấn xi măng. Hỏi theo dự định đội xe có bao nhiêu chiếc xe?
Biết khối lượng xi măng mỗi xe chở là như nhau và mỗi xe chỉ chở đúng một chuyến.
Câu IV (2,0 điểm)
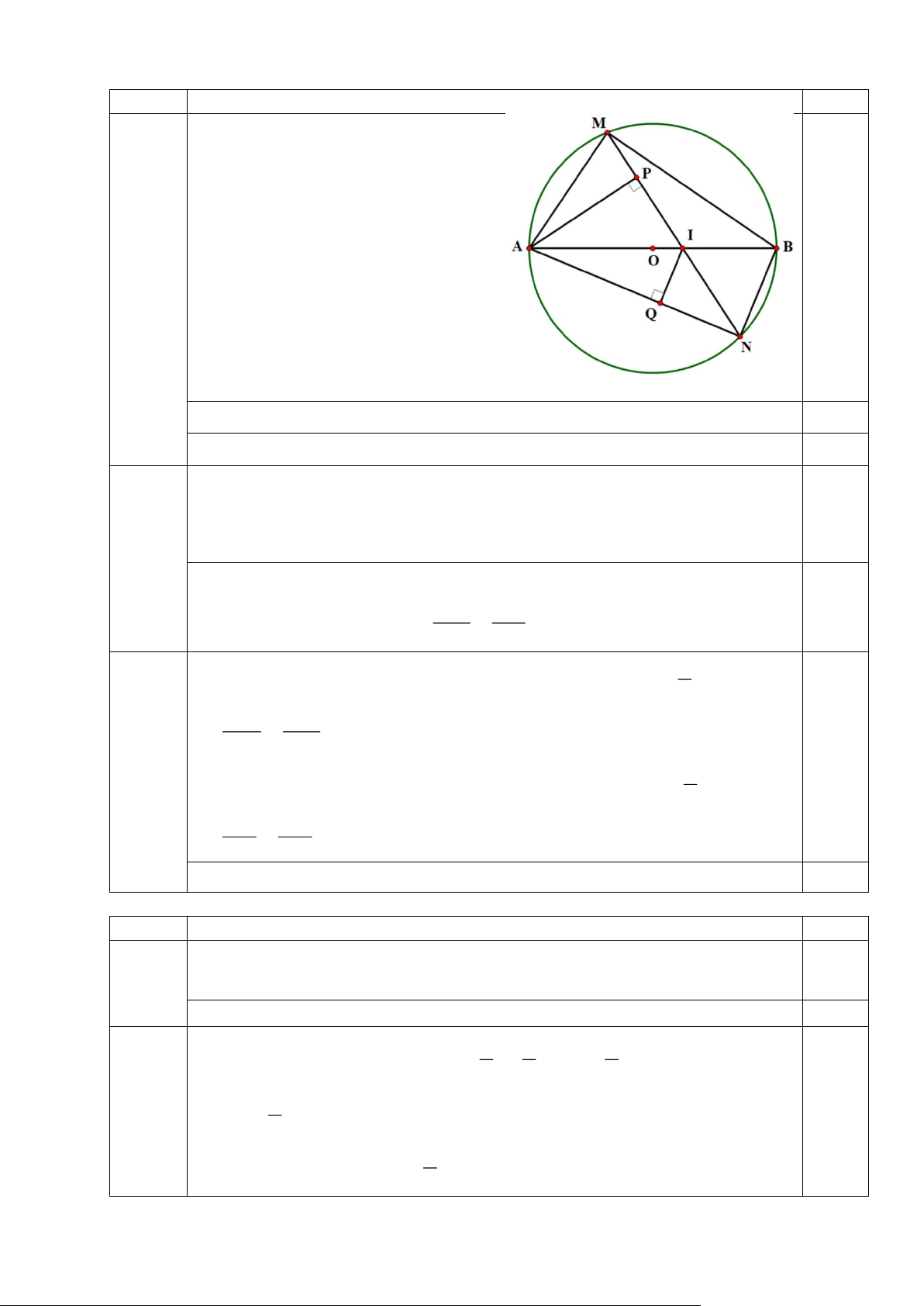
Cho đường tròn (O; R) có đường kính AB . Lấy điểm I bất kỳ thuộc đoạn thẳng
AB ( I khác A và B ). Qua I kẻ một đường thẳng d bất kỳ cắt đường tròn (O) tại M và
N sao cho AM  AN ( M khác A và B ; N khác A và B ). Từ A kẻ AP vuông góc với
MN tại P , từ I kẻ IQ vuông góc với AN tại .
Q Chứng minh rằng:
a) Tứ giác APIQ là tứ giác nội tiếp.
b) PM .AI = M . A QI. c) 2
AM .BN + AN.BM  4R .
Câu V (1,0 điểm)
1. Tìm nghiệm nguyên của phương trình: 2 2
2x + 3xy + y + 5x + 3y = 11.
2. Cho a,b là các số thực thỏa mãn 2 2
4a − 2ab + b = 4a + 2b .
Tìm giá trị lớn nhất của biểu thức P = 253(2a + b) .
-------- HẾT --------
Họ và tên thí sinh: .......................................... Số báo danh: ...................... Phòng thi: ........
Giám thị 1: .................................................... Giám thị 2: ..................................................... Trang 1 SỞ GD & ĐT HOÀ BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 ĐỀ CHÍ NH THỨC HƯỚNG
DẪN CHẤM MÔN TOÁN
(Dành cho tất cả các thí sinh)
(Hướng dẫn chấm này gồm có 02 trang)
Câu I (3,5 điểm) Phần, ý Nội dung Điểm 1
x − 2 có nghĩa khi x − 2  0  x  2. 0,5 2 36 + 9 = 6 + 3 = 9 0,5 3a Tìm được x = 2 0,5 3b
Tìm đúng 2 nghiệm x = 1; x = −3 1 2 0,5
Xác định được 2 điểm thuộc đồ thị. 0,5 Vẽ đúng đồ thị: 4a 0,5
(d ') : y = 2x + m −1 cắt đường thẳng (d ) tại một điểm trên trục tung 4b  0,5
m −1 = 3  m = 4 .
Câu II (1,5 điểm) Phần, ý Nội dung Điểm 1
Tìm được nghiệm (x;y) = (1;1). 1,0 2 2 AH = H .
B HC = 4.9 = 36  AH = 6 (cm) 0,5
Câu III (2,0 điểm) Phần, ý Nội dung Điểm '
 = 16 − (m −1) = 17 − m 0,25
Phương trình đã cho có hai nghiệm khi và chỉ khi '
  0  m  17 0,25 1
Áp dụng hệ thức Viet, ta có: x + x = 8; x x = m −1 1 2 1 2 0,25 2 2 2 2 2
P = (x x ) − x − x + 2088 = (x x ) − (x + x ) + 2x x + 2088 1 2 1 2 1 2 1 2 1 2 2 2 2
= (m −1) − 8 + 2(m −1) + 2088 = m + 2023  2023. 0,25
Dấu "=" xảy ra khi và chỉ khi m = 0 (TM )
Gọi số chiếc xe ban đầu của đội xe là x ( * x  N )  120
Số tấn xi măng mỗi xe phải chở theo dự định là: (tấn). 0,25 x 120 125 2
Lập được phương trình: = +1 0,25 x x + 5
Giải phương trình tìm được x = 20 (TM ); x = −30 (KTM ) 1 2 0,5 KL: … Trang 2
Câu III (2,0 điểm) Phần, ý Nội dung Điểm a
* Ghi chú: Nếu HS chỉ vẽ hình thì cho 0,25 điểm. Ta có: API = AQI = 90 (  gt) 0,5
 API + AQI = 90 + 90 = 180  tứ giác APIQ nội tiếp được. 0,5 Ta có: 90o ANB =
(góc nội tiếp chắn nửa đường tròn)
 BN^ AN , mà IQ^ AN  IQ / / BN  ABN = AIQ (đồng vị) 0,25
Mà ABN = AMP (2 góc nội tiếp cùng chắn cung AN)  AIQ = AMP b
Xét ° PMA và ° QIA, có: = = 90o APM AQI
; AIQ = AMP (cmt) 0,25  PM MA
° PMA ” ° QIA (g.g)  =
 PM.AI = M . A QI. QI IA 1
• ° APM ” ° ANB ( = = 90o APM ANB
; AMP = ABN = sđ AN ) 2 AM PM  =
 AM .BN = A . B PM (1) AB NB 0,25 c 1
• ° APN ” ° AMB ( = = 90o APN AMB
; ANM = ABM = sđ AM 2 AN PN  =
 AN.MB = A . B PN (2) AB MB Từ (1) và (2) 2
 AM.BN + AN.BM = A . B PM + A .
B PN = AB.MN  4R . 0,25
Câu IV (1,0 điểm) Phần Nội dung Điểm 2 2
2x + 3xy + y + 5x + 3y = 11 0,25 1
 (x + y + 2)(2x + y +1) =13
Vì x, y nguyên nên (x;y) = (13; –14); (–12; 23); (–11; 8); (13; –28) 0,25 2 b b b 2 2 2 4a 2ab b 4a + 2b a − . a +   − + =    = a + 2  2  2 b 2 Đặt m = , ta có 2 2
a − am + m = a + m ( ) 1 và 0,25 2  b 
P = 253(2a + b) = 506a +  = 506(a + m)  2  Trang 3
( )  (a + m)2 − am = a + m  (a + m)2 1 3
= (a + m) + 3am . a + m
Chứng minh được (a + m) ( )2
2  4am  am  . 4 Suy ra
(a + m)2 = (a + m) + am  (a + m) 3 + (a + m)2 1 3
 (a + m)2  a + m 4 4 0,25  (a + m) (
 a + m)− 4  0  0  a + m  4.
Do đó 0  P  4.506  0  P  2024 . a = 2
Vậy max P = 2024  a = m = 2   . b  = 4
* Chú ý: Mọi cách giải khác đúng đều được xem xét và cho điểm tối đa.
-------- Hết -------- Trang 4