Đề Thi Tuyển Sinh 10 Môn Toán Chuyên Tin Sở GD Hòa Bình 2025-2026 Có Đáp Án

SỞ GD&ĐT HÒA BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG ĐỀ THI MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho thí sinh dự thi vào lớp chuyên Tin) THUC
Thời gian làm bài: 150 phút, không kể thời gian giao đề.
Đề thi có 01 trang, gồm 04 câu.
Câu I (3,0 điểm) 2 x − 4
1. Rút gọn biểu thức: A = x − 2
2. Tính giá trị biểu thức: B = 4 + 2 3 + 4 − 2 3
3. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d): y = ax + b . Tìm a và b để
đường thẳng (d ) đi qua hai điểm (
A 1;3) và B(2;5).
Câu II (3,0 điểm)
x(y −1) + y(x +1) = 6
1. Giải hệ phương trình:  (
 x −1)(y +1) = 2 2. Cho phương trình: 2 2
x − 3mx + m − 5 = 0 ( m là tham số). Tìm m để phương trình
có hai nghiệm x ; x thỏa mãn: 2
x + 3mx −13  0 . 1 2 1 2 3. Giải phương trình: 2 2 2
(x − 6x) + (x − 3) = 29 .
Câu III (3,0 điểm)
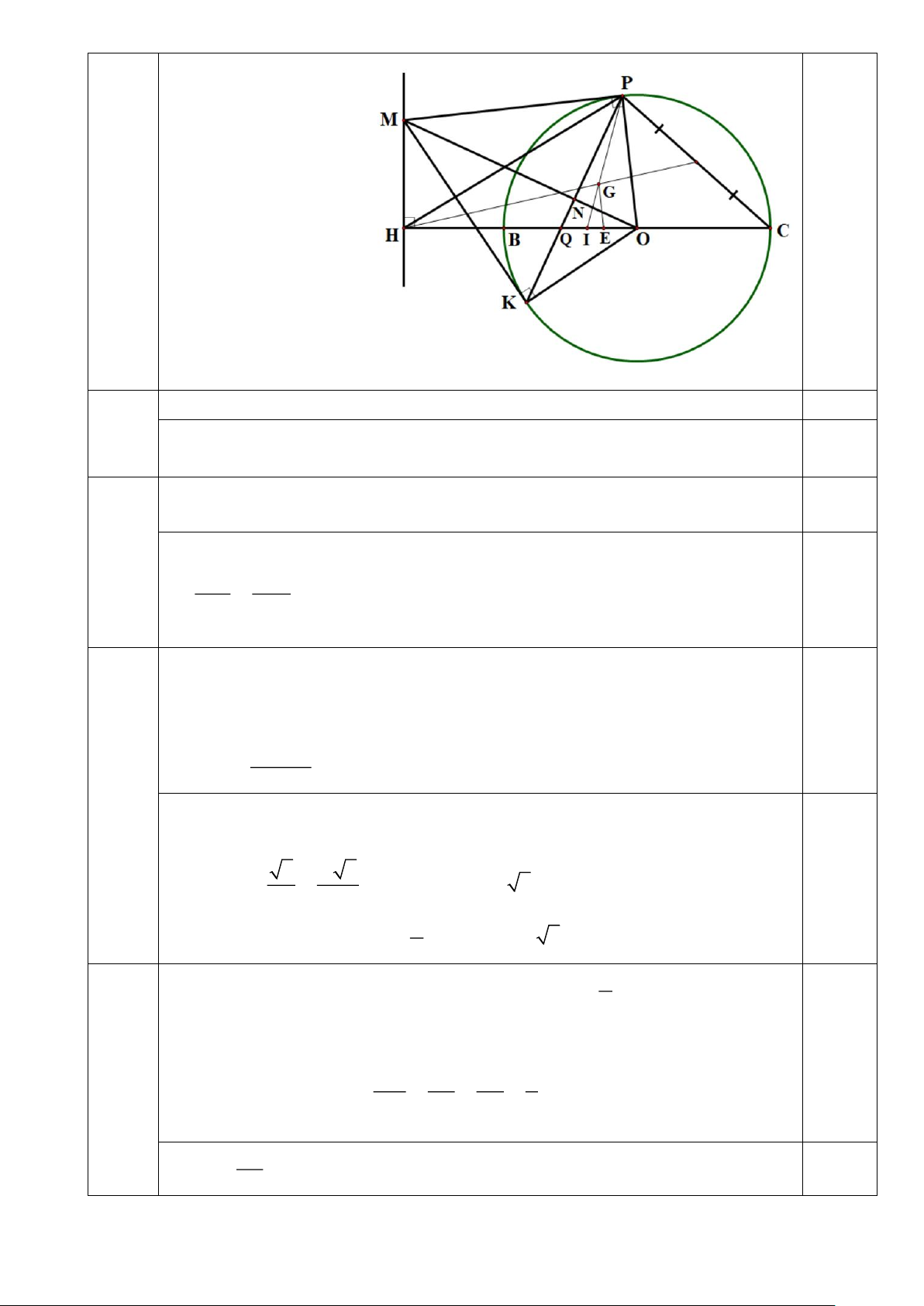
Cho đường tròn (O; R) đường kính BC, điểm H cố định thuộc tia đối của tia BC.
Qua H kẻ đường thẳng d vuông góc với BC. Lấy điểm M bất kì trên đường thẳng d ,
qua M kẻ các tiếp tuyến MP, MK với đường tròn (O) . Dây PK cắt OM tại N và cắt OH tại . Q
1. Chứng minh năm điểm M , P, O, K, H cùng thuộc một đường tròn. 2. Chứng minh rằng 2
OH.OQ = R . 3. Cho 0
POK = 120 . Tính diện tích tứ giác MPOK theo R.
4. Chứng minh rằng khi điểm M di chuyển trên đường thẳng d thì trọng tâm G của
tam giác HPC chạy trên một đường tròn cố định.
Câu IV (1,0 điểm)
1. Kết thúc năm học 2022 - 2023, Hòa hỏi Bình: “Bạn có bao nhiêu bài kiểm tra đạt
điểm 8 và điểm 9 vậy?”. Bình trả lời: “Số bài kiểm tra đạt điểm 8, điểm 9 của tớ nhiều hơn
21 và tổng số điểm của các bài kiểm tra đó là 183”. Em hãy tính giúp Hòa xem Bình có bao
nhiêu bài kiểm tra đạt điểm 8 và bao nhiêu bài kiểm tra đạt điểm 9 nhé. 2023 1
2. Tìm giá trị nhỏ nhất của biểu thức P =
+ , với 0  x  1. 1− x x
------------- HẾT --------------
Họ và tên thí sinh: ................................................ Số báo danh: ............................ Phòng thi: .......
Giám thị 1: ....................................................... Giám thị 2: ............................................................. Trang 0
SỞ GD&ĐT HÒA BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
HƯỚNG DẪN CHẤM MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho thí sinh dự thi vào lớp chuyên Tin) THUC
Hướng dẫn chấm gồm có 03 trang
Câu I (3,0 điểm) Phần, Nội dung Điểm ý * ĐKXĐ: x  2 1 2 x − 4 (x − 2)(x + 2) A = = = x + 2 1,0 x − 2 x − 2 2 2
A = 4 + 2 3 + 4 − 2 3 = ( 3 +1) + ( 3 −1) 0,5 2 = 3 +1+ 3 −1 = 2 3. 0,5 a  + b = 3 3
(d ) đi qua hai điểm (
A 1;3) và B(2; ) 5   0,5 2  a + b = 5
Giải hệ phương trình ta được: a = 2; b = 1. KL…. 0,5
Câu II (3,0 điểm) Phần, Nội dung Điểm ý
x(y −1) + y(x +1) = 6 2
 xy − (x − y) = 6 xy = 3      0,5 (
 x −1)(y +1) = 2
xy + (x − y) = 3 x − y = 0 1 2 x = 3   . x = y 0,5
Tìm được các nghiệm: ( 3; 3); (− 3;− 3) Ta có 2 2 2
 = 9m − 4(m − 5) = 5m + 20  0, m .
Suy ra phương trình luôn có 2 nghiệm phân biệt với mọi m .
x + x = 3m 0,5
Theo hệ thức Vi-ét ta có: 1 2  2
x .x = m − 5 1 2 2 2 2 2
x + 3mx −13  0  x + (x + x )x −13  0  (x + x ) − x .x −13  0 1 2 1 1 2 2 1 2 1 2 0,5 2 2 2
 (3m) − (m − 5) −13  0  8m  8  −1  m  1 2 2 2 2 2 2
(x − 6x) + (x − 3) = 29  (x − 6x) + (x − 6x) − 20 = 0 (1) 0,25 t  = 4 Đặt 2
t = x − 6x, phương trình (1) trở thành: 2
t + t − 20 = 0  0,25 t   = −5 3 x = 3 + 13 2 2
 t = 4  x − 6x = 4  x − 6x − 4 = 0   0,25 x = 3 − 13 x =1 2 2
 t = −5  x − 6x = −5  x − 6x + 5 = 0   x = 5 0,25 Kết luận: …
Câu III (3,0 điểm) Phần, Nội dung Điểm ý
* Ghi chú: Nếu HS lấy điểm H thuộc tia BC thì trừ 0,5 điểm toàn bài. Giải thích được: = = = 90o MPO MHO MKO 0,5 1
 P, K, H thuộc đường tròn đường kính . MO
 M , P, O, K, H 0,5
cùng thuộc đường tròn đường kính . MO
Xét MPO vuông tại P, có PN ⊥ MO:  2
ON OM = OP (1) (Hệ thức lượng trong tam giác vuông). 0,5
ONQ ” OHM ( HOM chung; ONQ = OHM = 90 )  . 2  ON OQ =
 OM ON = OH OQ (2) 0,5 OH OM Từ (1), (2)  2 2
OH OQ = OM ON = OP = R . Vì 120o POK =
nên PMK = 60 và MO là phân giác của PMK
 PMO = KMO = 30
OPM vuông tại P, có: OP = OM . Sin PMO 0,25  R = = OM 2R (cm). sin 30
PNO vuông tại N , có: NP = OP.sin PON 3
mà PON = 90 − OMP = 90 − 30 = 60 (MPO vuông tại P).  3 R 3 NP = R  =
(cm)  KP = R 3 (cm) 0,25 2 2 1 Ta có 2
OM ⊥ KP  S = OM KP = R (cm2). MPOK . 3 2 4 2
Lấy I là trung điểm của HC , G  PI sao cho PG = PI. 3
Từ G kẻ đường thẳng song song với OP cắt HC tại E .
HC cố định  I cố định 0,25 GE IE IG 1
° IPO có GE // PO  = =
= (Định lí talet) (do G là trọng PO IO IP 3 tâm của PHC).  IO IE =
không đổi. Mà I, O cố định  E cố định. (1) 0,25 3 Trang 1 PO R GE = = không đổi. (2) 3 3  R 
(1), (2)  G  E;
 cố định khi M chuyển động trên d .  3 
Câu IV (1,0 điểm) Phần, Nội dung Điểm ý
Gọi số bài điểm 8 và điểm 9 của Bình đạt được lần lượt là x, y (bài)( * x, y  ) .
Theo giả thiết x + y  21.
Tổng số điểm của tất cả các bài kiểm tra đó là 183 nên ta có: 8x + 9 y = 183. 0,25 Ta có
= x + y  (x + y) 183 183 8 9 8  x + y  . 1 8 183 Do * x + y 
và 21  x + y 
nên x + y = 22 . 8 x + y = 22 x =15 Ta có hệ    (thỏa mãn). 8  x + 9y =183 y = 7 0,25
Vậy Bình được 15 bài điểm 8 và 7 bài điểm 9. 2023 1 (2023 − 2023 ) x + 2023x (1− ) x + x Ta có P = + = + 1− x x 1− x x 2023x 1− x 2023x 1− x = 2024 + +  2024 + 2  = 2024 + 2 2023 0,25 1− x x 1− x x
(áp dụng BĐT Côsi với 2 số dương) 2 2023x 1− x 1 Đẳng thức xảy ra =
 2023x = (1− x)2 2  x = 1− x x 2023 +1 1 (loại nghiệm x = ) 0,25 1− 2023 1
Vậy giá trị nhỏ nhất của P bằng 2024 + 2 2023 khi x = . 2023 +1
* Chú ý: Các lời giải đúng khác đều được xem xét cho điểm tương ứng.
-------- HẾT -------- Trang 2