Đề Thi Tuyển Sinh 10 Môn Toán Sở GD Kon Tum 2025-2026 Có Lời Giải

SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 KON TUM
Môn: TOÁN (chung)
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Câu 1. (3,0 điểm)
a) Rút gọn biểu thức A = 9 − 2 .
b) Giải phương trình 2x − 6 = 0 . c) Cho hàm số 2
y = f (x) = 3x . Tính giá trị của hàm số tại x = 2 . Câu 2.
(2,0 điểm) Không sử dụng máy tính cầm tay, hãy giải phương trình và hệ phương trình sau: a) 2
x + 3x − 4 = 0 ; x + 2y = 5 b)  . 3  x − 2y = 7 Câu 3.
(1,0 điểm) Một nhóm gồm 15 học sinh (cả nam và nữ) tham gia buổi lao động trồng cây. Các
bạn nam trồng được 54 cây, các bạn nữ trồng được 30 cây. Mỗi bạn nam trồng được số cây
như nhau và mỗi bạn nữ trồng được số cây như nhau. Tính số học sinh nam và số học sinh nữ
của nhóm, biết rằng mỗi bạn nam trồng được nhiều hơn mỗi bạn nữ 1 cây. Câu 4.
(1,0 điểm) Trong mặt phẳng tọa dộ Oxy , cho parabol 2
(P) : y = x và đường thẳng
(d ) : y = 3x + m . Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt
A( x ; y , B x ; y thỏa mãn hệ thức x + y = x + y + 4 . 1 1 ) ( 2 2) 1 1 2 2 Câu 5.
(2,5 điểm) Cho đường tròn tâm O và một điểm M nằm ngoài đường tròn đó. Kẻ các tiếp
tuyến MA, MB với đường tròn (O) ( ,
A B là các tiếp điểm). Vẽ đường kính BC của đường
tròn (O) . Gọi H là giao điểm của MO và AB , I là giao điểm thứ hai của đường thẳng MC
và đường tròn (O) , AI kéo dài cắt MO tại K .
a) Chứng minh tứ giác MAOB là một tứ giác nội tiếp.
b) Chứng minh AK vuông góc với IH .
c) Cho biết BC = 2AC = 8 cm . Tính độ dài đoạn thẳng MK .
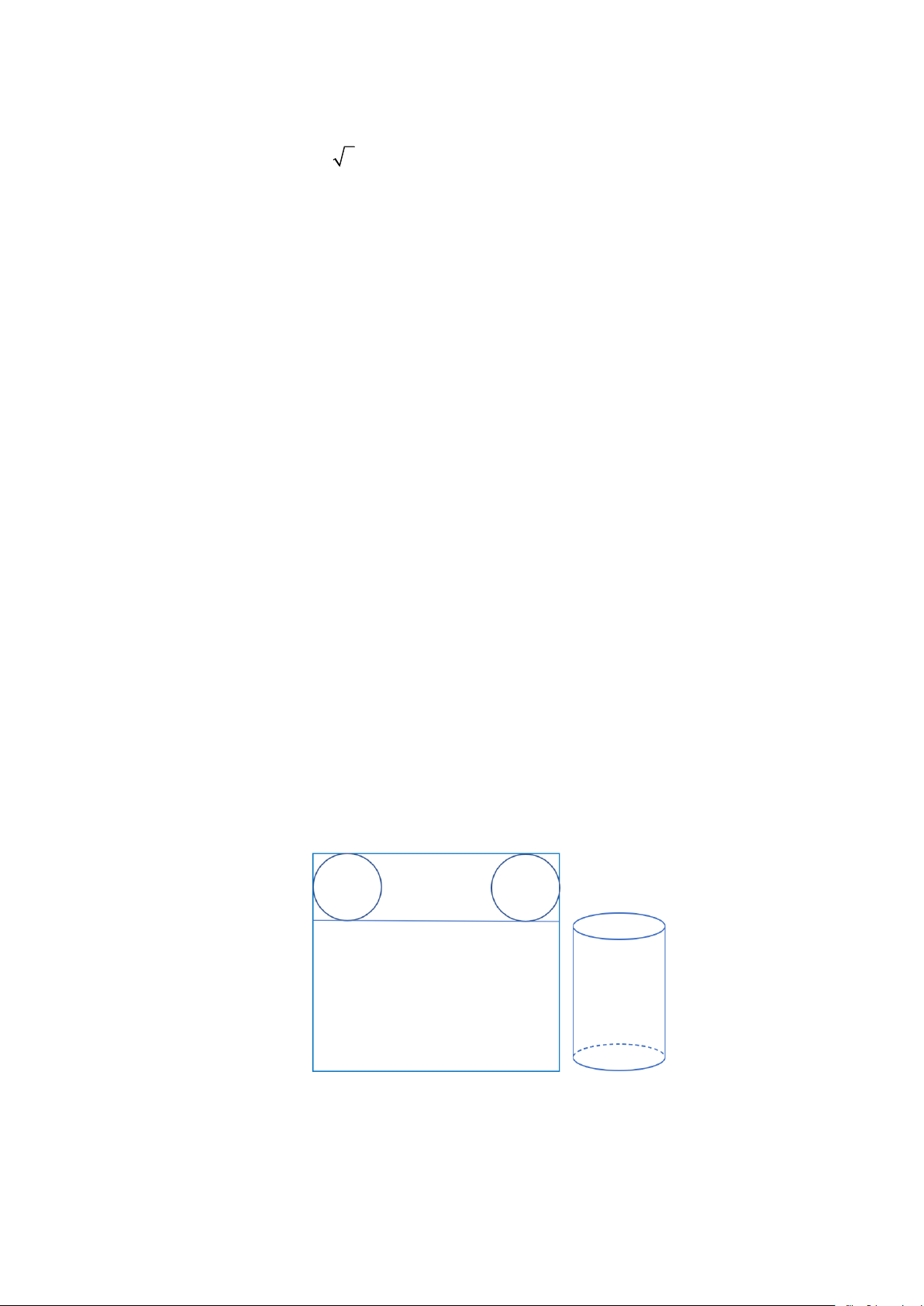
Câu 6. (0,5 điểm) Bạn Nam cắt một tấm bìa hình vuông cạnh 50 cm để được một hình chữ nhật và hai
hình tròn (như Hình 1). Bạn ấy cuộn tròn hình chữ nhật và dán hai mép giấy lại với nhau. Bạn ấy
dán tiếp hai hình tròn vào hai đầu để tạo thành một cái hộp hình trụ có nắp (như Hình 2).
Tính chiều cao của cái hộp tạo thành, biết chiều cao đó nhỏ hơn 50 cm , các mép dán không đáng kể. Hình 1 Hình 2
---------------------------------@Hết@--------------------------------- Trang 1 HƯỚNG DẪN GIẢI Câu 1. (3,0 điểm)
a) Rút gọn biểu thức A = 9 − 2 .
b) Giải phương trình 2x − 6 = 0 . c) Cho hàm số 2
y = f (x) = 3x . Tính giá trị của hàm số tại x = 2 . Lời giải a) A = 9 − 2. = 3− 2 = 1.
b) 2x − 6 = 0  2x = 6.  x = 3.
Vậy phương trình có một nghiệm là x = 3 . c) f ( ) 2 2 = 3.2 = 12 Câu 2.
(2,0 điểm) Không sử dụng máy tính cầm tay, hãy giải phương trình và hệ phương trình sau: a) 2
x + 3x − 4 = 0 ; x + 2y = 5 b)  . 3  x − 2y = 7 Lời giải a) 2
x + 3x − 4 = 0.
Vì a + b + c = 1+ 3+ ( 4 − ) = 0
Nên phương trình có hai nghiệm là x = 1 ; x = 4 − . 1 2 x + 2y = 5 4x = 12 b)    3  x − 2y = 7 x + 2y = 5 x = 3   3  + 2y = 5 x = 3   . y = 1
Vậy hệ phương trình có một nghiệm là (x ; y) = (3 ; ) 1 . Câu 3.
(1,0 điểm) Một nhóm gồm 15 học sinh (cả nam và nữ) tham gia buổi lao động trồng cây. Các
bạn nam trồng được 54 cây, các bạn nữ trồng được 30 cây. Mỗi bạn nam trồng được số cây
như nhau và mỗi bạn nữ trồng được số cây như nhau. Tính số học sinh nam và số học sinh nữ
của nhóm, biết rằng mỗi bạn nam trồng được nhiều hơn mỗi bạn nữ 1 cây. Lời giải
Số học sinh nữ là 15− x (học sinh) * (ÑK : x ; x  15) 54
Số cây mỗi bạn nam trồng được là . x 30
Số cây mỗi bạn nữ trồng được là . 15− x
Vì mỗi bạn nam trồng được nhiều hơn mỗi bạn nữ 1cây nên ta 54 30 có phương trình − = 1 x 15− x
 54(15− x) −30x = x(15− x) 2
 x − 99x + 810 = 0.
Giải ra ta được x = 9 ; x = 90 .
Kết hợp điều kiện ta được số bạn nam là 9 , số bạn nữ là 6 . Trang 2 Câu 4.
(1,0 điểm) Trong mặt phẳng tọa dộ Oxy , cho parabol 2
(P) : y = x và đường thẳng
(d ) : y = 3x + m . Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt
A( x ; y , B x ; y thỏa mãn hệ thức x + y = x + y + 4 . 1 1 ) ( 2 2) 1 1 2 2 Lời giải
Phương trình hoành độ giao điểm của (P) và (d) 2 2
x = 3x + m  x − 3x − m = 0
(d)cắt (P)tại hai điểm phân biệt khi phương trình ( )1có 2 nghiệm phân biệt.Điều này xảy ra khi 9
  0  9+ 4m 0  m − . 4
Vì x , x là hai nghiệm của phương trình ( ) 1 nên 1 2 x + x = 3 2  1 2 ( )  . x x = −m 3  1 2 ( ) Vì ,
A B d nên y = 3x + ;
m y = 3x + m. 1 1 2 2
Khi đó x + y = x + y + 4  x + 3x + m = x + 3x + m + 4  x − x = 1. 1 1 2 2 1 ( 1 ) 2 ( 2 ) 1 2 x = 2
Kết hợp với (2) ta được 1  . x = 1  2 Kết hợp với ( )
3 ta được m = −2(thỏa mãn điều kiện).
Vậy m = −2 là giá trị cần tìm. Câu 5.
Cho đường tròn tâm O và một điểm M nằm ngoài đường tròn đó. Kẻ các tiếp tuyến MA, MB
với đường tròn (O) ( ,
A B là các tiếp điểm). Vẽ đường kính BC của đường tròn (O) . Gọi H
là giao điểm của MO và AB , I là giao điểm thứ hai của đường thẳng MC và đường tròn (O)
, AI kéo dài cắt MO tại K .
a) Chứng minh tứ giác MAOB là một tứ giác nội tiếp.
b) Chứng minh AK vuông góc với IH .
c) Cho biết BC = 2AC = 8 cm . Tính độ dài đoạn thẳng MK . Lời giải A C I O M K H B
a) Chứng minh tứ giác MAOB là một tứ giác nội tiếp. Vì M ,
A MB là các tiếp tuyến của đường tròn (O) nên MA ⊥ AO và MB ⊥ BO
Vì MAO + MBO = 90 + 90 = 180
Nên tứ giác MAOB nội tiếp đường tròn.
b) Chứng minh AK vuông góc với IH . Trang 3
Hai tam giác MIA và MAC đồng dạng vì có M chung và MAI = MCA (cuø ng chaén AI ) MA MI Do đó 2 =  MA = M . C MI ( ) 1 MC MA
Mặt khác vì MA = MB(tính chaát tieáp tuyeán) và OA = OB = R nên MO là đường trung
trực của đoạn thẳng AB.
Vì AH là đường cao của tam giác vuông MAO nên 2
MA = MH.MO (2) MI MO Từ ( ) 1 và (2) suy ra .
MC MI = MH.MO  =  MI  H ∽ MO  C MH MC  MIH = MCO
Mà MCO = IAB (cuøng chaén IB) nên MHI = IAB
Ta lại có IAB + IKH = 90 (
 Do AH ⊥ M ) O
Nên MHI + IKH = 90 hay AK ⊥ IH.
c) Cho biết BC = 2AC = 8 cm. Tính độ dài đoạn thẳng MK . AC 1
Vì BC = 2AC nên cosACB = = hay ACB = 60 BC 2
Vì HO// AC (do cuøng vuoâng goùc vôùi AB) nên HOB = ACB = 60
Khi đó BM = O . B tan HOB = 4 3 2 MK IM  BM  3
Do MK // AC nên IKM ∽ ΔIAC  = = =   AC IC  BC  4
Mà AC = 4cm nên MK = 3cm .
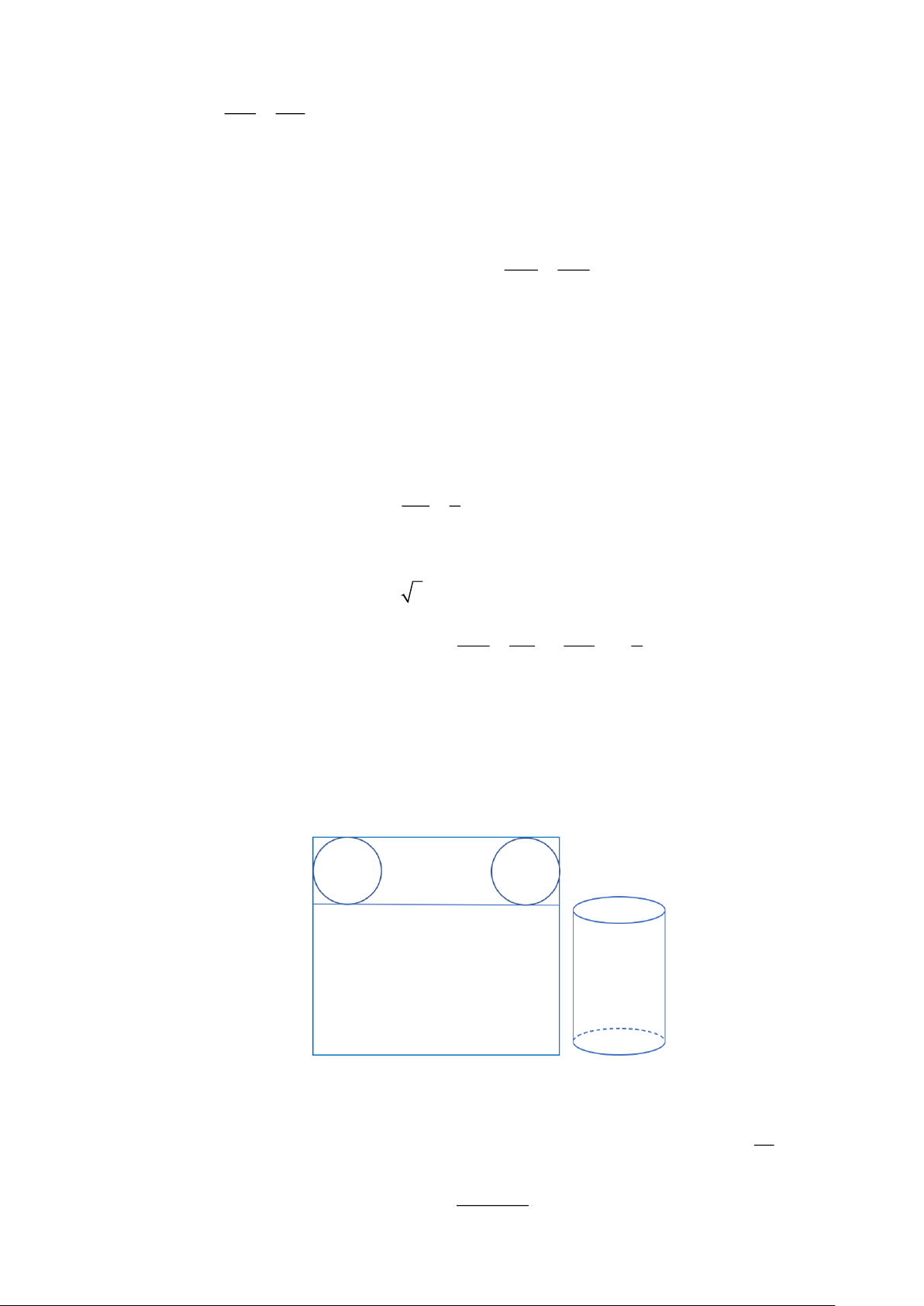
Câu 6. (0,5 điểm) Bạn Nam cắt một tấm bìa hình vuông cạnh 50 cm để được một hình chữ nhật và hai
hình tròn (như Hình 1). Bạn ấy cuộn tròn hình chữ nhật và dán hai mép giấy lại với nhau. Bạn ấy
dán tiếp hai hình tròn vào hai đầu để tạo thành một cái hộp hình trụ có nắp (như Hình 2).
Tính chiều cao của cái hộp tạo thành, biết chiều cao đó nhỏ hơn 50 cm , các mép dán không đáng kể. Hình 1 Hình 2 Lời giải 25
Gọi r là bán kính của đường tròn dây. Vì chu vi đáy bằng 2 r nên 2r = 50  r = ( cm ).  50( − ) 1
Chiều cao của cái hộp hình trụ là 50− 2r = ( cm ). 
---------------------------------@Hết@--------------------------------- Trang 4