Đề Thi Tuyển Sinh 10 Môn Toán Sở GD Lạng Sơn 2025-2026 Có Lời Giải

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT LẠNG SƠN Môn thi: Toán
Thời gian làm bài: 120 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
Đề thi gồm có 01 trang, 05 câu
Câu 1 (2,5 điểm)
a) Tính giá trị các biểu thức sau: + A = 16 − 4 B = ( − )2 4 15 + 15 12 27 C = 3  1 1  x + 4
b) Cho biểu thức P = + :  
, với x  0; x  9 .
 x − 3 x − 9  x + 3
1) Rút gọn biểu thức P . 1
2) Tìm giá trị của x để P = . 2
Câu 2 (1,0 điểm)
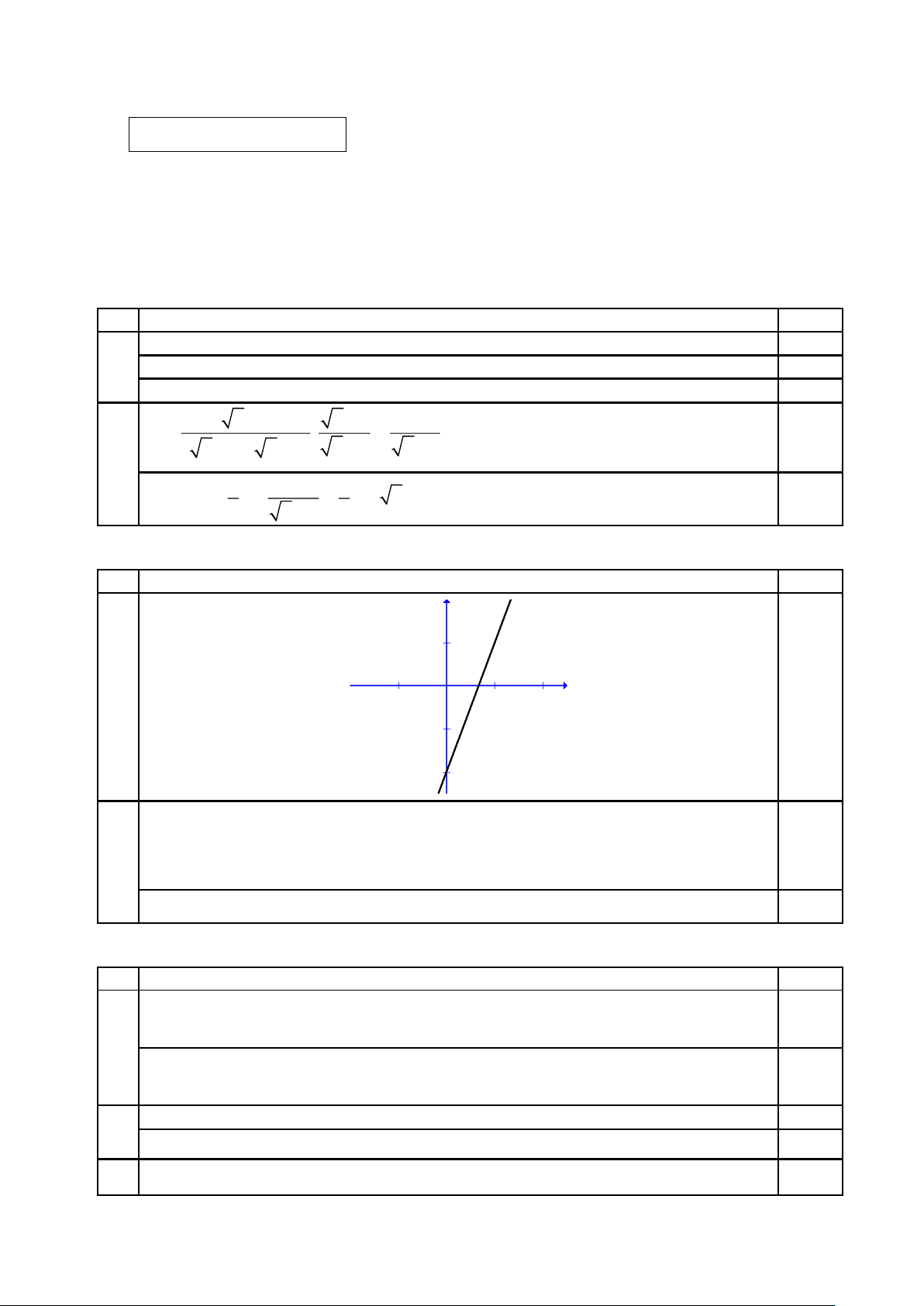
a) Vẽ đường thẳng (d ) : y = 3x − 2 .
b) Tìm tọa độ giao điểm của đồ thị hàm số (P) 2
: y = x với đường thẳng (d ) : y = 3x − 2 .
Câu 3 (2,5 điểm) x + y = 5
a) Giải hệ phương trình  . 3  x − 2y = 5 b) Giải phương trình 2
x − 9x +14 = 0. c) Cho phương trình 2
x − (m + 2) x + m − 3 = 0 (*) , với m là tham số.
1) Chứng minh rằng phương trình (*) luôn có hai nghiệm phân biệt với mọi m .
2) Tìm m để phương trình (*) có hai nghiệm x , x thỏa mãn x + x + 2x x  5 . 1 2 1 2 1 2
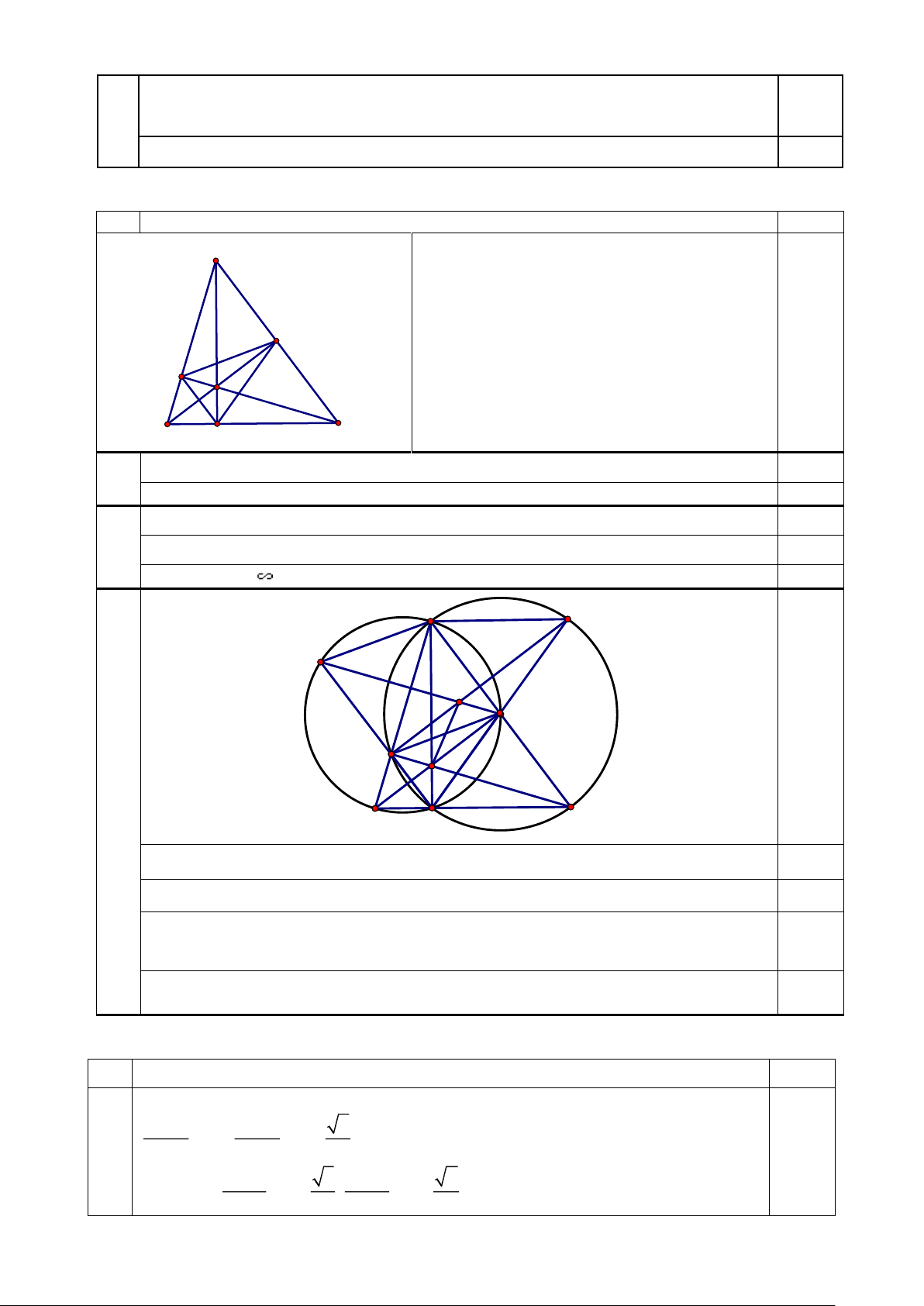
Câu 4 (3,5 điểm). Cho tam giác ABC không cân và có ba góc nhọn. Các đường cao AD, BE, CF
cắt nhau tại H (với D  BC, E C ; A F  AB ).
a) Chứng minh rằng tứ giác AFHE nội tiếp.
b) Chứng minh rằng EAD EFC.
c) Kẻ DE cắt đường tròn đường kính AC tại M ( M  D ); DF cắt đường tròn đường kính
AB tại N ( N  D ). Gọi K = FM  EN . Chứng minh rằng AF = AM và đường thẳng
EF đi qua trung điểm của đoạn thẳng HK .
Câu 5 (0,5 điểm). Cho các số thực dương a, b, c thỏa mãn a + b + c = 3 . Chứng minh rằng 3 3 3 a b c 3 + +  . 2 2 2
a + b b + c c + a 2
-----------------Hết-----------------
Họ và tên thí sinh:…………………………………….SBD:…………………………. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT LẠNG SƠN Môn thi: Toán
Hướng dẫn chấm gồm có 03 trang HƯỚNG DẪN CHẤM
Chú ý: - Học sinh có thể giải theo những cách khác nhau, nếu đúng thì giám khảo vẫn cho điểm tối
đa ứng với phần đó.
- Đối với bài hình học: Nếu học sinh không vẽ hình, hoặc vẽ hình sai không cho điểm.
- Điểm của bài thi không làm tròn, để lẻ đến 0,25 điểm. Câu 1 (2,5 điểm) Ý Nội dung Điểm A = 4 0,5 a B = 4 0,5 C = 5 0,5 x + 4 x + 3 1 P = ( = 0,5
x − 3)( x + 3). x + 4 x − 3 b 1 2 1 Ta có P = 
=  x − 3 = 2  x = 25 0,5 2 x − 2 2 Câu 2 (1,0 điểm) Ý Nội dung Điểm y 1 x 0,5 a -1 1 2 -1 -2
Phương trình hoành độ giao điểm của (P) và (d ) x =1 0,25 b 2
x = 3x − 2   x = 2
Tọa độ các giao điểm cần tìm là (1 ) ;1 , (2;4) . 0,25 Câu 3 (2,5 điểm) Ý Nội dung Điểm x + y = 5 x + y = 5    0,5 3  x − 2y = 5 5  y =10 a x = 3   . 0,5 y = 2 Ta có  = 25 0,25
b Phương trình có hai nghiệm phân biệt x = 7; x = 2 . 1 2 0,25
c 1) Ta có  = (m + )2 − (m − ) 2 2 4. 3 = m +16  0, . m 0,5 Trang 2
x + x = m + 2
2) Theo định lý Vi-ét ta có 1 2  . 0,25
x .x = m − 3  1 2
Do đó x + x + 2x x  5  3m − 4  5  m  3. 1 2 1 2 0,25 Câu 4 (3,5 điểm) Ý Nội dung Điểm A E
Vẽ hình đủ để giải ý a 0,5 F H B C D o o o
AEH + AFH = 90 + 90 = 180 0,75
Suy ra tứ giác AFHE nội tiếp. 0,25 EAH = EFH . 0,25
b Tứ giác DHEC nội tiếp, suy ra HDE = HCE 0,5 Suy ra EAD EFC. 0,25 A M N K E F H c B C D 5 điểm ,
A F, D,C, M cùng thuộc đường tròn, ADM = FCA. 0,25
Suy ra sđ AM = sđ AF  AM = AF . 0,25
AC ⊥ FM  FM // BE. Tương tự EN // CF 0,25 AC ⊥ BE 
Do đó, tứ giác FKEH là hình bình hành. Suy ra đường thẳng EF đi qua trung 0,25
điểm của đoạn thẳng HK . Câu 5 (0,5 điểm) Ý Nội dung Điểm
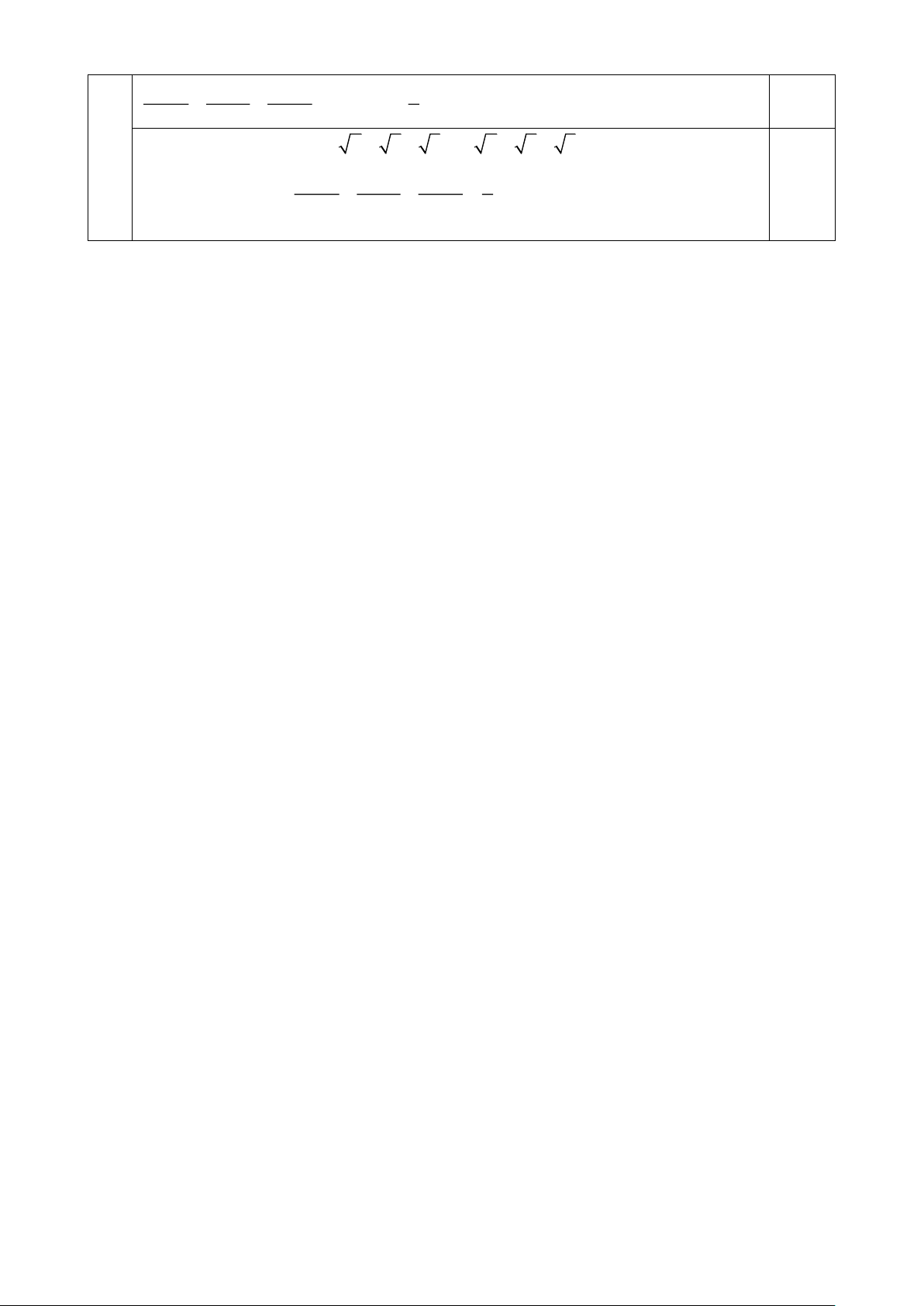
sử dụng bất đẳng thức Cô-si ta được 3 a ab b = a −  a − 2 2 a + b a + b 2 0,25 3 3 b c c a Tương tự,  b − ;  c − . 2 2 b + c 2 c + a 2 Trang 3 3 3 3 a b c 1 + +
 a + b + c −
a + b + c (1) 2 2 2 ( )
a + b b + c c + a 2
Có, a +1+ b +1+ c +1  2( a + b + c )  a + b + c  3 (2). 3 3 3 a b c 3 Từ (1) và (2) suy ra + +  . 0,25 2 2 2
a + b b + c c + a 2
Dấu bằng xảy ra khi vả chỉ khi a = b = c = 1. ---HẾT--- Trang 4