Đề Thi Tuyển Sinh 10 Môn Toán Sở GD Phú Yên 2025-2026 Có Lời Giải

SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 PHÚ YÊN Môn: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
I. Trắc nghiệm (3,0 điểm)
Câu 1: Biểu thức ( − )2 2 3 có giá trị là A. 3 − 2 . B. 2 − 3 . C. 7 − 4 3 . D. 1.
Câu 2: Tìm x thỏa mãn biểu thức 2 + x = 2 . A. x = 0 . B. x = 2 . C. x = 2 . D. x = 4 .
Câu 3: Hàm số nào sau đây là không phải là hàm số bậc nhất? x 2
A. y = 1− x . B. y = . C. y = . D. y = 2 (x − 2) . 2 x
Câu 4: Đường thẳng y = −x + 3 đi qua điểm M ( m;1) . Khi đó
A. m = 1 .B. m = 2 . C. m = 3 . D. m = 4 . ax − by = 2
Câu 5: Tìm các giá trị của a và b để hệ phương trình 
có nghiệm (1; −1) 2ax + by =1
A. a = 1;b = −1.
B. a = −1;b = 1.
C. a = 1;b = 1.
D. a = 2;b = 1 − .
Câu 6: Cho m , n là nghiệm của phương trình 2
x + mx + n = 0 , với m  0 ; n  0 . Thế thì tổng các nghiệm của phương trình bằng 1 − 1 A. 1 − . B. 1. C. . D. . 2 2 A N T F E 6 m I 3 m M G P S K B H R Hình 1 Hình 2 Hình 3
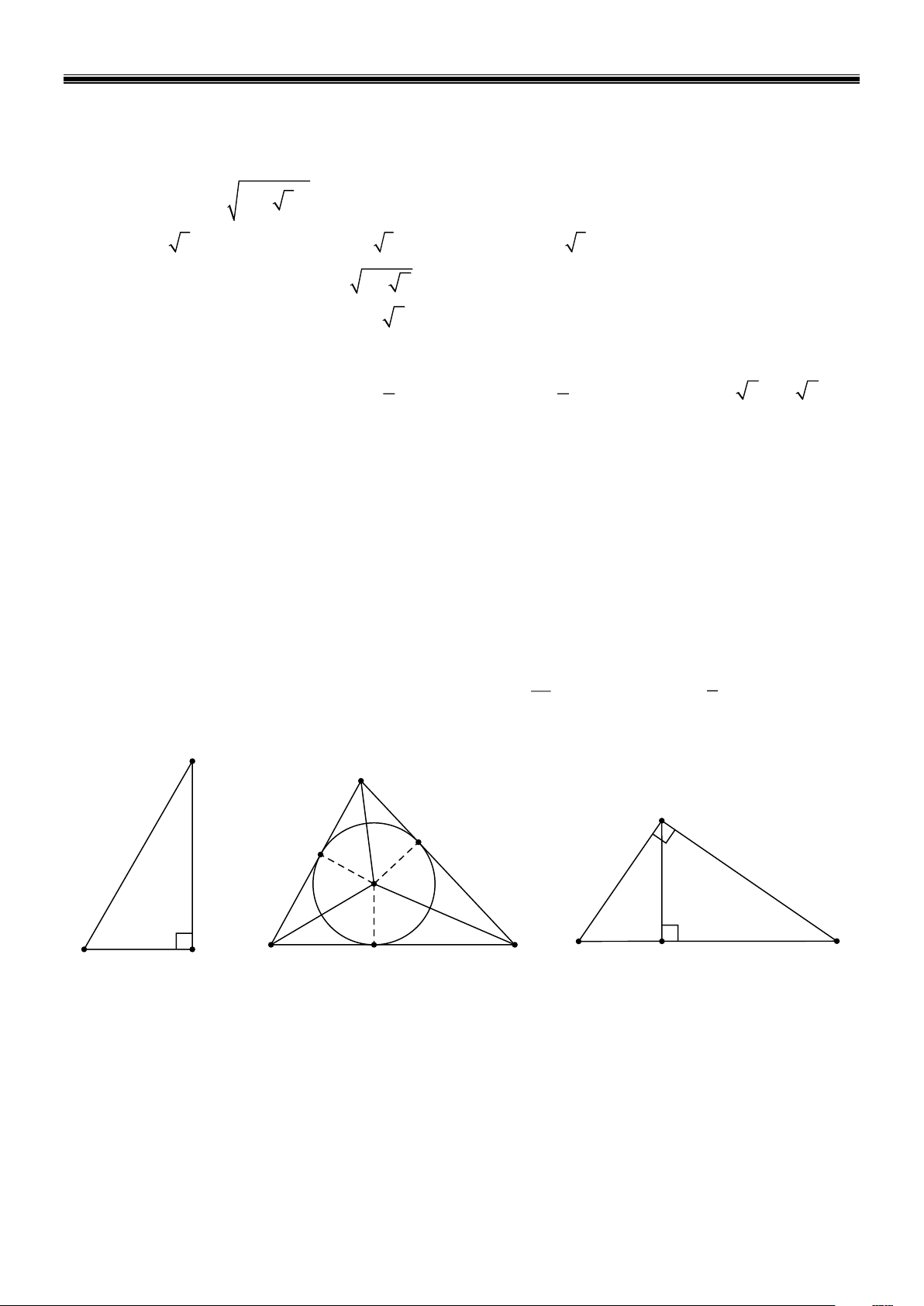
Câu 7: Một cái thang AB dài 6m tựa vào tường, chân thang cách tường 3m ( Hình 1). Tính góc tạo
bởi thang AB và tường AH . A. 30 . B. 45 . C. 60 . D. 90 .
Câu 8: Tam giác nhọn MNP có đường tròn (I ) nội tiếp, với E , F ,G là các tiếp điểm ( Hình 2).
Khẳng định nào sau đây không đúng?
A. IGP = 90 .
B. ME = MG .
C. MNI = INP .
D. N ; I ;G thẳng hàng.
Câu 9: Cho tam giác STR vuông tại T , đường cao TK ( Hình 3). Khẳng định nào sau đây sai? Trang 1 1 1 1 A. = + . B. 2 2 2
SR = ST + TR . C. 2
ST = SK.SR .
D. TS.TR = TK.SR . TK TS TR M D E B R H K N P Q J O A K C G I F S Hình 4 Hình 5 Hình 6
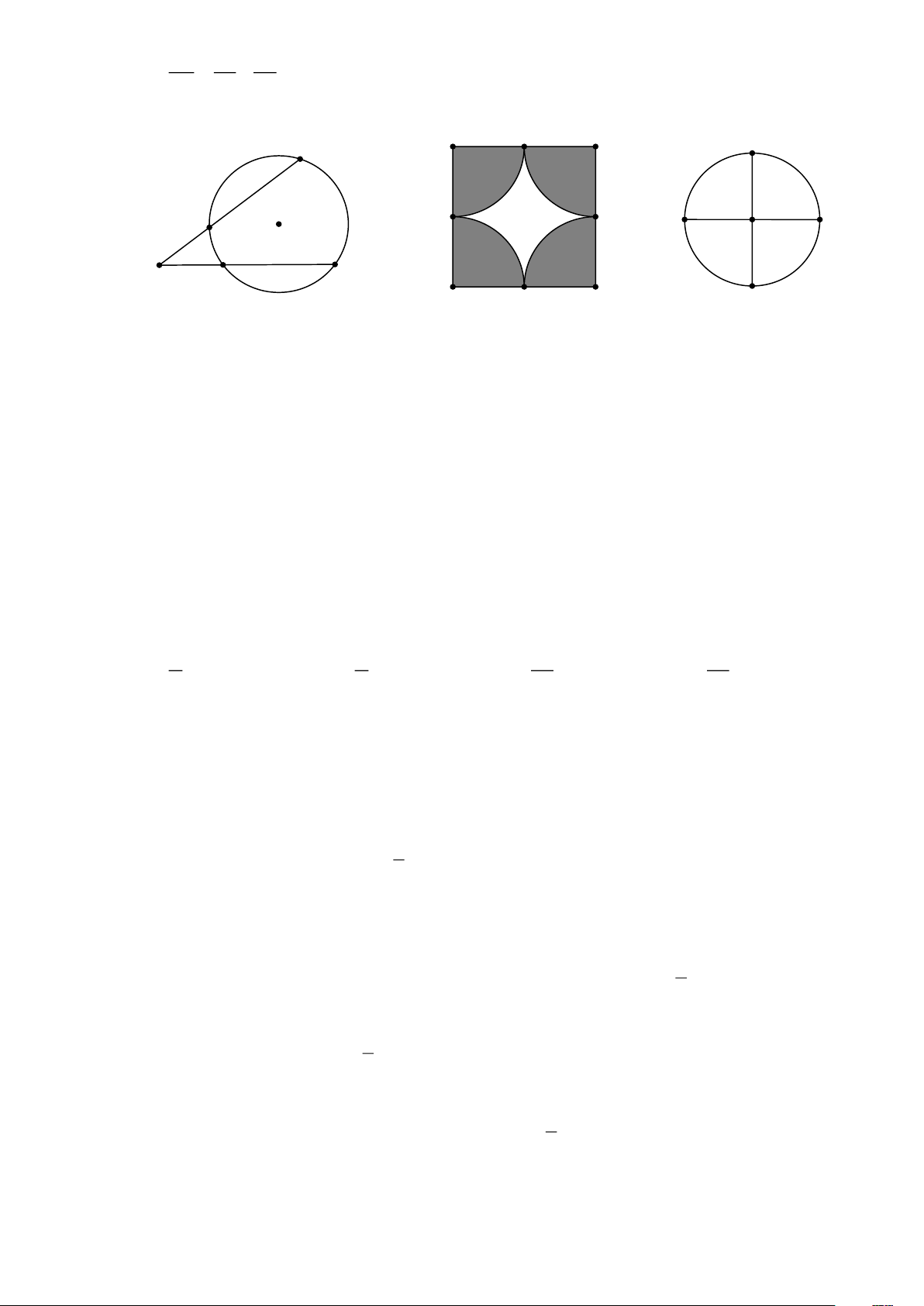
Câu 10: Từ một điểm A nằm ngoài đường tròn ( J ) , kẻ hai cát tuyến AHB và AKC ( Hình 4). Biết
BAC = 40 ; các cung HB, BC, CK có cùng độ dài. Tìm số đo HCK . A. 30 . B. 20 . C. 15 . D. 10 .
Câu 11: Hình vuông DEFG có cạnh bằng 2cm ; M ; N; I; K là trung điểm các cạnh (Hình 5). Tính diện
tích phần màu trắng giới hạn bởi 4 cung tròn KM ; MN ; NI ; IK (tâm là các đỉnh hình vuông). A. 2 4 − (cm ) . B. 2  − 4(cm ) . C. 2  (cm ) . D. 2 4(cm ) .
Câu 12: Đường tròn (O) có bán kính bằng1cm . Hai đường kính PQ và RS vuông góc với nhau (Hình
6). Tính độ dài cung lớn PR .   3 3 A. (cm) . B. (cm) . C. (cm) . D. (cm) . 4 2 4 2
II. Tự luận (7,0 điểm)
Câu 13. (1,5 điểm) Giải các phương trình, hệ phương trình sau: a) 2 2x + 5x + 2 = 0 xy = 3 − b)  3
 x + 3y + 2xy = 0 1
Câu 14. (2,0 điểm) Cho hai hàm số 2
y = − x và y = ax + b . 2
a) Tìm các hệ số a,b biết đường thẳng y = ax + b đi qua điểm M ( 2 − ; 2 − ), N (4 ) ;1 .
b) Với các giá trị a,b vừa tìm được, hãy: 1
+ Tìm giao điểm của đường thẳng y = ax + b và đồ thị hàm số 2
y = − x bằng phương pháp 2 đại số. 1
+ Vẽ đồ thị hai hàm số 2
y = − x và y = ax + b trên cùng một mặt phẳng tọa độ. 2
Câu 15. (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình 2
Một khu đất hình chữ nhật có tỷ số hai kích thước là . Người ta làm một sân bóng đá mini 5 3
người ở giữa, chừa lối đi xung quanh (lối đi thuộc khu đất). Lối đi rộng 2 m và có diện tích 2
224 m . Tính các kích thước của khu đất. Câu 16. (2,0 điểm) Trang 2
Cho tam giác ABC vuông tại A , có AB = 3 cm, AC = 4 cm . Đường tròn tâm B bán kính BA
và đường tròn tâm C bán kính CA cắt nhau tại điểm thứ hai D .
a) Chứng minh rằng tứ giác ABDC là tứ giác nội tiếp.
b) Tính độ dài đoạn AD .
c) Một đường thẳng d quay quanh A cắt (B) tại E (E  A) và cắt (C) tại F (F  A) . Gọi
M là giao điểm của EB và FC . Khi d thay đổi thì điểm M chạy trên đường nào?
-------------------------------@Hết@----------------------------------- HƯỚNG DẪN GIẢI
I. Trắc nghiệm (3,0 điểm)
Câu 1: Biểu thức ( − )2 2 3 có giá trị là A. 3 − 2 . B. 2 − 3 . C. 7 − 4 3 . D. 1. Lời giải ( − )2 2 3 = 2 − 3 = 2 − 3
Câu 2: Tìm x thỏa mãn biểu thức 2 + x = 2 . A. x = 0 . B. x = 2 . C. x = 2 . D. x = 4 . Lời giải
2 + x = 2 (1) ĐKXĐ: x  0
(1)  2 + x = 4  x = 2  x = 4 ( TMĐK)
Câu 3: Hàm số nào sau đây là không phải là hàm số bậc nhất? x 2
A. y = 1− x . B. y = . C. y = . D. y = 2 (x − 2) . 2 x Lời giải 2
Hàm số y = không có dạng y = ax + b nên không là hàm số bậc nhất. x
Câu 4: Đường thẳng y = −x + 3 đi qua điểm M ( m;1) . Khi đó
A. m = 1 B. m = 2 . C. m = 3 . D. m = 4 . Lời giải
Đường thẳng y = −x + 3 đi qua điểm M ( m;1) nên 1 = −m + 3  m = 2 ax − by = 2
Câu 5: Tìm các giá trị của a và b để hệ phương trình 
có nghiệm (1; −1) 2ax + by =1
A. a = 1;b = −1.
B. a = −1;b = 1.
C. a = 1;b = 1.
D. a = 2;b = −1. . Lời giải ax − by = 2 Hệ phương trình  có nghiệm (1; −1) 2ax + by =1  . a 1− . b ( 1 − ) = 2 a + b = 2 3  a = 3 a =1         2 . a 1+ b( 1 − ) =1 2a − b =1 b  = 2a −1 b  =1 Trang 3
Câu 6: Cho m , n là nghiệm của phương trình 2
x + mx + n = 0 , với m  0 ; n  0 . Thế thì tổng các nghiệm của phương trình bằng 1 − 1 A. 1 − . B. 1. C. . D. . 2 2 Lời giải
m , n là nghiệm của phương trình 2
x + mx + n = 0 nên theo định lý Vi et có m + n = m − .
m n = n  m = 1 ( Vì n  0 )
Khi đó m + n = −1
Vậy tổng hai nghiệm bằng 1 − . A N T F E 6 m I 3 m M G P S K B H R Hình 1 Hình 2 Hình 3
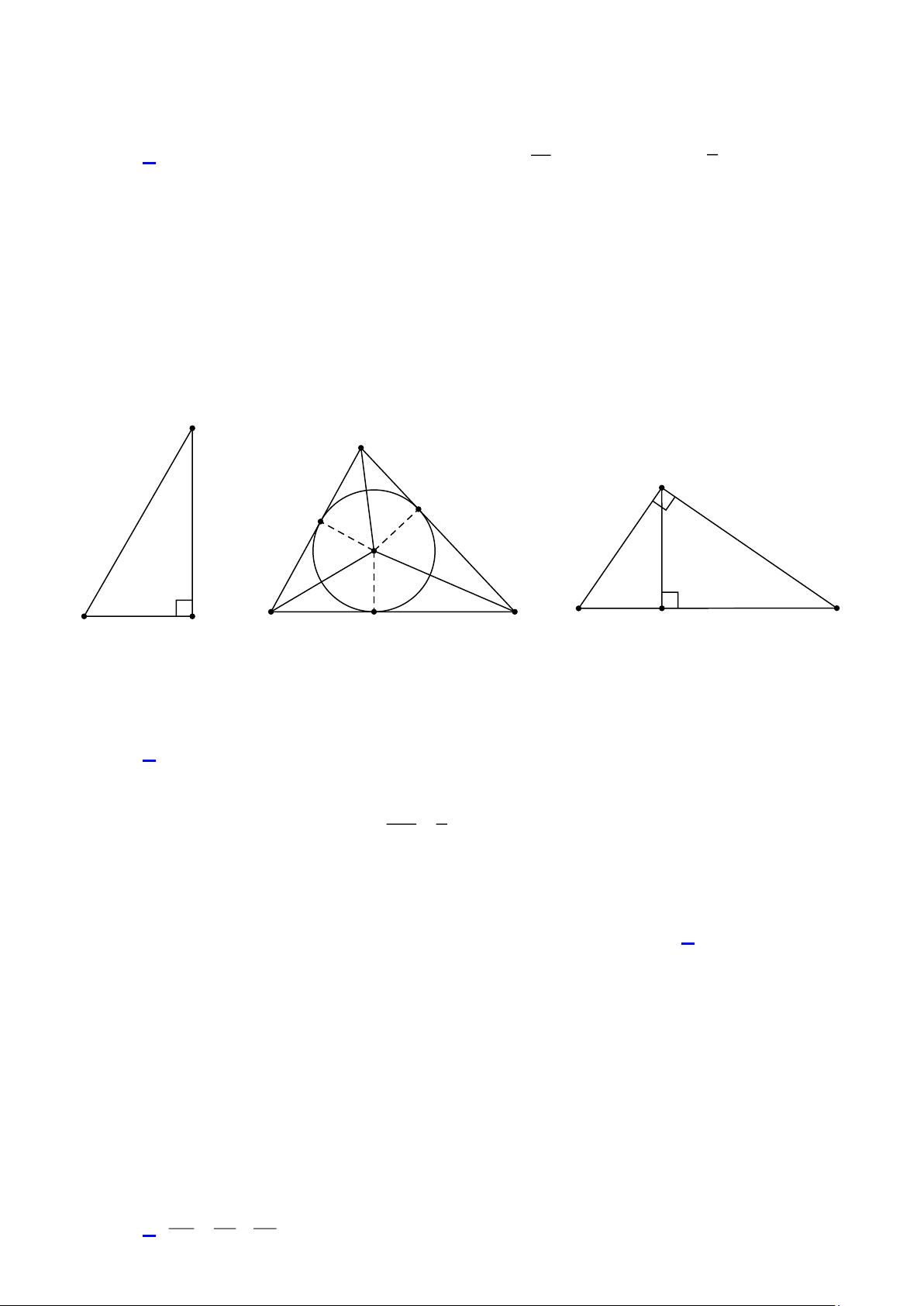
Câu 7: Một cái thang AB dài 6m tựa vào tường, chân thang cách tường 3m ( Hình 1). Tính góc tạo
bởi thang AB và tường AH . A. 30 . B. 45 . C. 60 . D. 90 . Lời giải  BH 1
ABH vuông tại H có sin A A 30 = =  = . AB 2
Câu 8: Tam giác nhọn MNP có đường tròn (I ) nội tiếp, với E , F ,G là các tiếp điểm ( Hình 2).
Khẳng định nào sau đây không đúng?
A. IGP = 90 .
B. ME = MG .
C. MNI = INP .
D. N ; I ;G thẳng hàng. Lời giải
Tam giác nhọn MNP có đường tròn (I ) nội tiếp, với E , F ,G là các tiếp điểm nên :
IG ⊥ MP = IGP = 90
ME = MG ( tính chất hai tiếp tuyến cắt nhau).
MNI = INP ( vì tâm I là giao điểm 3 đường phân giác). Đáp án D sai.
Câu 9: Cho tam giác STR vuông tại T , đường cao TK ( Hình 3). Khẳng định nào sau đây sai? 1 1 1 A. = + . B. 2 2 2
SR = ST + TR . C. 2
ST = SK.SR .
D. TS.TR = TK.SR . TK TS TR Trang 4 Lời giải
Tam giác STR vuông tại T , đường cao TK nên ta có: 2 2 2
SR = ST + TR ( định lý Pytago) 2
ST = SK.SR ; TS.TR = TK.SR ( hệ thức giữa cạnh và đường cao trong tam giác vuông) Khẳng định A sai. M D E B R H K N P Q J O A K C G I F S Hình 4 Hình 5 Hình 6
Câu 10: Từ một điểm A nằm ngoài đường tròn ( J ) , kẻ hai cát tuyến AHB và AKC ( Hình 4). Biết
BAC = 40 ; các cung HB, BC, CK có cùng độ dài. Tìm số đo HCK . A. 30 . B. 20 . C. 15 . D. 10 . Lời giải 1
Xét đường tròn ( J ) có BAC = (sđ C
B − sđ HK ) = 40 ( góc có đỉnh nằm ngoài đường tròn) 2
 sđ BC − sđ HK = 80 (1)
Mặt khác sđ HB + sđ BC + sđCK + sđ HK = 360
Mà các cung HB, BC, CK có cùng độ dài  sđ HB = sđ BC = sđCK
Do đó 3.sđ BC + sđ HK = 360 (2)
Từ (1) và (2) suy ra  4.sđ BC = 360 + 80 = 440  sđ BC = 0 11 
 sđ HK = 110 − 80 = 30 1 1
HCK = sđ HK = .30 = 15 . 2 2
Câu 11: Hình vuông DEFG có cạnh bằng 2cm; M ; N; I; K là trung điểm các cạnh (Hình 5). Tính diện
tích phần màu trắng giới hạn bởi 4 cung tròn KM ; MN ; NI ; IK (tâm là các đỉnh hình vuông). A. 2 4 − (cm ) . B. 2  − 4(cm ) . C. 2  (cm ) . D. 2 4(cm ) . Lời giải
Diện tích hình vuông DEFG là: 2 2.2 = 4(cm )
Diện tích 4 cung tròn tại 4 góc hình vuông (tâm là các đỉnh hình vuông) bằng diện tích hình
tròn bán kính 1cm và bằng: 2 2 .1 =  (cm )
Vậy diện tích phần màu trắng giới hạn bởi 4 cung tròn KM ; MN ; NI ; IK là 2 4 − (cm )
Câu 12: Đường tròn (O) có bán kính bằng1cm . Hai đường kính PQ và RS vuông góc với nhau (Hình
6). Tính độ dài cung lớn PR .   3 3 A. (cm) . B. (cm) . C. (cm) . D. (cm) . 4 2 4 2 Trang 5 Lời giải
Hai đường kính PQ và RS vuông góc với nhau nên POR = 90 .1.90 
Độ dài cung nhỏ PR là l = = (cm) PR 180 2  3
Độ dài cung lớn PR là : 2.1− = (cm) . 2 2
II. Tự luận (7.0 điểm)
Câu 13. (1,5 điểm) Giải các phương trình, hệ phương trình sau: a) 2 2x + 5x + 2 = 0 xy = 3 − b)  3
 x + 3y + 2xy = 0 Lời giải a) 2 2x + 5x + 2 = 0 Ta có: 2
Δ = 5 − 4.2  2 = 9  0 5 − + 9 1 5 − − 9
Suy ra phương trình có 2 nghiệm phân biệt là: x = = − ; x = = 2 − 1 2 2.2 2 2.2  1 
Vậy tập nghiệm của phương trình là: S = − ; 2 −   2  xy = 3 − xy = 3 − xy = 3 − b)     
3x + 3y + 2xy = 0
3x + 3y − 6 = 0   x + y = 2
Suy ra x, y là nghiệm của phương trình 2
t − 2t − 3 = 0
Vì a − b + c = 1− ( 2)
− − 3 = 0 nên phương trình có hai nghiệm phân biệt là: t = 1; − t = 3 1 2
Vậy hệ phương trình có 2 nghiệm là: ( ; x y) = (3;− ) 1 ; ( ; x y) = ( 1 − ;3) . 1
Câu 14. (2,0 điểm) Cho hai hàm số 2
y = − x và y = ax + b . 2
a) Tìm các hệ số a,b biết đường thẳng y = ax + b đi qua điểm M ( 2 − ; 2 − ), N (4 ) ;1 .
b) Với các giá trị a,b vừa tìm được, hãy: 1
+ Tìm giao điểm của đường thẳng y = ax + b và đồ thị hàm số 2
y = − x bằng phương pháp 2 đại số. 1
+ Vẽ đồ thị hai hàm số 2
y = − x và y = ax + b trên cùng một mặt phẳng tọa độ. 2 Lời giải
a) Tìm các hệ số a,b biết đường thẳng y = ax + b đi qua điểm M ( 2 − ; 2 − ), N (4 ) ;1 .
Do đường thẳng y = ax + b đi qua điểm M ( 2 − ; 2
− ) nên thay x = −2, y = −2 vào y = ax + b ta được phương trình 2 − = 2
− a + b  −2a + b = −2 (1)
Do đường thẳng y = ax + b đi qua điểm N (4; )
1 nên thay x = 4, y = 1 vào y = ax + b ta được phương
trình 1 = 4a + b  4a + b = 1( 2)
Từ (1) và (2) ta có hệ phương trình: Trang 6    1  2 − a + b = 2 − 6a = 3 a =      2 4a + b = 1 b = 1− 4a   b     = 1 −  1 a = Vậy  2 b = −1
b) Với các giá trị a,b vừa tìm được, hãy: 1
+ Tìm giao điểm của đường thẳng y = ax + b và đồ thị hàm số 2
y = − x bằng phương pháp đại số. 2  1 a = 1 Với 
2 thì phương trình đường thẳng có dạng y = x −1  2 b = −1 1 1
Xét phương trình hoành độ giao điểm của y = x −1 và 2
y = − x ta có 2 2 1 2 1 − x = x −1 2 2 2
 −x = x − 2 2
 x + x − 2 = 0
 (x + 2)(x − ) 1 = 0 x = 2 −    x =1 1
Với x = −2 thay vào y = x −1 ta được y = −2 2 1 1
Với x = 1 thay vào y = x −1 ta được y = − 2 2 1 1  
Vậy giao điểm của đồ thị hàm số y = x −1 và 2
y = − x là (− − ) 1 2, 2 ; 1 − , −   2 2  2  1
+ Vẽ đồ thị hai hàm số 2
y = − x và y = ax + b trên cùng một mặt phẳng tọa độ. 2 1
* Vẽ đồ thị hàm số y = x −1 2 1  
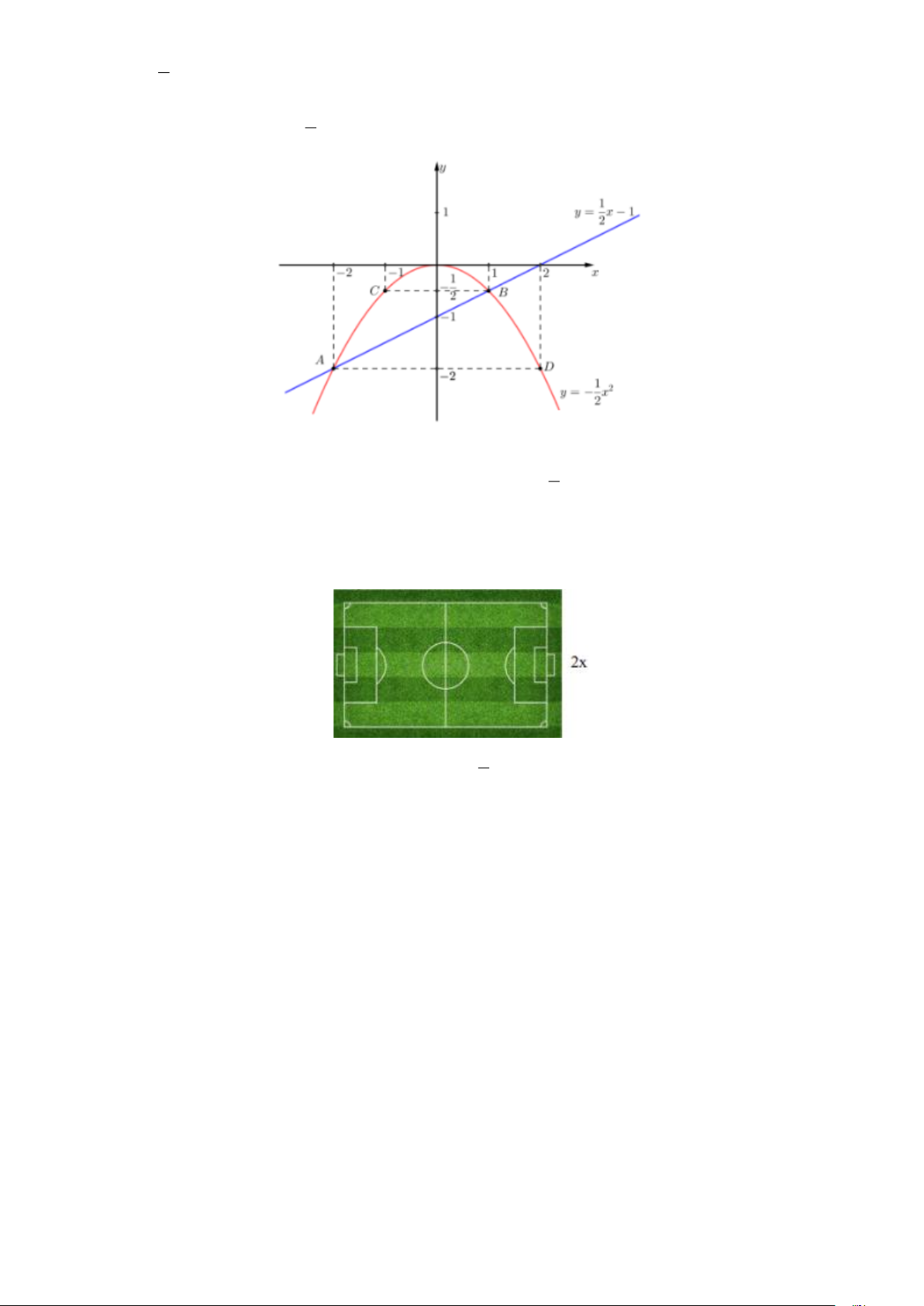
Đồ thị hàm số y = x −1 là đường thẳng đi qua hai điểm A(− − ) 1 2, 2 ; B 1 − ,−   2  2  1 * Vẽ đồ thị hàm số 2 y = − x 2 Ta có bảng giá trị sau: x -2 -1 0 1 2 1 1 1 2 y = − x -2 − 0 − -2 2 2 2
 Đồ thị hàm số là đường cong parabol đi qua các điểm ( )     A(− − ) 1 1 0;0 ; 2; 2 ; B 1;− ;C 1 − ;− ; D(2; 2 −     )  2   2  Trang 7 1
Hệ số a = −  0 nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng. 2 1
Ta vẽ được đồ thị hàm số 2
y = − x như sau: 2
Câu 15. (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình 2
Một khu đất hình chữ nhật có tỷ số hai kích thước là . Người ta làm một sân bóng đá mini 5 3
người ở giữa, chừa lối đi xung quanh (lối đi thuộc khu đất). Lối đi rộng 2 m và có diện tích 2
224 m . Tính các kích thước của khu đất. Lời giải 2
Vì mảnh đất là hình chữ nhật có tỉ số hai kích thước là . 3
Gọi 2x( m) là chiều rộng của mảnh đất (x  0)
3x( m) là chiều dài của mảnh đất.
Khi đó diện tích cả mảnh đất là: 2
x  x = x ( 2 2 3 6 m ) .
Phần sân bóng có chiều rộng là: 2x − 4(m)
Phần sân bóng có chiều dài là: 3x − 4(m)
Diện tích phần sân bóng là:
( x − )( x − ) 2 2
= x − x − x + = x − x + ( 2 2 4 3 4 6 8 12 16 6 20 16 m ).
Khi đó diện tích lối đi là: 2 x − ( 2 x − x + ) 2 2
= x − x + x − = x − ( 2 6 6 20 16 6 6 20 16 20 16 m ).
Theo đề ra ta có diện tích lối đi bằng 2 224 m nên
20x −16 = 224  20x = 240  x = 12(m).
Vậy khu đất có chiều dài là 36 m , chiều rộng là 24 m . Câu 16. (2,0 điểm) Trang 8
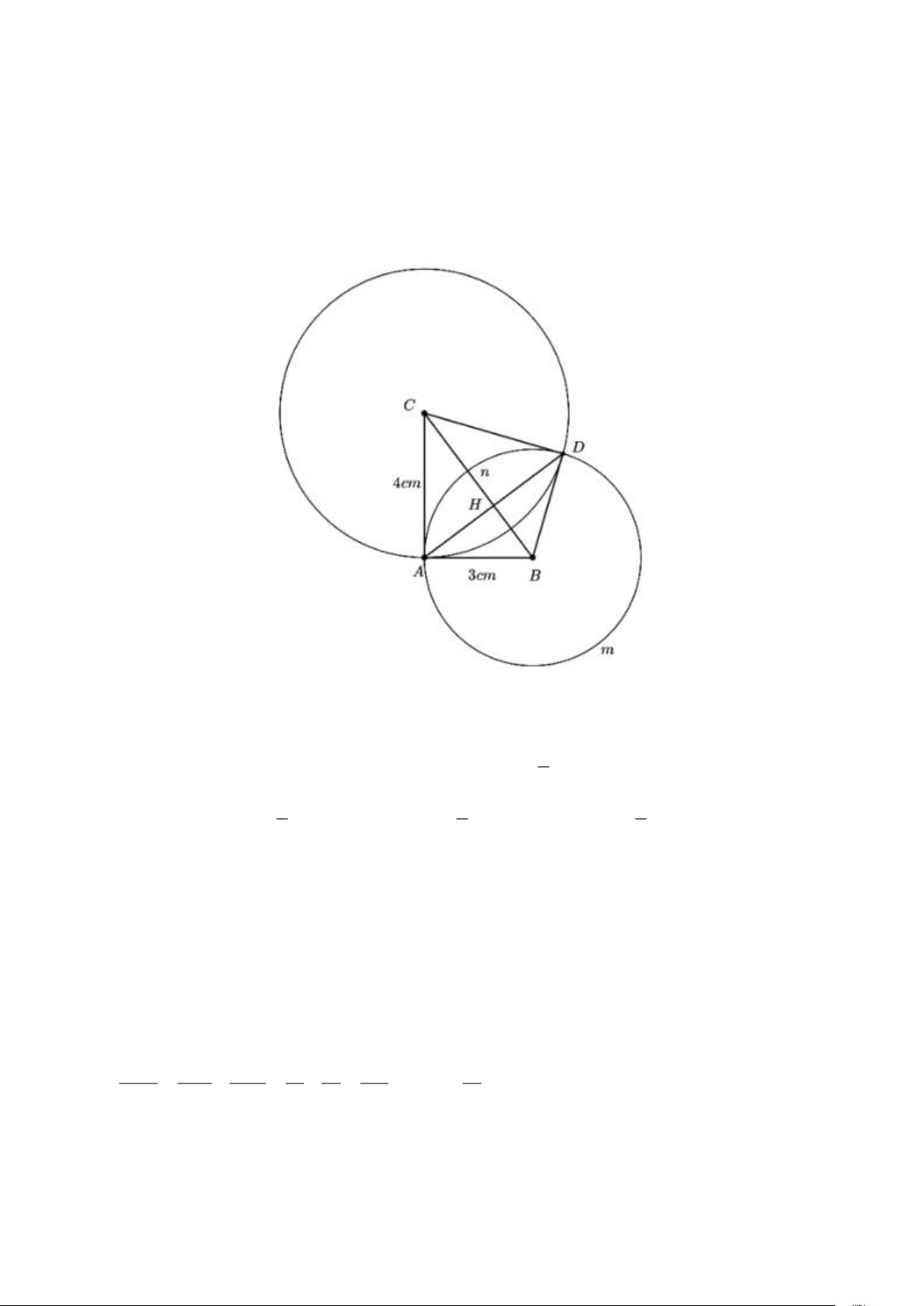
Cho tam giác ABC vuông tại A , có AB = 3 cm, AC = 4 cm . Đường tròn tâm B bán kính BA
và đường tròn tâm C bán kính CA cắt nhau tại điểm thứ hai D .
a) Chứng minh rằng tứ giác ABDC là tứ giác nội tiếp.
b) Tính độ dài đoạn AD .
c) Một đường thẳng d quay quanh A cắt (B) tại E (E  A) và cắt (C) tại F (F  A) . Gọi
M là giao điểm của EB và FC . Khi d thay đổi thì điểm M chạy trên đường nào? Lời giải
a) Chứng minh tứ giác ABDC nội tiếp được.
Xét đường tròn tâm B có ABD = sđ AnD ACD 1
là góc có đỉnh bên ngoài đường tròn tâm B nên ACD = (sđ AmD − sđ AnD) 2 1  1 1
ABD + ACD = sđ AnD + (sđ AmD − sđ AnD) = (sđ AmD + sđ AnD) = 360 =180 2 2 2
 ABDC là tứ giác có tổng 2 góc đối bằng 180
 ABDC là tứ giác nội tiếp
b) Tính độ dài đoạn AD .
Ta có BA = BD (= 3 cm) và CA = CD(= 4 cm)
 BC là trung trực của AD  BC ⊥ AD
Gọi H là giao điểm của AD và BC
Xét ABC vuông tại A , đường cao AH 1 1 1 1 1 25 12  = + = + =  AH = (cm) 2 2 2 2 2 AH AB AC 3 4 144 5
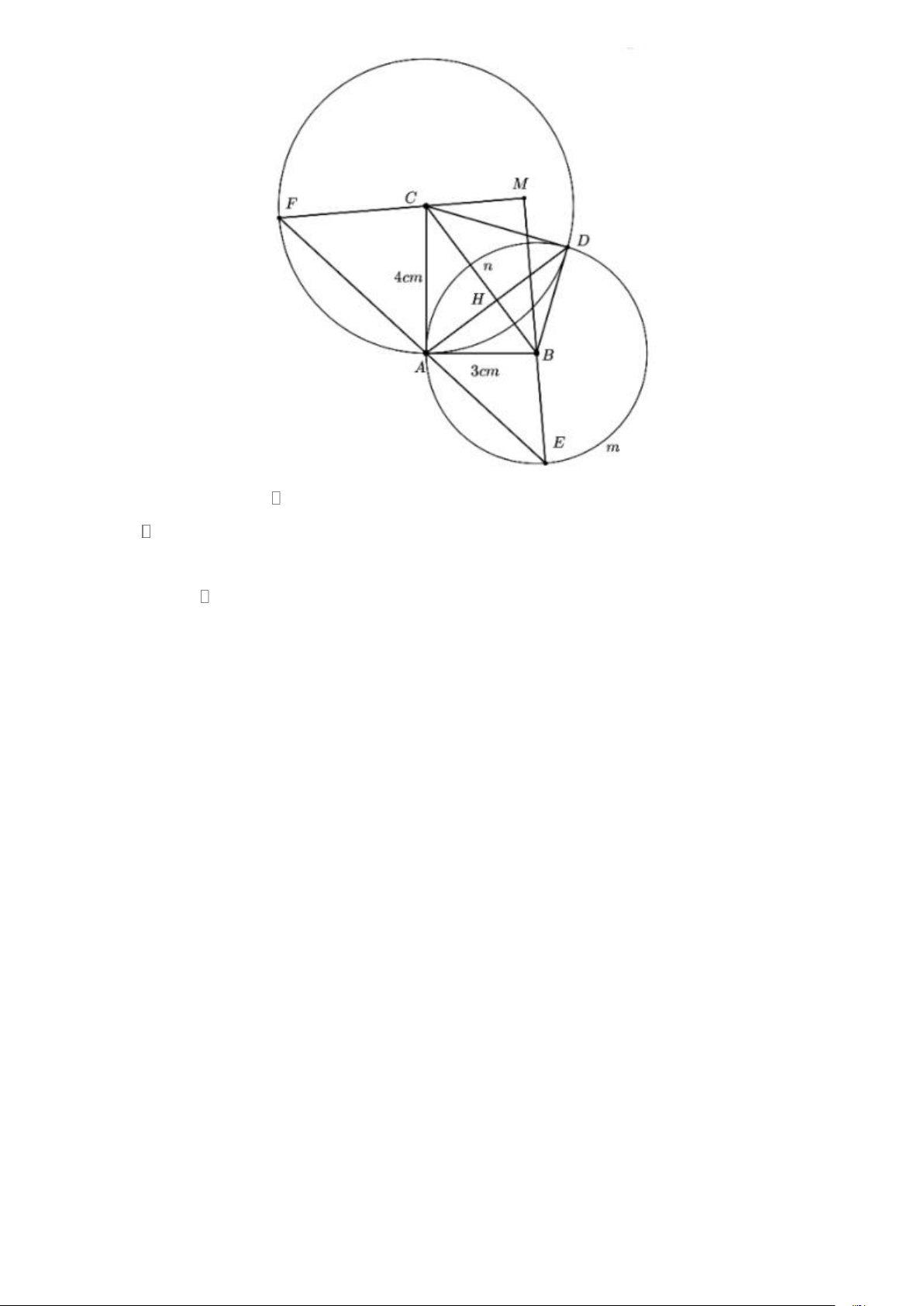
c) Một durờng thẳng d quay quanh A cắt (B) tại E (E  A) và cắt (C) tại F (F  A) . Gọi M là giao
điểm của EB và FC . Khi d thay đổi thì điểm M chạy trên đường nào? Trang 9
Ta có CF = CA = 4cm nên CAF cân tại C  F = CAF (tính chất)
Tương tự BAE cân tại B nên E = BAE (tính chất)
Mà CAF + BAE = 180 − CAB = 180 − 90 = 90
 E + F = 90  MEF vuông tại M (tổng các góc trong một tam giác)
Xét tứ giác MCAB có CMB + CAB = 90 + 90 = 180
Mà 2 góc này ở vị trí đối diện nên MCAB nội tiếp có đường kính BC
Mà BC cố định nên M luôn thuộc đường tròn đường kính BC cố định. Trang 10