Đề Thi Tuyển Sinh 10 Môn Toán Sở GD Thái Bình 2025-2026 Có Lời Giải

SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THÁI BÌNH Môn: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Câu 1. (2,0 điểm)  x − 6 x +1 x −1 x + 4 x
Cho hai biểu thức P =  −  :  và Q =
(với x  0; x  1). x 1 x +1 − 1− x   x + 4
a) Tính giá trị biểu thức Q với x = 4 .
b) Chứng minh rằng P = 4Q .
c) Tìm tất cả các giá trị của x để P nhận giá trị là số nguyên. Câu 2. (2,0 điểm) mx + y = 3 Cho hệ phương trình 
(với m là tham số). −x + y = 2
a) Giải hệ phương trình với m = 2 .
b) Tìm m để hệ phương trình có nghiệm duy nhất ( x; y) thỏa mãn 2 2 x + y = 10 . Câu 3.
(2,0 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol (P) 2
: y = 2x và đường thẳng
(d ): y = x + m (với m là tham số).
a) Tìm m để (d ) đi qua điểm A(2;8) .
b) Tìm m để (d ) cắt (P) tại hai điểm phân biệt có hoành độ x , x thỏa mãn: 1 2
x + x − 3x x = 5. 1 2 1 2 Câu 4. (3,5 điểm)
b) Cho tam giác ABC nhọn, nội tiếp đường tròn (O; R) . Kẻ AH vuông góc với BC tại H ,
HK vuông góc với AB tại K và HI vuông góc với AC tại I .
a) Chứng minh tứ giác AKHI nội tiếp đường tròn.
b) Gọi E là giao điểm của AH với KI . Chứng minh rằng .
EA EH = EK.EI .
c) Chứng minh KI vuông góc với AO .
d) Giả sử điểm A và đường tròn (O; R) cố định, còn dây BC thay đổi sao cho 2 . AB AC = 3R .
Xác định vị trí của dây cung BC sao cho tam giác ABC có diện tích lớn nhất.
2) Một hình nón có diện tích đáy bằng ( 2
16 cm ) và có chiều cao gấp ba lần bán kính đáy.
Tính thể tích của hình nón đó. Câu 5. (0,5 điểm)
Cho các số thực dương x, y, z thỏa mãn x + y + z = 6. Tìm giá trị lớn nhất của biểu thức 3 3 3 xy yz zx P = + + . 3 3 3
y + 4 z + 4 x + 4
---------------------------------@Hết@--------------------------------- Trang 1 HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm)  x − 6 x +1 x −1 x + 4 x
Cho hai biểu thức P =  −  :  và Q =
(với x  0; x  1). x 1 x +1 − 1− x   x + 4
a) Tính giá trị biểu thức Q với x = 4 .
b) Chứng minh rằng P = 4Q .
c) Tìm tất cả các giá trị của x để P nhận giá trị là số nguyên. Lời giải x
a) Theo bài ra Q =
với x  0; x  1 x + 4 4 2 1
Thay x = 4 (thỏa mãn điều kiện) vào biểu thức Q ta có: Q = = = . 4 + 4 8 4
b) Với x  0; x  1 ta có:  x − 6 x +1 x −1 x + 4 P =  −  :  x 1 x +1 − 1− x     x − 6 x +1 x −1 x + 4 P =  ( −  x − ) 1 ( x +  ) : 1 x +1 1− x  x −
x + − ( x − )2 6 1 1 1− x p = ( x − ) 1 ( x + ) . 1 x + 4
x − 6 x +1− x + 2 x −1 1− x P = . x −1 x + 4 4 − x −( x − ) 1 P = . x −1 x + 4 4 x P = x + 4 x P = 4. = 4.Q x + 4
Vậy P = 4Q với x  0; x  1. 4 x c) Ta có P =
với x  0; x  1. x + 4 4 x
Với x  0; x  1 ta có 4 x  0; x + 4  0  P =  0 ( ) 1 x + 4
x + − (x − x + ) ( x − )2 4 4 4 2 Ta cũng có: P = = 1−
 1 với x  0; x  1 x + 4 x + 4 4 x Do đó P = 1 (2) x + 4 Từ ( )
1 và (2)  0  P  1. Mà P nhận giá trị là số nguyên nên P 0  ;1 . x + Với P = 4 0 
= 0  x = 0  x = 0 (thỏa mãn) x + 4 Trang 2 x + Với P = 1  =  x + = x  x + −
x =  ( x − )2 4 1 4 4 4 4 0 2 = 0 x + 4
 x − 2 = 0  x = 4 (thỏa mãn). Vậy x 0; 
4 thì P nhận giá trị là số nguyên. Câu 2. (2,0 điểm) mx + y = 3 Cho hệ phương trình 
(với m là tham số). −x + y = 2
a) Giải hệ phương trình với m = 2 .
b) Tìm m để hệ phương trình có nghiệm duy nhất ( x; y) thỏa mãn 2 2 x + y = 10 . Lời giải
a) Với m = 2 hệ phương trình đã cho trở thành:  1  1 x = x = 2x + y = 3 3  x =1     3 3        −x + y = 2 −x + y = 2 1 7  y 2  − + = y =  3  3  
Vậy với m = 2 hệ phương trình đã cho có nghiệm duy nhất ( x y) 1 7 ; = ;   .  3 3  mx + y = 3  ( )1
b) Xét hệ phương trình  −x + y = 2  (2)
Từ (2) ta có y = x + 2 (3) . Thay (3) vào ( )
1 ta được: mx + x + 2 = 3  (m + ) 1 x = 1 (4)
Hệ phương trình có nghiệm duy nhất khi phương trình (4) có nghiệm duy nhất
 m +1  0  m  −1 1
Với m  −1 phương trình (4) có 1 nghiệm x = . m +1 1 2m + 3 Từ (2) ta có y = + 2 = . m +1 m +1  1 x =  +
Với m  −1, hệ phương trình có nghiệm duy nhất m 1  2m + 3 y =  m +1 2 2  1   2m + 3  Theo bài ra 2 2 x + y = 10  + =10      m +1  m +1 
 + ( m + )2 = (m + )2 1 2 3 10 1 2 2
 1+ 4m +12m + 9 = 10m + 20m +10 2  6m + 8m = 0
 2m(3m + 4) = 0 m = 0   4 − (thỏa mãn). m =  3 Trang 3  4 − 
Vậy m  ;0thỏa mãn đề bài.  3  Câu 3.
(2,0 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol (P) 2
: y = 2x và đường thẳng
(d ): y = x + m (với m là tham số).
a) Tìm m để (d ) đi qua điểm A(2;8) .
b) Tìm m để (d ) cắt (P) tại hai điểm phân biệt có hoành độ x , x thỏa mãn: 1 2
x + x − 3x x = 5. 1 2 1 2 Lời giải
a) Đường thẳng (d ) : y = x + m đi qua điểm A(2;8)  2 + m = 8  m = 6 .
Vậy m = 6 thì (d ) đi qua điểm A(2;8) .
b) Xét phương trình hoành độ giao điểm của parabol (P) 2
: y = 2x và đường thẳng
(d ): y = x + m là: 2 2
2x = x + m  2x − x − m = 0 (*) .
Phương trình (*) có:  = (− )2
1 − 4.2.(−m) = 1+ 8m .
Để (d ) cắt (P) tại hai điểm phân biệt có hoành độ x , x thì phương trình (*) có hai nghiệm 1 2 1 −
phân biệt x , x    0  1+ 8m  0  m  . 1 2 8  1 x + x =  1 2 
Theo định lí Vi-et ta có: 2  −m x .x = 1 2  2 −m
Theo bài ra: x + x − 3x x = 1 5  − 3.
= 5  1+ 3m =10  3m = 9  m = 3(thỏa mãn). 1 2 1 2 2 2
Vậy m = 3 là giá trị cần tìm. Câu 4. (3,5 điểm)
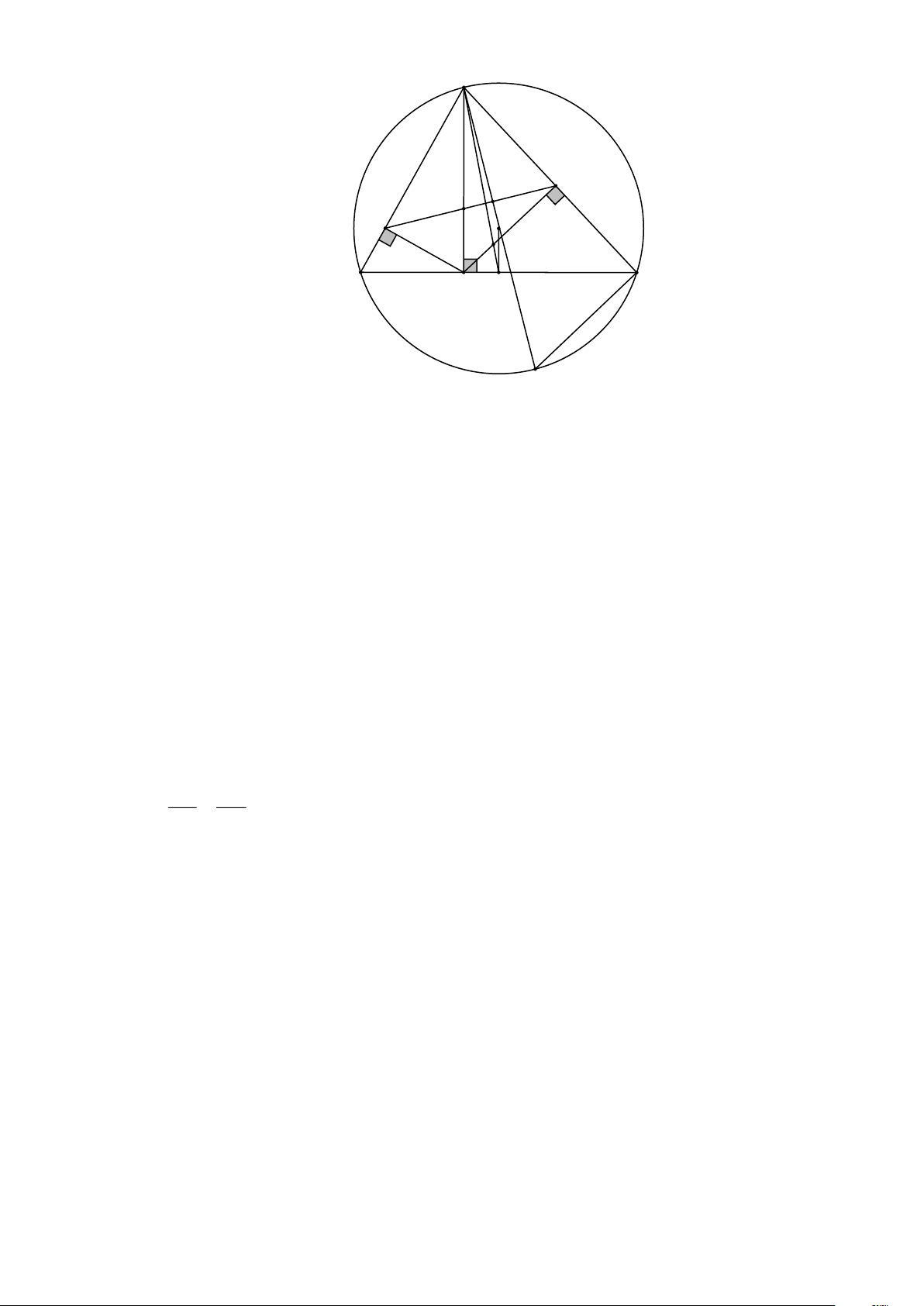
1) Cho tam giác ABC nhọn, nội tiếp đường tròn (O; R) . Kẻ AH vuông góc với BC tại H ,
HK vuông góc với AB tại K và HI vuông góc với AC tại I .
a) Chứng minh tứ giác AKHI nội tiếp đường tròn.
b) Gọi E là giao điểm của AH với KI . Chứng minh rằng .
EA EH = EK.EI .
c) Chứng minh KI vuông góc với AO .
d) Giả sử điểm A và đường tròn (O; R) cố định, còn dây BC thay đổi sao cho 2 . AB AC = 3R .
Xác định vị trí của dây cung BC sao cho tam giác ABC có diện tích lớn nhất.
2) Một hình nón có diện tích đáy bằng ( 2
16 cm ) và có chiều cao gấp ba lần bán kính đáy.
Tính thể tích của hình nón đó. Lời giải Trang 4 A 1 1 E J K O 1 2 B C H M 1 F
1. a) Chứng minh tứ giác AKHI nội tiếp đường tròn. Ta có:
AKH = 90 (vì HK vuông góc với AB tại K )
AIH = 90 (vì HI vuông góc với AC tại I ).
Xét tứ giác AKHI có: AKH + AIH = 90 + 90 = 180 , mà hai góc này ở vị trí đối nhau.
Vậy tứ giác AKHI nội tiếp đường tròn.
b) Gọi E là giao điểm của AH với KI . Chứng minh rằng .
EA EH = EK.EI .
Vì tứ giác AKHI nội tiếp đường tròn (cmt) nên HKI = HAI (hai góc nội tiếp cùng chắn HI ) Hay HKE = IAE .
Xét EKH và EAI có:
KEH = AEI (hai góc đối đỉnh);
HKE = IAE (cmt) Do đó: EK  H ∽ EAI  (g.g) EK EH  =  E .
A EH = EK.EI EA EI
Vậy ta có điều phải chứng minh.
c) Chứng minh KI vuông góc với AO .
Kẻ đường kính AF của đường tròn (O; R) . Gọi J là giao điểm của KI và AO .
Xét đường tròn (O; R) có F = B (hai góc nội tiếp cùng chắn cung AC ). ( ) 1 1 1
Lại có B = H (vì cùng phụ với H ). (2) 1 1 2
Vì tứ giác AKHI nội tiếp đường tròn (cmt)
nên H = I (hai góc nội tiếp cùng chắn cung AK ) (3) 1 1 Từ ( )
1 ; (2) và (3) suy ra: F = I . 1 1
Mà trong đường tròn (O; R) có: ACF = 90 (góc nội tiếp chắn nửa đường tròn).
Hay A + F = 90 (4) . 1 1
Từ (3) và (4) suy ra A + I = 90  AJI = 90 . 1 1
Vậy KI vuông góc với AO . Trang 5
d) Giả sử điểm A và đường tròn (O; R) cố định, còn dây BC thay đổi sao cho 2 . AB AC = 3R .
Xác định vị trí của dây cung BC sao cho tam giác ABC có diện tích lớn nhất.
Có ACF = 90 (góc nội tiếp chắn nửa đường tròn)
ABH = AFC (hai góc nội tiếp cùng chắn cung AC của đường tròn (O; R)
Xét AHB và ACF có:
AHB = ACF (90) ; ABH = AFC (cmt) 2 AH AB A . B AC 3R 3R Do đó: AH  B∽ ACF  (g.g)  =  AH = = = . AC AF AF 2R 2 1 1 3R 3R Ta có: S = AH.BC = . .BC = .BC . ABC 2 2 2 4
Do R không đổi nên S
lớn nhất  BC lớn nhất. ABC
Gọi M là trung điểm của BC thì OM ⊥ BC .
BC lớn nhất  OM bé nhất. 3R R
Ta có OM  AM − AO  AH − AO = − R = . 2 2 R OM bé nhất bằng  ,
A O, M thẳng hàng và H  M . 2 R 3R
Khi đó AH = AM = AO + OM = R + = . 2 2 3R
Vậy diện tích ABC lớn nhất khi BC cách A một khoảng bằng ( ABC đều) 2
2) Gọi bán kính đáy của hình nón là R .
Do diện tích của đáy hình nón là 2 S = 16  R  = 16  R = 4(cm)
Theo giả thiết chiều cao của hình nón gấp 3 lần bán kính đáy nên chiều cao của hình nón là:
h = 3R = 3.4 = 12(cm) 1 1
Thể tích hình nón là: V = S.h = .16 .1  2 =64( 3 cm ) 3 3
Vậy thể tích hình nón là 3 64 cm . Câu 5. (0,5 điểm)
Cho các số thực dương x, y, z thỏa mãn x + y + z = 6. Tìm giá trị lớn nhất của biểu thức 3 3 3 xy yz zx P = + + . 3 3 3
y + 4 z + 4 x + 4 Lời giải
Áp dụng bất đẳng thức AM – GM cho ba số dương ta có: 3 3 3 xy yz zx P = + + 3 3 3 3 3 3 y y z z x x + + 4 + + 4 + + 4 2 2 2 2 2 2 3 3 3 3 3 3 xy yz zx xy yz zx P  + + = + + 2 2 2 3 3 3 3 3 3 y y z z x x 3y 3z 3x 3 3 3 3. . .4 3. . .4 3. . .4 2 2 2 2 2 2
xy + yz + zx P  . 3 Trang 6
Lại có ( x − y)2 + ( y − z)2 + (z − x)2  0 x  , y, z 2 2 2
 x + y + z  xy + yz + zx
 (x + y + z)2  3(xy + yz + zx)
(x + y + z) 2 6
 xy + yz + zx  = =12 3 3 12  P  = 4 . 3
x = y = z Dấu “=” xảy ra khi 
 x = y = z = 2 .
x + y + z = 6
Vậy MaxP = 4  x = y = z = 2 .
---------------------------------@Hết@--------------------------------- Trang 7