Đề Thi Tuyển Sinh 10 Môn Toán Sở GD Thái Nguyên 2025-2026 Có Lời Giải

UBND TỈNH THÁI NGUYÊN
THI TUYỂN SINH LỚP 10
SỞ GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN
(Dành cho tất cả thí sinh) ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút, không kể thời gian giao đề
(Đề thi gồm có 01 trang, 10 câu, mỗi câu 1,0 điểm)
Câu 1. Không sử dụng máy tính cầm tay, rút gọn biểu thức A = 2 + 8 − 18 .
Câu 2. Không sử dụng máy tính cầm tay, giải phương trình 2
x − 3x + 2 = 0. 2x − 3y = 3
Câu 3. Không sử dụng máy tính cầm tay, giải hệ phương trình  . 2x + y = 7
Câu 4. Cho hàm số bậc nhất y = 2x + m , với m là tham số.
a. Hàm số đã cho đồng biến hay nghịch biến trên ? Vì sao?
b. Tìm giá trị của m để đồ thị hàm số đã cho đi qua điểm A(1;3) . x 4 8
Câu 5. Cho biểu thức B = − + , với x  0 . x + 2 x x + 2 x
a. Rút gọn biểu thức B .
b. Tính giá trị của biểu thức B khi x = 7 + 4 3 .
Câu 6. Cho hình chữ nhật có chu vi bằng 30 .
cm Nếu chiều rộng tăng thêm 3cm và chiều dài
giảm đi 1cm thì diện tích của hình chữ nhật đó sẽ tăng thêm 2
18cm . Tính chiều rộng và chiều dài
của hình chữ nhật đã cho.
Câu 7. Cho tam giác ABC vuông tại A có đường cao AH. Biết AH = 4cm và HC = 3c . m
Tính độ dài các đoạn thẳng AC, BC và . AB
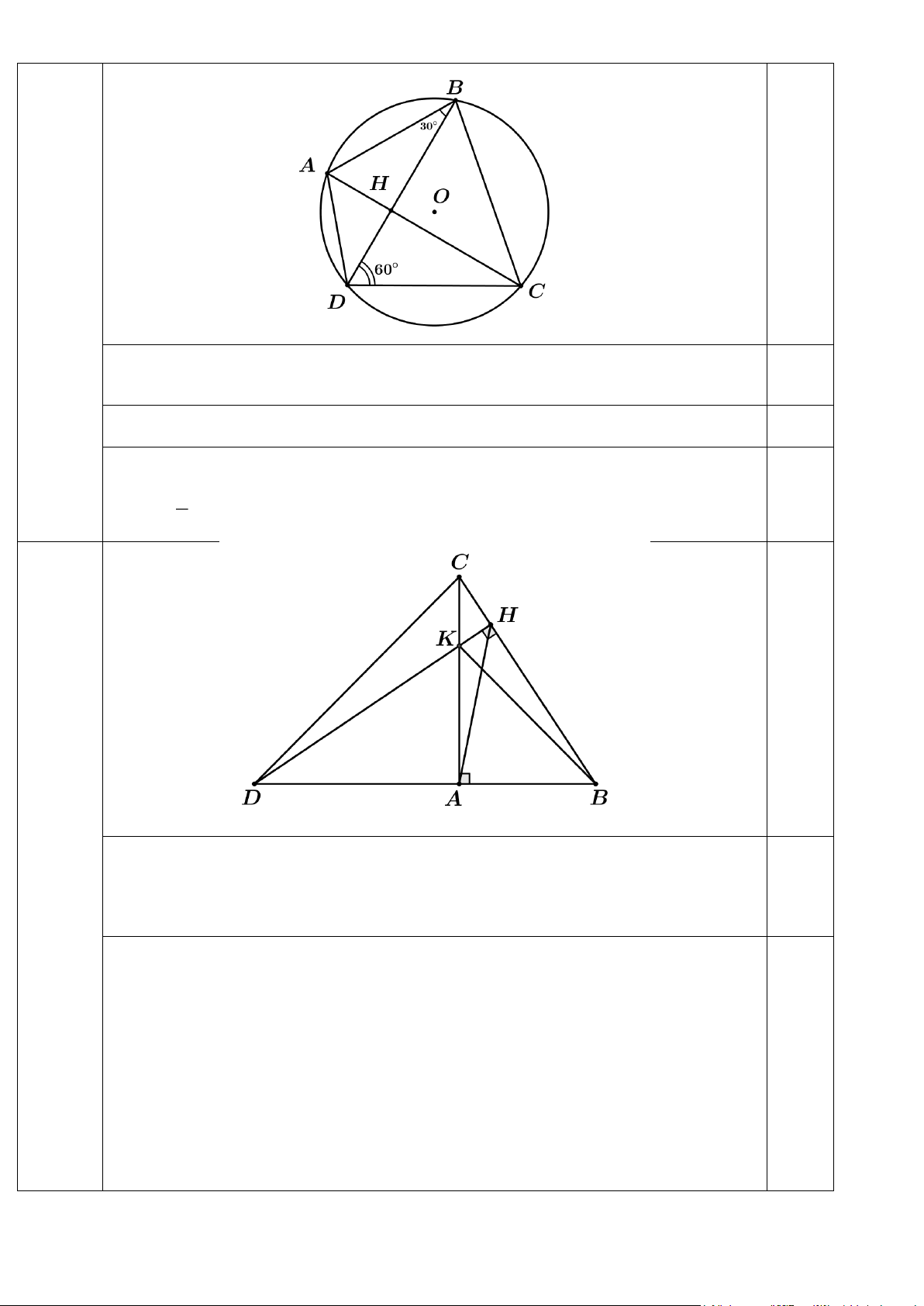
Câu 8. Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi H là giao điểm của hai đường chéo AC và .
BD Biết rằng ABD = 30 ,
 BDC = 60 . Tính số đo của các cung nhỏ AD, BC và số đo của BHC.
Câu 9. Cho tam giác ABC vuông tại A ( AC  AB). Trên tia BA lấy điểm D sao cho
AD = AC. Kẻ DH vuông góc với BC tại điểm H. Gọi K là giao điểm của hai đường thẳng
DH và AC. Chứng minh rằng: a. DHA = DC ; A b. AK = . AB
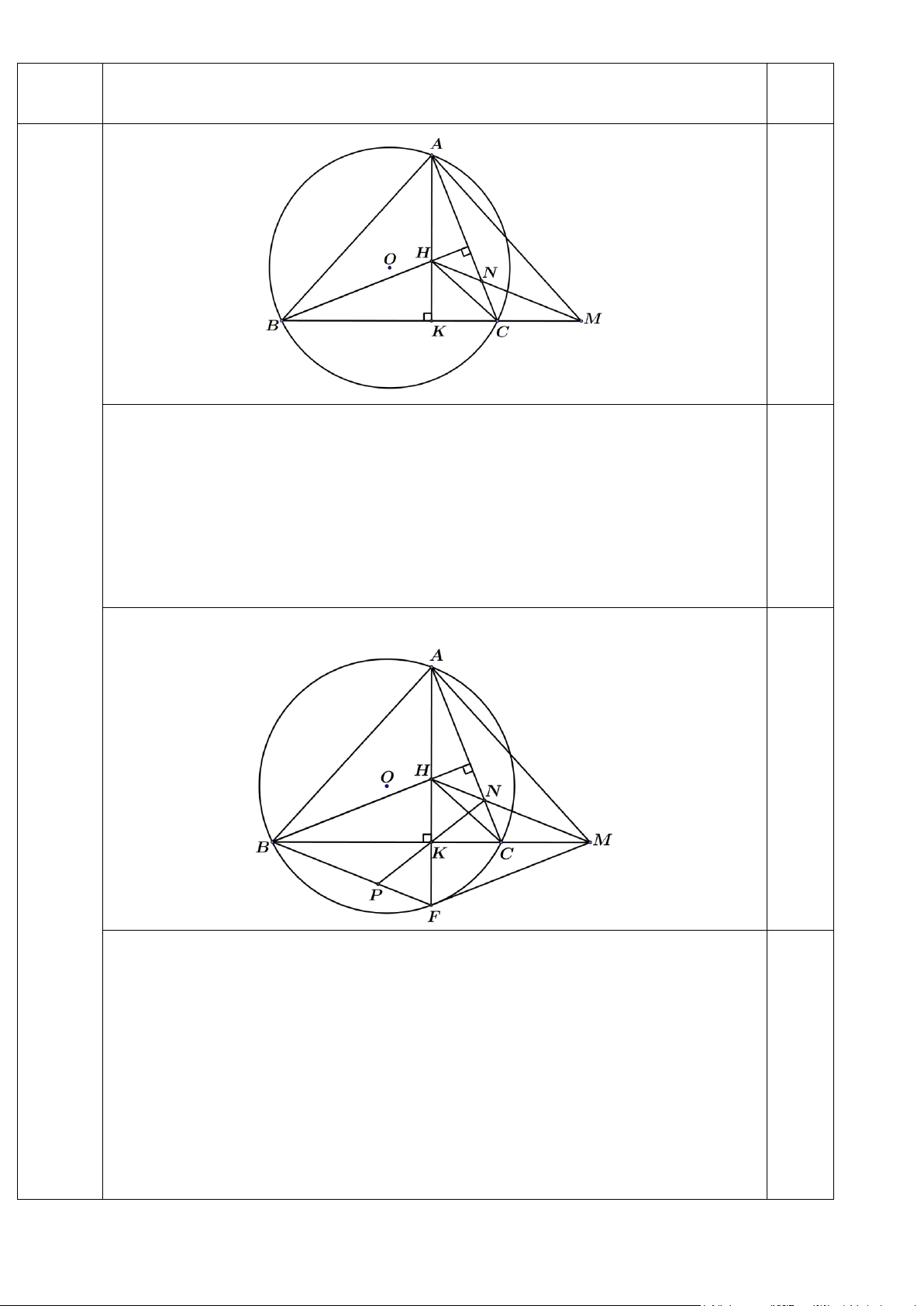
Câu 10. Cho tam giác ABC ( AB  BC  AC) có ba góc nhọn nội tiếp đường tròn (O). Gọi
điểm K là chân đường vuông góc kẻ từ điểm A đến cạnh BC và H là trực tâm của tam giác
ABC. Gọi M là điểm đối xứng với điểm B qua điểm K. Gọi điểm N là giao điểm của hai
đường thẳng HM và AC.
a. Chứng minh rằng bốn điểm ,
A H , C, M cùng thuộc một đường tròn.
b. Đường thẳng AH cắt đường tròn (O) tại điểm F (F  A).Gọi P là giao điểm của
hai đường thẳng KN và BF. Chứng minh rằng N . A NC = NM . . FP ------ HẾT ------
Họ và tên thí sinh:………………….……………................Số báo danh:……….………… Trang 1
UBND TỈNH THÁI NGUYÊN
THI TUYỂN SINH LỚP 10
SỞ GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN
(Dành cho tất cả thí sinh) ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút, không kể thời gian giao đề HƯỚNG DẪN CHẤM
( Bản hướng dẫn chấm gồm có 05 trang) I. Hướng dẫn chung
- Giám khảo cần nắm vững yêu cầu của hướng dẫn chấm để đánh giá đúng bài làm của
thí sinh. Thí sinh làm cách khác đáp án nếu đúng vẫn cho điểm tối đa.
- Khi vận dụng đáp án và thang điểm, giám khảo cần chủ động, linh hoạt với tinh thần
trân trọng bài làm của học sinh.
- Nếu có việc chi tiết hóa điểm các ý cần phải đảm bảo không sai lệch với tổng điểm và
được thống nhất trong toàn hội đồng chấm thi.
- Điểm toàn bài là tổng điểm của các câu hỏi trong đề thi, chấm điểm lẻ đến 0,25 và không làm tròn.
II. Đáp án và thang điểm Câu Nội dung Điểm A = 2 + 8 − 18 Câu 1 0.5 = 2 + 2 2 − 3 2 = 0 . 0.5
Ta có a + b + c = 1+ ( 3 − ) + 2 = 0 . 0.5 Câu 2
Do đó phương trình đã cho có hai nghiệm phân biệt x = 1; 1 0.25 x = 2. 2 0.25 2x − 3y = 3  4 − y = 4 −    0.5 2x + y = 7 2x + y = 7 y = 1   0.25 Câu 3 2x +1 = 7 x = 3   . y =1 0.25
Vậy hệ phương trình đã cho có nghiệm ( ; x y) = (3; ) 1 .
a. Hàm số y = 2x + m đồng biến trên . 0.5 Vì a = 2  0 . 0.25 Câu 4
b. Đồ thị hàm số y = 2x + m đi qua điểm A(1;3) khi và chỉ khi 0.25
3 = 2.1+ m  m = 1. Trang 2
x x − 4( x + 2) + 8
a. Với x  0 thì B = 0.25 x ( x + 2) x ( x − 4) = Câu 5 0.25 x ( x + 2) x − ( x −2)( x +2 4 ) = = = x − 2 . 0.25 x + 2 x + 2 b. Ta có x = + = ( + )2 7 4 3
3 2 . Khi đó B = ( + )2
3 2 − 2 = 3 + 2 − 2 = 3 . 0.25
Gọi chiều rộng, chiều dài của hình chữ nhật ban đầu lần lượt là x, y ( x, y  0), đơn vị: cm . 0.25
Khi đó ta có: 2( x + y) = 30  x + y = 15.
Khi chiều rộng tăng thêm 3cm và chiều dài giảm đi 1cm thì diện tích của hình
chữ nhật đó sẽ tăng thêm 2
18cm nên ta có phương trình: 0.25 Câu 6 (x + 3)( y − )
1 = xy +18  −x + 3y = 21.
Từ đó, ta có hệ phương trình: x + y = 15 x = 6   
(thoả mãn điều kiện). 0.25
−x + 3y = 21 y = 9
Vậy chiều rộng, chiều dài của hình chữ nhật ban đầu lần lượt là 6(cm);9(cm). 0.25 0.25
Áp dụng định lý Py-ta-go trong tam giác vuông AHC ta có: 2 2 2 2 2 2 0.25
AC = AH + HC  AC = 4 + 3 = 25  AC = 5(cm) . Câu 7
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: 2 2 AH 16
AH = BH.CH  BH = = (cm) . CH 3 0.25 16 25
Do đó BC = BH + CH = + 3 = (cm). 3 3
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: AH.BC 20 A .
B AC = AH.BC  AB = = (cm). 0.25 AC 3 Trang 3 0.25 Câu 8
Áp dụng định lý của góc nội tiếp ta có: 0.25
sđ AD = 2ABD = 6  0 .
sđ BC = 2BDC = 12  0 . 0.25
Vì BHC là góc có đỉnh ở bên trong đường tròn nên ta có: 0.25
BHC = 1(s®AD+s®BC) = 9  0 . 2 0.25 DHA DCA Câu 9 a. Chứng minh = . Vì CAD = CHD = 
90 (giả thiết) nên tứ giác AHCD là tứ giác nội tiếp đường tròn. 0.25
Suy ra DHA = DCA (hai góc nội tiếp cùng chắn AD ).
b. Chứng minh AK = A . B AC =  AD Vì 
nên ACD vuông cân tại . A DAC =  90
Suy ra DHA = DCA = 4  5 . (1) 0.25 Vì KAB = KHB = 
90 (giả thiết) nên KAB + KHB = 18  0 .
Do đó, tứ giác AKHB là tứ giác nội tiếp đường tròn.
Suy ra KBA = KHA (hai góc nội tiếp cùng chắn AK ). (2)
Từ (1), (2) suy ra KBA = 4  5 . Trang 4 Do đó AKB = 9  0 − 4  5 = 4  5 . 0.25
Vậy tam giác ABK vuông cân tại .
A Suy ra AK = A . B 0.25
a. Chứng minh rằng bốn điểm ,
A H , C, M cùng thuộc một đường tròn. HK ⊥ BM Theo giả thiết ta có:  .
K lµ trung ®iÓm cña BM 0.25
Suy ra HBM cân tại H. Suy ra HBC = HM . C
Mặt khác HBC = HAC (hai góc cùng phụ với ACB).
Do đó HAC = HM .
C Suy ra bốn điểm ,
A H , C, M cùng thuộc một đường tròn.
b. Chứng minh rằng N . A NC = NM. . FP Câu 10 FBC = 
FAC (hai gãc néi tiÕp cï ng ch¾n FC) Ta có:  . FAC = 
HBC (hai gãc cï ng phô ví i AC B )
Suy ra HBK = KBF.
HBF có BK đồng thời là đường cao và đường phân giác. 0.25
Suy ra HBF cân tại B. Do đó KH = KF.
Vì tứ giác HBFM có hai đường chéo vuông góc với nhau tại trung điểm mỗi
đường nên tứ giác HBFM là hình thoi. Suy ra NHK = K . FP Trang 5 KHN = KFP 
Xét KHN và KFP ta có: KH = KF . HKN =  FKP (®èi ®Ønh)
Suy ra KHN = KFP ( . g . c ) g . Do đó HN = F . P
HAN = CMN (tø gi¸c AHCM néi tiÕp) Vì 
ANH = MNC (®èi ®Ønh)
nên ANH đồng dạng với MNC( . g g). 0.25 AN NH Suy ra =
 AN.NC = NH.MN. MN NC
Vì HN = FP nên N . A NC = NM. . FP ĐIỂM TOÀN BÀI 10,0 ---- Hết--- Trang 6