Đề Thi Tuyển Sinh 10 Môn Toán Sở GD Thanh Hóa 2025-2026 Có Lời Giải

SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THANH HÓA
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Câu 1. (2,0 điểm) x x +1 2 + 5 x Cho biểu thức P = + −
vơi x  0, x  4 . x + 2 x − 2 x − 4
1. Rút gọn biểu thức P .
2. Tìm tất cả các giá trị của x để P  1 . Câu 2. (2,0 điểm)
1. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d ) có phương trình y = ax + b . Tìm
a,b để đường thẳng (d ) có hệ số góc bằng 3 và đi qua điểm M ( 1 − ;2) . 3  x + y = 6
2. Giải hệ phương trình  . x − y = 2 − Câu 3. (2,0 điểm) 1. Giải phương trình 2
x − 3x + 2 = 0 . 2. Cho phương trình 2 2
x − 2mx − m − 2 = 0 ( m là tham số). Tìm các giá trị của m để
phương trình có hai nghiệm x , x (với x  x ) thỏa mãn hệ thức 1 2 1 2 2
x − 2 x − 3x x = 3m + 3m + 4 . 2 1 1 2 Câu 4. (3,0 điểm)
Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ điểm M kẻ hai tiếp tuyến M ,
A MB đến (O) (với ,
A B là các tiếp điểm). Gọi C là điểm đối xứng với B qua
O , đường thẳng MC cắt đường tròn (O) tại D (D khác C) .
1. Chứng minh MAOB là tứ giác nội tiếp.
2. Gọi N là giao điểm của hai đường thẳng AD và MO . Chứng minh 2 MN = N . D NA . 2 3. Gọi  HA  AC
H là giao điểm của MO và AB . Chứng minh − =1   .  HD  HN Câu 5. (1,0 điểm)
Cho các số thực không âm x, y, z thỏa mãn 2 2 2
4x + y + 4z  6y .
Tìm giá trị nhỏ nhất của biểu thức 8 16 1 M = + + + 2023 . 2 2 2 (x + 3) ( y + 4) (z +1)
---------------------------------49Hết49--------------------------------- Trang 1 HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm) x x +1 2 + 5 x Cho biểu thức P = + −
vơi x  0, x  4 . x + 2 x − 2 x − 4
1. Rút gọn biểu thức P .
2. Tìm tất cả các giá trị của x để P  1 . Lời giải x x +1 2 + 5 x 1) P = + − ; x 0 … , x  4 x + 2 x − 2 x − 4
x ( x − 2) + ( x + )
1 ( x + 2) −(2 + 5 x ) P = ( x + 2)( x − 2)
x − 2 x + x + 2 x + x + 2 − 2 − 5 x P = ( x + 2)( x − 2) 2x − 4 x P = ( x + 2)( x − 2) 2 x ( x − 2) P = ( x + 2)( x − 2) 2 x P = x + 2 2 x Vậy với x 0
… ; x  4 thì P = x + 2 2 x
2) Để P  1 ta có 1 với x 0 … ; x  4 x + 2 2 x  −1  0 x + 2 2 x − x − 2   0 x + 2 x − 2   0 x + 2 Do x 0 … nên x + 2 2
… , tức x + 2  0
 x − 2  0  x  2  x  4 . Trang 2
kết hợp với điều kiện ta có x  4 .
Vậy x  4 ,thì P  1 Câu 2. (2,0 điểm)
1.Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d ) có phương trình y = ax + b . Tìm
a,b để đường thẳng (d ) có hệ số góc bằng 3 và đi qua điểm M ( 1 − ;2) . 3  x + y = 6
2.Giải hệ phương trình  . x − y = 2 − Lời giải
1) Phương trình đường thẳng (d ) : y = ax + b(a  0)
Vì d có hệ số góc bằng 3 nên a = 3  y = 3x + b
Vì d đi qua điểm M ( 1 − , 2)  3.(− )
1 + b = 2  b = 5
Vậy a = 3;b = 5 3  x + y = 6 4 x = 4 x =1 2) Ta có      x − y = 2 − x − y = 2 − y = 3
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (1;3) Câu 3. (2,0 điểm) 1.Giải phương trình 2
x − 3x + 2 = 0 . 2.Cho phương trình 2 2
x − 2mx − m − 2 = 0 ( m là tham số). Tìm các giá trị của m để
phương trình có hai nghiệm x , x (với x  x ) thỏa mãn hệ thức 1 2 1 2 2
x − 2 x − 3x x = 3m + 3m + 4 . 2 1 1 2 Lời giải 1.Giải phương trình 2
x − 3x + 2 = 0 . Ta có 2 2
Δ = b − 4ac = ( 3 − ) − 4 2 = 1  0  3 + 1 x = = 2 1 
Nên phương trình có hai nghiệm phân biệt 2   3 − 1 x = = 1 2  2
Vậy tập nghiệm của phương trình là S = 1;  2 . 2.Ta có 2
a c = −m − 2„ − 2  0 nên phương trình có hai nghiệm trái dấu
mà x  x nên x  0  x  x = −x 1 2 1 2 1 1
x + x = 2m Theo Vi-ét ta có 1 2  2 x x = −m − 2  1 2 Theo bài ra 2
x − 2 x − 3x x =3m + 3m + 4 2 1 1 2 Trang 3
 x + 2x − 3( 2 −m − 2) 2 = 3m + 3m + 4 2 1
 2x + x = 3m − 2 kết hợp với x + x = 2m 1 2 1 2 x = m − 2 1   mà 2
x  x = −m − 2 x = m + 2  1 2 2
 (m − )(m + ) 2 2 2 = −m − 2 2 2 2
m − 4 + m + 2 = 0  2m = 2
 m = 1 ( thỏa mãn)
Vậy m = 1 là giá trị cần tìm Câu 4. (3,0 điểm)
Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ điểm M kẻ hai tiếp tuyến M ,
A MB đến (O) (với ,
A B là các tiếp điểm). Gọi C là điểm đối xứng với B qua
O , đường thẳng MC cắt đường tròn (O) tại D (D khác C) .
1.Chứng minh MAOB là tứ giác nội tiếp.
2.Gọi N là giao điểm của hai đường thẳng AD và MO . Chứng minh 2 MN = N . D NA . 2 3.Gọi  HA  AC
H là giao điểm của MO và AB . Chứng minh: − =1   .  HD  HN Lời giải
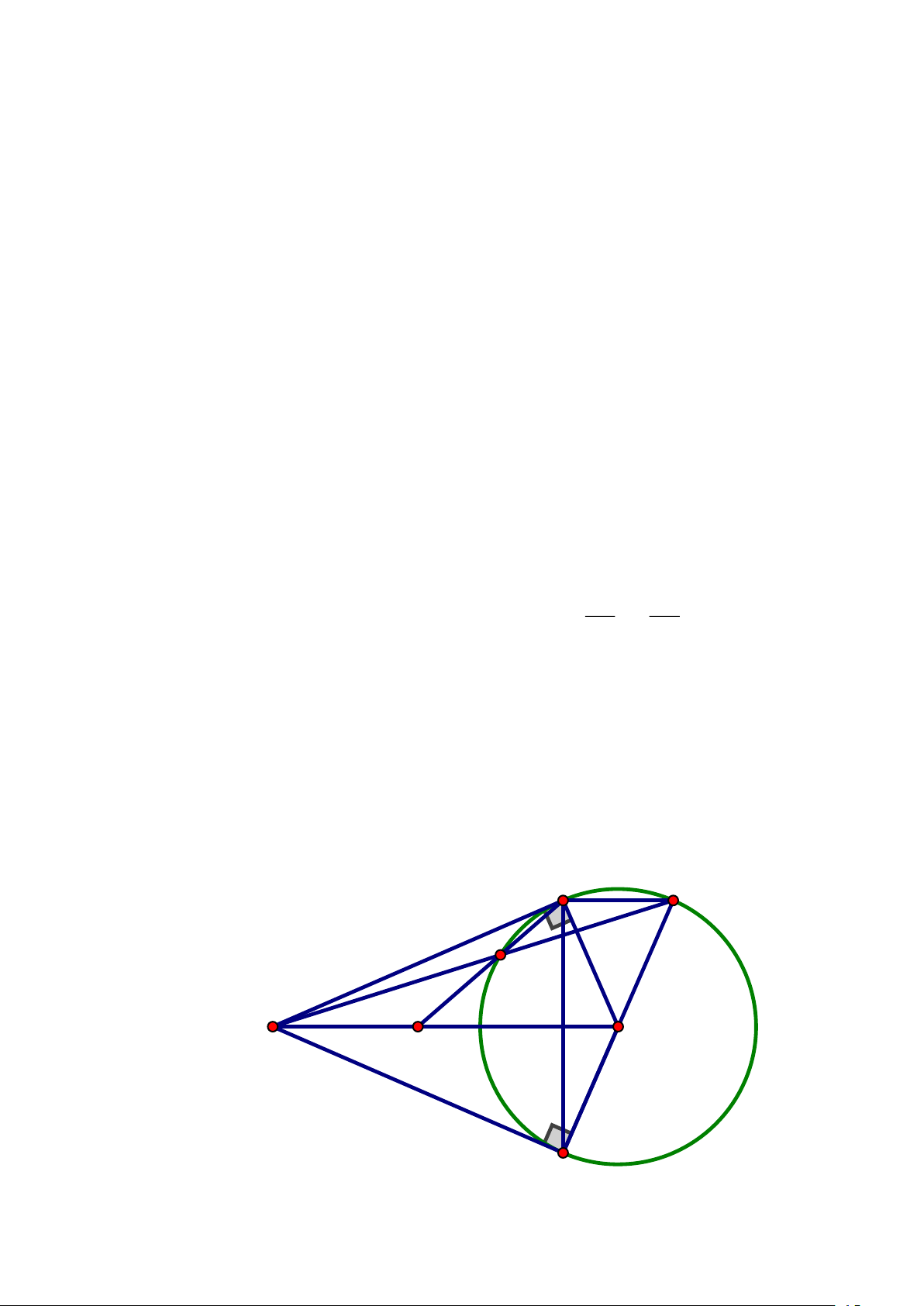
1) Chứng minh MAOB là tứ giác nội tiếp
- Có MAO = MBO = 90 ( Do M ,
A MB là các tiếp tuyến của (O) tại A và B )
Xét tứ giác MAOB có MAO + MBO = 90 + 90 = 180
mà hai góc này đối nhau nên tứ giác MAOB nội tiếp đường tròn đường kính MO . A C D M O N B 2) Chứng minh 2 MN = . ND NA Trang 4
Có BAC = 90 ( Góc nội tiếp chẳn nửa đường tròn)  AC ⊥ AB (1)
MA = MB ( tính chất 2 tiếp tuyến cắt nhau) OA = OB ( bán kính của (O) )
Nên MO là trung trực của đoạn thẳng AB  MO ⊥ AB (2)
Từ (1) và (2) suy ra AC // MO  NMD = ACD
mà MAN = ACD ( góc tạo bởi tia tiếp tuyến và dây và góc nội tiếp cùng chắn AD )  NMD = NAM
Xét NMD và NAM có: NMD = NAM và MNA chung Do đó NM  D∽ NA 
M ( g.g ) MN ND 2  =  MN = N . D NA NA MN Vậy 2 MN = . ND NA . 2 HA AC
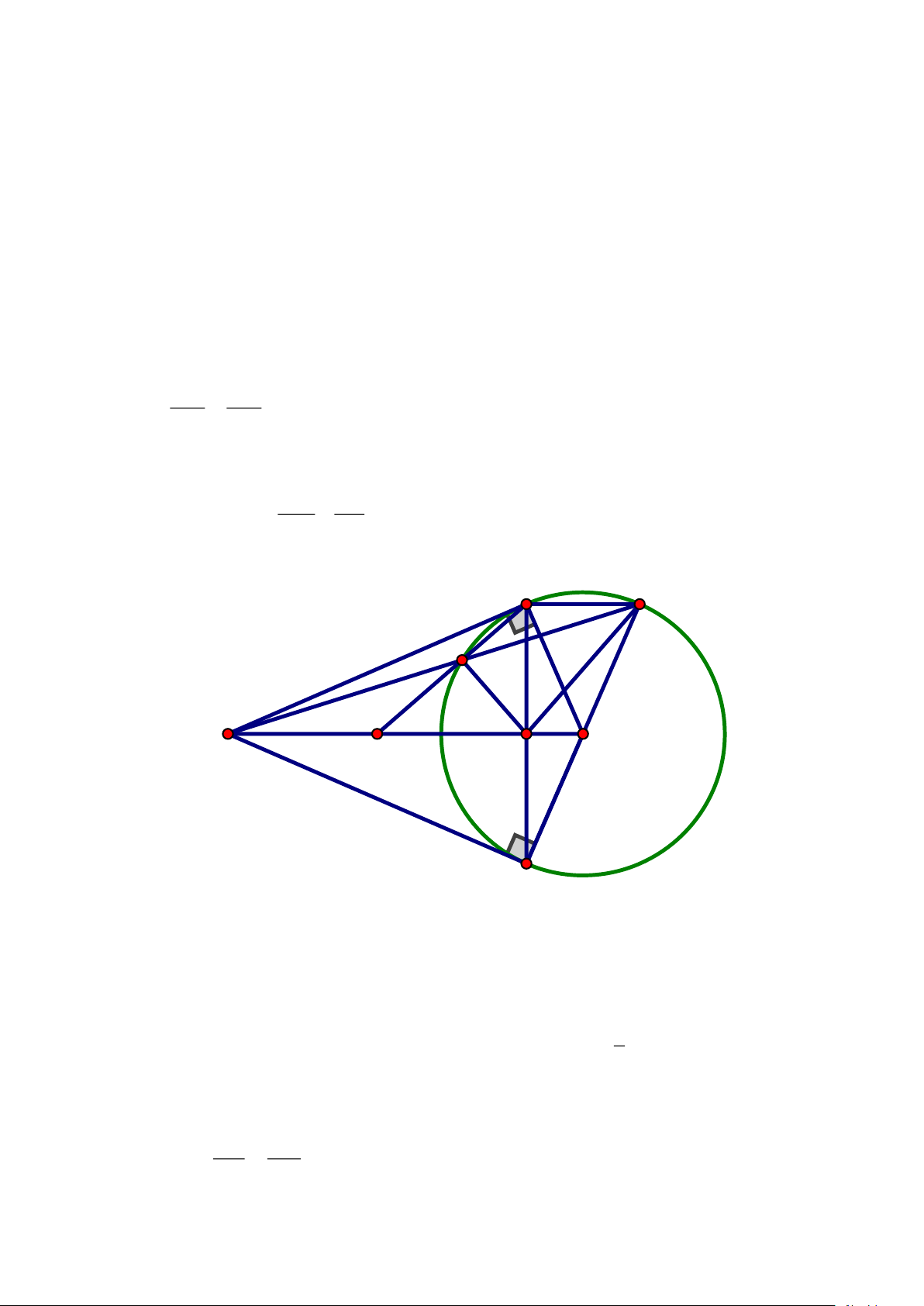
3. Chứng minh: - = 1. 2 HD HN A C D M O N H B Vì M ,
A MB là hai tiếp tuyến cắt nhau kẻ từ M đến đường tròn (O) nên MA = MB , và
MA là tia phân giác của góc AMB
Xét MAB cân tại M có MH là đường phân giác đồng thời là đường cao
Xét D MAD và DMCA có: · AMC chung ; · · 1 MDA = MCA = sđ »
AD ( góc nội tiếp và góc 2
tạo bởi tiếp tuyến và dây cung cùng chắn » AD )
Suy ra: DMAD∽DMCA (g.g) MD MA Do đó: 2 = Û M . D MC = MA MA MH
Suy ra: Tứ giác DHOC nội tiếp. Trang 5 · · · ·
Þ MHD = OCD = ODC = OHC · · 1 · 1 · · Þ DHA = AHC = DHC =
DOC = DBC ( mối quan hệ giữa góc nội tiếp và góc ở 2 2 tâm). Mà · ·
DAH = DCB nên · · · ·
DHA+ DAH = DBC + DCB = 90° · Þ ADH = 90° .
Xét D AHN vuông tại H có HD là đường cao nên 2 2 NH = N .
D NA = NM Þ NH = NM . 2 HA A . D AN AN Mặt khác = = ( ) 1 2 HD A . D DN DN AC AC AD Và = = (2) . HN MN DN 2 HA AC AN AD Từ (1) và (2) suy ra: - = - = 1 (đpcm). 2 HD HN DN DN
Câu 5. (1,0 điểm) Cho các số thực không âm x, y, z thỏa mãn 2 2 2
4x + y + 4z  6y .
Tìm giá trị nhỏ nhất của biểu thức 8 16 1 M = + + + 2023 . 2 2 2 (x + 3) ( y + 4) (z +1) Lời giải
Áp dụng bất đẳng thức Cô si ta được: 2 2 2 x +1  2 ;
x y + 4  8y; z +1  2z y 2 2 2
 8x + 8y + 8z  4x + y + 4z + 24 = 6y + 24  x + + z  3 4 Với hai số 1 1 8
a,b  0 thì ta có đánh giá cơ bản: +  * 2 2 2 ( ) a b (a +b) Áp dụng (*) ta được: 16 1 1 1 8 + = +  ( y + 4)2 ( z + )2 2 1  y  (z + )2 2 1  y  +1 + z + 2      4   4  8 8 64 +   1 (x +3)2 2 2  y   y  + z + 2 x + + z + 5      4   4 
Từ đó suy ra: M  2024
Vậy giá trị nhỏ nhất của M là 2024 khi (x, y, z) = (1,4, ) 1 .
---------------------------------49Hết49--------------------------------- Trang 6