Đề Thi Tuyển Sinh 10 Môn Toán Sở GD TP Hồ Chí Minh 2025-2026 Có Lời Giải

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT
THÀNH PHỐ HỒ CHÍ MINH Môn thi: Toán
Thời gian làm bài: 120 phút (Không tính thời gian phát đề) ĐỀ CHÍNH THỨC
(Đề thi gồm 02 trang) 2 x
Câu 1. (1,5 điểm) Cho parabol (P) : y =
và đường thẳng (d ) : y = x + 4 2
a) Vẽ đồ thị (P) và (d ) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép tính.
Câu 2. (1,0 điểm) Cho phương trình 2
2x −13x − 6 = 0 có 2 nghiệm là x ; x . Không giải phương trình, hãy 1 2
tính giá trị của biểu thức 2
A = (x + x ).(x + 2x ) − x 1 2 1 2 2
Câu 3. (0,75 điểm)
Một nhà khoa học đã đưa ra công thức tính số cân nặng lý tưởng của con người theo chiều cao và giới tính T −150
như sau: M = T −100 − N
Trong đó M là cân nặng (kg), T là chiều cao (cm), N = 4 nếu là nam, N = 2 nếu là nữ.
a) Bạn Hạnh (nữ) cao 1,58 mét. Hỏi cân nặng lý tưởng của bạn Hạnh là bao nhiêu?
b) Bạn Phúc (nam) có cân nặng 68 kg. Để cân nặng này là lý tưởng thì chiều cao cần đạt của bạn Phúc là bao nhiêu?
Câu 4. (0,75 điểm)
Cửa hàng A niêm yết giá một bông hồng là 15000 đồng. Nếu khách hàng mua nhiều hơn 10 bông thì từ
bông thứ 11 trở đi, mỗi bông được giảm 10% trên giá niêm yết. Nếu mua nhiều hơn 20 bông thì từ bông
thứ 21 trở đi, mỗi bông được giảm thêm 20% trên giá đã giảm.
a) Nếu khách hàng mua 30 bông hồng tại cửa hàng A thì phải trả bao nhiêu tiền?
b) Bạn Thảo đã mua một số bông hồng tại cửa hàng A với số tiền là 555000 đồng. Hỏi bạn Thảo đã mua bao nhiêu bông hồng?
Câu 5. (1,0 điểm)
Chị Lan đun sôi nước bằng ấm điện. Biết rằng mối liên hệ giữa công suất hao phí P (W ) của ấm điện và thời
gian đun t (giây) được mô hình hóa bởi một hàm số bậc nhất có dạng P = at + b và có đồ thị như hình bên.
a) Hãy xác định các hệ số a và b .
b) Nếu đun nước với công suất hao phí là 105(W ) thì thời gian đun là bao lâu?
Câu 6. (1,0 điểm)
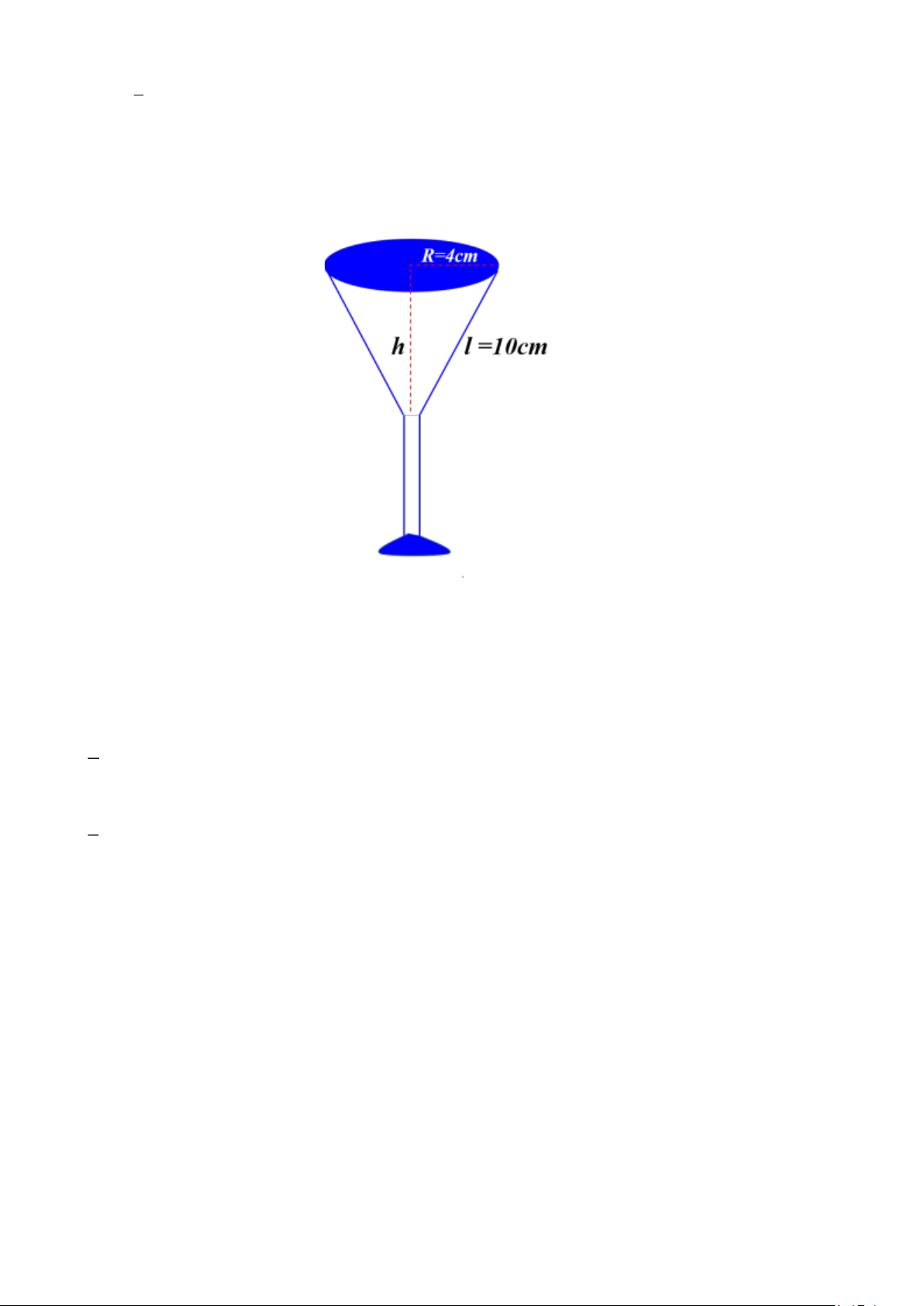
Bạn Nam dự định tổ chức buổi tiệc sinh nhật và chọn loại ly có phần chứa nước dạng hình nón với bán kính đáy
R = 4cm và độ dài đường sinh
l = 10cm để khách uống nước trái cây. Trang 1
a) Tính thể tích phần chứa nước của ly (ghi kết quả làm tròn đến hàng đơn vị). Biết công thức thể tích hình 1 nón là: 3
V =  R (với R là bán kính đáy hình nón; h là chiều cao hình nón). 3
b) Bạn Nam cần chuẩn bị một số hộp nước trái cây có lượng nước trong mỗi hộp là 1, 2 lít. Biết rằng buổi
tiệc sinh nhật có 14 người (đã bao gồm Nam). Nếu mỗi người trung bình uống 3 ly nước trái cây và lượng
nước rót bằng 90% thể tích ly thì bạn Nam cần chuẩn bị ít nhất bao nhiêu hộp nước trái cây? Biết 1 lít = 3 1000 cm .
Câu 7. (1,0 điểm)
Nhà bạn Khanh có hai thùng đựng sữa, thùng thứ nhất có thể tích 10 lít, thùng thứ hai có thể tích 8 lít. Biết
rằng cả hai thùng đều đang chứa một lượng sữa và tổng lượng sữa ở hai thùng lớn hơn 10 lít. Bạn Khanh
muốn xác định lượng sữa ở mỗi thùng nhưng không có dụng cụ đo thể tích nên bạn đã nghĩ ra cách làm như sau:
Đầu tiên, Khanh đổ sữa từ thùng thứ nhất sang thùng thứ hai cho đầy thì lượng sữa còn lại ở thùng thứ nhất 1
bằng lượng sữa so với ban đầu. 2
Sau đó, Khanh đổ sữa từ thùng thứ hai sang thùng thứ nhất cho đầy thì lượng sữa còn lại ở thùng thứ hai 1
bằng lượng sữa so với thời điểm ban đầu. 5
Hỏi thời điểm ban đầu mỗi thùng chứa bao nhiêu lít sữa?
Câu 8. (3,0 điểm)
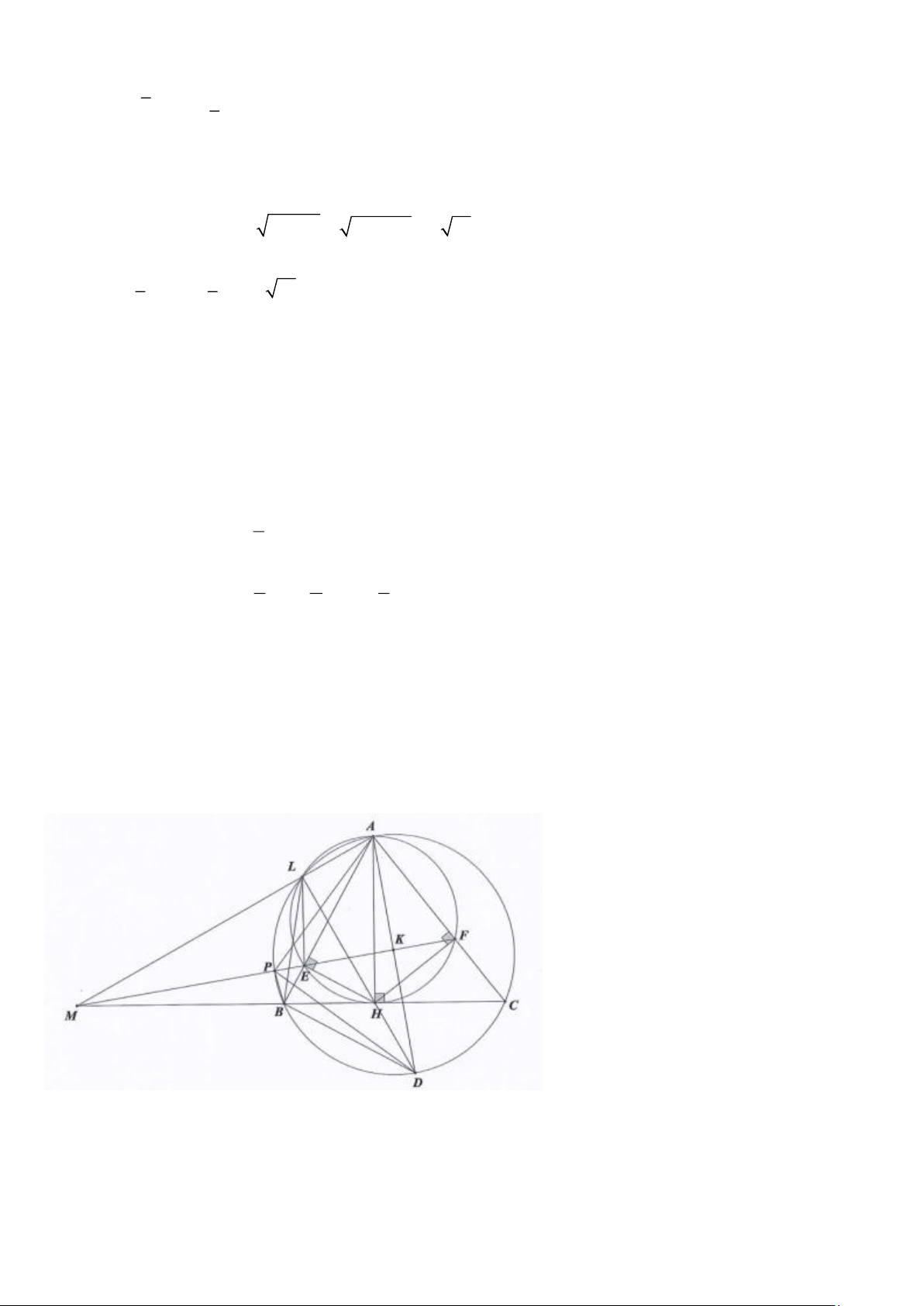
Cho tam giác ABC nhọn ( AB  AC) có đường cao AH và nội tiếp đường tròn (O) . Gọi E, F lần lượt là
hình chiếu của H lên các cạnh AB, AC . Đường kính AD của (O) cắt EF tại K và DH cắt (O) tại L ( L khác D ).
a) Chứng minh các tứ giác AEHF và ALHF nội tiếp.
b) Chứng minh tứ giác BEFC nội tiếp và AD vuông góc với EF tại K .
c) Tia EF cắt (O) tại P và cắt BC tại M . Chứng minh AP = AH và ba điểm ,
A L, M thẳng hàng. ---HẾT--- Trang 2 ĐÁP ÁN Bài 1. a) Thí sinh tự vẽ.
b) Phương trình hoành độ giao điểm của (P) và (d ) là 2 x 2
= x + 4  x − 2x −8 = 0  x = 2 − hay x = 4 − . 2
Vậy tọa độ giao điểm của (P) và (d) là ( 2 − , 2),(4,8). Bài 2.
Theo hệ thức Vi ét ta có b 13 x + x = − = 1 2 a 2 c x .x = = 3 − 1 2 a Ta có
A = ( x + x )( x + 2x ) − x = x + 3x x + x = (x + x )2 2 2 2 + x x 1 2 1 2 2 1 1 2 2 1 2 1 2 2 13  157 = − 3 = .    2  4 Bài 3.
a) Cân nặng lý tưởng của Huyền là 158 −150 M = 158 −100 − = 54(kg). 2
b) Chiều cao lý tưởng của bạn Phúc thỏa mãn T −150 68 = T −100 −
 3T = 68 4 + 400 −150 = 522  T =174(cm). 4
Vậy Phúc cần cao 1,74m Bài 4:
a) Số tiền mua 30 bông hoa là
10.15000 +10.15000.90% +10.15000.90%.80% = 393000 (đồng)
b) Vì số tiền mua bông của bạn Thảo lớn hơn 393000 nên số bông của bạn Thảo đã mua nhiều hơn 30
bông. Gọi x ( x là số tự nhiên lớn hơn 30) là số bông của bạn Thảo đã mua. Ta có phương trình
10.15000 +10.15000.90% + ( x − 20).15000.90%.80% = 555000  x = 45 .
Vậy bạn Thảo mua 45 bông hoa. 555000 − 393000
Cách khác: số hoa chênh lệch giữa hai bạn là =15 . Tức là, 15000.0,9.0,8 Thảo đã mua 45 bông hoa. Bài 5: a) Theo đồ thị ta có P  ( )  1
75 = 75a + b = 110 a =    P  (180) 3 . =180a + b =145 b  = 85 Trang 3
b) Thời gian đun thỏa mãn  1 a = 1 
3 .105 = t + 85  t = 60 giây. 3 b  = 85
Vậy cần 60 giây để đun nước. Bài 6: a) Độ cao của ly là 2 2
h = l − R = 100 −16 = 2 21(cm). Thể tích ly là 1  2 2
V =  R h = .4 .2 21 154( 3 cm ) . 3 3
b) Lượng nước trái cây cần chuẩn bị cho 14 khách là 3
154.14.3.0,9 = 5821, 2(cm ) Vì 5821, 2:1200 = 4,851
Nên bạn Nam cần chuẩn bị ít nhất 5 hộp nước trái cây. Bài 7:
Gọi x và y lần lượt là số lít sữa trong thùng 1 và 2 . Ta có các điều kiện 0  x  10,0  y  8, x + y  10 . 1
Trong lần đổ thứ nhất ta có x + y = 8 . 2 x y 4
Trong lần thứ hai ta có 10 − = 8 −
 x + y = 10 . 2 5 5
Vậy ta có x = 6, y = 5 .
Vậy tức là thùng 1 ban đầu có 6 lít và thùng 2 có 5 lít. Bài 8:
a) Chứng minh tứ giác AEHF và ALHF nội tiếp
Ta có góc AEH = AFH = 90 (Do E, F lần lượt là hình chiếu của H lên AB và AC )
Nên góc AEH + AFH = 180 . Trang 4
Và do đó tứ giác AEHF nội tiếp đường tròn đường kính AH
Ta có góc ALH + ALD = 90 (góc nội tiếp chắn nửa đường tròn) Mà góc AFH = 90
Nên góc ALH + AFH = 180
Vậy tứ giác ALHF nội tiếp trong đường tròn đường kính AH.
b) Chứng minh tứ giác BEFC nội tiếp và AD vuông góc với EF tại K .
AEF = AHF (tứ giác AEHF nội tiếp)
AHF = ACH (cùng phụ với HAC) .
Suy ra AEF = ACH = ACB  tứ giác BEFC nội tiếp. 1
Vì tứ giác BEFC nội tiếp  AEK = ACB = sd AB . 2 1 EAK = sd BD 2 1 1 1
 AEK + EAK = sd AB + sd BD = sd AD = 90 2 2 2
Suy ra AKE = 90 hay AD ⊥ EF tại K .
c) Chứng minh AP = AH và ba điểm ,
A L, M thẳng hàng
Xét tam giác AHB vuông tại H có đường cao HE : 2
AH = AE.AB (1)
Ta có APK = ADP (cùng phụ PAD )
ADP = ABP (cùng chắn AP )  APK = ABP
Chứng minh được tam giác APE đồng dạng tam giác ABP 2
 AP = AE.AB (2)
Từ (1) và (2) suy ra AP = AH
Ta có tứ giác ALEF nội tiếp  MEL = LAF
Tứ giác ALBC nội tiếp  MBL = LAF
Suy ra MEL = MBL nên tứ giác MBEL nội tiếp
 MLE = EBC = AFE = 180 − ALE
MLE + ALE = 180 Vậy ,
A L, M thẳng hàng. Trang 5