






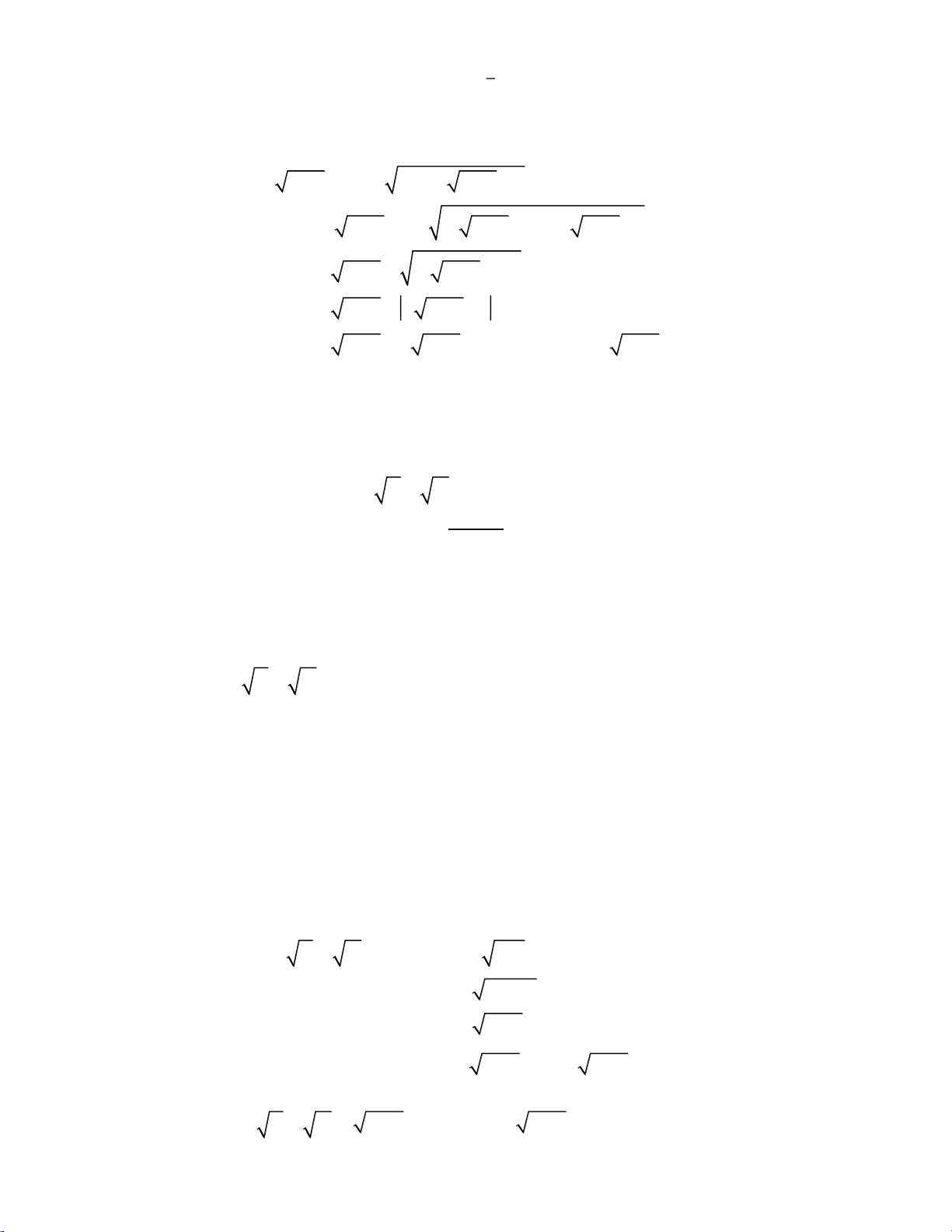





























Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 TỈNH AN GIANG
Năm học: 2021 - 2022
Môn thi: TOÁN - CHUYÊN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 150 phút
(Không kể thời gian phát đề) Bài 1. (3,0 điểm) a) Rút gọn A
419 40 19 419 40 19 . b) Giải phương trình 2
2x 2 3 3 x 3 3 0 .
c) Biết nghiệm của phương trình 2
2x 2 3 3 x 3 3 0 là nghiệm của phương trình 4 2
4x bx c 0 . Tìm các số b, c . Bài 2. (2,0 điểm)
a) Vẽ đồ thị P của hàm số 2 y x .
b) Viết phương trình đường thẳng d đi qua điểm A0;
1 và tiếp xúc với P . Bài 3. (1,0 điểm)
Cho hai số a, b phân biệt thỏa mãn 2 2
a 2021a b 2021b c , với c là một số thực dương. 1 1 2021 Chứng minh rằng: 0 . a b c Bài 4. (2,0 điểm)
Cho tam giác ABC ( AB AC ) nội tiếp trong đường tròn O đường kính AC . Gọi I là một
điểm thuộc đoạn OC ( I khác O và C ). Qua I kẻ đường vuông góc với AC cắt BC tại E và AB
kéo dài tại D . Gọi K là điểm đối xứng của C qua điểm I .
a) Chứng minh rằng các tứ giác BDCI và AKED nội tiếp. b) Chứng minh I . C IA I . E ID . Bài 5. (1,0 điểm)
Cho tam giác ABC đều có diện tích 2
36 cm . Gọi M , N , P là ba
điểm lần lượt nằm trên ba cạnh
AB, BC, CA sao cho
MN BC; NP AC; PM AB . Chứng tỏ rằng tam giác MNP đều
và tính diện tích tam giác MNP . Bài 6. (1,0 điểm)
Hai ngọn nến hình trụ có chiều cao và đường kính khác nhau được
đặt thẳng đứng trên mặt bàn. Ngọn nến thứ nhất cháy hết trong 6 giờ,
ngọn nến thứ hai cháy hết trong 8 giờ. Hai ngọn nến được thắp sáng cùng
lúc, sau 3 giờ chúng có cùng chiều cao.
a) Tìm tỉ lệ chiều cao lúc đầu của hai ngọn nến.
b) Biết tổng chiều cao của hai ngọn nến là 63 cm. Tính chiều cao của mỗi ngọn nến.
= = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = = Hướng dẫn giải: Bài 1. (3,0 điểm) a) Rút gọn A
419 40 19 419 40 19 . b) Giải phương trình 2
2x 2 3 3 x 3 3 0 . Trang 1
c) Biết nghiệm của phương trình 2
2x 2 3 3 x 3 3 0 là nghiệm của phương trình 4 2
4x bx c 0 . Tìm các số b, c . Lời giải a) Rút gọn
A 419 40 19 419 40 19 2 2 400 2.20. 19 19 400 2.20. 19 19 20 19 20 19
20 19 20 19 20 19 20 19 40 . Vậy A 40 . b) Giải phương trình 2
2x 2 3 3 x 3 3 0 . 2 2 2 3 3 4.2.3 3 12 9 12 3 24 3 12 9 12 3 2 3 3 0
phương trình có hai nghiệm phân biệt.
2 3 3 2 3 3
2 3 3 2 3 3 3 x ; x 3 . 1 2.2 2 2 2.2 3
Vậy phương trình có tập nghiệm là S 3; . 2
c) Biết nghiệm của phương trình 2
2x 2 3 3 x 3 3 0 là nghiệm của phương trình 4 2
4x bx c 0 . Tìm các số b, c . 3 Xét phương trình 4 2
4x bx c 0 , có hai nghiệm là 3; nên ta có: 2 4
34 b 32 c 0 4.9 .3 b c 0 3
b c 36 4 2 81 9 3 3 4. . b c 0 9
b 4c 81 4 b c 0 16 4 2 2 c 27 9
b 3c 1 08 c 27 36 c . 9
b 4c 8 1 b b 2 1 3 Vậy b 2
1;c 27 là các giá trị cần tìm. Bài 2. (2,0 điểm)
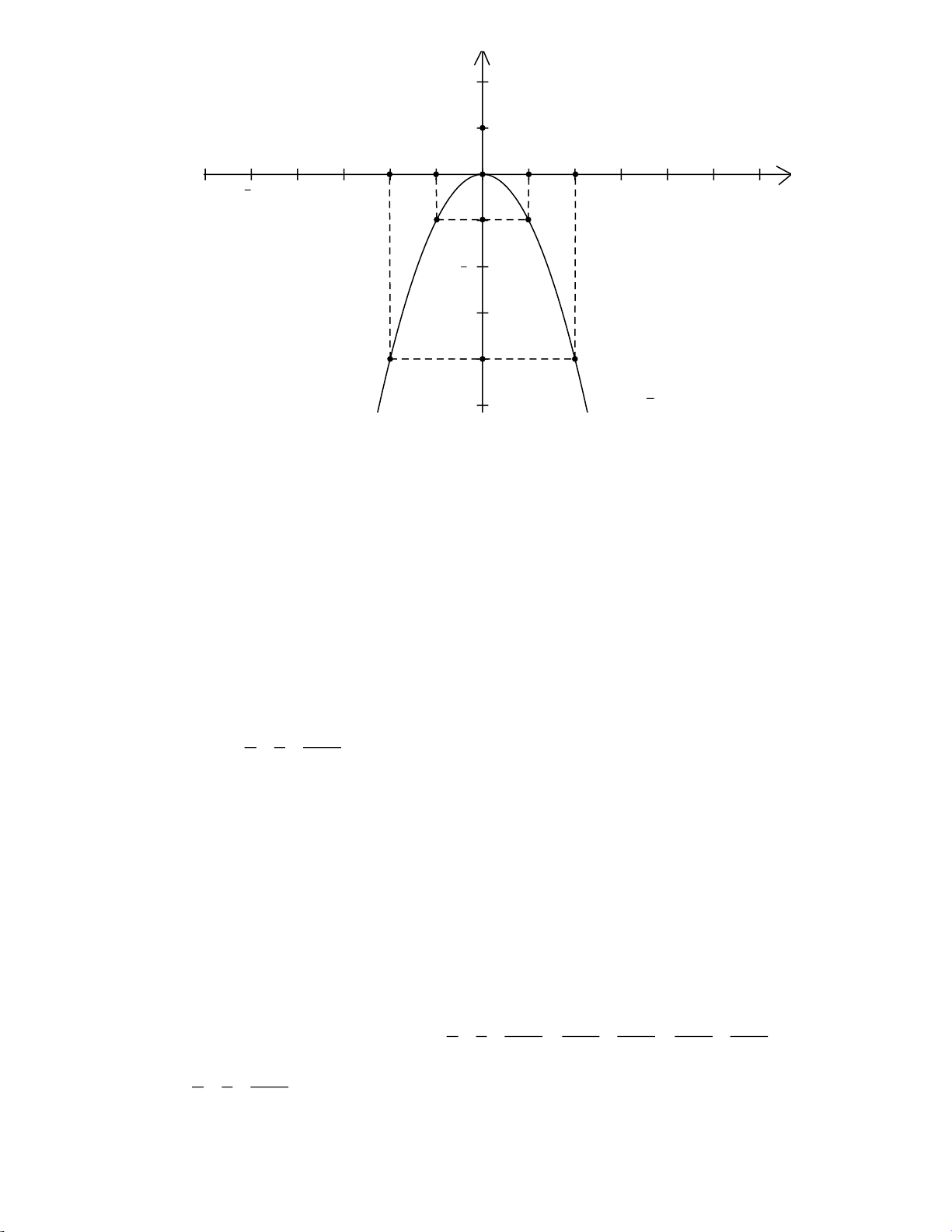
a) Vẽ đồ thị P của hàm số 2 y x .
b) Viết phương trình đường thẳng d đi qua điểm A0;
1 và tiếp xúc với P . Lời giải a) Vẽ đồ thị hàm số 2
y x P , ta có bảng sau: x -2 -1 0 1 2 2 y x -4 -1 0 -1 -1 Vậy đồ thị hàm số 2
y x P là Pa-ra-bol đi qua 2 ; 4 , 1 ; 1 , 0 : 0,1; 1 , 2; 4 và
nhận Oy làm trục đối xứng. Trang 2 y 2 1 x 5 -2 -1 O 1 2 5 -1 2 4 f x ( ) = x2
b) Viết phương trình đường thẳng d đi qua điểm A0;
1 và tiếp xúc với P .
Giả sử phương trình đường thẳng d có dạng y ax b .
d đi qua A0; 1 nên ta có 1 .
a 0 b b 1 d có dạng y ax 1.
Xét phương trình hoành độ giao điểm của d và P : 2 2
x ax 1 x ax 1 0 (1). Để d và
P tiếp xúc nhau thì (1) có nghiệm kép 2 2
0 a 4.1.1 0 a 4 a 2 .
Vậy ta có hai đường thẳng d thỏa mãn là y 2x 1 và y 2 x 1. Bài 3. (1,0 điểm)
Cho hai số a, b phân biệt thỏa mãn 2 2
a 2021a b 2021b c , với c là một số thực dương. 1 1 2021 Chứng minh rằng: 0 . a b c Lời giải Theo bài ra ta có 2 2
a 2021a b 2021b 2 2
a b 2021a 2021b 0
a ba b 202 1 0
a bktm .
a b 2021
Với a b loại do a, b phân biệt. Với 2 a b b a ab
a a 2 2021 2021 2021
a 2021a c . 1 1 2021 a b 2021 2021 2021
Thay a b 2021; ab c vào ta được 0 a b c ab c . c c 1 1 2021 Vậy 0 . a b c Bài 4. (2,0 điểm) Trang 3
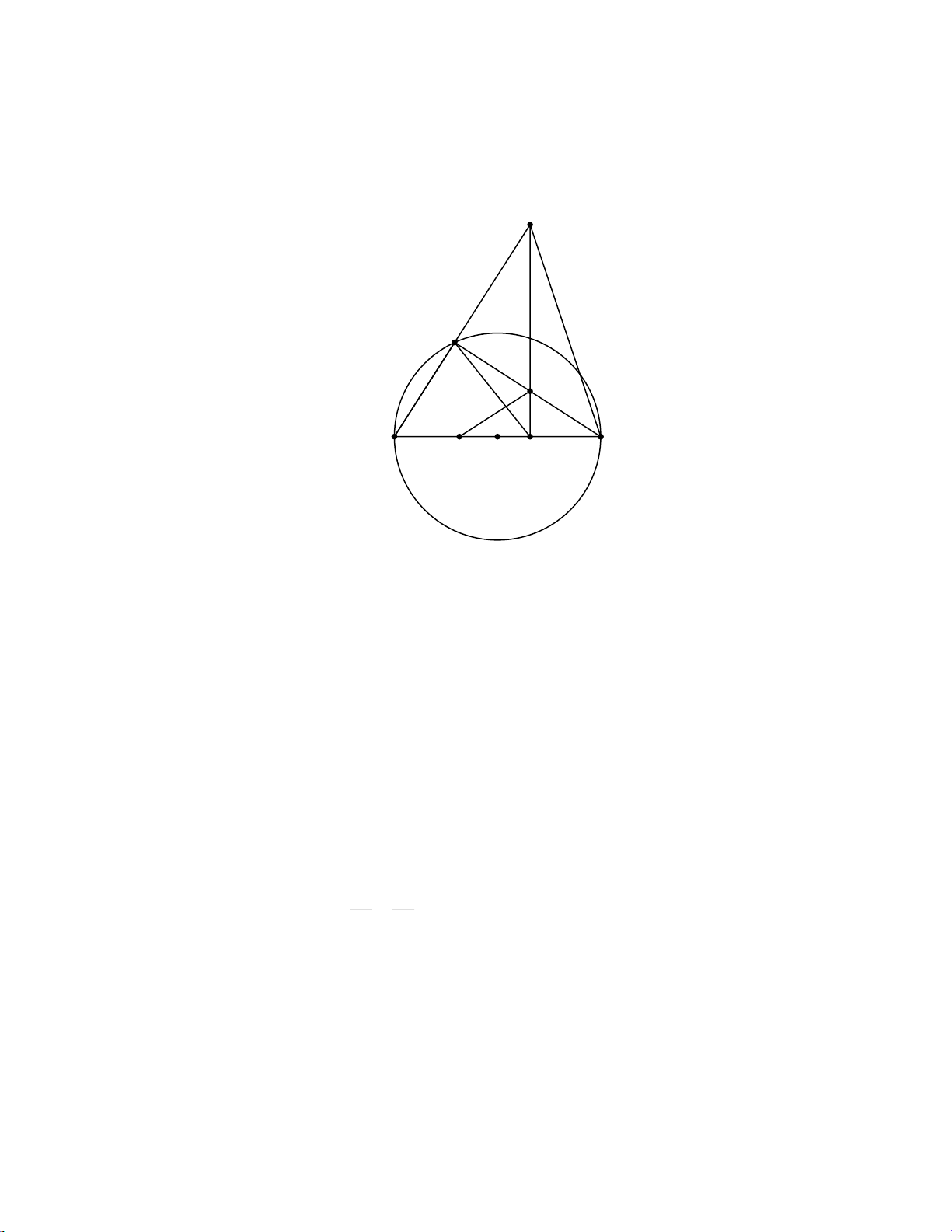
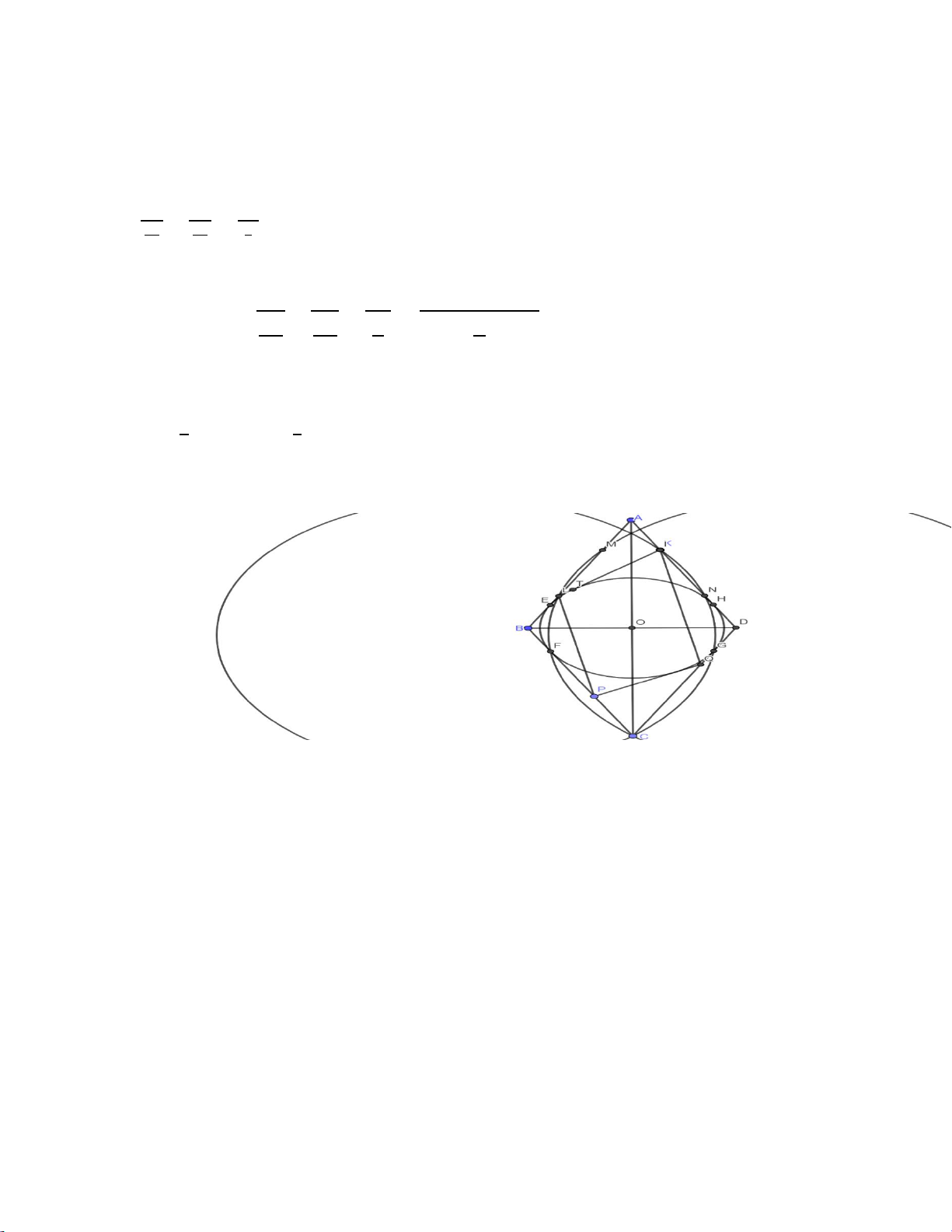
Cho tam giác ABC ( AB AC ) nội tiếp trong đường tròn O đường kính AC . Gọi I là một
điểm thuộc đoạn OC ( I khác O và C ). Qua I kẻ đường vuông góc với AC cắt BC tại E và AB
kéo dài tại D . Gọi K là điểm đối xứng của C qua điểm I .
a) Chứng minh rằng các tứ giác BDCI và AKED nội tiếp. b) Chứng minh I . C IA I . E ID . Lời giải D B E A K C O I
a) Chứng minh rằng các tứ giác BDCI và AKED nội tiếp.
Ta có ABC 90 (góc nội tiếp chắn nửa đường tròn) DBC 90 (kề bù với ABC 90 );
DIC 90 ( DI AC ) tứ giác BDCI nội tiếp đường tròn đường kính CD .
ECI EDB (hai góc nội tiếp cùng chắn BI ).
Lại có K là điểm đối xứng của C qua điểm I nên I là trung điểm của CK E KC có EI
vừa là trung tuyến, vừa là đường cao nên cân tại E EKI ECI EKI EDB ECI tứ giác
AKED có góc ngoài đỉnh K bằng góc trong đỉnh D nên là tứ giác nội tiếp.
b) Chứng minh I . C IA I . E ID . Xét I DA và I CE có:
IDA ICE (hai góc nội tiếp cùng chắn BI );
AID EIC 90 ,
DI AC ” ID IC IDA ICE g.g
IC.IA IE.ID . IA IE Bài 5. (1,0 điểm)
Cho tam giác ABC đều có diện tích 2
36 cm . Gọi M , N , P là ba điểm lần lượt nằm trên ba cạnh
AB, BC, CA sao cho MN BC; NP AC; PM AB . Chứng tỏ rằng tam giác MNP đều và tính
diện tích tam giác MNP . Lời giải Trang 4 C N P A B M Trong M
NB vuông tại M , ta có MBN MNB 90; mà PN BC GT
MNB MNP 90 MNP MBN 60 90 MNB; Trong A
MP vuông tại P , ta có AMP PAM 90 ; mà NM ABGT
AMP PMN 90 PMN PAM 60 90 AMP; M
NP có MNP PMN 60 nên là tam giác đều. 2 x 3
Đặt MN NP PN x vì M
NP đều nên S . MNP 4 Mặt khác B MN C NP A
PM (cạnh huyền – góc nhọn) S S S . BMN CNP APM x . 3 Trong tam giác
BMN vuông tạ M ta có BM MN. tan B . x cot 60 3 2 1 1 x 3 x 3 S BM .MN . .x . BMN 2 2 3 6 2 2 2 2 x 3 x 3 x 3 x 3 S 3.S S 36 3. 3 36 12 cm . ABC BMN MNP 2 6 4 4 4 Vậy 2 S 12 cm . MNP Bài 6. (1,0 điểm)
Hai ngọn nến hình trụ có chiều cao và đường kính khác nhau
được đặt thẳng đứng trên mặt bàn. Ngọn nến thứ nhất cháy hết trong 6
giờ, ngọn nến thứ hai cháy hết trong 8 giờ. Hai ngọn nến được thắp sáng
cùng lúc, sau 3 giờ chúng có cùng chiều cao.
a) Tìm tỉ lệ chiều cao lúc đầu của hai ngọn nến.
b) Biết tổng chiều cao của hai ngọn nến là 63 cm. Tính chiều cao của mỗi ngọn nến. Lời giải
a) Tìm tỉ lệ chiều cao lúc đầu của hai ngọn nến.
Gọi chiều cao ngọn nến thứ nhất là a cm, chiều cao ngọn nến thứ
hai là b cm, ( a, b 0 ).
Giả sử tốc độ tiêu hao khi cháy của hai ngọn nến là không đổi. 1 1
Mỗi giờ cây nến thứ nhất giảm
chiều cao, cây nến thứ hai giảm chiều cao. 6 8 Trang 5 1 1
Sau 3 giờ cây nến thứ nhất còn 1 3. chiều cao. 6 2 1
Chiều cao của cây nến thứ nhất còn lại là a . 2 1 5
Sau 3 giờ cây nến thứ hai còn 1 3. chiều cao. 8 8 5
Chiều cao của cây nến thứ hai còn lại là b . 8
Vì sau 3 giờ chiều cao của hai cây nến bằng nhau nên 1 5 a 5 a b . 2 8 b 4 5
Vậy tỉ lệ chiều cao ban đầu của ngọn nến thứ nhất so với ngọn nến thứ hai là . 4
b) Biết tổng chiều cao của hai ngọn nến là 63 cm. Tính chiều cao của mỗi ngọn nến.
Tổng chiều cao ngọn nến là 63 cm a b 63.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: a 5 a b a b 63 7 . b 4 5 4 5 4 9 a b Vì
7 a 7.5 35cm; 7 b 7.4 28cm . 5 4
Vậy ban đầu ngọn nến thứ nhất cao 35 cm, ngọn nến thứ hao cao 28 cm.
= = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =
TUYỂN SINH LỚP 10 THPT CHUYEN LÊ QUÝ ĐÔN TỈNH BÀ RỊA VŨNG TÀU
ĐỀ THI MÔN : TOÁN (Chuyên) Năm học: 2021-2022 Câu 1 (3, 0 điếm). x x 1 x 1 x 2
a) Rút gon biểu thức P
với x 0, x 1, x 4 . 1 x x x 1 x x 2
b) Giadi phương trình 5x (x 4) 2x 1 4 0. 2 2
2x y 3xy 4x 3y 2 0
c) Giai hế phương trinh . 2
x y 3 x y 1 2 Câu 2 (2, 0 điểm). a) Cho hai da thức 3 2
P(x) x ax bx c và 2
Q(x) 3x 2ax b(a, ,
b c ) . Biết rằng
P(x) có ba nghiệm phân biệt. Chưng minh Q(x) có hai nghiềm phân biệt.
b) Tìm tất cả các cặp số nguyên (x; y) thơa mần phương trình 2 2 2
(xy 1) x y .
Câu 3 (1, 0 điểm). Xét các số thực a,b, c không âm, thòa măn 2 2 2
a b c 1. Tìm giá trị a b c
lớn nhất và giá trị nhỏ nhất của biểu thức S . 1 bc 1 ac 1 ab Trang 6
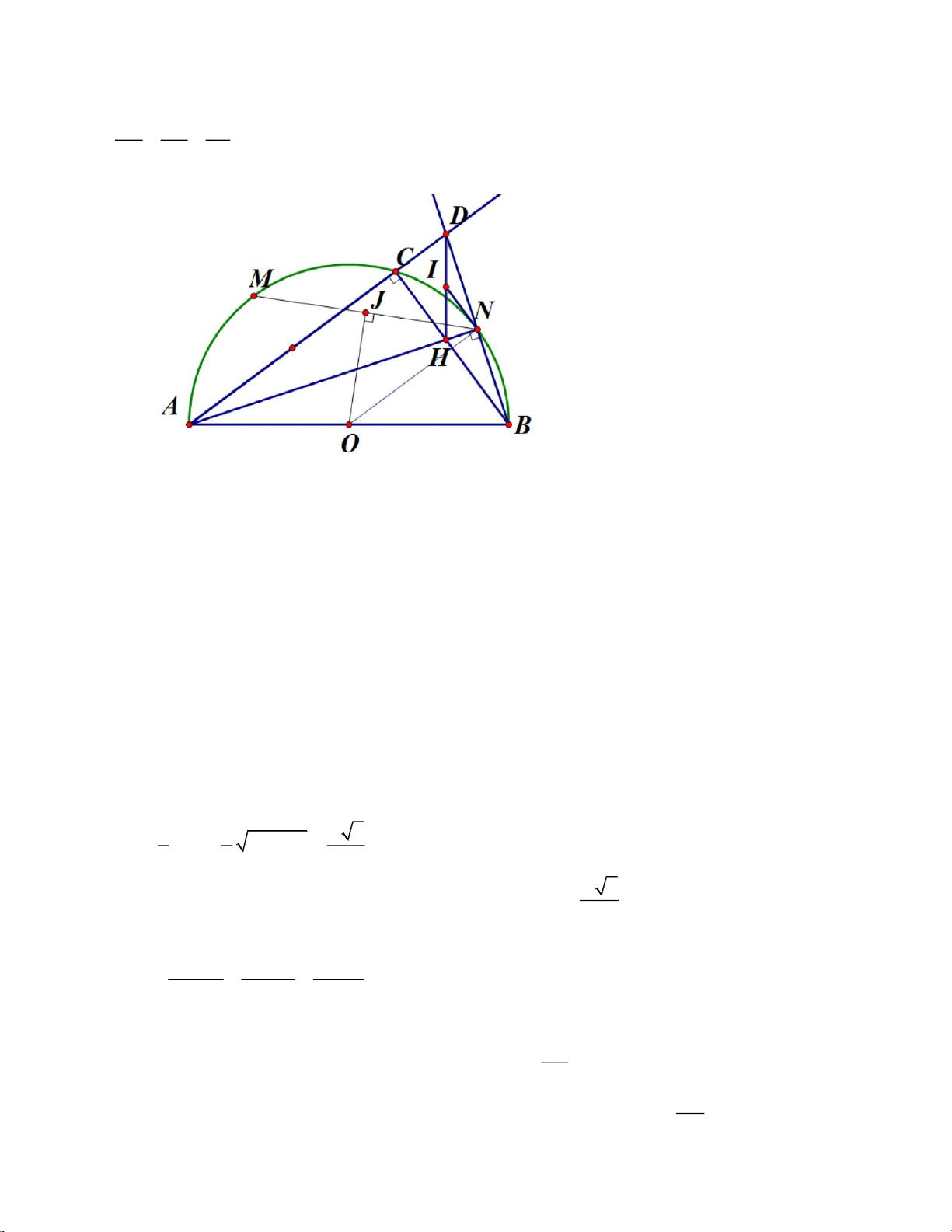
Câu 4 (3, 0 điểm). Cho tam giác ABC nhọn ( AB AC ). Một đường trơn đi qua B,C và
khỏng đi qua A cat các cạnh AB, AC lần lượt tại E, F (E khác B; F khác C ); BF cảt
CE tại D . Gọi P là trung điểm của BC và K là điềm đối xứng với D qua P . AE DE
a) Chứng minh tam giác KBC đồng dạng với tam giác DFE và . AC CK
b) Gọi M , N lần lượt là hình chiếu vuông góc của D trên AB, AC . Chửng minh MN
vuông góc với AK và 2 2 2 2
MA NK NA MK .
c) Gọi I , J lần lựt là trung điềm AD và MN , Chứng minh ba điếm I , J , P thẳng hàng.
d) Đường thẳng IJ cát đường tròn ngoại tiếp tam giác IMN tại T ( T khade l ). Chưng
minh AD là tićp tuyến của đường tròn ngoại tiếp tam giác DTJ .
Câu 5: (1 điểm) Cho tam giác ABC và điểm O thay đổi trong tam giác.Tia Ox song song với AB
cắt BC tại D , tia Oy song song vói BC cắt AC tai E , tia Oz song song vói AC cắt AB 2 2 2 AB BC AC
tạ F . Tìm giá trị nhỏ nhất của biểu thức S OD OE OF HƯỚNG DẪN Câu 1 (3.0 điêm). x x 1 x 1 x 2
a) Rút gọn biểu thức sau P với 1 x x x 1 x x 2
x 0, x 1, x 4
b) Giải phương trình 5x (x 4) 2x 1 4 0 . 2 2
2x y 3xy 4x 3y 2 0
c) Giải hệ phương trình . 2
x y 3 x y 1 2 3 ( x ) 1 x 1 x 2 P 1 x x
( x 1)( x 1)
( x 1)( x 2) 1 1 ( x 1) x 1 x 1 2 ( x 1)
( x 1)( x 1) 2 x 1 Điề 1 u kiện: x
. Đặi t 2x 1(t 0) . Ta có phương trình 3 2 t
5t 7t 3 0 2 t (t 1) 1 2 t
4t 3 0 (nhận). t 3
* Vơi t 1 2x 1 1 x 0 (thỏa).
* Với t 3 2x 1 3 x 4 (thỏa). Trang 7 2 2
2x y 3xy 4x 3y 2 0 (1)
2x y3 x y12 (2) 2 Điề x y 3 0 ù kiện:
x y 1 0 (1): 2 2
y (3x 3) y 2x 4x 2 0 y 2x 2
(x 1) nên (1) y y x
* TH1: y x 1 thay vào (2) ta có phương trình
x 0 y 1 2
x x 4 2 (nhận)
x 1 y 0 * TH2: y 2
x 2 thay vào (2) ta có phương trình 2 2
x 2x 5 x 1 2 (x 1) 4 ( x 1) 2 Ta có 2 (x 1) 4 (
x 1) 2 , với mọi giá trị của x 1 Dấu bằng xảy ra khi x 1
y 0 (nhận) Vậy hệ phương trình có các nghiệm là (0; 1 ),( 1 ;0) . Câu 2 (2, 0 điểm). a) Cho hai đa thức 3 2
P(x) x ax bx c và 2
Q(x) 3x 2ax b(a, ,
b c ) . Biết rằng
P(x) có ba nghiệm phân biệt. Chứng minh Q(x) có hai nghiệm phân biệt.
b) Tìm tất cả các cặp số nguyên (x; y) ihỏa mãn phương trình 2 2 2
(xy 1) x y
a) Gọi x , x , x là ba nghiệm phân biệt của P(x) , ta có P(x) x x x x x x 1 2 3 1 2 3 3
x x x x 2
x x x x x x x x x x x 1 2 3 1 2 1 3 2 3 1 2 3
Đồng nhất hệ số của P(x) ta có: 2
a 3b (x x x )2 (
3 x x x x x x ) Q 1 2 3 1 2 1 3 2 3 1
(x x )2 (x x )2 (x x )2 1 2 2 1 3 0 2 3
Vậy Q(x có hai nghiệm phân biệt
Lưu y: hs sử dụng Viet vẫn cho điểm tối đa b/ 2 2 2 2 2
xy xy x y x y xy Ta có: (xy-1)2=x2+y2 ( ) 2 1 ( ) ( ) 1
x y xy 1 ) 1 (
x y xy 1
(x y xy)(x y xy) 1
x y xy 1 ( ) 2
x y xy 1
Giải hệ (1) ta được cặp nghiệm (0;1),(1;0)
Giải hệ (2) ta được cặp nghiệm (0;-1),(-1;0) Câu 3: Trang 8 1 ( )2 bc 1 2 2 2 2 2 2
bc b c a b c 2bc 2 2 2 b c 2 2 2 2 2 2 1
a (b c) b c a (b c) (a b c)2 2 1 a c
Ta có : 1 bc
(a b c) 2 ...tuongtu 2 1 bc
a b c S a b c 2( ) 2
a b c
a b c
a b c 2 Khi a=b=
, c 0 thì S = 2 . Vậy giá trị lớn nhất của S là 2 . 2 Theo BĐT AM-GM: 2 2 2 2 2 2 2 2 2 a 1 b c (a 2 )( 1
b c ) 1 a 1 2 b c 2 a 1 ( ) bc 1 ( ) ( ) 2 2 4 4 2 Từ đó : a b c 2 2 2 2 2 2 a . Tuong tu b ;
c S a b c 1 Khi a 1;b c 0 thì S 1 . 1 bc 1 ac 1 ab
Vậy giá trị nhỏ nhất của S là 1. Câu 4:(3 điểm) Chưa vẽ hình
Tứ giác BCFE nội tiếp nên ta có: DEF DBC ; DFE DCB
Mặt khác: BDCK là hình bình hành nên BCK DBC ; CBK DCB DFE C K B K BC D FE(gg)
Do đó : DEF BCK ; DE EF FE AE K BC D FE (1); A EF A CB (2) CK BC BC AC AE DE Từ (1) và (2) AC CK
Gọi Q là giao điểm của MN và AK . Ta có: AEC ABK (đồng vi) và
ABK ABD DBK ACE DCK ACK
(Do ABD ACE; DBK DCK) DE AE Xét AED và A
CK có: AED ACK, AE D ACK
(c g c) CK AC
KAC DAE hay QAC DAM
b) Có AMD AND 180 AMDN nội tiếp DNM DAM QAN .
Mà DNM MNA 90 QAN MNA 90 AQN 90 AK MN Do đó: 2 2 2 2 2 2
MA NK QM QA QN QK 2 2 2 2 2 2
QN QA QM QK NA MK Trang 9 1 Ta có MI
AD NI I thuộc đường trung trực của MN (3) 2
c) Ta có IP là đường trung bình của tam giác ADK IP / / AK IP MN (4)
Từ (3) và (4) suy ra IP là đường trung trực của MN I , J , P thẳng hàng. Từ (3) và Ta có I
MN cân tại I, IJ MN nên IT là đường kính của đường tròn ngoại tiếp 2 I
MN INT 90 IJ.IT IN Mà 2
IN ID IJ.IT ID I DJ I
TD( g g) IDJ ITD
ID là tiếp tuyến của đường tròn ngoại tiếp D TJ .
Câu 5(1, 0 điểm). Cho tam giác ABC và điểm O thay đổi trong tam giác. Tia Ox song
song với AB cắt BC tại D , tia Oy song song với BC cắt AC tại E , tia Oz song song 2 2 2 AB BC AC
với AC cắt AB tại F . Tìm giá trị nhỏ nhất của biểu thức S OD OE OF
Kẻ DM / / OF (M AB), EN / /OD(N BC), FP / /OE(P AC) OD EN NC OE DN OF MD BD Ta có: (1); (2); (3) AB AB BC BC BC AC AC BC OD OE OF NC DN BD Từ (1), (2), (3) 1 AB BC AC BC BC BC
Theo bất đẳng thức AM-GM: OD OE OF OD OE OF AB BC AC 3 1 3 27 AB BC AC AB BC AC OD OE OF 2 2 2 2 AB BC AC AB BC AC 3 S 3 27 OD OE OF OD OE OF
Đẳng thức xảy ra khi O là trọng tâm ABC
. Vậy giá trị nhỏ nhất của S là 27 .
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 BẾN TRE
TRUNG HỌC PHỔ THÔNG CÔNG LẬP
NĂM HỌC 2021 – 2022 ĐỀ CHÍNH THỨC Môn: TOÁN (chuyên)
Thời gian: 150 phút (không kể phát đề) Câu 1. (2,0 điểm)
y 6 7m a)
Tìm tất cả các giá trị của tham số m để hàm số
x 2 nghịch biến trên .
b) Cho Parabol P 2
: y 2x và đường thẳng d : y x 6 . Biết d cắt P tại hai
điểm phân biệt A x ; y , B x ; y với x x . Tính 4x y . 2 2 1 1 1 2 2 1
A x 2 2 c) Rút gọn biểu thức 1
4x 4 x 2 7 (với x 2). Câu 2. (1,0 điểm) Cho phương trình: 2
x m 3 x 4m 4 0 (1), với m là tham số. Tìm m để phương trình (1)
có hai nghiệm phân biệt x ; x thỏa x
x x x 20 . 1 2 1 2 1 2 Câu 3. (3,0 điểm) 2 2 2 a)
Giải phương trình nghiệm nguyên: x y xy 2x 1 y xy 2y . Trang 10 2
y 2xy 2 0
b) Giải hệ phương trình: 2 2
4x y y 2x 2 0. c)
Giải phương trình: x x x 2 3 2 5 2
2 2x 9x 10 1. Câu 4. (1,0 điểm)
Cho ba số thực dương x , y z thỏa 3 xy
xz 2 . Chứng minh rằng: 4 yz 5xz 7xy 8 . x y z Câu 5. (2,0 điểm)
Cho tam giác ABC vuông tại A với ( AB AC ), có đường cao AH . Biết BC 1dm và 12 AH dm . 25
a) Tính độ dài hai cạnh AB và AC
b) Kẻ HD AB ; HE AC (với D AB , E AC ). Gọi I là trung điểm của BC . Chứng
minh IA DE . Câu 6. (1,0 điểm)
Cho tam giác ABC có đường phân giác ngoài của góc A cắt đường thẳng BC tại điểm D . Gọi
M là trung điểm của BC . Đường tròn ngoại tiếp A
DM cắt các đường thẳng AB , AC lần lượt tại
E và F (với E , F khác A ). Gọi N là trung điểm của EF . Chứng minh rằng MN // AD .
LỜI GIẢI CHI TIẾT Câu 1. (2,0 điểm)
y 6 7m a)
Tìm tất cả các giá trị của tham số m để hàm số
x 2 nghịch biến trên .
b) Cho Parabol P 2
: y 2x và đường thẳng d : y x 6 . Biết d cắt P tại hai
điểm phân biệt A x ; y , B x ; y với x x . Tính 4x y . 2 2 1 1 1 2 2 1
A x 2 2 c) Rút gọn biểu thức 1
4x 4 x 2 7 (với x 2). Lời giải 6
y 6 7m a) Hàm số
x 2 nghịch biến trên
6 7m 0 m . 7 6 Vậy m
thì hàm số đã cho nghịch biến trên . 7
b) Xét phương trình hoành độ giao điểm của P và d , ta có: 2 2
2x x 6 2x x 6 0 Có: 2 1 4.2.6 49 0
Vậy phương trình có 2 nghiệm phân biệt: 1 49 1 49 3 x 2 và x 1 2.2 2 2.2 2 Với x 2
, ta có y 8, suy ra A 2 ;8. 1 1 3 9 3 9 Với x , ta có y , suy ra B ; 2 2 2 2 2 2 . Khi đó, ta có: Trang 11 3
4x y 4. 8 14 . 2 1 2
Vậy 4x y 4 1 . 2 1 c)
A x 2 2
1 4x 4 x 2 7
x 2 2 x 2 1 2 x 22 2.2 x 2 1
x 1 2 x 2 2 x 2 2 1
x 1 2 x 2 2 x 2 1
x 1 2 x 2 2 x 2 1
do 2 x 2 1 0 x Vậy A x . Câu 2. (1,0 điểm) Cho phương trình: 2
x m 3 x 4m 4 0 (1), với m là tham số. Tìm m để phương trình (1)
có hai nghiệm phân biệt x ; x thỏa x
x x x 20 . 1 2 1 2 1 2 Lời giải 2 2 2 2
Ta có: m 3 44m 4 m 6m 9 16m 16 m 10m 25 m 5
Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi
m 2 0 5
0 m 5 0 m 5
Vậy với m 5 thì phương trình (1) có hai nghiệm phân biệt. x 0 Theo đề 1 bài ta có:
x x x x 20 (2), với điều kiện 1 2 1 2 x 0 2
Do đó, phương trình (1) có hai nghiệm phân biệt thỏa mãn x 0 và x 0 , nghĩa là 1 2 m 5 m 5 m 5
m 3 0 m 3 (*) m 1 4m 4 0 m 1
x x m 3 1 2
Áp dụng định lý Vi-et, ta có: x x 4m 4 1 2 Ta có:
x x 2 x x 2 x x 1 2 1 2 1 2
m 3 2 4m 4
m 3 4 m 1
m 1 4 m 1 4 m 1 22 Từ đó, ta suy ra
x x m 1 2
do m1 2 0, m 1 1 2
Từ phương trình (2), ta được Trang 12
x x x x 20 m 1 2 4m 4 0
2 m 1 22 4m (3) 1 2 1 2 11
Giải phương trình (3) với điều kiện: 22 4m 0 m (**) 2
3 m 1 22 4m2 2
m 1 484 176m 16m 2
16m 177m 485 0 4 Ta có: 177
2 4.16.485 289 0
Vậy phương trình (4) có 2 nghiệm phân biệt: 177 289 177 289 97 m 5 và m 2.16 2.16 16
So với điều kiện (*) và (**) thì m.
Vậy không tồn tại giá trị của m thỏa mãn yêu cầu bài toán. Câu 3. (3,0 điểm) 2 2 2 a)
Giải phương trình nghiệm nguyên: x y xy 2x 1 y xy 2y . 2
y 2xy 2 0
b) Giải hệ phương trình: 2 2
4x y y 2x 2 0. c)
Giải phương trình: x x x 2 3 2 5 2
2 2x 9x 10 1. Lời giải a) Ta có: 2 2 2
x y xy 2x 1 y xy 2 y 2 2 2
x y xy 2x 1 y xy 2y 0 2 2
x y xy 2
xy y 2 x y 1
xy x y y x y 2x y 1
x yxy y 2 1 1
Vì đây là phương trình nghiệm nguyên nên ta có:
x y 1 (*) xy y 2 1 1 x y 1 **
xy y 2 1 x 1 y x 1 y x 1 y
x 0; y 1 * y 1 y 1 2
y y 1 0 y 1 0
x 2; y 1 y 1 x 1 y x 1 y x 1 y x 2 ; y 1 ( * * ) y 1 y 1 2
y y 3 0
y 2y 3 0
x 2; y 3 y 3 Trang 13
Vậy tập nghiệm của hệ phương trình là: S
0; 1,2; 1, 2 ; 1 ,2; 3 . b) Ta có: 2 2
y 2xy 2 0
y 2xy 2 2 2
4x y y 2x 2 0 2 2 4x y
y 2x 2y 2xy 0 2
y 2xy 2
2x y
2x y 2x y y2x y 0 2
y 2xy 2 2x y
2x y 1 y 0 2
y 2xy 2
2x y 2x 1 0 2
y 2xy 2
2x y 0 2x 1 0 2
Mặt khác, y 2xy 2 y y 2x 2 , nghĩa là y 2x 0 .
Do đó, từ hệ phương trình ban đầu đề cho, ta giải hệ phương trình sau: 1 1 x 2
y 2xy 2 x 2 2 y 1 2x 1 0 2
y y 2 0 y 2 1 1
Vậy hệ có tập nghiệm là S ; 1 , ;2 2 2 c)
Giải phương trình (*): x x x 2 3 2 5 2
2 2x 9x 10 1. 5 x 2x 5 0 2
Điều kiện xác định: x 2 0 x 2 x 2 . 2
2x 9x 10 0 5 x x 2 2
a 2x 5 a 1 Ta đặt b x 2 b 0 2 2
a 2b 2x 5 2x 2 1 Ta thấy 2 2
a b 2x 5 x 2 x 3
ab 2x 5 x 2 2
2x 9x 10
Phương trình (*) trở thành: Trang 14 2 2
a b a 2b 2 2
ab a 2b 2 2
a b a 2b 2 2
a b 2
b ab 0 2 2
a b a 2b 1 2
b ab 0
a ba ba 2b
1 b a b 0
a ba ba 2b 1 b 0 a b 0 1
aba2b 1b 0 2
Vì a b 1 nên ta chỉ giải phương trình (2)
a ba 2b
1 b 0 a ba b
1 b a b b 0
a ba b
1 b a b 1 0
a b a b a b 1 0 1 2
0 a2b 0
TH1: Với a 2b 0 , ta có
a 2b 0 2x 5 2 x 2 0
2x 5 2 x 2
x x 3 2 5 4 2 x 2 3
So với điều kiện thì x (Nhận). 2
TH2: Với a b 1 0 , ta có
a b 1 0 2x 5 x 2 1 0
2x 5 x 2 1
2x 5 x 3 2 x 2
x 2 2 x 2 0
x 2 x 2 2 0 x 2 0 x 2 0 x 2 x 2
x 2 2 0 x 2 2 x 2 4 x 2
So với điều kiện thì x 2 (Nhận) và x 2 (Nhận). 3
Vậy tập nghiệm của phương trình là S 2; ; 2 . 2 Câu 4. (1,0 điểm)
Cho ba số thực dương x , y z thỏa 3 xy
xz 2 . Chứng minh rằng: 4 yz 5xz 7xy 8 . x y z Lời giải 4 yz 5xz 7xy Ta đặt M , ta có x y z Trang 15 4 yz 5xz 7xy M x y z yz yz xz xz xy xy 3 4 3 4 x x y y z z yz xz yz xy xz xy 3 4 x y x z y z
Áp dụng bất đẳng thức Cauchy, ta được yz xz yz xy xz xy M 2 . 3.2 . 4.2 . x y x z y z
2z 6y 8x
2z 2x 6y 6x
Tiếp tục áp dụng bất đẳng thức Cauchy, ta được
M 2.2 xz 6.2 xy
4 xz 3 xy 4.2 8
x y z 1
Dấu “ ” xảy ra khi và chỉ khi
x y z .
xz 3 xy 2 2 1
Vậy khi x y z thì M 8 (đpcm). 2 Câu 5. (2,0 điểm)
Cho tam giác ABC vuông tại A với ( AB AC ), có đường cao AH . Biết BC 1dm và 12 AH dm . 25
a) Tính độ dài hai cạnh AB và AC
b) Kẻ HD AB ; HE AC (với D AB , E AC ). Gọi I là trung điểm của BC . Chứng
minh IA DE . Lời giải
a) Tính độ dài hai cạnh AB và AC
Áp dụng hệ thức lượng và định lý Pytago cho ABC
vuông tại A , ta có: Trang 16 2 2 2 2 2
AB AC BC 1
AB AC 1 12 144 2 2 A .
B AC AH.BC AB .AC 25 625 Khi đó, 2 AB 2
và AC là các nghiệm dương của phương trình.
Áp dụng hệ quả của định lý Vi-et, ta được 144 2 X 1X 0 625 144 49 2 Ta có: 1 4.1.
0 nên phương trình trên có 2 nghiệm phân biệt: 625 625 49 49 1 1 625 9 625 16 X và X 1 2.1 25 2 2 25
Theo giả thiết, AB AC , nên ta được: 16 4 2 AB X AB 1 2 2 25 5
AB AC 9 3 2 AC X AC 2 25 5 4 3 Vậy AB dm và AC dm . 5 5
b) Chứng minh IA DE .
Gọi F là giao điểm của AI và DE . HEA 90 HE AC
Xét tứ giác EHDA , ta có: HDA 90 HD AB DAE 90 ABC vuoâ ng taïi A
Tứ giác EHDA là hình chữ nhật (tứ giác có 3 góc vuông)
Tứ giác EHDA là tứ giác nội tiếp.
ADE AHE (hai góc nội tiếp cùng chắn cung AE )
Mà AHE ECH (cùng phụ với CHE )
ADE ECH ADE ACB (1) Xét ABC
vuông tại A có I là trung điểm của BC 1
IA IB BC (định lý đường trung tuyến trong tam giác vuông) 2 I
AB cân tại I IAB IBA (2)
Từ (1) và (2), ta suy ra: ADE IAB ACB IBA ACB ABC 90 ( ABC vuông tại A )
Áp dụng định lý tổng 3 góc trong A DF , ta có: Trang 17
FAD FDA AFD 180 AFD 180 FAD FDA
AFD 180 IAB ACB
AFD 180 ABC ACB
AFD 180 90 90 ABC vuoâng taïi A
Do đó, IA DE (đpcm) Câu 6. (1,0 điểm)
Cho tam giác ABC có đường phân giác ngoài của góc A cắt đường thẳng BC tại điểm D . Gọi
M là trung điểm của BC . Đường tròn ngoại tiếp A
DM cắt các đường thẳng AB , AC lần lượt tại
E và F (với E , F khác A ). Gọi N là trung điểm của EF . Chứng minh rằng MN // AD . Lời giải
Dựng hình bình hành BPCF .
Hai đường chéo BC và PF cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC (gt) M cũng là trung điểm của PF . Xét PEF
, ta có N là trung điểm của EF (gt), M là trung điểm của PF (cmt)
MN là đường trung bình của PEF MN EP (1)
Ta có: MPB MFA (cặp góc so le trong của PB
FA , PBFC là hình bình hành)
Mà MDA MEA MFA (các góc nội tiếp cùng chắn cung AM )
MEA MPB , nghĩa là MEB MPB
Xét tứ giác BMEP , ta có MEB MPB (cmt)
Tứ giác BMEP nội tiếp (tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau)
BEP BMP (hai góc nội tiếp cùng chắn cung BP )
Mà BMP FMD (đối đỉnh)
Mặt khác FMD FAD (hai góc nội tiếp cùng chắn cung FD )
BEP FAD , nghĩa là AEP FAD (2)
Ta có: AD là phân giác ngoài của BAC (gt) Trang 18
Mà BAC CAE 180 (kề bù)
AD là phân giác của CAE FAD EAD (3)
Từ (2) và (3), ta suy ra AEP EAD
Mà 2 góc nằm ở vị trí so le trong nên EP AD (4)
Từ (1) và (4), ta suy ra MN AD (đpcm)
SỞ GIÁO DỤC – ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2021- 2022 BÌNH ĐỊNH
Đề chính thức Môn thi: Toán
Ngày thi: 11/6/2021 Thời gian làm bài: 120’
Bài 1: (2 điểm). x 1 1 2 1.Cho biểu thức P :
Với x>0;x 1 x 1 x 1 x 1 x 1
a) Rút gọn biểu thức P
b) Tìm giá trị của P khi x 4 2 3
x 2y 6
2. Giải hệ phương trình:
2x 3y 7 Bài 2: (2 điểm)
1. Cho phương trình x2-(m+3)x-2m2+3m=0 (m là tham số). Hãy tìm giá trị của m để x=3 là nghiệm của
PT và xác định nghiệm còn lại của PT ( nếu có)
2. Cho Parabol (P): y=x2 và đường thẳng (d) : y= (2m+1)x-2m (m là tham số). Tìm m để đường thẳng (d)
cắt (P) tại hai điểm phân biệt A x , y ; B x , y sao cho: y 2 2 1 1 1+y2 - x1 x2=1
Bài 3: (2,0 điểm)
Một xe máy khởi hành tại địa điểm A đi đến địa điểm B cách A 160 km, sau đó 1 giờ, một ô tô đi từ
B đên A. Hai xe gặp nhau tại địa điểm C cách B 72 km. Biết vận tốc ô tô lớn hơn vận tốc xe máy 20km/h. Tính vận tốc mỗi xe.
Bài 4: (4,0 điểm) 0
Cho tam giác ABC có ACB 90 nội tiếp trong đường tròn tâm O. Gọi M là trung điểm của BC,
đường thảng OM cắt cung nhỏ BC tại D, cắt cung lớn BC tại E. Gọi F là chân đường vuông góc hạ từ E
xuống AB; H là chân đường vuông góc hạ từ B xuống AE
a) Chứng minh tứ giác BEHF nội tiếp.
b) Chứng minh MF AE
c) Đường thẳng MF cắt AC tại Q. Đường thẳng EC cắt AD, AB lần lượt tại I và K. Chứng minh EC EK 0 EQA 90 & IC IK
Bài 5 (1,0 điểm). 1 1 1 1
Cho a,b, c là các số dương thỏa:
2.CMR : abc 1 a 1 b 1 . c 8
HƯỚNG DẪN GIẢI Bài 1: 1.
a) Rút gọn biểu thức P : ĐK: x 0; x 1 Trang 19 x 1 1 2 x x x 1 x 1 2 x 1 x 1 x 1 P : x 1 x 1 x 1
x 1 x : 1 x 1 x . x 1 1 x 1 x 1 x 1 x 1 Vậy P
với x 0; x 1 x 1
b) Tìm giá trị của P khi x 4 2 3 :
với x 0; x 1, ta có: x 2 4 2 3 3 1 3 1 3 1 x 1 4 2 3 1 5 2 3 5 3 6 P x 1 3 11 3 3 Vậy ……….
x 2y 6 x 4 2. ....
Vậy HPT có nghiệm duy nhất
2x 3y 7 y 5
Bài 2: (2điểm)
1. Cho phương trình x2-(m+3)x-2m2+3m=0 (m là tham số). Hãy tìm giá trị của m để x=3 là nghiệm của
PT và xác định nghiệm còn lại của PT ( nếu có). 2 2 2
Vì x=3 là nghiệm của PT, nên: 3 m 3.3 2m 3m 0 2m 0 m 0 b
Khi đó theo hệ thức Vi-et, ta có: x x
m 3 0 3 3 x 3 x 3 3 0 1 2 2 1 a Vậy……….
2. Cho Parabol (P): y=x2 và đường thẳng (d) : y= (2m+1)x-2m (m là tham số). Tìm m để đường thẳng (d)
cắt (P) tại hai điểm phân biệt A x , y ; B x , y sao cho: y 2 2 1 1 1+y2 - x1 x2=1:
Hoành độ giao điểm của (d) và (P) là nghiệm của pt:
x2=(2m+1)x-2m x2- (2m+1)x+2m=0 (1)
2m 2 1
m m m m m m m 2 2 2 4.1.2 1 4 4 8 4 4 1 2 1 0
(d) cắt (P) tại hai điểm phân biệt A x , y ; B x , y
PT (1) có 2 nghiệm phân biệt x 2 2 1 1 1 x2
m 2 1 0 2 1
0 2m 1 0 m 2 b x x 2m 1 1 2 a
Theo hệ thức Vi- ét, ta có: mà y= x2, nên: c
x .x 2m 1 2 a 2 2 2 2
y y x x 1 x x x x 1 x x
3x x 1 2m 1 3.2m 1 1 2 1 2 1 2 1 2 1 2 1 2
m 0 TM 2
4m 2m 0 2m(2m 1) 0 1
m KTM 2
Vậy m=0 thỏa mãn yêu cầu .
Bài 3: (2,0 điểm) 160 km Trang 20 A B C 72 km
Gọi vận tốc của xe máy là x (km/h) ĐK: x > 0
Vận tốc của ô tô là : x+20 (km/h)
Quãng đường AC: 160-72=88 (km) 88
Thời gian xe máy đi từ A đến C là: (giờ) x 72
Thời gian ô tô đi từ B đến C là: x (giờ) 20
Vì ô tô khởi hành sau xe máy 1 giờ nên ta có pt: 88 72 x 40(TM ) 2 1
1 x 4x 1760 0 ... x x 20 x 4 4(KTM ) 2
Vậy vận tốc của xe máy là 40 (km/h)
Vận tốc của ô tô là : 40+20 = 60(km/h)
Bài 4: (4,0 điểm)
a) Chứng minh tứ giác BEHF nội tiếp: 0 0
Ta có: BFE 90 Vì F
E AB; BHE 0 9
Vì BH BC => Tứ giác BKMI nội tiếp (Tứ giác
có hai đỉnh kề H,F cùng nhìn BE dưới góc bằng nhau) C D
b)Chứng minh MF AE : M Ta có: MB=MC (gt) => 0
EM BC BME BFE BHE 90
3 điểm M;F;H cùng nằm trên đường tròn đường kính BE F 1
=>5 điểm B;M;F;H;E cùng nằm trên đường tròn đường kính BE A B 2
=> F E ( góc nội tiếp cùng chắn cung MB) (1) 1 1 O
Và B E ( góc nội tiếp cùng chắn cung FH) (2) 2 2
Lại có: EM BC Cung BE= cung CAE H 2 1
MBE FAE ( Góc nội tiếp chắn hai cung băng nhau) 0 0
Mà MBE E 90 ; FAE E 90 ( tam giác vuông) 1 2 E
Suy ra: E E (3) 1 2
Từ (1); (2) và (3) Suy ra: B F , mà hai góc này ở vị trí so le trong, nên: MF//BH ,mà BH AE 2 1 MF AE C EC EK 0 D
c) Chứng minh EQA 90 & IC IK M
Ta có: ED BC Cung DB= cung DC=> A A 1 2 1 I 2 F 1 A B
=> AI là đường phân giác trong của tam giác AKC 2 K 0
Mà DAE 90 ( Góc nội tiếp chắn nửa đtròn) AI AE Q O
=> AE là đường phân giác ngoài của tam giác AKC
Theo tính chất đường phân giác của tam giác ta có: H IC AC EC AC IC EC EC EK 2 & hay (đ.p.c.m) 1 IK AK EK AK IK EK IC IK
Xét tam giác AQF có AE là đường cao ( vì MF AE EQ AE ), E
AE cũng là đường phân giác (c.m.t) do đó tam giác AQF cân tại A: Trang 21
Xét AQE và AQF, có: AQ=AF (Vì AQF
cân); FAE QAE (AE là phân giác); AE chung
Suy ra: AQE = AQF (c.g.c) 0
EQA EFA 90 (đ.p.c.m) 1 1 1 1
Bài 5 (1,0 điểm). Cho a,b, c là các số dương thỏa:
2.CMR : abc 1 a 1 b 1 c 8
Vì a,b, c là các số dương, nên: 1 1 1 1 1 1 AM GM b c bc 2 1 1 2 1 a 1 b 1 c 1 a 1 b 1 c 1 b 1 c
1 b1 c 1 AM GM 1 AM GM ca ab Tương tự: 2 b
c a; 2 1 1 1 1 c 1 a1 b
Nhân vế theo vế ba BĐT trên: 1 1 1 bc ca ab . . 8
a b c
b c. c a. 1 1 1 1 1 1 1
1 a1 b 1 abc 1
a b c 8 abc 1 1 1
1 a1 b1 c 8 a b c 1
a 1 b 1 c 1
Dấu “=” xảy ra khi và chỉ khi
a b c 1 2 abc 8
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO 10 THPT CHUYÊN BÌNH ĐỊNH
Năm học: 2021 – 2022
Môn: TOÁN (Chuyên Toán – Tin) – Ngày: 11/06/2021
Đề chính thức
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
-------------------- oOo --------------------
Bài 1. (2.0 điểm) æ x - y x + y ö ç ÷ 1 æ 1 ö = ç - ÷ ç ÷
1. Cho biểu thức: A . ç ÷ ç - ÷. çè x + y x - y ÷ ç ø èx y ÷ ø
Tính giá trị biểu thức A với x = 2021 + 2 505 , y = 2021- 2 505 . 1 1 1 1
2. Cho các số thực a , b , c ¹ 0 và a + b + c ¹ 0 thỏa mãn + + = . a b c a + b + c 1 1 1 1 Chứng minh rằng: + + = 2021 2021 2021 2021 2021 2021 . a b c a + b + c
Bài 2. (2.5 điểm)
1. Cho tập hợp A gồm 21 số tự nhiên khác nhau thỏa mãn tổng của 11 số bất kỳ lớn hơn tổng
của 10 số còn lại. Biết các số 101 và 102 thuộc tập hợp A . Tìm các số còn lại của tập hợp A . 2
2. Tìm tất cả các số nguyên dương x sao cho x - x + 13 là số chính phương. Trang 22
Bài 3. (1.5 điểm)
ìï 2 2xy - y + 2x + y = 10 ï
Giải hệ phương trình: íï . ï 3y + 4 -
2 y + 1 + 2 2x - 1 = 3 ïî
Bài 4. (3.0 điểm)
Cho tam giác ABC nội tiếp đường tròn tâm O , D là điểm bất kì thuộc cạnh BC ( D khác B và
C ). Gọi M , N lần lượt là trung điểm của các cạnh AB và AC . Đường thẳng MN cắt đường tròn
(O) tại P , Q (theo thứ tự P , M , N , Q ). Đường tròn ngoại tiếp tam giác BDP cắt AB tại I
(khác B ). Các đường thẳng DI và AC cắt nhau tại K .
a) Chứng minh 4 điểm A , I , P , K nằm trên một đường tròn. QA PD b) Chứng minh = . QB PK
c) Đường thẳng CP cắt đường tròn ngoại tiếp tam giác BDP tại G (khác P ). Đường thẳng CD
IG cắt đường thẳng BC tại E . Chứng minh khi D di chuyển trên đoạn BC thì tỉ số không CE đổi.
Bài 5. (1.0 điểm)
Cho a , b là các số dương thỏa mãn a + 2b ³ 3 . Tìm giá trị nhỏ nhất của biểu thức: 2 2 9 2
3a + a b + ab + (8 + a) 3 b 2 P = . ab
---------- HẾT ----------
ĐÁP ÁN THAM KHẢO – CHUYÊN TOÁN TIN – BÌNH ĐỊNH 2021 – 2022
Bài 1. (2.0 điểm) æ x - y x + y ö ç ÷ 1 æ 1 ö = ç - ÷ ç ÷
1. Cho biểu thức: A . ç ÷ ç - ÷. çè x + y x - y ÷ ç ø èx y ÷ ø
Tính giá trị biểu thức A với x = 2021 + 2 505 , y = 2021- 2 505 . 1 1 1 1
2. Cho các số thực a , b , c ¹ 0 và a + b + c ¹ 0 thỏa mãn + + = . a b c a + b + c 1 1 1 1 Chứng minh rằng: + + = 2021 2021 2021 2021 2021 2021 ( ) * . a b c a + b + c
1. Điều kiện: x > 0 ; y > 0 và x ¹ y . æ x - y x + y ö ç ÷ 1 æ
1 ö x - 2 xy + y - x - 2 xy - y y - x 4 = ç - ÷ ç ÷ Ta có: A . ç ÷ ç - = ÷ . = . çè x + y x - y ÷ ç ø èx y ÷ ø x - y xy xy Thay x = 2021 + 2 505 , y =
2021- 2 505 vào biểu thức đã thu gọn, ta được: 4 4 A = = = 4 . 2021 + 2 505. 2021 - 2 505 2021- 4.505 Trang 23 ì 4 ïï x = 2021 + 2 505 ï Vậy A =
(với x > 0 ; y > 0 và x ¹ y ) và A = 4 khi í . xy ïï y = 2021- 2 505 ïî 1 1 1 1 1 1 1 1 b + c b + c 2. Ta có: + + = Û - + + = 0 Û + = 0 . a b c a + b + c a a + b + c b c
a(a + b + c) bc æ 1 1 ö ç ÷ Û (b + c)ç + ÷= 0 ç çèa ÷
(a + b + c) bc ÷ ø 2
Û (b + c)(bc + a + ab + ca)= 0 (do a, b, c ¹ 0 và a+ b+ c ¹ 0 ) a é = - b ê
Û (b + c)(a + b)(c + a)= 0 Û b ê = - c ê . cê = - a ë ìï 1 1 1 1 1 1 1 ï + + = - + = ï 2021 2021 2021 2021 2021 2021 2021 ï a b c a a c c
Với a = - b , suy ra: í ; do đó ï ( ) * đúng. 1 1 1 ïï = = 2021 2021 2021 2021 2021 2021 2021 ïïî a + b + c a - a + c c
Tương tự trong hai trường hợp còn lại là: b = - c và c = - a thì ( ) * cũng đúng.
Do đó bài toán được chứng minh.
Bài 2. (2.5 điểm)
1. Cho tập hợp A gồm 21 số tự nhiên khác nhau thỏa mãn tổng của 11 số bất kỳ lớn hơn tổng
của 10 số còn lại. Biết các số 101 và 102 thuộc tập hợp A . Tìm các số còn lại của tập hợp A . 2
2. Tìm tất cả các số nguyên dương x sao cho x - x + 13 là số chính phương.
1. Giả sử A = {a ; a ; a ;...; a
a ; a ; a ;...; a Î ¥
a < a < a < ... < a 1 2 3 21} với 1 2 3 21 và 1 2 3 21 .
Từ đề, suy ra: a + a + ... + a > a + a + ...+ a
a > a - a + a - a + ...+ a - a 1 2 11 12 13 21 Û 1 12 2 13 3 21 11 ( ) 1 .
Vì a ; a ; a ;...; a Î ¥ a - a ³ 10 a - a ³ 10 a - a ³ 10 2 1 2 3 21 nên 12 2 ; 13 3 ; ... ; 21 11 ( ). Từ ( )
1 và (2), suy ra: a > 10 + 10 + ...+ 10 = 100 a 1 14444442 4444443
mà 1 là số nhỏ nhất trong các số của tập hợp A 10 sè 10 nên a = 101 3 1 ( ). Từ ( )
1 và (3), suy ra: a - a + a - a + ...+ a - a < 101 4 12 2 13 3 21 11 ( ).
Từ (2) và (4) suy ra: a - a = a - a = ... = a - a = 10 5 12 2 13 3 21 11 ( ). Ta có:
10 = a - a = a - a + a - a + ...+ a - a ³ 10 12 2 ( 12 11 ) ( 11 10 ) ( 3 2 ) .
Þ a - a = a - a = ... = a - a = 1 6 12 11 11 10 3 2 ( ). Vì a = 101 Î a = 102 7 1 mà 102 A Þ 2 ( ).
Từ (5), (6) và (7) suy ra A = {101; 102; 103;...; 12 } 1 . 2 2
2. Theo đề, đặt x - x + 13 = a (với x , a + Î ¢ ). Trang 24 2 2 2 2
Û 4x - 4x + 52 = 4a Û (2a) - (2x - ) 1 = 51 Û (2a - 2x + ) 1 (2a + 2x - ) 1 = 51. Vì x , a +
Î ¢ Þ 2a- 2x + 1Î ¢ ; 2a 2x 1 + + -
Î ¢ và 2a- 2x + 1< 2a + 2x - 1. Do đó ta có bảng sau: 2a + 2x - 1 51 17 2a- 2x + 1 1 3 a 13 5 x 13 4 thỏa thỏa
Vậy số cần tìm là: x Î {4 ;1 } 3 .
Bài 3. (1.5 điểm)
ìï 2 2xy - y + 2x + y = 10 ï ( ) 1 ï
Giải hệ phương trình: íï . ï 3y + 4 -
2 y + 1 + 2 2x - 1 = 3 (2) ïî 1 Điều kiện: x ³ ; y ³ 0 . 2 2 Ta có: ( )
1 Û 2x - 1+ 2 y. 2x - 1 + y = 9 Û ( 2x - 1+ y) = 9
Û 2x - 1 + y = 3 (do 2x - 1 + y ³ 0 ). Û 2x - 1 = 3- y ( ) * . Thay 2x - 1 = 3-
y vào (2) ta được: 3y + 4 -
2y + 1 + 6- 2 y = 3 Û 2 y -
3y + 4 + 2y + 1- 3 = 0 y é - 4 = 0 ( ) 3 y - 4 2(y - 4) ê Û + = 0 Û ê 1 2 . 2 y ê + 3y + 4 2y + 1 + 3 + = 0 (4) 2 ê ê y + 3y + 4 2y + 1 + 3 ë
Từ (3) suy ra y = 4 (thỏa), thay vào ( )
* suy ra 2x - 1 = 1 Û x = 1 (thỏa). 1
Nhận thấy VT > 0 với mọi x ³
; y ³ 0 Þ phương trình (4) vô nghiệm. (4) 2
Vậy nghiệm của hệ phương trình đã cho là: (x ; y)= (1;4).
Bài 4. (3.0 điểm)
Cho tam giác ABC nội tiếp đường tròn tâm O , D là điểm bất kì thuộc cạnh BC ( D khác B và
C ). Gọi M , N lần lượt là trung điểm của các cạnh AB và AC . Đường thẳng MN cắt đường tròn
(O) tại P , Q (theo thứ tự P , M , N , Q ). Đường tròn ngoại tiếp tam giác BDP cắt AB tại I
(khác B ). Các đường thẳng DI và AC cắt nhau tại K .
a) Chứng minh 4 điểm A , I , P , K nằm trên một đường tròn. QA PD b) Chứng minh = . QB PK Trang 25
c) Đường thẳng CP cắt đường tròn ngoại tiếp tam giác BDP tại G (khác P ). Đường thẳng CD
IG cắt đường thẳng BC tại E . Chứng minh khi D di chuyển trên đoạn BC thì tỉ số không CE đổi. · ·
a) Vì tứ giác APBC nội tiếp Þ PAC + PBC = 180° ( ) 1 . · ·
Vì tứ giác BDIP nội tiếp Þ PID + PBC = 180° (2). · · Từ ( )
1 và (2), suy ra: PID = PAC . · · Lại có:
PID + PIK = 180° ; · ·
PAC + PAK = 180° . Do đó: · ·
PIK = PAK ; mà hai góc này cùng
nhìn cạnh PK Þ tứ giác AIPK nội tiếp
hay 4 điểm A , I , P , K nằm trên 1 đường tròn. · · · ·
b) Ta có: APK = AIK = BID = BPD .
Xét D PBD và D PAK , ta có: · · PBD = PAK · ·
(cmt); APK = BPD (cmt).
Þ DPBD # DPAK (g – g) Þ PB PD = (3). PA PK
Vì tứ giác APBQ nội tiếp, suy ra: ìï PB MP ï = ïïï QA MA PB QB í = ï Þ . 1 Þ QB MB ï QA PA ï = ïïî PA MP PB QA = (4). PA QB QA PD Từ (3) và (4), suy ra: = . QB PK · ·
c) Trên AB xác định điểm H sao cho APH = KPI . · ·
Vì tứ giác AIPK nội tiếp, nên KPI = BAC . ·
Lại có A , P và BAC không đổi nên H là điểm cố định. KI KP
Dễ dàng chứng minh được D KPI # D APH (g – g) Þ = (5). AH AP KP KD
Dễ dàng chứng minh được D PKD # D PAB (g – g) Þ = (6). AP AB KD KI KD AB Từ (5) và (6) suy ra: = Þ = (7). AB AH KI AH CD KD · · ·
Ta có: PGI = PBI = PCA nên GI AC hay IE AC Þ = (8). CE KI Trang 26 CD AB AB CD Từ (7) và (8) suy ra = mà không đổi nên không đổi. CE AH AH CE
Bài 5. (1.0 điểm)
Cho a , b là các số dương thỏa mãn a + 2b ³ 3 . Tìm giá trị nhỏ nhất của biểu thức: 2 2 9 2
3a + a b + ab + (8 + a) 3 b 2 P = . ab 2 2 9 2 3a + a b + ab + (8 + a) 3 b 2 3a 9b 8 2 b 2 Ta có: P = = + a + + + b ab b 2 a 2 8b 4 .2 b b
4b(3- a) 12b
Theo đề a + 2b ³ 3 Þ 2b ³ 3- a Þ = = = - 4b . a a a a Do đó: 2 3a 9b 8b 2 3a 9b 12b 2 3a 12b 2 3b P = + a + + + b ³ + 3- 2b + + - 4b + b = + + b - + 3 b 2 a b 2 a b a 2 2 3a 12b æ 3ö 39 39 231 ³ 2. . + b ç ÷ - ç ÷ + ³ 12 + = . b a çè 4÷ø 16 16 16 ìï a, b > 0 ïïï 3a 12b 3 Đẳ ï
ng thức xảy ra khi và chỉ khi í = a = 2b = ï Û . b a ï 2 ïï a + 2b = 3 ïî 231 3 æ 3ö
Vậy giá trị nhỏ nhất của P bằng khi (a ;b) ç = ; ÷ ç ÷. 16 çè2 4÷ø
---------- CHÚC CÁC EM HỌC TỐT ----------
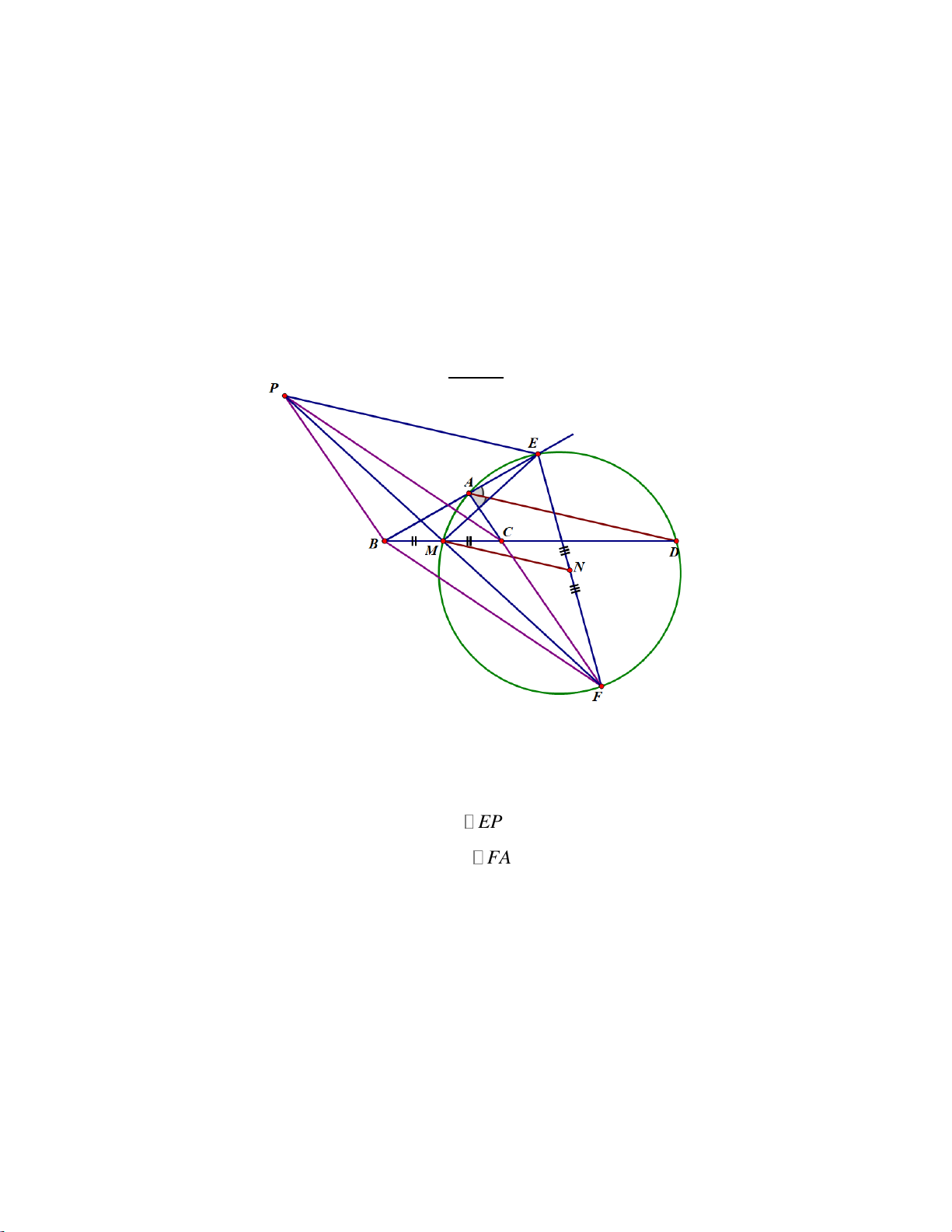
ĐỀ THI TUYỂN SINH 10 CHUYÊN TOÁN TỈNH BÌNH DƯƠNG – 2021-2022 Câu 1 ( 2 điểm )
√𝑥+2√𝑥−1 + √𝑥−2√𝑥−1 a/ rút gọn P= với x≥2
√𝑥+√2𝑥−1− √𝑥−√2𝑥−1 1
b/ cho x là số thực dương thỏa mãn: 𝑥2 + = 7. 𝑥2 1
Tính giá trị của A=𝑥7 + 𝑥7 Câu 2 ( 2điểm )
a/ với a,b,c là độ dài 3 cạnh của tam giác.
Chứng minh pt sau vô nghiệm: 𝑥(𝑐2(x − 1) + (𝑎2 − 𝑏2) + 𝑏2 = 0 với x thuộc R b/ giải pt:
(𝑥2 − 6𝑥 + 11)√𝑥2 − 𝑥 + 1 = 2(𝑥2 − 4𝑥 + 7)√𝑥 − 2 Câu 3: (3 điểm ) Trang 27
a/ cho 3 số nguyên a,b,c thỏa 𝑎 = 𝑏 − 𝑐 = 𝑏/𝑐 . cm rằng ( a+b+c) có giá trị là lập phương của 1 số nguyên
b/ cho x,y,z >0 thỏa xy + yz +zx =1 . chứng minh : 10𝑥2 + 10𝑦2 + 𝑧2 ≥ 4. Dấu “=” xảy ra khi nào ? Câu 4: (3 điểm )
Cho hình thoi ABCD ( AC>BD). Gọi O là giao điểm của AC và BD. (O) nội tiếp
hình thoi ABCD, tiếp xúc các cạnh AB, BC, CD, DA lần lượt tại E,F,G,H. Lấy K
trên đoạn HA và L trên đoạn AE sao cho KL tiếp xúc (O)
a/ cm : 𝑔ó𝑐 𝐿𝑂𝐾 = 𝑔ó𝑐 𝐿𝐵0 𝑣à 𝐵𝐿. 𝐷𝐾 = 𝑂𝐵2
b/ đường tròn ngoại tiếp tam giác CFL cắt cạnh AB tại M ( khác L ), đường tròn
ngoại tiếp tam giác CKG cắt cạnh AD tại N ( khác K ). Chứng minh K,L,M,N cùng thuộc đường tròn
c/ lấy P,Q tương ứng trên đoạn FC và GC sao cho LP//KQ. Chứng minh PQ tiếp xúc (O)
………………………………………………………………………..
Hướng dẫn giải : TOÁN CHUYÊN TỈNH BÌNH DƯƠNG NĂM HỌC 2021-2022 Câu 1 a)
√𝑥+2√𝑥−1 + √𝑥−2√𝑥−1
|√𝑥−1+1|+|√𝑥−1−1| P= =
√𝑥+√2𝑥−1− √𝑥−√2𝑥−1 1
√ (|√2𝑥−1+1|−|√2𝑥−1−1|) 2
Ta có x≥2 ⇔ x-1 ≥ 1 ⇔ √𝑥 − 1 ≥ 1
Do đó P=√2 ⋅ √𝑥−1+1+ √𝑥−1−1 = √2(𝑥 − 1)
√2𝑥−1+1− √2𝑥−1+ 1 b) 1 1 1 1 1 1 Ta có (𝑥2 + ) (𝑥5 + ) = 𝑥7 + + 𝑥3 + ⇒ 𝑥7 + = 7(𝑥5 + ) − 𝑥2 𝑥5 𝑥7 𝑥3 𝑥7 𝑥5 1 (𝑥3 + ) (1) 𝑥3 1 1 1 1 1 1 Ta lại có: (𝑥2 + )(𝑥3 + )= 𝑥5 + + 𝑥 + ⇒ 𝑥5 + = 7(𝑥3 + ) − (𝑥 + 𝑥2 𝑥3 𝑥5 𝑥 𝑥5 𝑥3 1 ) (2) 𝑥 1 1 1 1 1 1 (𝑥2 + ) (𝑥 + ) = 𝑥3 + + 𝑥 + ⇒ 𝑥3 + = 6 (𝑥 + ) (3) 𝑥2 𝑥 𝑥3 𝑥 𝑥3 𝑥 Từ (1), (2) và (3) Ta có: 1 1 1 1 1
𝑥7 + = 7 [ 7(𝑥3 + ) – (𝑥 + ) ] − 6 (𝑥 + ) = 281(𝑥 + ) 𝑥7 𝑥3 𝑥 𝑥 𝑥 1 1 1
Ta lại có: (𝑥 + ) 2=𝑥2 + + 2 = 9 ⇒ (𝑥 + ) = ± 3 𝑥 𝑥2 𝑥 1 1
Mà x là số nguyên dương nên (𝑥 + ) > 0 Nên (𝑥 + ) = 3 𝑥 𝑥 Trang 28 1 Vậy 𝑥7 + = 843 𝑥7 Câu 2: a)
Phương trình đã cho tương đương với
𝑐2𝑥2 + (𝑎2 − 𝑏2 − 𝑐2)𝑥 + 𝑏2 = 0
Phương trình trên có biệt số 𝛥 = (𝑎2 − 𝑏2 − 𝑐2)2 − 4𝑏2𝑐2 = 𝑎4 + 𝑏4 + 𝑐4 −
2𝑎2𝑏2 − 2𝑏2𝑐2 − 2𝑎2𝑐2 = (𝑎2 + 𝑏2 + 𝑐2)2 − 4(𝑎2𝑏2 + 𝑏2𝑐2 + 𝑎2𝑐2) < 0 b) Đkxđ: 𝑥 ≥ 2.
Phương trình đã cho tương đương với
[(𝑥2 − 𝑥 + 1) − 5(𝑥 − 2)]√𝑥2 − 𝑥 + 1 = 2[(𝑥2 − 𝑥 + 1 − 3(𝑥 − 2)]√𝑥 − 2
Đặt 𝑎 = √𝑥2 − 𝑥 + 1 , 𝑏 = √𝑥 − 2. (𝑎, 𝑏 ≥ 0). Phương trình trở thành
𝑎3 − 2𝑎2𝑏 − 5𝑎𝑏2 + 6𝑏3 = 0
⇔ (𝑎 + 2𝑏)(𝑎 − 3𝑏)(𝑎 − 𝑏) = 0
- TH1: 𝑎 = −2𝑏 (vô lý vì lúc này 𝑥2 − 𝑥 + 1 = 𝑥 − 2 = 0(vô nghiệm)) - TH2: 𝑎 = 𝑏
⇔ 𝑥2 − 𝑥 + 1 = 𝑥 − 2
⇔ (𝑥 − 1)2 = −2 (vô nghiệm) - TH3: 𝑎 = 3𝑏
⇔ 𝑥2 − 𝑥 + 1 = 9(𝑥 − 2) ⇔ 𝑥2 − 10𝑥 + 19 = 0 ⇔ 𝑥 = 5 − √6(nhận) 𝑥 = 5 + √6(nhận) Vậy 𝑥 = 5 ± Câu 3: a)
Điều kiện để cho tương đương với
𝑏 = 𝑎 + 𝑐 = 𝑎𝑐.
⇒ 𝑎𝑐 − 𝑎 − 𝑐 + 1 = 1
⇔ (𝑎 − 1)(𝑐 − 1) = 1
Vì 𝑎, 𝑐 ∈ 𝕫 và 𝑐 > 0 nên ta phải có 𝑎 − 1 = 𝑐 − 1 = 1, hay 𝑎 = 𝑐 = 2.
Điều này dẫn tới 𝑏 = 4. Trang 29
Ta có 𝑎 + 𝑏 + 𝑐 = 8 = 23, là một số lập phương. Vậy ta có đpcm. b)
Bất đẳng thức đề cho tương đương với
10𝑥2 + 10𝑦2 + 𝑧2 ≥ 4(𝑥𝑦 + 𝑦𝑧 + 𝑥𝑧)
⇔ 12𝑥2 + 12𝑦2 + 3𝑧2 ≥ 2(𝑥 + 𝑦 + 𝑧)2 𝑥2 𝑦2 𝑧2
⇔ 1 + 1 + 1 ≥ 2(𝑥 + 𝑦 + 𝑧)2 (1) 12 12 3
Theo bất đẳng thức Bunyakovsky dạng cộng mẫu, ta có 𝑥2 𝑦2 𝑧2 (𝑥 + 𝑦 + 𝑧)2 + + ≥ = 2(𝑥 + 𝑦 + 𝑧)2 1 1 1 1 12 12 3 2
Vậy (1) đúng, ta có đpcm.
Dấu “=” xảy ra ⇔ 3𝑥 = 3𝑦 = 12𝑧 ∨ 𝑥𝑦 + 𝑦𝑧 + 𝑥𝑧 = 1 4 1
⇔ 𝑧 = ∨ 𝑥 = 𝑦 = . 3 3 Câu 4 a) KL ∩ (𝑜) = 𝑇
OK là phân giác ∠𝑇𝑂𝐻
OL là phân giác ∠𝑇𝑂𝐸 ⇒ ∠𝐿𝑂𝐾 = ½ ∠𝐻𝑂𝐸
Dễ dàng chứng minh OHAE là tứ giác nội tiếp
⇒ ∠𝐻𝑂𝐸 = 180° − ∠𝐻𝐴𝐸
Do đó ∠𝐿𝑂𝐾= 90° − ∠𝑂𝐴𝐵
= ∠𝐵𝑂𝐿 (do ABCD là hình bình hành)
Xét 𝛥𝐾𝐿𝐶 và 𝛥𝑂𝐿𝐵: ∠𝐿𝑂𝐾 = ∠𝑂𝐵𝐿
∠𝐾𝐿𝑂 = ∠𝑂𝐿𝐵 (1)
Do đó 𝛥𝐾𝐿𝐶 ∼ 𝛥𝑂𝐿𝐵 ⇒ ∠𝑂𝐾𝐿 = ∠𝐵𝑂𝐿 = ∠𝑂𝐾𝐷
Dễ thấy 𝛥𝐴𝐵𝐷 cân tại A ⇒ ∠𝑂𝐵𝐿 = ∠𝑂𝐷𝐾
Xét 𝛥𝐵𝐿𝑂 và 𝛥𝐷𝑂𝐾: ∠𝑂𝐵𝐿 = ∠𝑂𝐷𝐾
∠𝑂𝐾𝐿 = ∠𝑂𝐾𝐷 Trang 30 Do đó 𝐵𝐿 𝑂𝐵
𝛥 𝐵𝐿𝑂 ∼ 𝛥𝐷𝑂𝐾 ⇒ =
⇒ 𝐵𝐿. 𝐷𝐾 = 𝑂𝐵. 𝑂𝐷 = 𝑂𝐵2 ( do ABCD là 𝑂𝐷 𝐷𝐾 hình bình hành ) (2) b)
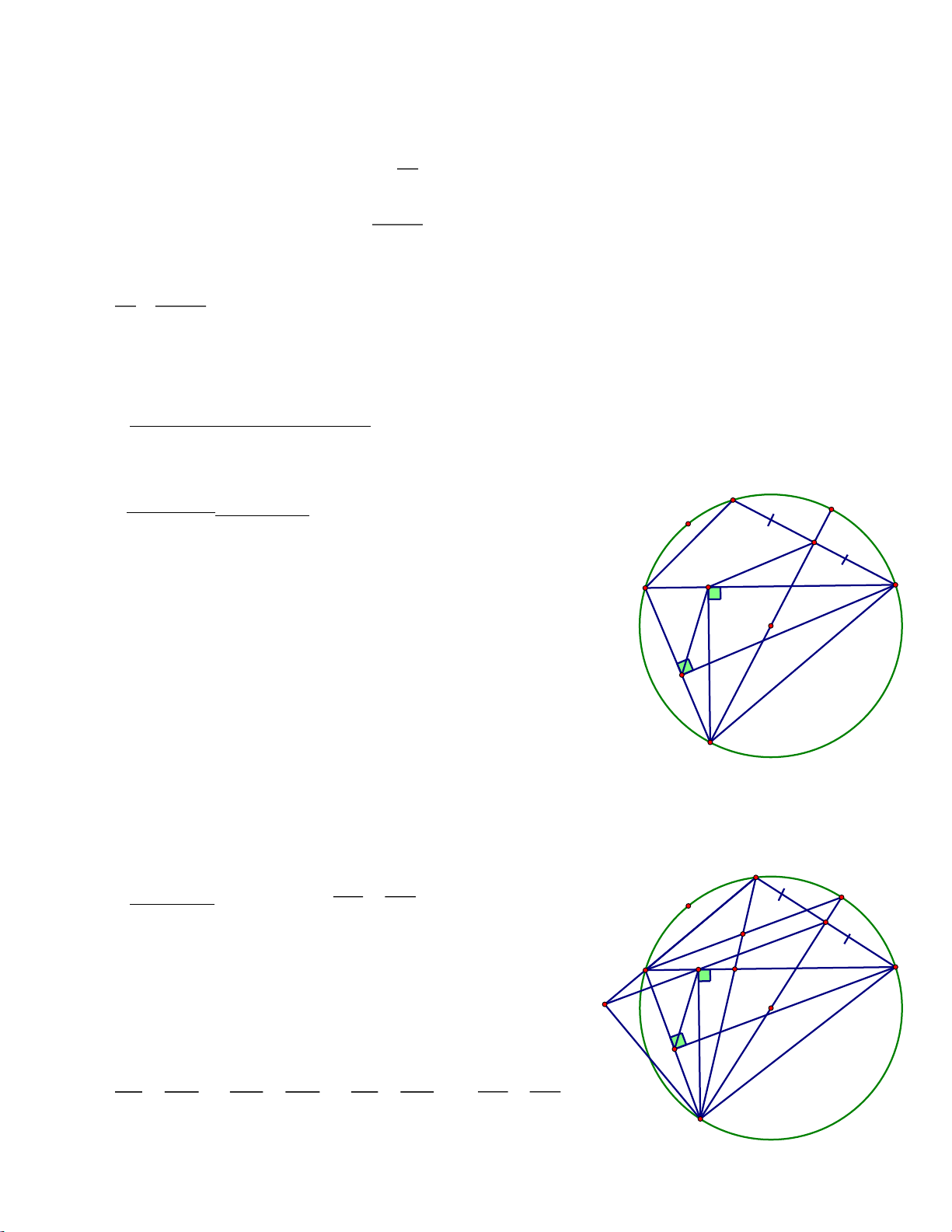
Ta có: MLFC nội tiếp ⇒ 𝐵𝐿. 𝐵𝑀 = 𝐵𝐹. 𝐵𝐶 = 𝑂𝐵2( Hệ thức lượng ) (3) 𝐵𝐿 𝐵𝑂 ⇒ =
Mà ∠𝑂𝐵𝑀 chung nên 𝛥𝐵𝐿𝑂 ∼ 𝛥𝐵𝑂𝑀 𝐵𝑂 𝐵𝑀
⇒ ∠𝑀𝑂𝐵 = ∠𝐵𝐿𝑂 (4) Từ (2) và (3) ⇒ DK=BM
Lại có: OB=OD và ∠𝑂𝐵𝑀 = ∠𝑂𝐷𝐾
Do đó 𝛥𝐵𝑀𝑂 ∼ 𝛥𝐷𝐾𝑂 ⇒ OM = OK và ∠𝐵𝑂𝑀 = ∠𝐷𝑂𝐾
Lại có AB = AC nên AM = AK ⇒ 𝛥𝐴𝑀𝐾 ∼ 𝛥𝐴𝐵𝐶 ⇒ MK // BC
⇒ ∠𝐾𝑀𝑂 = ∠𝑀𝑂𝐵 (5)
Từ (1), (4) và (5) ta có: ∠𝐾𝑀𝑂 = ∠𝐾𝐿𝑂 ⇒ KMLO nội tiếp (w).
Chứng minh tương tự ta có: KMON nội tiếp (w)
Do đó K, M, L, N thuộc đường tròn (w). c)
Dễ dàng chứng minh: 𝛥𝐵𝐿𝑃 ∼ 𝛥𝐷𝑄𝐾 𝐵𝐿 𝐵𝑃 ⇒ =
⇒ 𝐵𝑃. 𝐷𝑄 = 𝐵𝐿. 𝐷𝐾(6) 𝐷𝑄 𝐷𝐾 𝐵𝑃 𝐵𝑂
Từ (2) và (6) ⇒ 𝐵𝑃. 𝐷𝑄 = 𝑂𝐵2 ⇒ = 𝐵𝑂 𝐷𝑄
Lại có: ∠𝐵𝑂𝑃 = ∠𝐵𝐿𝑂 = ∠𝐵𝑂𝑀 = ∠𝐷𝑂𝐾 = 𝐷𝑂𝑄
Do đó 𝛥𝐵𝑃𝑂 ∼ 𝛥𝐷𝑂𝑄
Vẽ tiếp tuyến PS của (O), ta cần chứng minh S ≡ Q
Tương tự như trên ta chứng minh được 𝛥𝐵𝑃𝑂 ∼ 𝛥𝐷𝑂𝑆 Do đó 𝐷𝑂 𝐷𝑆
𝛥𝐷𝑂𝑆 ∼ 𝛥𝐷𝑂𝑄 ⇒ = ⇒ DS = DQ ⇒ S ≡ Q. 𝐷𝑂 𝐷𝑄 Vậy ta có đpcm. Trang 31
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM 2021 BÌNH PHƯỚC
MÔN THI: TOÁN CHUYÊN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 9/6/2021
(Đề thi gồm có 01 trang) 2 1 1 x 2 x x x x x 1
Câu 1. (1,5 điểm) Cho biểu thức A : x x x x x 1
a) Rút gọn biểu thức . A
b) Tìm x nguyên để A nhận giá trị nguyên. Câu 2. (2,0 điểm)
a) Giải phương trình: 2
2x 2x 3 3x 6x 1 2
x xy x y x 2 2 4 3 4 4 9
1 x 2xy x 2 y
b) Giải hệ phương trình:
x 1 x 2y 2x 2y 5
Câu 3. (1,5 điểm) Cho phương trình: 2 2
x 2(m 3)x 3m 8m 5 0 , với m là tham số.
a) Tìm m để phương trình có 2 nghiệm trái dấu.
b) Tìm m để phương trình có 2 nghiệm x ; x phân biệt thỏa mãn điều kiện: 1 2 2 2 x 2x
3x x x x . 1 2 1 2 1 2
Câu 4. (3,0 điểm) Cho tam giác nhọn ABC AB AC nội tiếp đường tròn O , D là
điểm chính giữa trên cung nhỏ BC của đường tròn O, H là chân đường cao kẻ từ A của tam giác .
ABC Hai điểm K , L lần lượt là hình chiếu vuông góc của H lên AB và . AC
a) Chứng minh A . L CB A . B K . L
b) Lấy điểm E trên đoạn thẳng AD sao cho BD DE . Chứng minh E là tâm đường tròn nội tiếp tam giác . ABC
c) Đường thẳng KL cắt đường tròn O tại hai điểm M , N ( K nằm giữa M , L ).
Chứng minh AM AN AH. Câu 5. (1,0 điểm)
a) Tìm nghiệm nguyên của phương trình: 2x y x y 32x y 5 x y 22.
b) Cho hai số tự nhiên a, b thỏa mãn 2 2
2a a 3b .
b Chứng minh rằng 2a 2b 1là số chính phương.
Câu 6. (1,0 điểm) Cho a, ,
b c là các số dương. Chứng minh rằng: 3 a b a) a . 2 2 a b 2 3 3 3 a b c
a b c b) . 2 2 2 2 2 2
a ab b
b bc c
c ca a 3
............HẾT........... Trang 32
Thí sinh không được sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KỲ THI TUYỂN SINH BÌNH PHƯỚC LỚP 10 NĂM 2021
(Hướng dẫn chấm gồm 07 trang)
MÔN THI: TOÁN CHUYÊN
Lưu ý: - Điểm toàn bài lấy điểm lẻ đến 0,125.
- Học sinh giải cách khác với đáp án thì giám khảo xem xét, nếu đúng vẫn
cho điểm tối đa. Câu Nội dung Điểm
2 x 2 x x x x x 1 1 1 1,5 1
Cho biểu thức A : . x x x x x 1
a) Rút gọn biểu thức A. 1,0 0,25
ĐKXĐ: x 0, x 1
x 1x x x x 1 1 x x 1 Ta có x x x x 1 x
x 1x x x x 1 1 x x 1 0,5 x x x x 1 x
x x x 2 2 2 1 2 1 2 x 1 x 1
x 1 x 1 x 1 2 x x x x x 1 1 1 x 1 0,25 Vậy A : x x x 1 x 1
b) Tìm x nguyên để A nhận giá trị nguyên 0,5 x 1 2 Ta có A 1 0,125 x 1 x 1
Để A nhận giá trị nguyên thì x 1 là ước của 2 . Hay x 1 2; 2;1; 1 . x 1 2 x 1 l 0,25 x 1 1
x 0 x 0 l Suy ra
x 1 2 x 3 x 9n
x 1 1 x 2 x 4 n Trang 33
Vậy có 2 giá trị x 4; x 9 thì A nguyên. 0,125
a) Giải phương trình: 2
2x 2x 3 3x 6x 1.
b) Giải hệ phương trình: 2,0 2 2
x xy x y x 2 2 4 3 4 4 9
1 x 2xy x 2 y
x 1 x 2y 2x 2y 5.
a) Giải phương trình: 2
2x 2x 3 3x 6x 1. 1,0 ĐKXĐ: 3 x 0,125 2 Ta có 2 0,25
Pt x x x x
x x x x x 2 2 2 2 3 2 2 3 4 8 4 2 3 2 2
x 2x 3 2x 2
2x 3 x 2
x 2x 3 2 x 2 2x 3 3 x 2 x 2 x 2 x 1 (n) 2
x 2x 1 0 2 0,5 x 2 3 x 3 x 1 (n) 2 9
x 10x 1 0 1
x (l) 9
Kết hợp với điều kiện phương trình có nghiệm là x 1 . 0,125
b) Giải hệ phương trình: 2
x xy x y x 2 2 4 3 4 4 9
1 x 2xy x 2 y 1,0
x 1 x 2y 2x 2y 5. x 2
1 x 2xy x 2 y 0 Điề u kiện: x 1 0 0,125
x 2y 0
2x 2y 5 0 Ta có phương trình (2)
x 1 2 x
1 x 2 y x 2 y 2 x y 5 0,25 2 x
1 x 2y 4 x
1 x 2y 2 x
1 x 2y 2
4 x 2xy x 2y 4 (*) Ta có phương trình (1) 0,25 2
x xy x y x x 2 2 2 2 4 9
1 x 2xy x 2 y Trang 34
8 x 4 36x 1 36x 1 x 4 x 4 x 4 x 4
x 2 (n) 36 x 2
1 x 8x 16 2
x 28x 52 0
x 26 (n)
Với x 2 thay vào (*) ta có: 1
pt (*) 4 4 y 2 2 y 4 6 y 2 y (thỏa mãn). 3 0,25
Với x 26 thay vào (*) ta có: 349
(*) 676 52 y 26 2 y 4 54 y 698 y .(thỏa mãn). 27 x 2 x 26 0,125
Kết luận: Hệ có 2 nghiệm là: 1 và 349 . y y 3 27 Cho phương trình: 2 2
x 2(m 3)x 3m 8m 5 0 , với m là tham số.
a) Tìm m để phương trình có 2 nghiệm trái dấu. 3 1,5
b) Tìm m để phương trình có 2 nghiệm x ; x phân biệt thỏa mãn điều 1 2 kiện 2 2
x 2x 3x x x x 1 2 1 2 1 2
a) Tìm m để phương trình có 2 nghiệm trái dấu. 0,75
Để phương trình có 2 nghiệm trái dấu thì 0,25 2
x .x 0 3m 8m 5 0 m 1 3m 5 0 1 2 m 1 m 1 0 5 m 3 m 5 0 3 5 1 m 0,375 m 1 0 m 1 3 3 m 5 0 5 m 3 5 Vậy 1 m
thì thỏa yêu cầu bài toán. 0,125 3
b) Tìm m để phương trình có 2 nghiệm x ; x phân biệt thỏa mãn điều 1 2 kiện 2 2
x 2x 3x x x x 0,75 1 2 1 2 1 2
Phương trình có 2 nghiệm phân biệt thì
m 32 2 2 2
3m 8m 5 0 m 6m 9 3m 8m 5 0 0,125 2 2
m 2m 4 0 1 m 2
x x 2(m 3) (1)
Theo định lý Vi-et ta có: 1 2 0,125 2
x x 3m 8m 5 (2) 1 2 Theo đề ta có 0,25 Trang 35 x x 0 2 2
x 2x 3x x x x x x x 2x x x 1 2 1 2 1 2 1 2 1 2 1 2 1 2
x 2x 1 0 1 2
TH1: x x 0 (loại vì x x ). 1 2 1 2 TH2:
x 2x 1 0 , kết hợp với (1) ta có hệ: 1 2 2m 7 x
x x 2m 3 2 3x 2m 7 1 2 2 3
x 2x 1 0 x 2x 1 4m 11 1 2 1 2 x 1 3
Thay x ; x tìm được vào (2) ta có: 1 2
4m 11 2m 7 0,25 2 .
3m 8m 5 3 3
m 2 l 2
19m 22m 32 0 16 m tm 19 16
Kết hợp với điều kiện ta có m
thì thỏa yêu cầu bài toán. 19
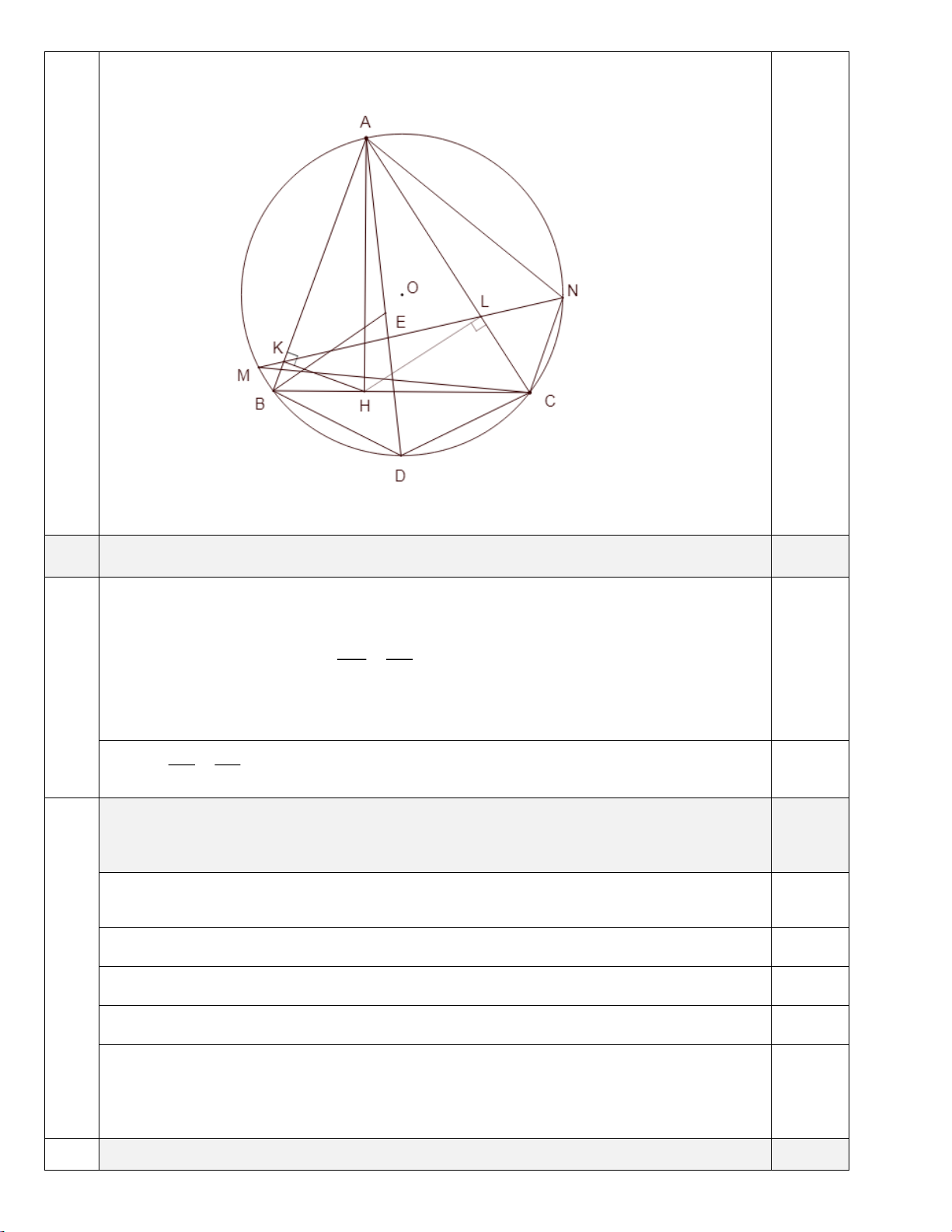
Cho tam giác nhọn ABC AB AC nội tiếp đường tròn O , D là điểm chính
giữa trên cung nhỏ BC của đường tròn O, H là chân đường cao vẽ từ A của tam giác .
ABC Hai điểm K , L lần lượt là hình chiếu vuông góc của H lên AB và AC . 4 3,0
a) Chứng minh A . L CB A . B KL .
b) Lấy điểm E trên đoạn thẳng AD sao cho BD DE . Chứng minh E là
tâm đường tròn nội tiếp tam giác . ABC
c) Đường thẳng KL cắt đường tròn O tại hai điểm M , N ( K nằm giữa
M , L ). Chứng minh AM AN AH. Trang 36
a) Chứng minh A . L CB A . B KL . 1
Xét hai tam giác AKL và ACB , có: + A chung AK AL + 2
AK.AB AH . AL AC . 0,5 AC AB
Suy ra hai tam giác AKL và ACB đồng dạng. AL KL Suy ra A . L CB A . B . KL 0,5 AB CB
b) Lấy điểm E trên đoạn thẳng AD sao cho BD DE . Chứng minh E
là tâm đường tròn nội tiếp tam giác . ABC 1,0
Ta có D là điểm chính giữa trên cung nhỏ BC nên AE là đường phân giác trong 0,25
của góc A của tam giác . ABC (*)
+ Tam giác DBE cân tại D nên : BED EBD 1 . 0,125
+ BED BAD ABE BCD ABE DBC ABE 2 . 0,25
+ Ta có EBD DBC EBC 3 0,125
Từ (1), (2), (3) suy ra ABE EBC hay BE là phân giác trong của góc B của tam giác ABC * * . 0,25
Từ (*) và (**) suy ra E là tâm đường tròn nội tiếp tam giác . ABC
c) Đường thẳng KL cắt đường tròn O tại hai điểm M , N ( K nằm giữa 1,0 Trang 37
M , L ). Chứng minh AM AN AH.
+ Hai tam giác AKL và ACB đồng dạng. 1 1
Suy ra ALK ABC sdAM sd NC sd AC 2 2 1 0.5
sd AM sd NC 1
sd AN sd NC 2 2
sd AM sd AN AN AM 4
+ Chứng minh được hai tam giác ALN và ANC đồng dạng vì có góc A chung
và ANL ACN (cùng chắn 2 cung bằng nhau). 0,5 AL AN Suy ra 2 AN A . L AC. Mà 2 A .
L AC AH AN AH 5 AN AC
Từ (4) và (5) ta suy ra AM AN AH.
a) Tìm nghiệm nguyên của phương trình:
2x yx y32x y5x y 22 1,0 5
b) Cho hai số tự nhiên a, b thỏa mãn 2 2
2a a 3b .
b Chứng minh rằng
2a 2b 1 là số chính phương.
a) Tìm nghiệm nguyên của phương trình:
2x yx y32x y5x y 22 0,5
Ta có 2x y x y 32x y 5 x y 22
2x y x y 3 5 x y 3 7 0,125
2x y 5x y 3 7
Vì 7 1.7 7.1 1 . 7 7 .
1 nên ta có 4 trường hợp xảy ra. 0,125 10 x
2x y 5 1 TH1: 3 (loại).
x y 3 7 2 y 3 0,125 10 x
2x y 5 7 TH2: 3 (loại).
x y 3 1 16 y 3
2x y 5 1 x 2 TH3: (thỏa mãn)
x y 3 7 y 8
2x y 5 7 x 2 0,125 TH4: (thỏa mãn)
x y 3 1 y 2
Vậy phương trình đã cho có hai nghiệm ; x y là 2 ;8 và 2 ;2
b) Cho hai số tự nhiên a, b thỏa mãn 2 2
2a a 3b .
b Chứng minh rằng 0,5
2a 2b 1 là số chính phương. Trang 38 Ta có 2 2
a a b b a b a b 2 2 3 2 2 1 b *
Gọi d a ,
b 2a 2b 1 với * d a b d 0,25 Suy ra
a b2a 2b 2 2 2
b d b d. a b 1 d 2 2 1 d
Vì a b d a d 2a 2b d mà 2a 2b
1 d nên 1 d d 1 0,125 Do đó a ,
b 2a 2b
1 1. Từ (*) ta được a b và 2a 2b 1 là số chính
phương. Vậy 2a 2b 1 là số chính phương. 0,125
Cho a,b, c là các số dương. Chứng minh rằng: 3 a b a) 1,0 6 a . 2 2 a b 2 3 3 3 a b c
a b c b) . 2 2 2 2 2 2
a ab b
b bc c
c ca a 3 3 a b a) a . 0,5 2 2 a b 2 a 2 2 a b 2 3 2 ab a ab Ta có a . 2 2 2 2 2 2 a b a b a b 0,25 2 2 ab ab b
Theo BĐT Cauchy ta có a a a . 2 2 a b 2ab 2 0,25 3 3 3 a b c
a b c b) . 0,5 2 2 2 2 2 2
a ab b
b bc c
c ca a 3 3 3 Tương tự b c c a theo câu a) ta có : b , c . 2 2 b c 2 2 2 c a 2
Cộng vế theo vế ba bất đẳng thức trên ta có: 0,125 3 3 3 a b c
a b c . 2 2 2 2 2 2 a b b c c a 2 3 3 3 a a 2 a Ta có: . . 2 2 2 2 2 2
a ab b a b 0,125 2 2 3 a b a b 2 3 3 3 3 Tương tự b 2 b c 2 c ta có . , . . 2 2 2 2
b bc c 3 b c 2 2 2 2
c ca a 3 c a 0,125
Cộng vế theo vế ba bất đẳng thức trên ta có: 3 3 3 a b c 2 2 2 2 2 2
a ab b
b bc c
c ca a 0,125 3 3 3 2 a b c
a b c . 2 2 2 2 2 2 3 a b b c c a 3 Trang 39 HẾT.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH 10 THPT CHUYÊN CÀ MAU
NĂM HỌC 2021 – 2022 ĐỀ CHÍNH THỨC
Môn thi: Toán (Chuyên)
(Đề thi có hai 02 trang) Ngày thi: 11/6/2021
Thời gian: 150 phút (không kể thời gian giao đề)
x x 1 x x 1 2x 4 x 2
Bài 1: (1,0 điểm) Cho biểu thức: A :
(với x 0; x 0) x x x x x 1
a) Rút gọn biểu thức A.
b) Tìm các số nguyên x để biểu thức A có giá trị nguyên
Bài 2: (1,0 điểm) Giải phương trình: 2 2 x x x x 2 2 2 4
3 1 x 7x,
(với x 0 hoặc x 4) 1
Bài 3: (1,5 điểm) Trong mặt phẳng tọa độ vuông góc Oxy cho parabol (P): 2 y x 3 a) Vẽ đồ thị (P).
b) Tìm tọa độ của những điểm nằm trên parabol (P) và cách đều hai trục tọa độ.
Bài 4: (1,5 điểm) Ngày 31/5/2021, Ủy ban Bầu cử của tỉnh A đã ban hành Nghị quyết
công bố 51 đại biểu là nam và nữ trúng cử Hội đồng nhân dân tỉnh khóa X, nhiệm kỳ 2021-2026.
Người ta thống kê được rằng: tuổi trung bình của các đại biểu nam trúng cử là 1612 413
tuổi; tuổi trung bình của các đại biểu nữ trúng cử là
tuổi và tuổi trung bình của 33 9 51 đạ 2438 i biểu trúng cử là
tuổi. Tính số đại biểu trúng cử là nam; số đại biểu trúng cử 51 là nữ của tỉnh A.
Bài 5: (1,0 điểm) Cho a, b là hai số thực dương sao cho a b 1
Chứng minh rằng 3a b a 3b 2 3a ba 3b
Bài 6: (3,0 điểm) Cho tam giác ABC có ba góc nhọn. Các đường cao AM, BN, CP cắt
nhau tại H. Gọi I là điểm đối xứng của H qua BC.
a) Chứng minh tứ giác ABIC nội tiếp được đường tròn (O).
b) Gọi K là trung điểm của AB, chứng minh NK là tiếp tuyến của đường tròn ngoại
tiếp của tam giác NHC.
c) Biết BN cắt đường tròn (O) tại điểm thứ hai là E và CP cắt đường tròn (O) tại điể AI BE CF
m thứ hai là F. Tính giá trị biểu thức G . AM BN CP
Bài 7: (1,0 điểm) Tất cả học sinh lớp 9 của Trường trung học cơ sở Tân Tiến tham gia
xếp hàng để đồng diễn thể dục; mỗi hàng đươc xếp không quá 25 học sinh. Nếu xếp mỗi Trang 40
hàng 16 học sinh thì còn thừa một học sinh; nếu bớt đi một hàng thì có thể chia đều tất cả
các học sinh vào các hàng còn lại sao cho số học sinh ở mỗi hàng là bằng nhau. Hỏi
Trường trung học cơ sở Tân Tiến có bao nhiêu ho5c sinh lớp 9? -----Hết----- ĐÁP ÁN
Bài 1: (1,0 điểm) a)
x x 1 x x 1 2x 4 x 2 A : x x x x x 1
x 1x x 1 x 1x x 1 2 x 2 1 x x x x : 1 1
x 1 x 1 2 x x x x x 1 1 1 2 x x 1 x 1 : . x x x 1 x 2 x 1 x 1 x 1 2
b) Với x 0; x 1 ta có: A 1 x 1 x 1
Để A nguyên thì 2 x 1 suy ra x 1 1 ;1; 2 ; 2 x 1 1 x 0 x 1 1 x 4 x 1 2 x 9 x 1 2
Với x 0; x 1, để A nguyên thì x = 4 hoặc x = 9
Bài 2: (1,0 điểm) 2 2 x x x x 2 2 2 4
3 1 x 7x 2 2
5x 20x 2 x 4x 3 0
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT THÀNH PHỐ CẦN THƠ NĂM HỌC 2021 – 2022
Khóa ngày 05 tháng 6 năm 2021 ĐỀ CHÍNH THỨC MÔN: TOÁN (CHUYÊN)
(Đề thi có 2 trang)
Thời gian làm bài: 150 phút, không kể thời gian phát đề
Câu 1. (1,5 điểm) Cho biểu thức (𝑥−1)√𝑥−1+𝑥−3 1 1 𝑃 = [ − ] : với x > 1 và x ≠ 2. 𝑥−2 √𝑥−1+1 (𝑥−1)√𝑥−1−𝑥+1 Trang 41
a) Rút gọn biểu thức P.
b) Tính giá trị của P khi 𝑥 = √7 + 4√3 − (√5 + 1)√7 − 4√3 + √5|√3 − 2|.
Câu 2. (1,5 điểm) Cho parabol (P): y = x2 và đường thẳng (d): y = –2mx – 2m. Tìm tất cả giá trị của tham
số m sao cho (d) cắt (P) tại hai điểm phân biệt có hoành độ x1 và x2 thỏa mãn |𝑥1| + |𝑥2| = 2√3.
Câu 3. (2,0 điểm) Giải phương trình và hệ phương trình sau trên tập số thực:
a) 𝑥 + 2√2𝑥 + 1 = 4√𝑥 + 2.
(𝑥 + 2)2 = 12𝑥 + 4𝑦 + 1 b) { .
(𝑦 − 1)2 = 2𝑦 + 4𝑥 + 2 Câu 4. (2,0 điểm)
a) Tìm tất cả các cặp số nguyên (x, y) thỏa mãn x2 + 5y2 + 4xy + 4y + 2x – 3 = 0.
b) Lúc 7 giờ, anh Toàn điều khiển một xe gắn máy khởi hành từ thành phố A đến thành phố B. Khi đi đượ 3
c quãng đường, xe bị hỏng nên anh Toàn dừng lại để sửa chữa. Sau 30 phút sửa xe, anh Toàn tiếp 4
tục điều khiển xe gắn máy đó đi đến thành phố B với vận tốc nhỏ hơn vận tốc ban đầu 10 km/h. Lúc 10
giờ 54 phút, anh Toàn đến thành phố B. Biết rằng quãng đường từ thành phố A đến thành phố B là 160
km và vận tốc của xe trên mỗi đoạn đường không đổi. Hỏi anh Toàn dừng xe để sửa chữa lúc mấy giờ?
Câu 5. (2,0 điểm) Cho tam giác ABC (AB > BC > AC) có ba góc nhọn và nội tiếp đường tròn (O). Vẽ
đường tròn tâm C, bán kính CB cắt đường thẳng AB tại điểm D và cắt đường tròn (O) tại điểm thứ hai là E.
a) Chứng minh đường thẳng DE vuông góc với đường thẳng AC.
b) Đường thẳng DE cắt đường tròn (O) tại điểm thứ hai là F. Các đường thẳng CO, AB cắt nhau tại
điểm H và các đường thẳng BE, CF cắt nhau tại điểm K. Chứng minh 𝐶𝐾𝐻 ̂ = 𝐶𝐵𝐻 ̂ .
c) Gọi I là giao điểm của đường thẳng AB và CE. Chứng minh IA. IB = ID. IH.
Câu 6. (1,0 điểm) Cho x, y, z là các số thực dương. Chứng minh rằng (𝑥 + 2)2 (𝑦 + 2)2 (𝑧 + 2)2 + + ≥ 12 𝑦 + 𝑧 𝑧 + 𝑥 𝑥 + 𝑦 --------HẾT--------
Câu 1. (1,5 điểm) Cho biểu thức (𝑥−1)√𝑥−1+𝑥−3 1 1 𝑃 = [ − ] :
với x > 1 và x ≠ 2. 𝑥−2 √𝑥−1+1 (𝑥−1)√𝑥−1−𝑥+1
a) Rút gọn biểu thức P.
Với x > 1 và x ≠ 2 ta có: (𝑥−1) 1 1 𝑃 = [ √𝑥−1+𝑥−3 − ] : 𝑥−2 √𝑥−1+1 (𝑥−1)√𝑥−1−𝑥+1 (𝑥−1) 1 1 𝑃 = [ √𝑥−1−1 + 1 − ] : 𝑥−2 √𝑥−1+1 (𝑥−1)√𝑥−1−𝑥+1 ( 1
𝑃 = [ √𝑥−1−1)(𝑥−1+√𝑥−1+1) + √𝑥−1 ] : 𝑥−2 √𝑥−1+1 (𝑥−1)√𝑥−1−𝑥+1 ( 1
𝑃 = [ √𝑥−1−1)(√𝑥−1+1)(𝑥+√𝑥−1) + √𝑥−1 ] : (𝑥−2)(√𝑥−1+1) √𝑥−1+1 (𝑥−1)√𝑥−1−𝑥+1 𝑥+
𝑃 = [ √𝑥−1 + √𝑥−1 ] ∙ [(𝑥 − 1)√𝑥 − 1 − 𝑥 + 1] √𝑥−1+1 √𝑥−1+1 Trang 42 𝑥+2 𝑃 =
√𝑥−1 ∙ (𝑥 − 1)(√𝑥 − 1 − 1) √𝑥−1+1 𝑥−1+2 𝑃 =
√𝑥−1+1 ∙ (𝑥 − 1)(√𝑥 − 1 − 1) √𝑥−1+1 2 (
𝑃 = √𝑥−1+1) ∙ (𝑥 − 1)(√𝑥 − 1 − 1) √𝑥−1+1
𝑃 = (√𝑥 − 1 + 1) ∙ (𝑥 − 1)(√𝑥 − 1 − 1)
P = (x – 1)(x – 2) = x2 – 3x + 2
Vậy P = x2 – 3x + 2 với x > 1 và x ≠ 2.
b) Tính giá trị của P khi 𝑥 = √7 + 4√3 − (√5 + 1)√7 − 4√3 + √5|√3 − 2|.
𝑥 = √7 + 4√3 − (√5 + 1)√7 − 4√3 + √5|√3 − 2|
𝑥 = √4 + 4√3 + 3 − (√5 + 1)√4 − 4√3 + 3 + √5(2 − √3) (do √3 < 2 ) 2 2
𝑥 = √(2 + √3) − (√5 + 1)√(2 − √3) + √5(2 − √3)
𝑥 = 2 + √3 − (√5 + 1)(2 − √3) + √5(2 − √3) (do 2 − √3 > 0 )
𝑥 = 2 + √3 − (2 − √3)(√5 + 1 − √5)
𝑥 = 2 + √3 − 2 + √3 = 2√3 (thỏa điều kiện) 2
Thay 𝑥 = 2√3 vào P ta được 𝑃 = (2√3) − 3 ∙ 2√3 + 2 = 14 − 6√3 Vậy 𝑃 = 14 − 6√3.
Câu 2. (1,5 điểm) Cho parabol (P): y = x2 và đường thẳng (d): y = –2mx – 2m. Tìm tất cả giá trị của
tham số m sao cho (d) cắt (P) tại hai điểm phân biệt có hoành độ x1 và x2 thỏa mãn |𝑥1| + |𝑥2| = 2√3 . Giải:
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình:
x2 = –2mx – 2m ⇔ x2 + 2mx + 2m = 0 (1) Ta có: ∆’ = m2 – 2m.
(d) cắt (P) tại hai điểm phân biệt có hoành độ x1 và x2
⇔ Phương trình (1) có 2 nghiệm phân biệt x1 và x2 𝑚 > 2 { 𝑚 > 2 ⇔ 𝑚 > 0
∆’ > 0 ⇔ m2 – 2m > 0 ⇔ m. (m – 2) > 0 ⇔ [ ⇔ [ 𝑚 < 2 { 𝑚 < 0 𝑚 < 0 𝑥
Theo định lý Vi-ét ta có: { 1 + 𝑥2 = −2𝑚 𝑥1 ∙ 𝑥2 = 2𝑚 Theo đề bài ta có: |𝑥1| + |𝑥2| = 2√3 ⇔ (|𝑥1| + |𝑥2|)2 = 12 ⇔ 𝑥2 2
1 + 𝑥2 + 2|𝑥1 ∙ 𝑥2| = 12
⇔ (𝑥1 + 𝑥2)2 − 2𝑥1 ∙ 𝑥2 + 2|𝑥1 ∙ 𝑥2| = 12
⇔ (−2𝑚)2 − 2 ∙ 2𝑚 + 2|2𝑚| = 12
⇔ 4𝑚2 − 4𝑚 + 4|𝑚| = 12 (*)
Với m > 2 thì (*) trở thành: 4m2 – 4m + 4m = 12 ⇔ m2 = 3 (loại vì m2 > 4) 𝑚 = −1(𝑛ℎ𝑎𝑛)
Với m < 0 thì (*) trở thành: 4m2 – 8m – 12 = 0 ⇔ m2 – 2m – 3 = 0 ⇔ [ 𝑚 = 3(𝑙𝑜𝑎𝑖) Trang 43
Vậy với m = –1 thì (d) cắt (P) tại hai điểm phân biệt có hoành độ x1 và x2 thỏa mãn đề bài.
Câu 3. (2,0 điểm) Giải phương trình và hệ phương trình sau trên tập số thực:
a) 𝑥 + 2√2𝑥 + 1 = 4√𝑥 + 2. ĐKXĐ: x ≥ 0
𝑥 + 2√2𝑥 + 1 = 4√𝑥 + 2
⇔ 2𝑥 + 1 + 2√2𝑥 + 1 + 1 = 𝑥 + 4√𝑥 + 4 2 2
⇔ (√2𝑥 + 1 + 1) = (√𝑥 + 2)
⇔ |√2𝑥 + 1 + 1| = |√𝑥 + 2|
⇔ √2𝑥 + 1 + 1 = √𝑥 + 2
(do √2𝑥 + 1 + 1 > 0 , √𝑥 + 2 > 0 )
⇔ √2𝑥 + 1 = √𝑥 + 1
⇔ 2𝑥 + 1 = 𝑥 + 1 + 2√𝑥 ⇔ 2√𝑥 = 𝑥 𝑥 = 0 ⇔ x2 – 4x = 0 ⇔ [ (thỏa điều kiện) 𝑥 = 4
Vậy phương trình có tập nghiệm S = {0; 4} (x + 2)2 = 12x + 4y + 1 b) { . (y − 1)2 = 2y + 4x + 2
𝑥2 + 4𝑥 + 4 = 12𝑥 + 4𝑦 + 1
𝑥2 − 8𝑥 − 4𝑦 + 3 = 0(1) ⇔ { ⇔ {
𝑦2 − 2𝑦 + 1 = 2𝑦 + 4𝑥 + 2
𝑦2 − 4𝑦 − 4𝑥 − 1 = 0(2) 𝑥 − 2 = 𝑦
Lấy (1) – (2) ta được: x2 – y2 – 4x + 4 = 0 ⇔ (x – 2)2 = y2 ⇔ [𝑥 − 2 = −𝑦 𝑥 = 1
TH1: y = x – 2 thay vào (1) ta được: x2 – 8x – 4(x – 2) + 3 = 0 ⇔ x2 – 12x + 11 = 0 ⇔ [ 𝑥 = 11
Với x = 1 thì y = 1 – 2 = –1
Với x = 11 thì y = 11 – 2 = 9 𝑥 = −1
TH2: –y = x – 2 thay vào (1) ta được: x2 – 8x + 4(x – 2) + 3 = 0 ⇔ x2 – 4x – 5 = 0 ⇔ [ 𝑥 = 5
Với x = –1 thì y = 2 – (–1) = 3
Với x = 5 thì y = 2 – 5 = –3
Vậy hệ phương trình có tập nghiệm: S = {(1 ; –1) ; (11 ; 9) ; (–1 ; 3) ; (5 ; –3)}
Câu 4. (2,0 điểm)
a) Tìm tất cả các cặp số nguyên (x, y) thỏa mãn x2 + 5y2 + 4xy + 4y + 2x – 3 = 0.
Ta có: x2 + 5y2 + 4xy + 4y + 2x – 3 = 0
⇔ (x2 + 4xy + 4y2) + y2 + 2(x + 2y) + 1 – 4 = 0
⇔ [(x + 2y)2 + 2(x + 2y) + 1] = 4 ⇔ (x + 2y + 1)2 + y2 = 4 (𝑥 + 2𝑦 + 1)2 = 4 { (𝐼) 𝑦2 = 0
Vì x, y ∈ ℤ nên phương trình trên tương đương với (𝑥 + 2𝑦 + 1)2 = 0 { (𝐼𝐼) [ 𝑦2 = 4 Giải (I): Trang 44 (𝑥 + 2𝑦 + 1)2 = 4 𝑥 + 1 = 2 𝑥 = 1 (𝑥 + 1)2 = 4 [ [ 𝑥 = 1 , 𝑦 = 0 { ⇔ {
⇔ { 𝑥 + 1 = −2 ⇔ { 𝑥 = −3 ⇔ [ 𝑦2 = 0 𝑦 = 0 𝑦 = 0 𝑦 = 0 𝑥 = −3 , 𝑦 = 0 Giải (II): 𝑥2𝑦 + 1 = 0 𝑥 + 2𝑦 + 1 = 0 { (𝑥 + 2𝑦 + 1)2 = 0 𝑦 = 2 𝑥 = −5 , 𝑦 = 2 { ⇔ { 𝑦 = 2 ⇔ [ ⇔ [ 𝑦2 = 4 [ 𝑥 + 2𝑦 + 1 = 0 𝑥 = 3 , 𝑦 = −2 𝑦 = −2 { 𝑦 = −2
Vậy tập nghiệm nguyên của phương trình là: S = {(1; 0); (–3; 0); (–5; 2); (3; –2)}.
b) Lúc 7 giờ, anh Toàn điều khiển một xe gắn máy khởi hành từ thành phố A đến thành phố B. Khi đi đượ 3
c quãng đường, xe bị hỏng nên anh Toàn dừng lại để sửa chữa. Sau 30 phút sửa xe, anh Toàn 4
tiếp tục điều khiển xe gắn máy đó đi đến thành phố B với vận tốc nhỏ hơn vận tốc ban đầu 10 km/h. Lúc
10 giờ 54 phút, anh Toàn đến thành phố B. Biết rằng quãng đường từ thành phố A đến thành phố B là
160 km và vận tốc của xe trên mỗi đoạn đường không đổi. Hỏi anh Toàn dừng xe để sửa chữa lúc mấy giờ? Giải:
Gọi vận tốc xe ban đầu là x (km/h) (x > 10).
Vận tốc sau khi sửa chữa xe là: x – 10 (km/h) 3
Quãng đường từ A đến đoạn đường bị hỏng xe là: ∙ 160 = 120 (km) 4
Quãng đường còn lại là: 160 – 120 = 40 (km). 120 40
Thời gian đi từ A đến đoạn đường bị hỏng xe là:
(h), thời gian đi từ lúc đã sửa xe đến B là (h) 𝑥 𝑥−10
Anh Toàn phải dừng lại sửa xe 30 phút = 0,5 h nên tổng thời gian đi từ A đến B là: 120 40 + 0.5 + (h) 𝑥 𝑥−10
Vì lúc đi từ A là 7 giờ và đi đến B là 10 giờ 54 phút nên tổng thời gian đi từ A đến B (kể cả thời gian sửa
xe là 3 giờ 54 phút = 3,9 (h) 120 40 Vậy ta có phương trình: + 0.5 + = 3,9 𝑥 𝑥−10 120 40 ⇔ + = 3,4 𝑥 𝑥−10
⇒ 120(x – 10) + 40x = 3,4x. (x – 10) ⇔ 3,4x2 – 194x + 1200 = 0 (1)
∆’ = 972 – 3,4. 1200 = 5329 = 732 > 0 nên phương trình (1) có 2 nghiệm phân biệt: x1 = 50 (thỏa đk) 120 𝑥2 = < 10 (không thỏa đk) 17
Suy ra vận tốc của xe đi từ A đến lúc bị hỏng xe là 50 km/h 120
Thời gian anh Toàn đi từ A đến lúc bị hỏng xe là = 2,4 (h) 50
Vậy anh Toàn dừng xe để sửa chữa lúc: 7 + 2,4 = 9,4 (h) = 9 giờ 24 phút
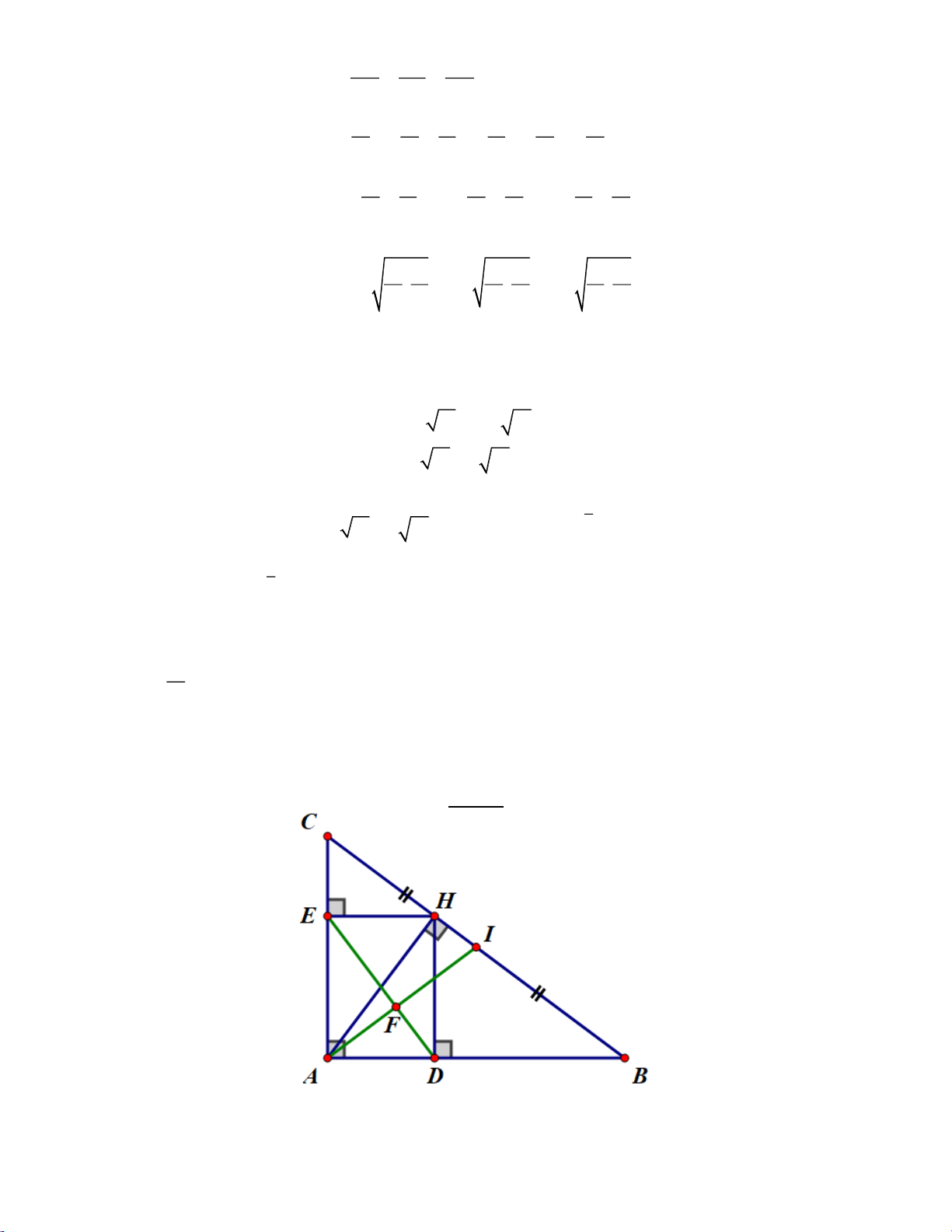
Câu 5. (2,0 điểm) Cho tam giác ABC (AB > BC > AC) có ba góc nhọn và nội tiếp đường tròn (O). Vẽ
đường tròn tâm C, bán kính CB cắt đường thẳng AB tại điểm D và cắt đường tròn (O) tại điểm thứ hai là E.
a) Chứng minh đường thẳng DE vuông góc với đường thẳng AC. Trang 45 Xét (O): 𝐴𝐸𝐶 ̂ = 𝐴𝐵𝐶
̂ (2 góc nôi tiếp chắn cung AC)
∆CBD có CB = CD (bán kính (C)) ⇒∆CBD cân tại C ⇒ 𝐶𝐵𝐷 ̂ = 𝐶𝐷𝐵 ̂ Suy ra 𝐶𝐸𝐴 ̂ = 𝐶𝐷𝐵 ̂ Mà ta có: 𝐶𝐸𝐷 ̂ = 𝐶𝐸𝐴 ̂ + 𝐴𝐸𝐷 ̂ 𝐶𝐷𝐸 ̂ = 𝐶𝐷𝐵 ̂ + 𝐴𝐷𝐸 ̂
∆CED có CE = CD (bán kính (C)) ⇒∆CED cân tại C ⇒ 𝐶𝐸𝐷 ̂ = 𝐶𝐷𝐸 ̂ Suy ra: 𝐴𝐸𝐷 ̂ = 𝐴𝐷𝐸
̂ nên ∆ADE cân tại A ⇒ AE = AD
Ta lại có: CE = CD (bán kính (C)) nên AC là trung trực của ED Suy ra AC ⊥ ED
b) Đường thẳng DE cắt đường tròn (O) tại điểm thứ hai là F. Các đường thẳng CO, AB cắt nhau tại
điểm H và các đường thẳng BE, CF cắt nhau tại điểm K. Chứng minh rằng: 𝐶𝐾𝐻 ̂ = 𝐶𝐵𝐻 ̂ . *Ta có: 𝐹𝐵𝐷 ̂ = 𝐴𝐸𝐷
̂ (𝑔ó𝑐 𝑡𝑟𝑜𝑛𝑔 𝑏ằ𝑛𝑔 𝑔ó𝑐 𝑛𝑔𝑜à𝑖 đố𝑖 𝑑𝑖ệ𝑛 𝑐ủ𝑎 𝑡ứ 𝑔𝑖á𝑐 𝑛ộ𝑖 𝑡𝑖ế𝑝 𝐵𝐶𝐸𝐹) Mà 𝐹𝐵𝐷 ̂ = 𝐹𝐶𝐴
̂ (2 góc nội tiếp chắn cung FA của (O)) Và 𝐴𝐸𝐷 ̂ = 𝐴𝐷𝐸 ̂ (chứng minh câu a) Nên 𝐹𝐵𝐷 ̂ = 𝐴𝐷𝐸 ̂ hay 𝐹𝐵𝐷 ̂ = 𝐵𝐷𝐹 ̂
Do đó ∆FBD cân tại F ⇒ FB = FD Mà CB = CD (bán kính (C))
Nên FC là trung trực của BD ⇒ FC ⊥ DB hay BH ⊥CK
*Ta có: CE = CB (bán kính (C)) và OE = OB (bán kính (O))
Suy ra OC là trung trực của BE ⇒ OC ⊥BE hay CH ⊥BK Xét ∆BCK: CH ⊥BK (cmt) BH ⊥CK (cmt)
Suy ra H là trực tâm ∆BCK nên KH ⊥BC ⇒ 𝐶𝐾𝐻 ̂ + 𝐾𝐶𝐵 ̂ = 900
Mà BH ⊥CK (cmt) ⇒ 𝐶𝐵𝐻 ̂ + 𝐾𝐶𝐵 ̂ = 900 Nên 𝐶𝐾𝐻 ̂ = 𝐶𝐵𝐻 ̂ (đpcm) Trang 46
c) Gọi I là giao điểm của đường thẳng AB và CE. Chứng minh IA. IB = ID. IH. *Xét ∆IAE và ∆IBC có: 𝐴𝐸𝐼 ̂ = 𝐶𝐵𝐼
̂ (2 góc nội tiếp chắn cung AC của (O)) 𝐸𝐼𝐴 ̂ = 𝐵𝐼𝐶 ̂ (2 góc đối đỉnh) 𝐼𝐸 𝐼𝐴
⇒ ∆IAE ∽ ∆ICB (g – g) ⇒ = 𝐼𝐵 𝐼𝐶 ⇒IE. IC = IB. IA
* Ta có: B đối xứng E qua CO (OC là trung trực của BE) ⇒ 𝐶𝐵𝐻 ̂ = 𝐶𝐸𝐻
̂ (tính chất đối xứng) Và: 𝐶𝐵𝐻 ̂ = 𝐶𝐷𝐻 ̂ (∆CBD cân tại C) Nên: 𝐶𝐸𝐻 ̂ = 𝐶𝐷𝐻 ̂
⇒ CDEH nội tiếp (2 đỉnh kề nhau E, D cùng nhìn cạnh CH dưới các góc bằng nhau) ⇒ 𝐷𝐸 ̂ 𝐼 = 𝐶𝐻𝐼 ̂ Xét ∆IED và ∆IHC có: 𝐷𝐸𝐼 ̂ = 𝐶𝐻𝐼 ̂ (cmt) 𝐸𝐼𝐷 ̂ = 𝐻𝐼𝐶 ̂ (2 góc đối đỉnh) 𝐼𝐸 𝐼𝐻
⇒ ∆IED ∽ ∆IHC (g – g) ⇒ = 𝐼𝐷 𝐼𝐶 ⇒IE. IC = ID. IH Mà IE. IC = IB. IA (cmt) Vậy IB. IA = ID. IH (đpcm)
Câu 6. (1,0 điểm) Cho x, y, z là các số thực dương. Chứng minh rằng (𝑥+2)2 (𝑦+2)2 (𝑧+2)2 + + ≥ 12 𝑦+𝑧 𝑧+𝑥 𝑥+𝑦 𝑥2 𝑦2 𝑧2 (𝑥+𝑦+𝑧)2 𝑥 𝑦 𝑧
Áp dụng Bất dẳng thức phụ + + ≥
. Dấu “=” xảy ra khi = = , a, b, c > 0 𝑎 𝑏 𝑐 𝑎+𝑏+𝑐 𝑎 𝑏 𝑐
Chứng minh BĐT phụ: 𝑥 𝑦 𝑐
Áp dụng BĐT B.C.S cho hai bộ số ( ; ;
) và (√𝑎; √𝑏; √𝑐) ta có: √𝑎 √𝑏 √𝑐 𝑥2 𝑦2 𝑧2 𝑥2 𝑦2 𝑧2 (𝑥+𝑦+𝑧)2 ( + +
) (𝑎 + 𝑏 + 𝑐) ≥ (𝑥 + 𝑦 + 𝑧)2 ⇔ + + ≥ 𝑎 𝑏 𝑐 𝑎 𝑏 𝑐 𝑎+𝑏+𝑐 Khi đó ta có: (𝑥+2)2 (𝑦+2)2 (𝑧+2)2 (𝑥+𝑦+𝑧+6)2 + + ≥ 𝑦+𝑧 𝑧+𝑥 𝑥+𝑦 2(𝑥+𝑦+𝑧) (𝑥+2)2 (𝑦+2)2 (𝑧+2)2
(𝑥+𝑦+𝑧)2+12(𝑥+𝑦+𝑧)+36 ⇒ + + ≥ 𝑦+𝑧 𝑧+𝑥 𝑥+𝑦 2(𝑥+𝑦+𝑧) (𝑥+2)2 (𝑦+2)2 (𝑧+2)2 𝑥+𝑦+𝑧 18 ⇒ + + ≥ + + 6 𝑦+𝑧 𝑧+𝑥 𝑥+𝑦 2 𝑥+𝑦+𝑧 (𝑥+2)2 (𝑦+2)2 (𝑧+2)2 𝑥+𝑦+𝑧 18 ⇒ + + ≥ 2√ ∙ + 6 (BĐT 𝑦+𝑧 𝑧+𝑥 𝑥+𝑦 2 𝑥+𝑦+𝑧 Cauchy) (𝑥+2)2 (𝑦+2)2 (𝑧+2)2 ⇒ + + ≥ 2√9 + 6 = 12 𝑦+𝑧 𝑧+𝑥 𝑥+𝑦 𝑥+2 𝑦+2 𝑧+2 = = 𝑦+𝑧 𝑧+𝑥 𝑥+𝑦
Dấu “=” xảy ra khi và chỉ khi { 𝑥+𝑦+𝑧 18 ⇔ = 2 𝑥+𝑦+𝑧 𝑥 = 𝑦 = 𝑧
{(𝑥 + 𝑦 + 𝑧)2 = 36 ⇔ x = y = z = 2 Trang 47
ĐỀ THI VÀO 10 CHUYÊN TOÁN - THPT CHUYÊN NGUYỄN DU – 2021 – 2022
Câu 1. Cho phương trình 4
x m 2
2 x 3m 3 0 với m là tham số. Tìm tất cả giá trị của m
để phương trình đã cho có bốn nghiệm phân biệt x , x , x , x sao cho 1 2 3 4 4 4 4 4
x x x x 2x x x x đạt giá trị nhỏ nhất. 1 2 3 4 1 2 3 4 Câu 2.
1) Giải phương trình 2022 2022x 2021 2023x 2022 2023 3 3
x 6xy y 8
2) Giải hệ phương trình 2
2x y 3 5x y 3 x y 5 Câu 3.
1) Tìm tất cả các số tự nhiên n và k để 4 2 1 4 k n là số nguyên tố.
2) Tìm tất cả các số nguyên dương , x y thỏa mãn 4 2 2 2
x x 2x y 2xy 2 y 2 y 36 0
Câu 4. Cho ba số thực dương a, b, c thỏa mãn a b c 2 . Tìm giá trị nhỏ nhất của biểu thức: b a 2 1 c b 2 1 a c 2 2 2 2 1 P . 2 a 2 b 2 1 b 2 c 2 1 c 2 a 1
Câu 5. Cho nửa đường tròn ;
O R đường kính AB . Lấy điểm C tùy ý trên nửa đường tròn đó (
C khác A và B ). Gọi M , N lần lượt là điểm chính giữa của cung AC và cung BC . Hai đường
thẳng AC và BN cắt nhau tại D . Hai dây cung AN và BC cắt nhau tại H .
1) Chứng minh tứ giác CDNH nội tiếp.
2) Gọi I là trung điểm DH . Chứng minh IN là tiếp tuyến của nửa đường tròn ; O R .
3) Chứng minh rằng khi C di động trên nửa đường tròn ;
O R thì đường thẳng MN luôn
tiếp xúc với một đường tròn cố định.
4) Trên nửa đường tròn ;
O R không chứa C lấy một điểm P tùy ý ( P khác A và B ). Gọi
Q, R, S lần lượt là hình chiếu vuông góc của P trên AB, BC, CA . Tìm vị trí của P để tổng AB BC CA
đạt giá trị nhỏ nhất. PQ PR PS Trang 48
Câu 1. Cho phương trình 4
x m 2
2 x 3m 3 0 với m là tham số. Tìm tất cả giá trị của m
để phương trình đã cho có bốn nghiệm phân biệt x , x , x , x sao cho 1 2 3 4 4 4 4 4
x x x x 2x x x x đạt giá trị nhỏ nhất. 1 2 3 4 1 2 3 4 Lời giải Đặt 2
x t , t 0 . Phương trình trở thành: 2
t m 2t 3m 3 0 1
Phương trình đã cho có bốn nghiệm phân biệt khi phương trình 1 có hai nghiệm dương
phân biệt 0 t t . 1 2
m 22 43m 3 0 2
m 8m 16 0 m 1
Ta được S m 2 0 m 1 m 4
P 3m 3 0
Giả sử x x x x 1 2 3 4 Khi đó, đặt 2 2 x x t ; 2 2 x
x t ; t 0;t 0 . 1 4 2 2 3 1 1 2 Ta có 2
P 2t 2t
2t t 2S 6P 2m 22 5 27 27 2 2 2 63m 3 2
2m 10m 26 2 m 1 2 1 2 2 2 2 5
Dấu bằng xảy ra khi m (thỏa mãn điều kiện) 2 27 5
Vậy giá trị nhỏ nhất của P là , đạt khi m . 2 2 Câu 2.
1) Giải phương trình 2022 2022x 2021 2023x 2022 2023 3 3
x 6xy y 8
2) Giải hệ phương trình 2
2x y 3 5x y 3 x y 5 Lời giải 2021 x 2022 2022 1) Điều kiện: x 2022 2023 x 2023
2022 2022x 2021 2023x 2022 2023
2022 2022x 2021
1 2023x 2022 1 0
2022 2022x 2022 2023x 2023 0 2022x 2021 1 2023x 2022 1 x 2 2022 2023 1 0 2022x 2021 1 2023x 2022 1 x 1
Vậy phương trình có nghiệm duy nhất x 1 2) 3 3
x 6xy y 8 Trang 49
x y3 3xy x y 6xy 8 0
x y 2 x y2 2x y 4 3xy x y 2 0
x y 2 2 2
x 2xy y 2x 2 y 4 3xy 0
x y 2 2 2
x y xy 2x 2 y 4 0
y x 2
x y 2 0 x 2 y x x 2 2
2 y 22 x y2 0 y 2 x y Thay vào phương trình 2
2x y 3 5x y 3 x y 5, ta được 1 2
3x 1 4x 5 x x 7 DK : x 3
3x 1 2 4x 5 3 2x x 2 0 x 3 4 1 x 2 0 3x 1 2 4x 5 3 x 1 Vậy hệ có nghiệm ; x y 1; 1 . Câu 3.
1) Tìm tất cả các số tự nhiên n và k để 4 2 1 4 k n là số nguyên tố.
2) Tìm tất cả các số nguyên dương , x y thỏa mãn 4 2 2 2
x x 2x y 2xy 2 y 2 y 36 0 Lời giải
A n 4 k n 2 2 k 2 n 2 k 2 4 2 1 2 2 1 2 2 1 2 2k 1 2n .2
n 2 k 2 .n2k 2 2 2 1 1 2 2k 1 k 1 n 2 . n 2 2 2k 1 k 1 n 2 . n 2 2 k 1 2 k 1
A là số nguyên tố 2 2k 1 k 1 n 2 .2 n 1 2 n 2. . n 2 2 n 2 n 1 n 1 k n 2 1 2 2 n 2 k 1 n 2 1 k 0
Thử lại A 1 4 5 , thỏa mãn yêu cầu. 2) 4 2 2 2
x x 2x y 2xy 2 y 2 y 36 0 4 2 2 2
x y x y x y 2 2 1 2 2 2
x 2xy y 36 1
x y 2 x y2 2 1 37 1 2
x y 1 x y Nhận xét: x *; y * . 2
x y 1 0 Trang 50 2 2
x y 1 6
x x 4 0
x y 1
y x 1 2 2
x y 1 6
x x 6 0 x 2 1 x y 1
y x 1 y 3 2 2
x y 1 1
x x 4 0
x y 6
y x 6
Vậy phương trình có nghiệm: ; x y 2;3
Câu 4. Cho ba số thực dương a, b, c thỏa mãn a b c 2 . Tìm giá trị nhỏ nhất của biểu thức: b a 2 1 c b 2 1 a c 2 2 2 2 1 P . 2 a 2 b 2 1 b 2 c 2 1 c 2 a 1 Lời giải 3 2 Ta có 3
2 a b c 3 abc abc 3
2a 1 2b 1 2c 1 3 P 3 abc 1 a 1 1 13 a 4. 9. 13 4 9 5 a 4 9a 4 .9 a 1 b 1 1 13 b 4. 9. 13 4 9 5 b 4 9b 4 .9 b 1 c 1 1 13 c 4. 9. 13 4 9 5 c 4 9c 4 .9 c 1 1 13 3 3 13 P 3 13 . 39 12 27 5 5 5 15
4 .9 .a .b .c 3 13 2 2 24 54 2 .3 . 3 2
Dấu bằng xảy ra khi a b c 3
Câu 5. Cho nửa đường tròn ;
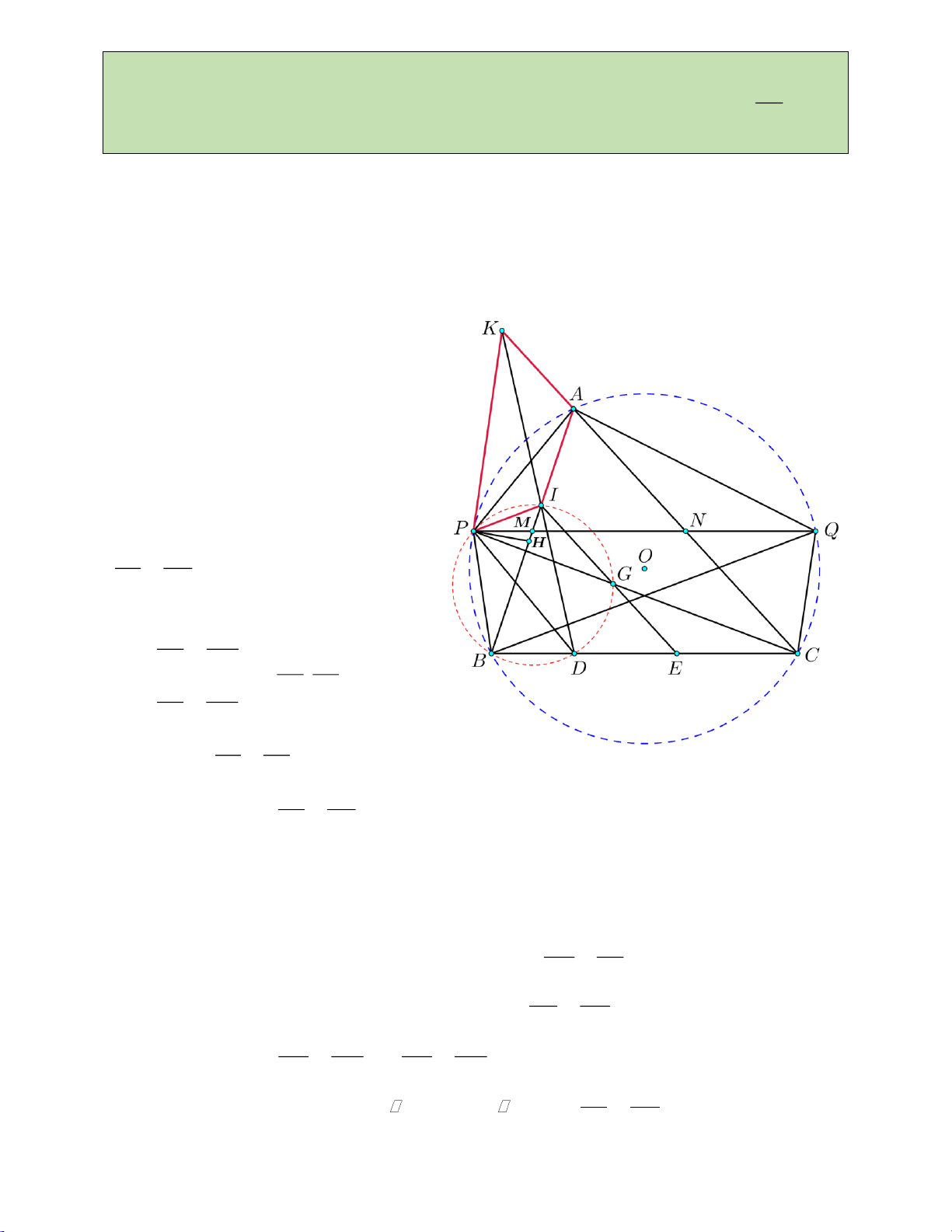
O R đường kính AB . Lấy điểm C tùy ý trên nửa đường tròn đó (
C khác A và B ). Gọi M , N lần lượt là điểm chính giữa của cung AC và cung BC . Hai đường
thẳng AC và BN cắt nhau tại D . Hai dây cung AN và BC cắt nhau tại H .
1) Chứng minh tứ giác CDNH nội tiếp.
2) Gọi I là trung điểm DH . Chứng minh IN là tiếp tuyến của nửa đường tròn ; O R .
3) Chứng minh rằng khi C di động trên nửa đường tròn ;
O R thì đường thẳng MN luôn
tiếp xúc với một đường tròn cố định. Trang 51
4) Trên nửa đường tròn ;
O R không chứa C lấy một điểm P tùy ý ( P khác A và B ). Gọi
Q, R, S lần lượt là hình chiếu vuông góc của P trên AB, BC, CA . Tìm vị trí của P để tổng AB BC CA
đạt giá trị nhỏ nhất. PQ PR PS Lời giải
1) Có AC CH DCH 90 ; AN NB HND 90
DCH DNH 180 tứ giác CDNH là tứ giác nội tiếp.
2) Tam giác DNH vuông tại N có NI là trung tuyến ứng với cạnh huyền. Ta được INH IHN .
Tứ giác CDNH nội tiếp nên IHN NCD
Tứ giác ACNB nội tiếp nên NCD NBA
Tam giác ONB cân tại O nên NBA ONB NBA ONA 90
Suy ra INO 90 . Vậy IN là tiếp tuyến của nửa đường tròn ; O R .
3) Ta có OM là tia phân giác góc AOC , ON là tia phân giác góc NOB . Hai góc này kề bù,
suy ra ON OM .
Tam giác OMN vuông cân tại O . Gọi J là trung điểm MN , ta có MN OJ ; 1 1 R 2 2 2 OJ MN R R 2 2 2 R 2
Suy ra MN luôn tiếp xúc với đường tròn tâm O , bán kính . 2 4) 2 2 2 AB BC CA P P . Q AB P . R BC PS.CA Có P . Q AB P . A PB BC P . R BC P .
B PC.sin BPC P .
B PC.sin BAC P . B PC. AB AC
PS.CA P .
A PC.sin APC P .
A PC.sin APC P .
A PC.sin ABC P . A PC. AB Trang 52 2 2 Ta đượ AB A . B AC A . B BC AB A . B AC.PA A . B BC.PB c P P . A PB PC.PB PC.PA P . A PB P . A P . B PC 2 AB
AB AC PA BC PB 2 . . AB A . B A . B PC
d / l Ptolemy P . A PB P . A P . B PC P . A PB P . A P . B PC 2 2 AB 4AB 2 4 2 2 P . A PB PA PB
Dấu bằng xảy ra khi P là điểm chính giữa cung AB không chứa C . Trang 53



