



















Preview text:
ĐỀ 1
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
PHẦN I. TRẮC NGHIỆM (3,0 điểm)
Câu 1: Đồ thị của hàm số y = (m- ) 2
1 x đi qua điểm A(- 1; ) 4 khi A. m 1. B. m 2. C. m 4. D. m 5.
Câu 2: Tích các nghiệm của phương trình 2
4x 5x 1 0 bằng 1 5 A. 1. B. . C. . D. 0. 4 4
x y m 1
Câu 3: Hệ phương trình
có nghiệm x ; y thỏa mãn 2
x y thì giá trị của m là 0 0
x y m 3 0 0 A. m 4. B. m 3. C. m 2. D. m 1.
Câu 4: Giá trị nào của x dưới đây là nghiệm của phương trình 2
x 3x 2 0 ? A. x 1. B. x 2. C. x 3. D. x 1.
Câu 5: Cho tam giác ABC đều có chu vi bằng 18cm nội tiếp đường tròn ( ; O ) R . Tính R. A. R 3 cm.
B. R 3 3 cm. C. R 3cm.
D. R 2 3 cm.
Câu 6: Tổng các nghiệm của phương trình 4 2
3x - x - 6 = 0 là A. 1 B. 2 C. 0 D. 2 ìï x+ y = 5 ï
Câu 7: Hệ phương trình í có nghiệm duy nhất ( , x ) y là ï 2x- y = 1 ïî A. 3; 2. B. 1; 4. C. 4 ;1 . D. 2;3.
Câu 8: Giá trị của m để phương trình: 2
x 2x m 0 ( m là tham số) có nghiệm kép là 1 1 A. m 1. B. m 1. C. m . D. m . 4 4
Câu 9: Lúc 8 giờ, kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là A. 0 120 . B. 0 80 . C. 0 240 . D. 0 40 .
Câu 10: Cho hàm số y f x 2 3
x . Khẳng định nào sau đây đúng? A. f 4 f 2 .
B. f 3 f 2. C. f 1 f 0. D. f 1 f 1 . Câu 11: Cặp số ( , x y)= (1; )
2 là nghiệm của hệ phương trình nào sau đây? ìï x + y = 3 ï ìï 2x- 3y = 1 ï ìï y = x + 1 ï ìï 2x- y = 0 ï A. í B. í C. í D. í ï 2x- y = 1 ïî ï y - x = 1 ïî ï 2x + y = 4 ïî ï x - y = 1 ïî
Câu 12: Phương trình 2
x - 3x + m= 0 có hai nghiệm x , x
(x < x ) thỏa mãn x - x = 5 khi 1 2 1 2 2 1 A. m 5 B. m 4 C. m 4 D. m 5
Câu 13: Trên đường tròn ;
O R lấy hai điểm , A B sao cho 0
AOB 45 . Độ dài cung nhỏ AB bằng R 2 R R A. B. 4 . R C. D. 4 4 2
Câu 14: Cho tam giác ABC cân tại A nội tiếp đường tròn ; O R . Biết 0
ABC 50 , số đo cung nhỏ BC là A. 0 80 . B. 0 160 . C. 0 100 . D. 0 50 . ax y 1
Câu 15: Khi hệ phương trình có nghiệm ;
x y 1;
1 thì giá trị của biểu thức 2 2 a b
x by 2 bằng Trang 1 A. 4. B. 3. C. 5. D. 6.
PHẦN II. TỰ LUẬN (7,0 điểm)
Câu 1 (1,0 điểm).
2x 3y 1
Giải hệ phương trình
x 3y 5
Câu 2 (2,0 điểm). Cho phương trình 2
x 2x 3m 1 0 1 , m là tham số.
a) Giải phương trình (1) khi 1 m . 3
b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm x , x 1 2 thỏa mãn:
x 2 x 2 4. 1 2
Câu 3 (1,5 điểm). Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Hưởng ứng lời kêu gọi toàn dân tham gia ủng hộ phòng chống dịch COVID-19, cùng chung tay
đẩy lùi dịch bệnh. Một xưởng may có 67 công nhân của tổ I và tổ II đã may được 3000 chiếc khẩu
trang để phát miễn phí cho người dân. Biết mỗi công nhân của tổ I may được 50 chiếc khẩu trang,
mỗi công nhân của tổ II may được 40 chiếc khẩu trang. Hỏi mỗi tổ có bao nhiêu công nhân?
Câu 4 (2,0 điểm). Cho đường tròn ;
O R và đường thẳng d không có điểm chung với đường tròn O. Từ điểm
A bất kì trên đường thẳng d kẻ tiếp tuyến ,
AB AC với đường tròn O ( ,
B C là tiếp điểm). Từ O
kẻ OH vuông góc với đường thẳng d tại .
H Dây BC cắt OA tại D và cắt OH tại . E Chứng minh rằng:
a) Tứ giác ABOC là tứ giác nội tiếp. b) OA ^ BC . c) 2
OE.OH = R .
Câu 5 (0,5 điểm).
Tìm tất cả các giá trị của tham số m để phương trình 3 2
x 5x m 6 x 2m 0 có ba nghiệm dương phân biệt.
-------------------------------Hết--------------------------------
Họ và tên học sinh: ............................................. Số báo danh:........................................................... ĐÁP ÁN
PHẦN I. TRẮC NGHIỆM (3,0 điểm) Mỗi ý đúng được 0,2 điểm 1 D 6 C 11 C 2 B 7 D 12 B 3 B 8 A 13 A 4 D 9 A 14 B 5 D 10 A 15 C
PHẦN II. TỰ LUẬN (7,0 điểm) Câu
Hướng dẫn, tóm tắt lời giải Điểm Câu 1 (1,0điểm)
2x 3y 1 3 x 6 Ta có 0,5
x 3y 5
x 3y 5 (1,0 x 2 x 2 điểm) 0,25
x 3y 5 y 1
Vậy hệ phương trình có nghiệm ( ; x y) (2;1) . 0,25 Câu 2 (2,0điểm) Trang 2 Với 1 m
, phương trình (1) trở thành 2 x 2x 0. 0,25 3 a) (1,0
Giải ra được x 0, x 2. 0,5 điểm) Vậy với 1 m
phương trình có tập nghiệm là {0; } 2 . 0,25 3 Phương trình ( )
1 có hai nghiệm x , x ' 0 1 2 0,25
2 m 2 1 3
1 0 2 3m 0 m 2 3 Theo bài ra ta có
x 2 x 2 4 1 2 0,25
x x 2 x x 0 (*) 1 2 1 2 b) (1,0điểm) 2
Với điều kiện m 3 ìï x + x = 2 1 2 ï 0,25
Áp dụng định lí Viet, ta có íï x x = 3m- 1 ïî 1 2 * 3m1 2.2 0 m 1 ( thỏa mãn ) Kết luận 0,25 Câu 3 (1,5điểm)
Gọi số công nhân của tổ I và tổ II lần lượt là , x y (công nhân), * , x y ; , x y 67 . 0,25
Vì cả hai tổ có 67 công nhân nên ta có phương trình x y 67 1 0,25
Số khẩu trang tổ I và tổ II may được lần lượt là 50x và 40y (chiếc) Theo đầu bài, ta có 0,25
: 50x 40y 3000 2 (1,5 điểm)
x y 67 Đưa ra hệ . 50
x 40y 3000 0,5 x 32
Giải hệ được nghiệm y 35
Kiểm tra điều kiện và kết luận 0,25 Câu 4 (2,0điểm) Trang 3 a) (0,75 điểm) H B E O A D d C Chỉ ra được 0 ABO 90 , 0 ACO 90 0,25 Tứ giác ABOC có 0 0 0
ACO ABO 90 90 180 0,25
Mà đây là hai góc đối nhau nên tứ giác ABOC nội tiếp được trong một đường tròn. 0,25 Ta có , B C ;
O R OB OC R O
BC cân tại O . 0,25 b) (0,75
Chỉ ra được tia OA là tia phân giác của BOC 0,25 điểm)
Từ đó suy ra được OA^ BC 0,25
Chứng minh được DODE đồng dạng với DOHA. c) 0,25 Suy ra O . E OH = O . D OA (0,5 điểm)
DABO vuông tại B , đường cao BD có 2 OB = O . D OA 0,25 Suy ra đpcm Câu 5 (0,5điểm) 3 2
x 5x m 6 x 2m 0 1 x 2 2
x 3x m 0 x 2 0,25 2
x 3x m 0 2 Suy ra phương trình ( )
1 luôn có một nghiệm dương là x 2 . (0,5 điểm) Phương trình
1 có ba nghiệm dương phân biệt Û phương trình ( ) 2 có hai ìï D = 9- 4m> 0 ïï ìï 9 2
ïï 2 - 3.2+ m¹ 0 ï 0< m
nghiệm dương phân biệt khác 2 < ï ï Û í Û í 4 0,25 ï 3> 0 ï ï ï ï ï m¹ 2 î ïï m> 0 ïî Kết luận Tổng 7,0 điểm Trang 4 ĐỀ 2
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
I- TRẮC NGHIỆM (6,0 điểm): Chọn đáp án đúng và ghi vào bảng trắc nghiệm phần bài làm 2x y 1
Câu 1: Cặp số nào sau đây là nghiệm của hệ phương trình: ? x y 2
A. (-1; -3) B. (-1; 3) C. (2; 0) D. (-2; 4)
y (2 a)x 1
Câu 2: Với giá trị nào của a thì hệ phương trình : vô nghiệm ?
y ax 3 A. a = 0 B. a = 1 C. a = 2 D. a = 3
Câu 3: Hệ phương trình nào sau đây có nghiệm duy nhất ? 3
x y 3 3
x y 3 3
x y 3
3x y 3 A. B. C. D. 3
x y 1 3
x y 1 3
x y 1
6x 2y 6
Câu 4: Hai kệ sách có 400 cuốn. Nếu chuyển từ kệ thứ nhất sang kệ thứ hai 10 cuốn thì số sách ở
kệ thứ hai bằng số sách ở kệ thứ nhất. Số sách lúc đầu ở kệ thứ nhất và kệ thứ hai lần lượt bằng:
A. 190 cuốn; 210 cuốn. B. 210 cuốn; 190 cuốn.
C. 200 cuốn; 200 cuốn. D. 100 cuốn; 300 cuốn.
Câu 5: Hàm số y = -2x2 đồng biến khi: A. x> 0 B. x > -1 C. x < 0 D. x < 1 Câu 6: Điểm 1 1 M ;
thuộc đồ thị hàm số nào: 4 16 1 A. 2 y x B. 2 y x C. 2 y 5x D. 2 y x 5
Câu 7: Phương trình nào sau đây là phương trình bậc hai một ẩn ? A. 2 5
x 2x 1 0 B. 3
2x x 5 0 C. 2
4x xy 5 0 D. 2
0x 3x 1 0
Câu 8: Cho phương trình : 2
ax bx c 0a 0 . Nếu 2
b 4ac 0 thì phương trình có nghiệm là: a b c 1 b
A. x x x x x x
x x . 1 2 B. 1 2 C. 1 2 D. 1 2 2b a a 2 a
Câu 9: Số nghiệm của phương trình : 4 2
x 3x 2 0 là: A. 2 B. 3 C. 1 D. 4
Câu 10: Phương trình x2 - 3x - 4 = 0 có số nghiệm là:
A. 1 B. 2 C. 3 D. 4
Câu 11: Gọi S và P lần lượt là tổng và tích hai nghiệm của phương trình: 2
x 5x 10 0 . Khi đó S + P bằng: A. -15 B. -10 C. -5 D. 5
Câu 12: Hai số 6 và 4 là nghiệm của phương trình nào?
A. x2 - 10x + 24 = 0 B. x2 - 24x + 10 = 0 C. x2 - 6x + 4 = 0 D. x2 + 10x +24 = 0
Câu 13: Nếu x ; x là 2 nghiệm của phương trình 2
2x 3x 5 0 thì biểu thức 2 2
x x có giá trị là: 1 2 1 2 29 29 25 A. B. 29 C. D. 2 4 4
Câu 14: Cho đường tròn (O) và góc nội tiếp 0
BAC 130 . Số đo của góc BOC là: Trang 5 A. 1300 B. 1000 C. 2600 D. 500
Câu 15: Cho ABC nội tiếp đường tròn tâm O. Biết 0 A 50 ; 0
B 65 . Kẻ OH AB; OI AC;
OK BC. So sánh OH, OI, OK ta có: A. OH = OI = OK B. OH = OI > OK C. OH = OI < OK D. OH > OI > OK
Câu 16: Trong hình bên M A Biết: 0 APB 40 ; 0 MBN 70 . P O
Số đo của cung nhỏ AB bằng: A. 1000 B. 900 B N C. 600 D. 700
Câu 17: Số đo góc có đỉnh bên ngoài đường tròn bằng ..................số đo hai cung bị chắn A. nửa hiệu B. tổng C. hiệu D. nửa tổng
Câu 18: Tứ giác ABCD nội tiếp đường tròn có A = 400 ; B = 600 . Khi đó C + D bằng: A. 200 B . 300 C . 1200 D . 2600
Câu 19. Độ dài cung tròn 1200 của đường tròn có bán kính 3 cm là: A. cm B . 2 cm C . 3 cm D . 4 cm
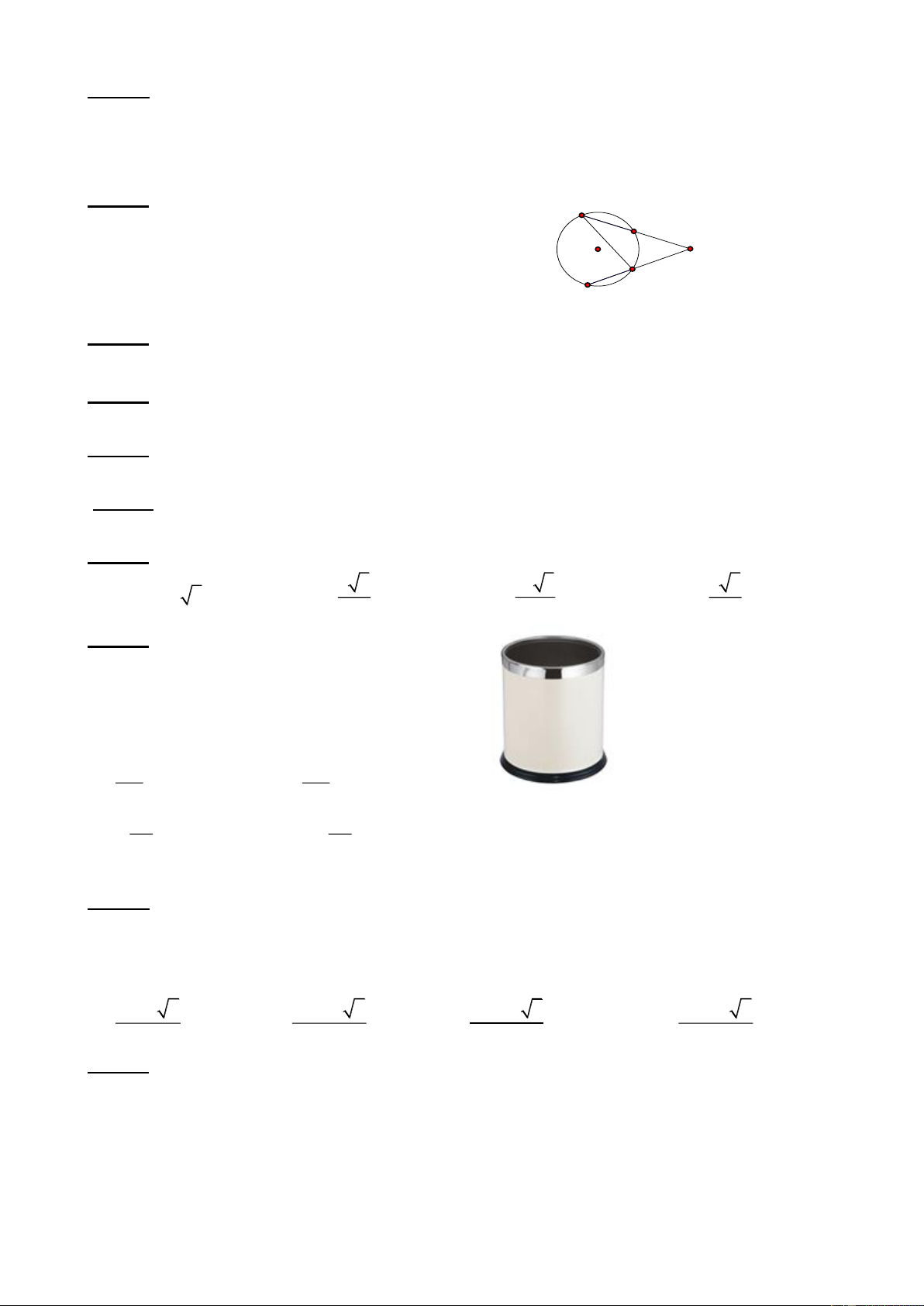
Câu 20 Độ dài cung AB của đường tròn (O;5cm) là 20 cm. Diện tích hình quạt tròn AOB là: A. 500 cm2 B. 100 cm2 C. 50 cm2 D. 20 cm2
Câu 21: Tam giác đều ABC có cạnh 10cm nội tiếp trong đường tròn (O;R), khi đó R bằng: 5 3 10 3 5 3 A. 5 3 cm B. cm C. cm D. cm 3 3 2
Câu 22: Hiện nay các văn phòng thường sử
dụng loại thùng rác văn phòng, màu sắc, chất
liệu thân thiện với môi trường. Hình ảnh bên là
một thùng rác văn phòng có chiều cao 0,8 m,
đường kính 0,4 m. Thể tích của thùng rác bằng: 4 2 A. 3 (m ) B. 3 (m ) 125 125 4 2 C. 3 (m ) D. 3 (m ) 25 25
Câu 23: Nón là dùng để che nắng, mưa, làm quạt khi nóng. Ngày nay nón lá cũng được xem là
món quà đặc biệt cho du khách khi đến tham quan Việt Nam.
Biết một nón lá có đường kính vành là 50 cm, đường sinh của nón là 35 cm. Thể tích của một nón lá là: 625 6 6250 6 6250 3 6250 6 A. 3 (cm ) B. 3 (cm ) C. 3 (cm ) D. 3 (cm ) 3 3 3 2
Câu 24: Một hình cầu có thể tích bằng 972 cm3 thì bán kính của nó bằng: A. 9 cm B. 18 cm C. 27 cm D. 36 cm Trang 6
II- TỰ LUẬN (4,0 điểm) Bài 1: (1,0 điểm) x y 6
1/ Giải hệ phương trình: .
2x y 3
2/ Không giải phương trình, hãy tính tổng và tích hai nghiệm của phương trình sau: x2 – 7x + 12 = 0.
Bài 2: (1,0 điểm) Giải bài toán sau bằng cách lập hệ phương trình hoặc phương trình:
Máy thở là một thiết bị công nghệ hữu ích, có tác dụng hỗ trợ hô hấp cho những người rất
kém hoặc không còn khả năng tự hô hấp. Đây là thiết bị sống còn giúp chống chọi với bệnh
COVID-19 của các bệnh nhân đã mắc ở thể nặng. Theo ước tính có khoảng 10% bệnh nhân mắc
bệnh COVID-19 phải dùng đến máy thở, do đó khi dịch bệnh bùng phát thì trên thế giới sẽ thiếu
hụt nghiêm trọng các thiết bị này.
Để chủ động ứng phó dịch bệnh, một nhà máy được giao sản xuất 360 chiếc máy thở trong
một thời gian hạn định. Trước tình hình dịch bệnh COVID-19 diễn biến hết sức phức tạp, xác
định trách nhiệm tham gia bảo vệ sức khỏe cộng đồng nên nhà máy đã nâng cao năng lực sản
xuất bằng cách tiến hành cải tiến kỹ thuật đồng thời kết hợp tăng ca để quyết tâm rút ngắn thời
gian hoàn thành kế hoạch. Chính vì vậy, trên thực tế mỗi ngày nhà máy đã sản xuất tăng thêm 3
máy nên hoàn thành sớm trước 6 ngày so với kế hoạch được giao. Hỏi theo kế hoạch thì mỗi ngày
nhà máy phải sản xuất bao nhiêu chiếc máy thở. Bài 3: (2,0 điểm)
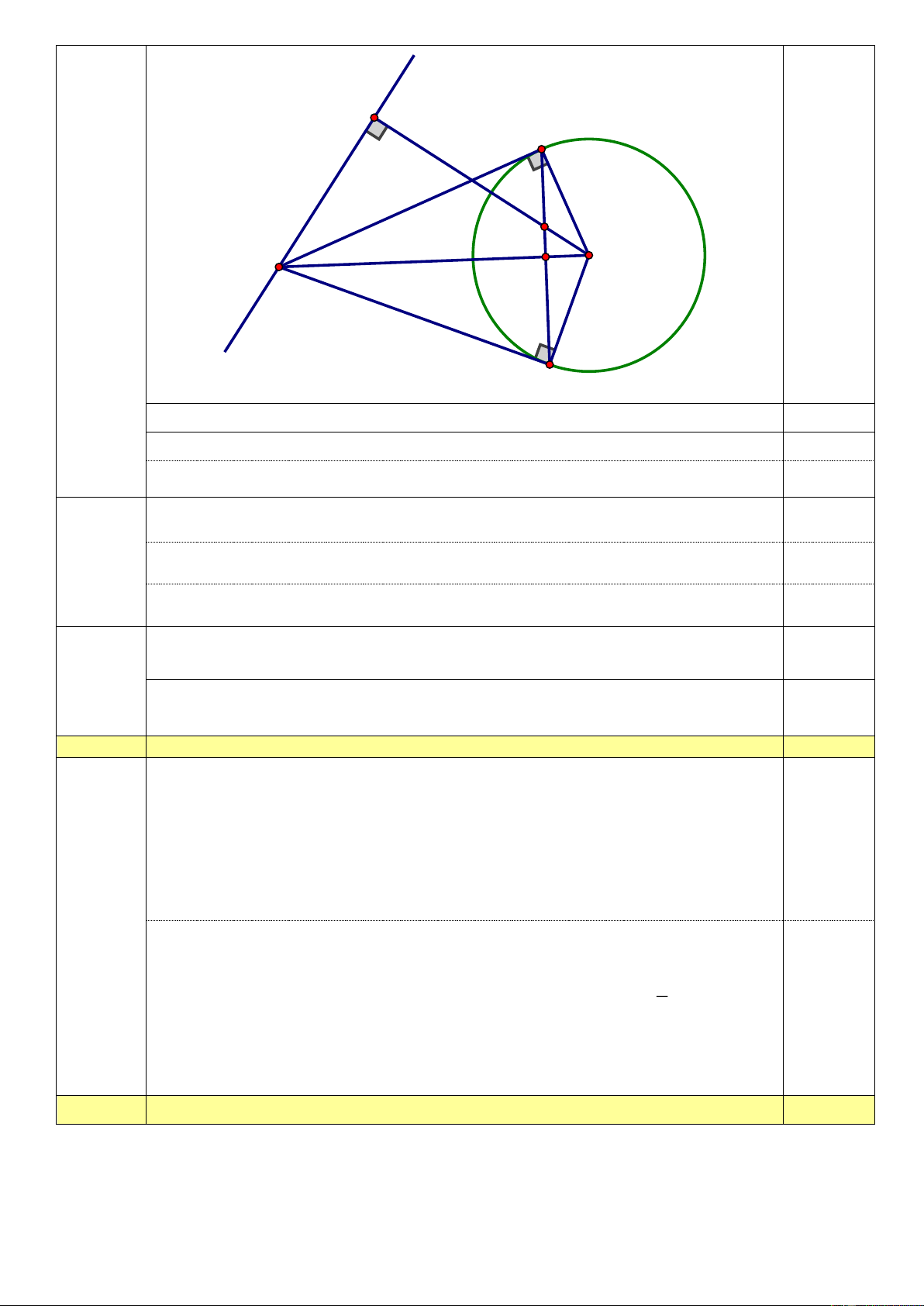
Cho đường tròn tâm O, đường kính AB. Trên (O) lấy C không trùng với A, B sao cho CA
> CB. Các tiếp tuyến của đường tròn tại A, tại C cắt nhau tại D. Kẻ CH vuông góc với AB , DO cắt AC tại E.
1/ Chứng minh rằng : Tứ giác OECH nội tiếp.
2/ CD cắt AB tại F. Chứng minh rằng: o 2BCF CFB 90 .
3/ BD cắt CH ở M. Chứng minh rằng: ME song song AB.
…………………………Hết…………………………… Trang 7 ĐÁP ÁN
I-TRẮC NGHIỆM (6,0 điểm) Đúng mỗi câu ghi 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B B C B C B A D D B A A Câu 13 14 15 16 17 18 19 20 21 22 23 24 Đáp án C B C C A D B C C A B A
II-TỰ LUẬN (4,0 điểm): Bài Đáp án Thang (điểm) điểm Bài 1
1/ Giải hệ phương trình x y 6 { (1,0 đ) 2x y 3 x y 6 y 3 { { 3x 9 x 0,25 đ 3
Vậy hệ phương trình có nghiệm duy nhất là ( x = 3 ; y = 3 ) 0,25 đ
2/ Không giải phương trình, hãy tính tổng và tích hai nghiệm của
phương trình sau: x2 – 7x + 12 = 0.
Ta có: 1 0 0,25 đ
Suy ra phương trình có hai nghiệm phân biệt x ; x 1 2 x x 7 0,25 đ
Theo hệ thức Viet ta có: 1 2 { x x 12 . 1 2 Bài 2
Gọi x (chiếc) là số máy thở nhà máy sản xuất trong mỗi ngày theo kế
(1,0 đ) hoạch. Điều kiện * x . 0,25 đ
Vậy số chiếc máy thở nhà máy sản xuất trong mỗi ngày trên thực tế là: x+3 ( chiếc) 360
Theo kế hoạch, thời gian nhà máy sản xuất là: (ngày) x 360
Thực tế, thời gian nhà máy sản xuất là: x (ngày) 3 360 360
Theo bài ra, ta có phương trình: 6 x x 3 0,25 đ 2
x 3x 180 0
Giải phương trình ta được x 12 (TMĐK) và x 15 (KTMĐK) 0,25 đ 1 2
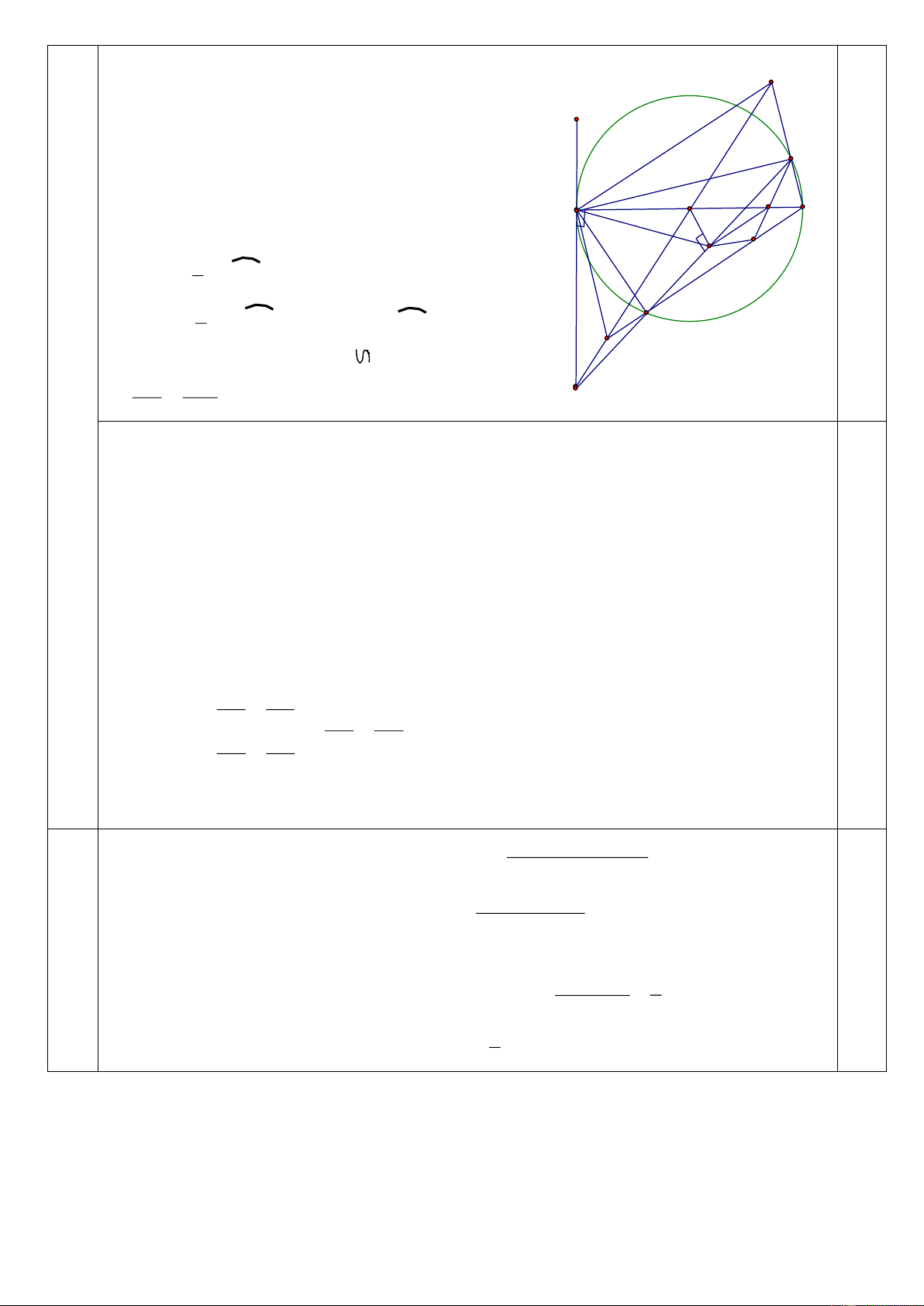
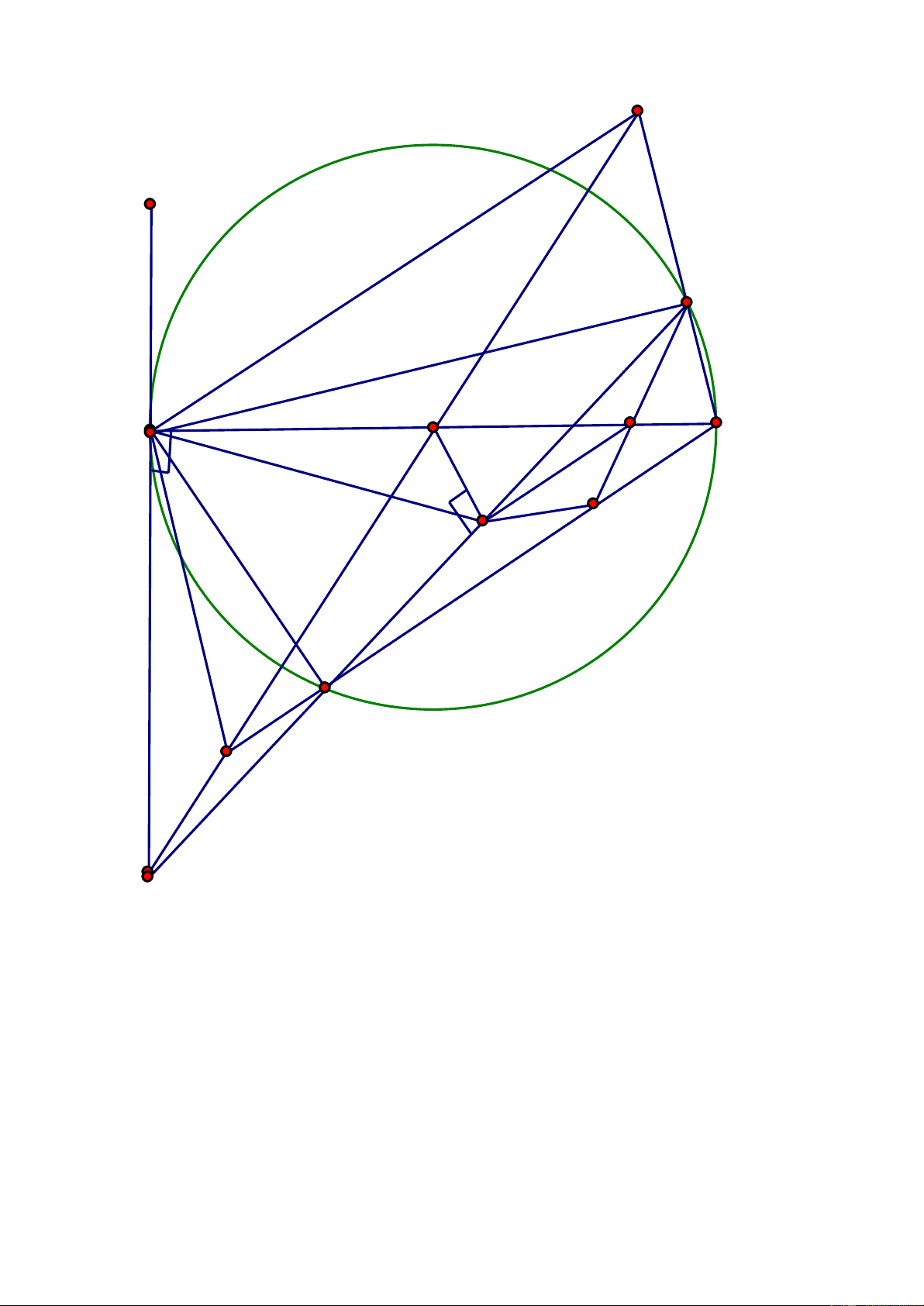
Vậy theo kế hoạch, mỗi ngày nhà máy sản xuất 12 chiếc máy thở. 0,25 đ Trang 8 Bài 3 K (2,0 đ) 1 D 1 C 2 E M 1 A H O B F
Hình vẽ đúng đến câu a 0,25 đ
1/ Chứng minh rằng : Tứ giác OECH nội tiếp.
Chứng minh được: OD là đường trung trực của đoạn AC Suy ra: AC DO tại E 0,25 đ 0 CEO 90 Mà: 0
CHO 90 (vì CH AB) 0,25 đ 0
CEO +CHO 180 0,25 đ
Suy ra: Tứ giác OECH nội tiếp
2/ CD cắt AB tại F. Chứng minh rằng : o 2BCF CFB 90 . 1 Ta có: BCF
sđ BC ( tính chất góc tạo bỡi tia tiếp tuyến và dây cung). 2
2BCF sđ BC 0,25 đ 1 1 Và: CFB
sđ AC sđ BC (tính chất góc có đỉnh bên ngoài đường 2 2 tròn). 1 1
2BCF +CFB = sđ BC +
sđ AC sđ BC 2 2 0,25 đ 1 1 1
sđ AC sđ BC sđ AB = 900 2 2 2
3/ BD cắt CH ở M. Chứng minh rằng: ME song song AB.
Gọi K là giao điểm của AD và BC.
Ta có: OA=OB (bán kính); OD BK (cùng vuông góc với AC) 0,25 đ Suy ra: AD = DK (1) Mà: CH
AK (cùng vuông góc với AB) MH MC BM ( ) (2) AD DK BD 0,25 đ
Từ (1) và (2) ta có: MH = MC
Ta cũng có: EA = EC (vì OD là đường trung trực của đoạn AC) ME AB. Trang 9 ĐỀ 3
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
I/ PHẦN TRẮC NGHIỆM:(2,0 điểm) Khoanh tròn vào chữ cái đầu câu mà em chọn
Câu 1: Cho hàm số y = 4x2. Điểm nào sau đây thuộc đồ thị hàm số A. (4; 32) B. (– 2; 16) C. (–2; – 16) D. Hai câu A, C đúng
Câu 2. Cho đều ABC nội tiếp đường tròn tâm O. Tiếp tuyến Ax (A là tiếp điểm; cung ABC là
cung chứa góc CAx) số đo góc ngoài CAx là: :
A. góc CAx = 300 B. góc CAx = 600
C. góc CAx = 900 D. góc CAx = 1200
Câu 3. Đồ thị hàm số nào đi qua gốc tọa độ O(0;0) A. y = 2x – 1 B. y = 2x C. y = 2x2
D. hai câu A, B đều đúng.
Câu 4: Góc có đỉnh nằm trong đường tròn thì bằng A.
Tổng số đo hai cung bị chắn.
C. Hiệu số đo hai cung bị chắn. B.
Nửa tổng số đo hai cung bị chắn.
D. Nửa hiệu số đo hai cung bị chắn.
Câu 5: Điểm A(–4; 4) thuộc đố thị hàm số y = ax2. Vậy a bằng 1 1 A. a = B. a = – C. a = 4 D. a = – 4 4 4
Câu 6. ABC nội tiếp đường tròn đường kính AB thì A. góc A = 900 B. góc C = 900 C. góc B = 900 D. ba câu A, B, C sai
Câu 7: Trong các hàm số sau, hàm số nào đồng biến khi x < 0?
A. y = -2x B. y = -x + 10
C. y = ( 3 - 2)x2 D . y = 3 x2
Câu 8: Tứ giác ABCD nội tiếp đường tròn có góc A = 400 ; góc B = 600 Khi đó góc C – góc D bằng A. 300 B . 200 C . 1200 D . 1400
II/ Phần tự luận: (8,0điểm)
Câu 1 (1đ) Giải hệ phương trình
3x 2y 2 a.
Bằng phương pháp cộng đại số: 2x y 3
; b. Bằng phương pháp thế:
x y 6
2x y 1 1
Câu 2 (1,5đ). a, Vẽ đồ thị hàm số 2 y x (P) 2
b, Tìm giá trị của m sao cho điểm C(-2; m) thuộc đồ thị (P)
c, Tìm tọa độ giao điểm của đường thẳng y = x - 0,5 và parabol (P)
Câu 3 (1,5 đ) Hai công nhân cùng làm một công việc thì 6 ngày xong. Nhưng nếu người thứ 4
nhất làm 4 ngày rồi nghỉ, người thứ hai làm tiếp 6 ngày thì mới hoàn thành được công việc. 5
Hỏi nếu làm một mình mỗi người làm xong công việc đó trong bao lâu?
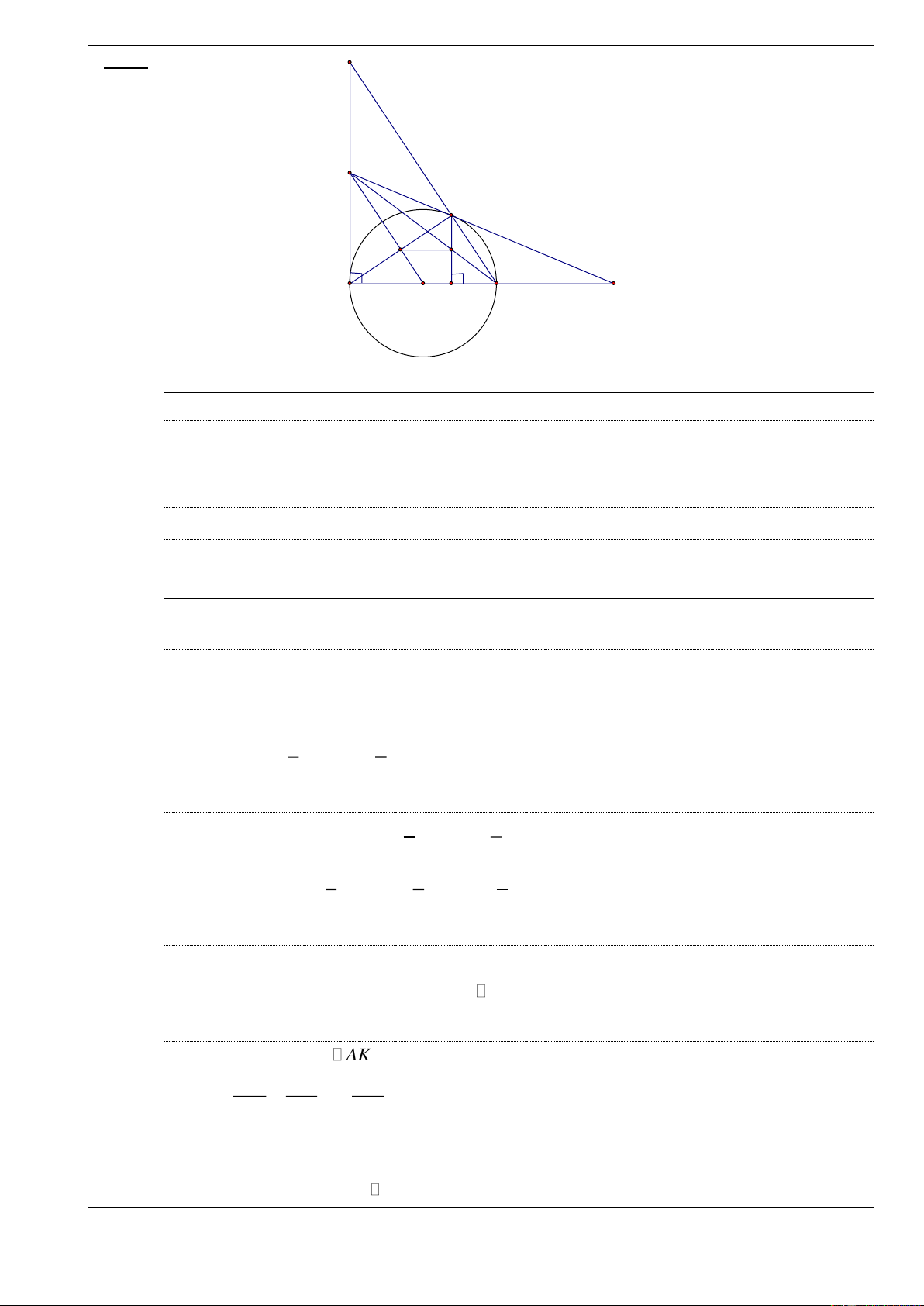
Câu 4. (3,5 đ). Cho đường tròn tâm O, đường kính BC, Lấy điểm A trên cung BC sao cho AB <
AC . Trên OC lấy điểm D, từ D kẻ đường thẳng vuông góc với BC cắt AC tại E .
a) Chứng minh : góc BAC = 900 và tứ giác ABDE nội tiếp?
b) Đường cao AH của tam giác ABC cắt đường tròn tại F. Chứng minh HF.DC = HC.ED?
c) Chứng minh BC là tia phân giác của góc ABF? 2
xy 4 8 y
Câu 5. (0,5đ) Giải hệ phương trình: 2
xy 2 x Đáp án: Câu
Nội dung – Đáp án Điểm
TRẮC NGHIỆM (mỗi câu 0,25 đ)
1-B ; 2-D ; 3-B ; 4-B ; 5-A ; 6-B; 7-C; 8-B 2,0 Trang 10
TỰ LUẬN (8 điểm) Câu 1 3𝑥 = 9 0,25
a) 2x y 3 {
x y 6 𝑥 − 𝑦 = 6 0,25 𝑥 = 3 {𝑦 = −3
Vậy phương trình đã cho có nghiệm duy nhất là (x;y) = (3; -3)
3x 2y 2 3𝑥 − 2(2𝑥 − 1) = 2 b) { 0,25 2x y 1 𝑦 = 2𝑥 − 1 𝑥 = 0 { 0,25 𝑦 = −1
Vậy phương trình đã cho có nghiệm duy nhất là (x;y) = (0; -1)
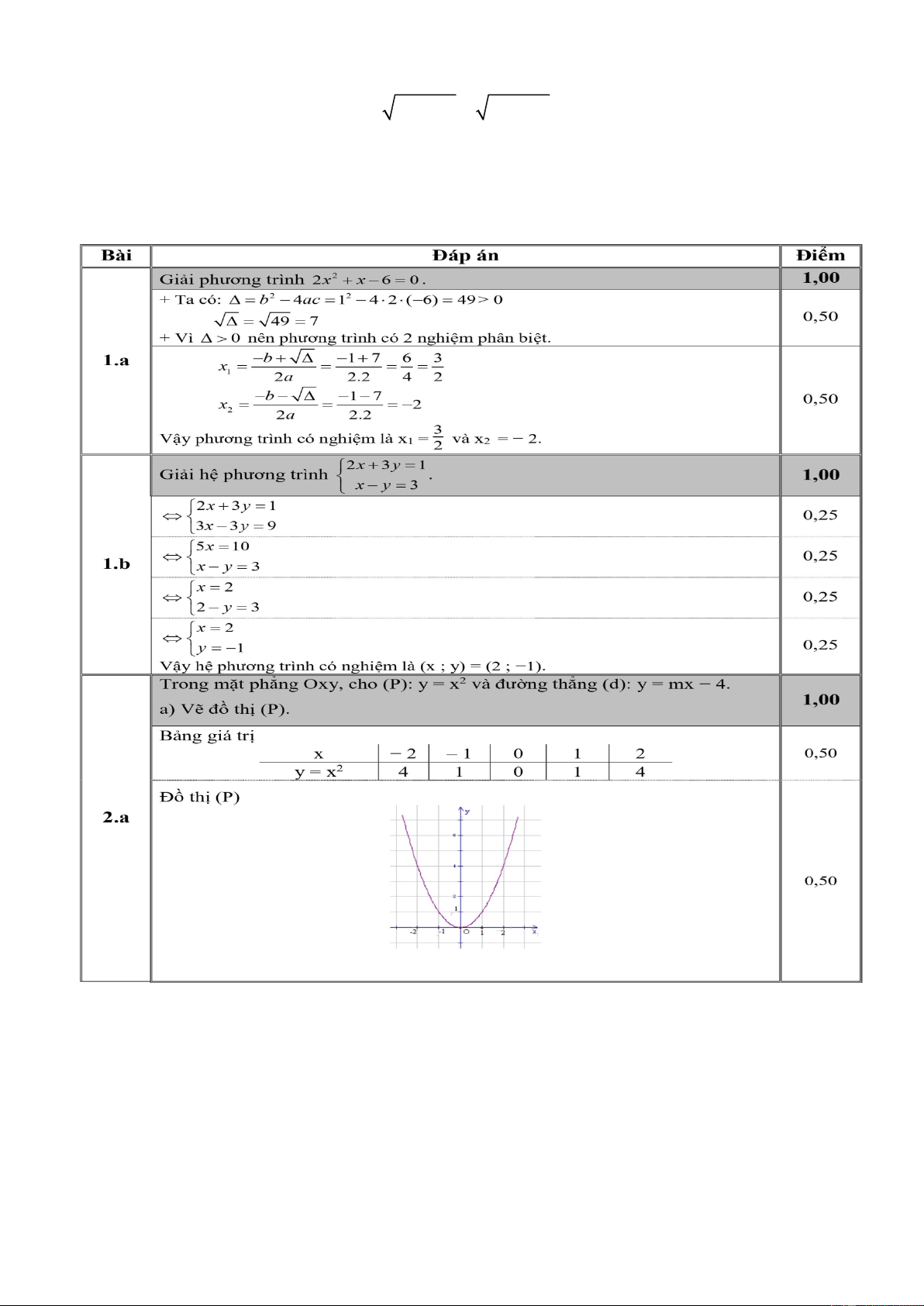
Câu 2 a)Lập bảng các giá trị -4 -2 2 4 1 2 0,25 y = x 8 2 0 2 8 2 10 y y 8 0,25 6 4 2 x x O -10 -5 -4 4 -2 2 5 10 -2 1 -4 Đồ thị hàm số y = 2
x là đường parabol có đỉnh là gốc toạ độ O, nhận trục 2
tung làm trục đối xứng, nằm phía trên trục hoành vì a >0 -6 1
b) Vì C (-2 ; m) thuộc parabol (p) nên ta có m = ( 2 2) m = 2 0, 5 2
Vậy với m = 2 thì điểm C ( -2; 2) thuộc parabol (p)
c, Hoành độ giao điểm của parabol (p) và đường thẳng y = x - 0,5 là nghiệm 0,25 1 của phương trình: 2 x = x - 0,5 2 2 x = 2x - 1 2 x - 2x + 1 = 0 2 (x 1) = 0 x - 1 = 0 x = 1 0,25 Trang 11
Thay x = 1 vào y = x - 0,5 ta được y = 0,5
Vậy tọa độ giao điểm là ( 1 ; 0,5) Câu 3
Gọi thời gian hai công nhân làm xong công việc nếu làm một 0,25
mình lần lượt là a và b (ngày) (a, b>0)
Nếu làm một mình trong 1 ngày người thứ nhất làm được 1 công 𝑎 việc.
Người thứ hai làm được 1 công việc 𝑏
Hai công nhân cùng làm chung công việc hết 6 ngày xong nên ta có: 0,25 6. 1 1 +6. = 1 (1) 𝑎 𝑏
Người thứ nhất làm 4 ngày rồi nghỉ, người thứ 2 làm tiếp 6 ngày thì hoàn thành được
4545 công việc nên ta có: 0,25 4. 1 1 +6. = 4 (2) 𝑎 𝑏 5
Từ (1) và (2) ta có hệ phương trình: 1 1 6. + 6. = 1 { 𝑎 𝑏 1 1 4 0,25 4. + 6. = 𝑎 𝑏 5 1 1 = 0,25 𝑎 = 10 {𝑎 10 { 1 1 (thỏa mãn điều kiện) = 𝑏 = 15 𝑏 15
Vậy nếu làm 1 mình thì người thứ nhất hoàn thành công việc 0,25
trong 10 ngày, người thứ hai hoàn thành công việc trong 15 ngày. Câu 4 Vẽ hình đúng 0,5
a) Chỉ ra được góc BAC nội tiếp chắn nửa đường tròn. 0,5 Suy ra : góc BAC=900 0,5
Xét tứ giác ABDE có 𝐵𝐴𝐶 ̂ + 𝐵𝐷𝐸 ̂ = 1800
Suy ra tứ giác ABDE nội tiếp 0,75
b) – chứng minh được ∆𝐴𝐻𝐶 đồ𝑛𝑔 𝑑ạ𝑛𝑔 ∆𝐷𝐸𝐶 (𝑔. 𝑔) 0,5 0,5
- Chứng minh được AH=HF .suy ra được HF.DC = HC.ED 0,25
c) Chứng minh được góc ABC= góc FBC.
Suy ra BC là tia phân giác của góc ABF. Câu 5 2 2 x
Ta có: xy = 2 + x2 2 nên xy 0 và y
Thay giá trị này vào pt thứ x 0,25 2 2 2 2 nhất ta có: 2 x 2 x 2 x 2 8 . Do 2
x 2 0 nên 8 - 0 x x
( 2 + x2)2 8x2 x4 - 4x2 + 4 0 ( x2 - 2)2 0
( x2 - 2)2 = 0 ( vì ( x2 - 2)2 ) 0
x2 = 2 x 2; x 2
Nếu x 2 thì y 2 2 , Nếu x 2 thì y 2 2 , 0,25 1 1 2 2 Trang 12
Vậy hệ có hai nghiệm (x ; y) là ( 2 ; 2 2 ), ( 2 ; 2 2 )
Lưu ý: học sinh làm đúng cách khác vẫn được điểm tối đa. ĐỀ 4
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3 điểm) x + y = 5
Câu 1. Giải hệ phương trình được nghiệm là : 2x - y = 4 x = -3 x = 3 x = 3 x = -3 A. ; B. ; C. ; D. . y = 2 y = 2 y = -2 y = -2 1
Câu 2. Cho hàm số y = - 2
x . Kết luận nào sau đây là đúng ? 2
A. Hàm số luôn nghịch biến ;
B. Hàm số luôn đồng biến ;
C. Giá trị của hàm số luôn âm ;
D. Hàm số nghịch biến khi x> 0 và đồng biến khi x< 0.
Câu 3. Đồ thị hàm số y = ax2 đi qua điểm A(5; 2). Khi đó a bằng 25 A. B. 1 C. 25 D. 2 2 25 25
Câu 4. Phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì c c A. x1 = 1 , x2 = ; B. x1 = -1 , x2 = - ; a a c c C. x1 = 1 , x2 = - ; D. x1 = -1 , x2 = . a a
Câu 5. Phương trình bậc hai 2x2 –3x + 1 = 0 có các nghiệm là : 1 1 A. x1 = 1, x2 = ; B. x1 = -1, x2 = - ; 2 2 C. x1 = 2, x2 = -3; D. Vô nghiệm.
Câu 6. Gọi x1, x2 là 2 nghiệm của phương trình: 2x2 – 3x – 5 = 0 ta có : 3 5 3 5 A. x1 + x2 = - , x1x2 = - ; B. x1 + x2 = , x1x2 = - ; 2 2 2 2 3 5 2 5 C. x1 + x2 = , x1x2 = ; D. x1 + x2 = , x1x2 = . 2 2 3 2
Câu 7. Hai số u và v có tổng là 10 và tích là 21 thì hai số đó là nghiệm của phương trình : A. x2 + 10x + 21 = 0 ; B. x2 - 21x + 10 = 0 ; C. x2 - 10x - 21 = 0 ; D. x2 - 10x + 21 = 0.
Câu 8. Trên hình 1, hãy chọn đáp án đúng : A A. 1 BAC sđ BnC; B. 1 BAC AC ; 2 2 O C C. 1 BAC
AB ; D. Tất cả các ý trên. 2 B n Hình 1 Trang 13
Câu 9. Trên hình 1, hãy chọn đáp án đúng : x A n A. 1 BAx sđ AmB; B. 1 BAx AnB ; 2 2 B O C. 1 BAx
(sđ AmB - sđ AnB); D. Tất cả đề sai. 2 m Hình 2
Câu 10. Đường tròn bán kính 4cm thì diện tích của nó là : A. 4π (cm2) ; B. 8π (cm2); C. 12π (cm2); D. 16π (cm2).
Câu 11: Số đo góc tạo bởi tia tiếp tuyến và dây cung bằng: A. Nửa sđ cung bị chắn B. sđ cung bị chắn
C. Nửa sđ góc nội tiếp cùng chắn một cung
D. sđ góc ở tâm cùng chắn một cung
Câu 12: Câu nào sau đây chỉ số đo 4 góc của một tứ giác nội tiếp ? A. 0 0 0 0 60 ;105 ;120 ;85 B. 0 0 0 0 75 ;85 ;105 ;95 C. 0 0 0 0 80 ;90 ;110 ;90 D. 0 0 0 0 68 ;92 ;112 ;98
Câu 13. Cho đường tròn (O) đường kính AB, M là điểm nằm trên đường tròn (M khác A và B). Số đo AMB bằng: A. 900 B. 3600 C. 1800 D. 450
Câu 14. Thể tích của hình trụ bán kính 4cm và chiều cao 5cm là : A. π.42.5 ; B. π.4.5 ; C. 2π.4.5 ; D. π.4.52.
Câu 15. Diện tích xung quanh của hình trụ bán kính r và chiều cao h là : A. Sxp = πr2h ; B. Sxp = πrh ; C. Sxp = 2πrh ; D. Sxp = πrh2.
II. PHẦN TỰ LUẬN (7 điểm)
Bài 1 (1,0 điểm): (Không dùng máy tính cầm tay) a) Giải phương trình 2
2x x 6 0 .
2x 3y 1
b) Giải hệ phương trình x y 3
Bài 2 (1,0 điểm): Trong mặt phẳng Oxy, cho parabol (P): y = x2 và đường thẳng (d): y = mx − 4. a) Vẽ đồ thị (P).
b) Xác định m để (d) tiếp xúc với (P).
Bài 3 (1,5 điểm):
Cho phương trình x2 − (m + 4)x + 3m + 3 = 0 (1) (với m là tham số).
a) Chứng minh phương trình (1) luôn có nghiệm với mọi giá trị của m.
b) Gọi x ; x là hai nghiệm của phương trình (1).Tìm tất cả các giá trị dương của m 1 2 để biểu thức 2 2
x x x x 8 1 1 2 2
Bài 4 (3,00 điểm):
Từ điểm M ở ngoài đường tròn (O), kẻ hai tiếp tuyến MA và MB với đường tròn (O) , A và
B là các tiếp điểm. Gọi E là trung điểm của đoạn thẳng MB; C là giao điểm của AE và (O)
(điểm C khác điểm A), H là giao điểm của AB và MO.
a) Chứng minh 4 điểm M, A, O, B cùng thuộc một đường tròn. b) Chứng minh EB2 = EC.EA.
c) Chứng minh HCEB là một tứ giác nội tiếp.
d) Gọi D là giao điểm của MC và (O) (điểm D khác điểm C). Chứng minh ABD là tam giác cân.
Bài 5 (0,50 điểm): Cho a, b > 0 thỏa mãn a + b ≤ 2. Tìm giá trị lớn nhất của biểu Trang 14 thức P
a(b 1) b(a 1) ---HẾT---
(Đề có 01 trang. Giáo viên coi kiểm tra không giải thích gì thêm) ĐÁP ÁN Trang 15 Trang 16 Trang 17 ĐỀ 5
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 Thuvienhoclieu.com MÔN TOÁN 9
Câu 1 (3,0 điểm).
Nêu tính chất của hàm số y = ax2 (a ≠ 0)
Cho phương trình: ax2 + bx + c = 0 ( a ≠ 0) có 2 nghiệm x1 và x2.
Viết công thức tính : Tổng x1 + x2 và tích x1. x2 theo a, b, c Trang 18
Cho phương trình x2 + 7x - 4 = 0
Không giải phương trình hãy tính x1 + x2 và x1.x2.
Câu 2: (1,0 điểm). Vẽ đồ thị hàm số (P)
Câu 3 (2,0 điểm). Giải phương trình, hệ phương trình sau a) b)
Câu 4 (3,0 điểm).
Cho ABC có ba góc nhọn nội tiếp đường tròn tâm O bán kính R.. Các phân giác của các góc
ABC , ACB lần lượt cắt đường tròn tại E, F.
1. CMR: OF AB và OE AC.
2. Gọi M là giao điểm của của OF và AB; N là giao điểm của OE và AC. CMR: Tứ
giác AMON nội tiếp và tính diện tích hình tròn ngoại tiếp tứ giác này.
3. Gọi I là giao điểm của BE và CF; D là điểm đối xứng của I qua BC. CMR: ID MN.
Câu 5 (1,0 điểm).Một hình trụ có bán kính đáy là 7 cm, chiều cao của hình trụ là10cm .
Tính diện tích xung quanh của hình trụ đó. ĐÁP ÁN Câu Đáp án Điểm Câu 1 Cho hàm số (3 điểm)
-Nếu a > 0 thì hàm số nghịch biến khi x < 0 thì hàm số đồng 1đ biến khi x > 0
-Nếu a < 0 thì hàm số đồng biến khi x < 0 thì hàm số nghịch biến khi x > 0
Viết đúng ct tổng và tích 2 nghiệm 1đ
c. Phương trình có a.c = 1.(-4) = -4 < 0
=> Phương trình có hai nghiệm phân biệt x1, x2 1đ +Theo viet: x1 + x2 = = -7 x1.x2 = = -4 Câu 2 0.5đ
(1 điểm) Lập bảng giá trị đúng x - 2 - 1 0 1 2 y = x2 4 1 0 1 4 Vẽ đúng (P) (P) : 0.5đ Câu 3 (2 điểm) 1
= (-5)2 – 4.3 = 25 – 12 = 13 > 0 Trang 19
Vì > 0 nên phương trình có 2 nghiệm phân biệt Ta có: 1
Vậy hệ phương trình đã cho có nghiệm duy nhất . o.5đ
vẽ hình, ghi GT KL A 1,0đ F M N E 1) Chứng minh: O I + (O,R) có: B C ACF . n tiep chăn AF D BCF . n tiep chăn BF
AF BF OF AB
ACF BCF (CF laphân giac) Câu 4 + (O,R) có: ABE . n tiep chăn AE CAE . n tiep chăn CE
AE CE OE AC 0,5đ
ABE CAE (BE la phân giac)
2. CMR: Tứ giác AMON nội tiếp: 0
OF AB tai M OMA 90 0
OMA ONA 180 Tứ 0.5đ 0
OE AC tai N ONA 90 AMON nội tiếp.
* Tính diện tích hình tròn ngoại tiếp tứ giác AMON:
Tứ giác AMON nội tiếp đường tròn đường kính OA OA2 2 OA 2 R 0,5đ S . . . 2 4 4
3. CMR: ID MN:
+ I và D đối xứng nhau qua BC ID BC (1) + (O,R) có: Trang 20 1
OF AB taïi M MA MB AB 2
MN là đường trung bình 1
OE AC taïi N NA NC AC 2
của ABC MN // BC (2).
Từ (1) và (2) ID MN . 0,5 Câu 5 (1điểm) 0,5 ĐỀ 6
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 Thuvienhoclieu.com MÔN TOÁN 9
I. PHẦN TRẮC NGHIỆM: (3,0 điểm - thời gian làm bài 25 phút)
(Chọn câu trả lời đúng nhất rồi ghi vào giấy làm bài)
Câu 1. Hệ phương trình nào sau đây vô nghiệm: x y 0 x y 4
4x 4y 4 x y 4 A.
x y B. 0
x y C. 0 x y D. 0
x y 0
Câu 2. Cho hàm số y = 2x2, khi đó:
A. Hàm số luôn đồng biến
B. Hàm số đồng biến khi x > 0
C. Hàm số luôn nghịch biến
D. Hàm số đồng biến khi x < 0
Câu 3. Phương trình x2 - 7x - 8 = 0 có tổng hai nghiệm là: 7 A. 8 B. 7 C. –7 D. 2
Câu 4. Cho đường tròn có bán kính 6 cm. Chiều dài cung tròn có số đo 600 là: A. 4π (cm) B. 3π (cm) C. 2π (cm) D. π (cm)
Câu 5. Cho đường tròn (O; R) có hai bán kính OA, OB vuông góc nhau. Diện tích hình quạt OAB là: 2 R 2 R 2 R A. B. C. D. 2 R 2 3 4
Câu 6. Tam giác ABC cân tại A, có 0
BAC 30 nội tiếp đường tròn (O). Số đo cung AB là: A. 600 B. 750 C. 12000 D. 1500
Câu 7. Trong hình vẽ, biết AB là đường kính của đường tròn tâm O. C 0
ACD 50 số đo góc x bằng: 0 50 B A. 300 B. 400 C. 500 D. 450 O x A D
Câu 8. Cho tam giác ABC vuông tại A. Tâm của đường tròn ngoại tiếp tam giác ABC là:
A. trung điểm AB
B. trọng tâm tam giác ABC
C. trung điểm BC D. trung điểm AC Trang 21
Câu 9. Cặp số (1; – 2) là nghiệm của phương trình: A. 3x + 0y = 3
B. x – 2y = –7 C. 0x + 2y = 4 D. x – y = 0
x 2y 3
Câu 10. Cặp số nào sau đây là nghiệm của hệ phương trình y 1 A. (2 ; 1) B. (2 ; – 1) C. (1 ; – 1) D. (1 ; 1)
Câu 11. Phương trình x2 – 2x + m = 0 có nghiệm kép khi: A. m = 1. B. m = - 1.
C. m 1 D. m 1
Câu 12. Phương trình ax2 + bx + c = 0 a 0có nghiệm x =1 khi:
A. a + b + c = 0.
B. a - b + c = 0.
C. a - b - c = 0. D. a + b - c = 0.
B. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm) x y
a) Không dùng máy tính cầm tay, giải hệ phương trình 2 3 .
x 3y 2
b) Cho phương trình: x2 - x + m = 0 (m là tham số ).
i) Giải phương trình trên khi m = 6.
ii) Tìm giá trị của tham số m để phương trình có hai nghiệm phân biệt x , x thỏa 1 2
x x x x 5 1 2 1 2
Bài 2. (2,0 điểm) Cho parabol (P): y = x2 và đường thẳng (d): y = -2x + 3.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (d) và (P) bằng phép tính.
Bài 3. (2,5 điểm) Cho đường tròn tâm O. Lấy điểm A ở ngoài đường tròn (O), đường thẳng AO
cắt đường tròn (O) tại hai điểm B và C (B nằm giữa A và C). Qua A vẽ đường thẳng không đi qua
O cắt đường tròn (O) tại hai điểm phân biệt D và E (D nằm giữa A và E). Đường thẳng vuông
góc với AB tại A cắt đường thẳng CE tại F.
a) Chứng minh tứ giác ABEF nội tiếp.
b) Gọi M là giao điểm thứ hai của đường thẳng FB với đường tròn (O). Chứng minh rằng AF // DM. c) Chứng minh CE.CF = CB.CA
d) Chứng minh rằng CE.CF + AD.AE = AC 2 .
Bài 4. ( 0,5 điểm ) Để tiết kiệm nguyên liệu dùng làm vỏ lon (hình trụ) để
đựng sữa, nhà sản xuất phải thiết kế hộp sữa sao cho diện tích toàn phần
của hình trụ không đổi nhưng bên trong phải chứa đựng được thể tích sữa
nhiều nhất. Theo em nhà sản xuất phải thiết kế lon sữa có mối quan hệ
giữa bán kính đáy R và chiều cao h như thế nào để đạt yêu cầu nói trên? - HẾT – ĐỀ 7
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9 Trang 22
Câu 1. (2 điểm) Giải phương trình và hệ phương trình 5𝑥 − 3𝑦 = 1 1/ 6x2 – 13x – 5 = 0 2/ { 4𝑥 + 5𝑦 = 23
Câu 2. (1,5 điểm) Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x2
1/ Vẽ (P) trên hệ trục tọa độ và tìm các điểm A trên (P) có tung độ bằng 3 lần hoành độ
2/ Tìm m để đường thẳng (d): y = 4x + m – 3 tiếp xúc với (P)
Câu 3. (1,5 điểm) Cho phương trình x2 + 2x + m – 1 = 0
1/ Tìm m để phương trình có 2 nghiệm phân biệt x1 và x2 2/ Tìm m để: 𝑥2 2
1 . (𝑥1 + 1) + 𝑥2 . (𝑥2 + 1) = –20
Câu 4. (1,5 điểm) Bác Hai sở hữu 1 mảnh đất hình chữ nhật. Nếu tăng chiều rộng thêm 3m
và tăng chiều dài thêm 2m thì diện tích mảnh đất tăng 96m2 so với ban đầu. Nếu tăng chiều rộng
thêm 4m và giảm chiều dài đi 5m thì diện tích mảnh đất giảm 15m2 so với ban đầu. Bác dành ra
35% mảnh đất để trồng đậu, 45% mảnh đất để trồng cà rốt và phần đất còn lại thì cho thuê. Tìm
diện tích mảnh đất bác cho thuê.
Câu 5. (0,5 điểm) Một hồ nước hình tròn tâm là O có 1 cây cầu AB bắc ngang (A, B ở vị trí bờ hồ sao cho 𝐴𝑂𝐵
̂ = 1200. Hỏi 1 người đi từ A đến B bằng cách đi qua cầu với vận tốc là v
hoặc đi theo vòng quanh bờ hồ với vận tốc là 1,5v (cung tròn gần AB hơn) thì đi cách nào sẽ nhanh hơn ? Tại sao.
Câu 6. (3 điểm) Cho tam giác ABC có 3 góc nhọn (AB < AC và AB < BC) nội tiếp đường
tròn (O;R) có 2 đường cao AD và BE cắt nhau tại H, CH cắt AB tại F.
1/ Chứng minh: tứ giác BFEC nội tiếp trong 1 đường tròn, xác định tâm I đường tròn này
2/ Chứng minh: FC là tia phân giác 𝐸𝐹𝐷 ̂ và AF.AB = AE.AC
3/ EF cắt BC tại S. Tiếp tuyến tại B của đường tròn (I) cắt FC và AS lần lượt tại P và M.
Chứng minh: ME là tiếp tuyến của (I)
4/. Đường thẳng qua D song song với BE cắt BM tại N. Đường tròn ngoại tiếp tam giác
tam giác MNE cắt BE tại điểm thứ hai là K. Đường thẳng qua B song song với AC cắt
DF tại Q. Chứng minh: OK _|_ PQ
&&&-------------------HẾT-------------------&&&
Đáp án đề thi tham khảo Câu 1 1/ 6x2 – 13x – 5 = 0
∆ = (–13)2 – 4.6. –5 = 289 > 0, √∆= √289 = 17 13+17 5 13−17 −1
=> Phương trình có 2 nghiệm phân biệt: x = = 1 = ; x 6.2 2 2 = 6.2 3 Trang 23 5𝑥 − 3𝑦 = 1 20𝑥 − 12𝑦 = 4 −37𝑦 = −111 2/ { { { 4𝑥 + 5𝑦 = 23 −20𝑥 − 25𝑦 = −115 5𝑥 − 3𝑦 = 1 𝑦 = 3 𝑦 = 3 𝑦 = 3 { { { 5𝑥 − 3.3 = 1 5𝑥 = 10 𝑥 = 2 Câu 2
1/ Bảng giá trị của (P): y = x2 x – – 0 1 2 2 1 y 4 1 0 1 4
Theo đề bài ta có: yA = 3xA => x 2 A = 3xA xA.(xA – 3) = 0 xA = 0 hoặc xA = 3 Với xA = 0 => yA = 0
Với xA = 3 => yA = 32 = 9
Vậy tọa độ điểm A cần tìm là: (0; 0) và (3 ; 9)
2/ Phương trình hoành độ của (P) và (d): y = 4x + m – 3 là:
x2 = 4x + m – 3 x2 – 4x – m + 3 = 0 (*)
∆ = (–4)2 – 4.1.( –m + 3) = 16 + 4m – 12 = 4 + 4m
Để (P) tiếp xúc với (d) phương trình (*) có nghiệm kép
∆ = 0 4 + 4m = 0 4m = –4 m = –1 Câu 3. x2 + 2x + m – 1 = 0 (*)
1/ ∆ = 22 –4.1.(m – 1) = 4 – 4m + 4 = 8 – 4m
Để (*) có 2 nghiệm phân biệt ∆ > 0 8 – 4m > 0 4m < 8 m < 2
2/ Theo định lí viet ta có: x1 + x2 = –2 ; x1.x2 = m – 1 𝑥2 2
1 + 𝑥2 = (𝑥1 + 𝑥2)2 − 2𝑥1. 𝑥2 = (–2)2 – 2.(m – 1) = 4 – 2m + 2 = 6 – 2m 𝑥3 3 2 2
1 + 𝑥2 = (𝑥1 + 𝑥2). (𝑥1 + 𝑥2 − 𝑥1. 𝑥2) = –2.(6 – 2m – m + 1)
= –2.(7 – 3m) = –14 + 6m. Theo đề bài: 𝑥2 2 3 3 2 2
1 . (𝑥1 + 1) + 𝑥2 . (𝑥2 + 1) = –20 𝑥1 + 𝑥2 + 𝑥1 + 𝑥2 = –20
–14 + 6m + 6 – 2m = –20 4m = –12 m = –3 < 2 (nhận) Câu 4.
Gọi x (m) và y (m) lần lượt là chiều rộng và chiều dài mảnh đất ban đầu (y > x > 0)
Diện tích mảnh đất ban đầu là: xy (m2)
Diện tích mảnh đất theo giả định thứ nhất là: (x + 3)(y + 2) (m2)
Diện tích mảnh đất theo giả định thứ hai là: (x + 4)(y – 5 ) (m2) Trang 24
(𝑥 + 3)(𝑦 + 2) = 𝑥𝑦 + 96
Theo đề bài ta có hệ phương trình: {
(𝑥 + 4)(𝑦 − 5) = 𝑥𝑦 − 15
𝑥𝑦 + 2𝑥 + 3𝑦 + 6 = 𝑥𝑦 + 96 2𝑥 + 3𝑦 = 90 10𝑥 + 15𝑦 = 450 { { {
𝑥𝑦 − 5𝑥 + 4𝑦 − 20 = 𝑥𝑦 − 15 −5𝑥 + 4𝑦 = 5 −10𝑥 + 8𝑦 = 10 2𝑥 + 3𝑦 = 90 2𝑥 + 3.20 = 90 2𝑥 = 30 𝑥 = 15 { { 23𝑦 = 460 𝑦 = 20
{ 𝑦 = 20 {𝑦 = 20
(Nhận thỏa điều kiện y > x > 0).
Diện tích mảnh đất ban đầu của bác Hai là: 15.20 = 300m2
Diện tích mảnh đất bác Hai cho thuê là: 300.(1 – 0,35 – 0,45) = 60m2 Câu 5.
Gọi R là bán kính của hồ nước, kẻ OI _|_ AB tại I. Gọi t là thời gian đi từ A qua B
=> IA = IB (quan hệ đường kính và dây cung) => AB = 2IA
Tam giác IAB cân tại I có OI là đường cao => OI là đường phân giác 𝐴𝑂𝐵 ̂ 𝐴𝑂𝐵 ̂ 1200 => 𝐴𝑂𝐼 ̂= = = 600. 2 2
Tam giác AOI vuông tại I => AB = 2AI = 2OA.cosAOI = 2R.cos600 = R√3 120 2𝜋𝑅
Mặt khác độ dài cung nhỏ AB là: l = AB = 2𝜋R. 360 3 𝑅√3 2𝜋𝑅 4𝜋𝑅 t = AB = ; t 𝑣 l(AB) = 3.1,5𝑣 9𝑣 4𝜋𝑅 𝑅√3 So sánh cho: < => t(l 9𝑣 𝑣 AB) < tAB
Kết luận: Đi vòng theo cung tròn của bờ hồ với vận tốc 1,5v nhanh hơn là đi qua cầu với vận tốc v Câu 6 Trang 25
1/ Tứ giác BFEC nội tiếp, xác định tâm I của (BFEC)
Xét tam giác ABC có 2 đường cao AD và BE cắt nhau tại H
=>c H là trực tâm của tam giác ABC => AH _|_ BC
Xét tứ giác BFEC có: 𝐵𝐹𝐶 ̂ = 𝐵𝐸𝐶 ̂ = 900
=> Tứ giác BFEC nội tiếp đường tròn đường kính BC (2 góc bằng nhau cùng nhìn 1 cạnh)
(đpcm) => tâm I của đường tròn ngoại tiếp tứ giác BFEC là trung điểm của cạnh BC (đpcm)
2/ FC là tia phân giác 𝑬𝑭𝑫 ̂ và AF.AB = AE.AC
Xét tứ giác BFHD có: 𝐵𝐹𝐶 ̂ = 𝐴𝐷𝐶
̂ = 900 => Tứ giác BFHD nội tiếp (góc ngoài bằng góc
đối trong) => 𝐷𝐹𝐶 ̂ = 𝐸𝐵𝐶 ̂ Mà 𝐸𝐵𝐶 ̂ = 𝐸𝐹𝐶
̂ (Tứ giác BFEC nội tiếp) => 𝐷𝐹𝐶 ̂ = 𝐸𝐹𝐶
̂ => FC là tia phân giác 𝐸𝐹𝐷 ̂ (đpcm) Xét ∆AEF và ∆ABC: 𝐵𝐴𝐶
̂ là góc chung ; 𝐴𝐸𝐹 ̂ = 𝐴𝐵𝐶
̂ (Tứ giác BFEC nội tiếp) 𝐴𝐸 𝐴𝐹
=> ∆AEF ~ ∆ABC (g – g) => = => AE.AC = AB.AF (đpcm) 𝐴𝐵 𝐴𝐶
3/ ME là tiếp tuyến của (I) Ta có: 𝐵𝐸𝐹 ̂ = 𝐵𝐶𝐹
̂ (Tứ giác BFEC nội tiếp) 𝐵𝐻𝐹 ̂ = 𝐵𝐷𝐹
̂ (Tứ giác BFHD nội tiếp)
IB = IE (I là tâm của (BFEC)) => Tam giác IBE cân tại I => 𝐸𝐵𝐶 ̂ = 𝐵𝐸𝐼 ̂ Trang 26 Mà 𝐵𝐻𝐹 ̂ = 𝐸𝐵𝐶 ̂ + 𝐵𝐶𝐹
̂ (góc ngoài của tam giác BHC)
Từ các chứng minh trên ta có: 𝐵𝐷𝐹 ̂ = 𝐵𝐻𝐹 ̂ = 𝐸𝐵𝐶 ̂ + 𝐵𝐶𝐹 ̂ = 𝐵𝐸𝐼 ̂ + 𝐵𝐸𝐹 ̂ = 𝐼𝐸𝐹 ̂ Xét ∆SDF và ∆SEI: 𝐸𝑆𝐶
̂ là góc chung ; 𝐵𝐷𝐹 ̂ = 𝐼𝐸𝐹 ̂ (cmt) 𝑆𝐷 𝑆𝐸
=> ∆SDF ~ ∆SEI (g – g) => = => SD.SI = SE.SF 𝑆𝐹 𝑆𝐼 Xét ∆SBF và ∆SEC: 𝐸𝑆𝐶
̂ là góc chung ; 𝑆𝐹𝐵 ̂ = 𝐸𝐶𝑆
̂ (Tứ giác BFEC nội tiếp) 𝑆𝐵 𝑆𝐸
=> ∆SBF ~ ∆SEC (g – g) => = => SE.SF = SB.SC 𝑆𝐹 𝑆𝐶 𝑆𝐵 𝑆𝐼
Từ đó suy ra SD.SI = SB.SC => = 𝑆𝐷 𝑆𝐶
Ta có: BM _|_ BC (gt) và AD _|_ BC (gt) => AD // BM 𝑆𝑀 𝑆𝐵 𝑆𝑀 𝑆𝐼 => =
(định lí talet trong tam giác SAD) => = 𝑆𝐴 𝑆𝐷 𝑆𝐴 𝑆𝐶
=> IM // AC (định lí taler đảo trong tam giác SAC). Mà AC _|_ BE (gt) => IM _|_ BE
Tam giác IBE cân tại I có IM là đường cao => IM cũng là đường phân giác của tam giác IBE => 𝐵𝐼𝑀 ̂ = 𝐸𝐼𝑀 ̂ . Xét ∆BIM và ∆EIM: IB = IE(cmt) ; 𝐵𝐼𝑀
̂ = (cmt) ; IM là cạnh chung
=> ∆BIM = ∆EIM (c – g – c ) => 𝐼𝐸𝑀 ̂ = 𝐼𝐵𝑀 ̂ = 900 => EI _|_ EM
Lại có: E thuộc đường tròn (I) => ME là tiếp tuyến của (I) (đpcm) 4/ OK _|_ PQ Xét ∆BDH và ∆BEC: 𝐸𝐵𝐶
̂ là góc chung ; 𝐵𝐷𝐻 ̂ = 𝐵𝐸𝐶 ̂ = 900 𝐵𝐷 𝐵𝐸
=> ∆BDH ~ ∆BEC (g – g) => = => BH.BE = BD.BC 𝐵𝐻 𝐵𝐶
Ta có: BC = 2BI (I là trung điểm của cạnh BC)
IM // AC (cmt) => 𝐵𝐼𝑀 ̂ = 𝐴𝐶𝐵
̂ (2 góc ở vị trí đồng vị) Mà 𝐴𝐶𝐵 ̂ = 𝐵𝐻𝐷
̂ (cùng phụ với 𝐸𝐵𝐶 ̂) => 𝐵𝐼𝑀 ̂ = 𝐵𝐻𝐷 ̂ Xét ∆BIM và ∆DHB: 𝐵𝐼𝑀 ̂ = 𝐵𝐻𝐷 ̂ (cmt) ; 𝐵𝐷𝐻 ̂ = 𝐼𝐵𝑀 ̂ = 900 𝐵𝐼 𝐷𝐻
=> ∆BIM ~ ∆DHB (g – g) => = => BD.BI = BM.HD 𝐵𝑀 𝐵𝐷 Trang 27
Xét tứ giác HBND ta có: ND // BE (gt) và BN // AD (cmt)
=> Tứ giác HBND là hình bình hành => HD = BN Xét ∆MBE và ∆KBN: 𝑀𝐵𝐸 ̂ = 𝐾𝐵𝑁
̂ (2 góc đối đỉnh) ; 𝐸𝑀𝐵 ̂ = 𝐵𝐾𝑁
̂ (2 góc nội tiếp cùng chắn cung EN trong đường tròn EMNK) 𝑀𝐵 𝐵𝐾
=> ∆MBE ~ ∆KBN (g – g) => = => BN.MB = BK.BE 𝐵𝐸 𝐵𝑁
Từ các chứng minh trên ta có:
BH.BE = BD.BC = 2BD.BI = 2BM.HD = 2BM.BN = 2BK.BE => BH = 2BK
Kẻ đường kính BG của (O), HL cắt AC tại G Ta có: 𝐵𝐶𝐺
̂ = 900( góc nội tiếp chắn nửa đường tròn đường kính BG) => BC _|_ CG
Mà AD_|_ BC (gt) => AD // GC. Chứng minh tương tự: AG // FC
Xét tứ giác AHCG có: AD // GC và AG // FC (cmt)
=> Tứ giác AHCG là hình bình hành => LH = LG và LA = LC
Xét tam giác BHG có OB = OG = R và LH = LG (cmt)
=> OL là đường trung bình của tam giác BHG) => BH // OL và BH = 2OL
Mà BH = 2BK (cmt) => OL = BK
Xét tứ giác OLBK có: OL = BK và OL // BH (cmt)
=> Tứ giác OLBK là hình bình hành => OK // BL
Gọi J là trung điểm của cạnh BH, PJ cắt BL và DF lần lượt tại Y và V
J là L lần lượt là trung điểm các cạnh BH và AC nên BH = 2HJ, AC = 2AL. Ta có: 𝐵𝐻𝑃 ̂ = 𝐵𝐴𝐶
̂ (cùng phụ với 𝐵𝐴𝐷 ̂ ) và 𝐴𝑃𝐻 ̂ = 𝐵𝐴𝐶
̂ (cùng phụ với 𝐴𝐵𝑃 ̂) Xét ∆ABC và ∆HPB: 𝐵𝐻𝑃 ̂ = 𝐵𝐴𝐶 ̂ (cmt) ; 𝐴𝑃𝐻 ̂ = 𝐵𝐴𝐶 ̂ (cmt) 𝐴𝐵 𝐻𝑃 𝐴𝐵 𝐻𝑃
=> ∆ABC ~ ∆HPB (g – g) => = => = Do BH = 2HJ và AC = 2AL 𝐴𝐶 𝐻𝐵 𝐴𝐿 𝐻𝐽 Xét ∆ABL và ∆HPJ: 𝐴𝐵 𝐻𝑃 𝐵𝐻𝑃 ̂ = 𝐵𝐴𝐶 ̂ (cmt) ; = (cmt) 𝐴𝐿 𝐻𝐽
=> ∆ABL ~ ∆HPJ (c – g – c) => 𝐴𝐵𝐿 ̂ = 𝐽𝑃𝐻
̂=> Tứ giác FPBY nội tiếp (2 góc bằng nhau
cùng nhìn 1 cạnh) => 𝐵𝑌𝑃 ̂ = 𝐵𝐹𝑃
̂ = 900 => BL _|_ PV tại Y
Tam giác BFH vuông tại F có FJ là đường trung tuyến => JB = JF
Tương tự: JB = JD. Vậy JB = JF = JD.
JB = JF => Tam giác JBF cân tại J => 𝐵𝐹𝐽 ̂ = 𝐴𝐵𝐸 ̂ Trang 28
Tam giác AFC vuông tại F có FL là đường trung tuyến => FL = AL
=> Tam giác AFL cân tại L => 𝐹𝐴𝐶 ̂ = 𝐴𝐹𝐿 ̂ Mà 𝐹𝐴𝐶 ̂ + 𝐴𝐵𝐸
̂ = 900 (Tam giác ABE vuông tại E). Do đó: 𝐽𝐹𝐿 ̂ = 𝐴𝐹𝐵 ̂ − (𝐵𝐹𝐽 ̂ + 𝐴𝐹𝐿 ̂ ) = 1800 − (𝐹𝐴𝐶 ̂ + 𝐴𝐵𝐸 ̂) = 1800 − 900 = 900
=> FJ _|_ FL. Chứng minh tương tự ta cũng có: DJ _|_ DL
Ta có: FJ _|_ FL ; DJ _|_ DL và YJ _|_ YL (cmt) => 5 điểm J, F, L, D, Y cùng thuộc 1
đường tròn đường kính LJ => Tứ giác FJYD nội tiếp => 𝐹𝑌𝐽 ̂ = 𝐹𝐷𝐽 ̂
Mà JF = JD => Tam giác JFD cân tại J => 𝐹𝐷𝐽 ̂ = 𝐽𝐹𝑉 ̂ => 𝐹𝑌𝐽 ̂ = 𝐽𝐹𝑉 ̂ Xét ∆JYF và ∆JFV: 𝐹𝐽𝑆
̂ là góc chung ; 𝐹𝑌𝐽 ̂ = 𝐽𝐹𝑉 ̂(cmt) 𝐽𝑌 𝐽𝐹 𝐽𝑌 𝐽𝐵
=> ∆JYF ~ ∆JFV (g – g) => = . Mà JF = JB (cmt) => = 𝐽𝐹 𝐽𝑉 𝐽𝐵 𝐽𝑉 Xét ∆JYB và ∆JBV: 𝐽𝑌 𝐽𝐵 𝐵𝐽𝑉 ̂ là góc chung ; = (cmt) 𝐽𝐵 𝐽𝑉
=> ∆JYB ~ ∆JBV (c – g – c ) => 𝐽𝐵𝑉 ̂ = 𝐽𝑌𝐵 ̂ = 900 => BV _|_ BE
Mà AC _|_ BE (gt) => AC // BV => V là giao điểm của đường thẳng qua B song song với
AC với cạnh DF. Mà Q cũng là giao điểm của đường thẳng qua B song song với AC với cạnh DF
(gt) => Q trùng với V => BL _|_ PQ
Mà BL // OK (cmt) => OK _|_ PQ (đpcm) ĐỀ 8
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
I/ PHẦN TRẮC NGHIỆM:(5,0 điểm) Khoanh tròn vào chữ cái đầu câu mà em chọn
Câu 1: Cho hàm số y = 4x2. Điểm nào sau đây thuộc đồ thị hàm số B. (4; 32) B. (– 2; 16) C. (–2; – 16) D. Hai câu A, C đúng
Câu 2. Cho đều ABC nội tiếp đường tròn tâm O. Tiếp tuyến Ax (A là tiếp điểm; cung ABC là cung
chứa góc CAx) số đo góc ngoài CAx là: :
B. góc CAx = 300 B. góc CAx = 600 C. góc CAx = 900 D. góc CAx = 1200
Câu 3. Đồ thị hàm số nào đi qua gốc tọa độ O(0;0) C. y = 2x – 1 B. y = 2x C. y = 2x2
D. hai câu A, B đều đúng.
Câu 4: Góc có đỉnh nằm trong đường tròn thì bằng B.
Tổng số đo hai cung bị chắn.
C. Hiệu số đo hai cung bị chắn. D.
Nửa tổng số đo hai cung bị chắn.
D. Nửa hiệu số đo hai cung bị chắn.
Câu 5: Điểm A(–4; 4) thuộc đố thị hàm số y = ax2. Vậy a bằng 1 1 B. a = B. a = – C. a = 4 D. a = – 4 4 4
Câu 6. ABC nội tiếp đường tròn đường kính AB thì Trang 29 B. góc A = 900 B. góc C = 900 C. góc B = 900 D. ba câu A, B, C sai
Câu 7: Trong các hàm số sau, hàm số nào đồng biến khi x < 0?
A. y = -2x B. y = -x + 10 C. y = ( 3 - 2)x2 D. y = 3 x2
Câu 8: Tứ giác ABCD nội tiếp đường tròn có góc A = 400 ; góc B = 600 Khi đó góc C – góc D bằng A. 300 B . 200 C . 1200 D . 1400
Câu 9: Điểm A(-2; -1 ) thuộc đồ thị hàm số nào? 2 x 2 x 2 x 2 x A. y = B. y = - C. y = - D. y = 4 2 4 2
Câu 10: Phương trình x2 +x – 2 = 0 có nghiệm là:
A. x = 1 ; x = 2 B. x = -1 ; x = 2 C. x = 1 ; x = -2 D. Vô nghiệm
Câu 11: Với giá trị nào của a thì phương trình x2 + 2x – a = 0 có nghiệm kép
A. a = 1 B. a = 4 C . a = -1 D. a = - 4
Câu 12: Phương trình nào sau đây có hai nghiêm 3 và –2
A. x2 – x -2 = 0 B. x2 + x -2 = 0 C. x2 + x -6 = 0 D. x2 - x -6 = 0
Câu 13: Giá trị nào của m thì phương trình x2 – ( m+1)x + 2m = 0 có nghiệm là: 3 3 A. m = - B. m =
C. m = 2 D. Một đáp số khác 2 2
Hãy chọn từ thích hợp để điền vào chỗ trống trong các câu sau
Góc có đỉnh trùng với tâm đường tròn được gọi là…………………….
Số đo của nửa đường tròn bằng …………………
Hai cung được gọi là bằng nhau nếu chúng có số đo …………………
Trong hai cung , cung nào có số đo ………………… được gọi là cung lớn hơn
Góc nội tiếp chắn nửa đường tròn là ……………….
II/ Phần tự luận: (5,0điểm) 2x y
Câu 1 (0.5đ) Giải hệ phương trình 3 ;
x y 6 1
Câu 2 (1đ). a, Vẽ đồ thị hàm số 2 y x (P) 2
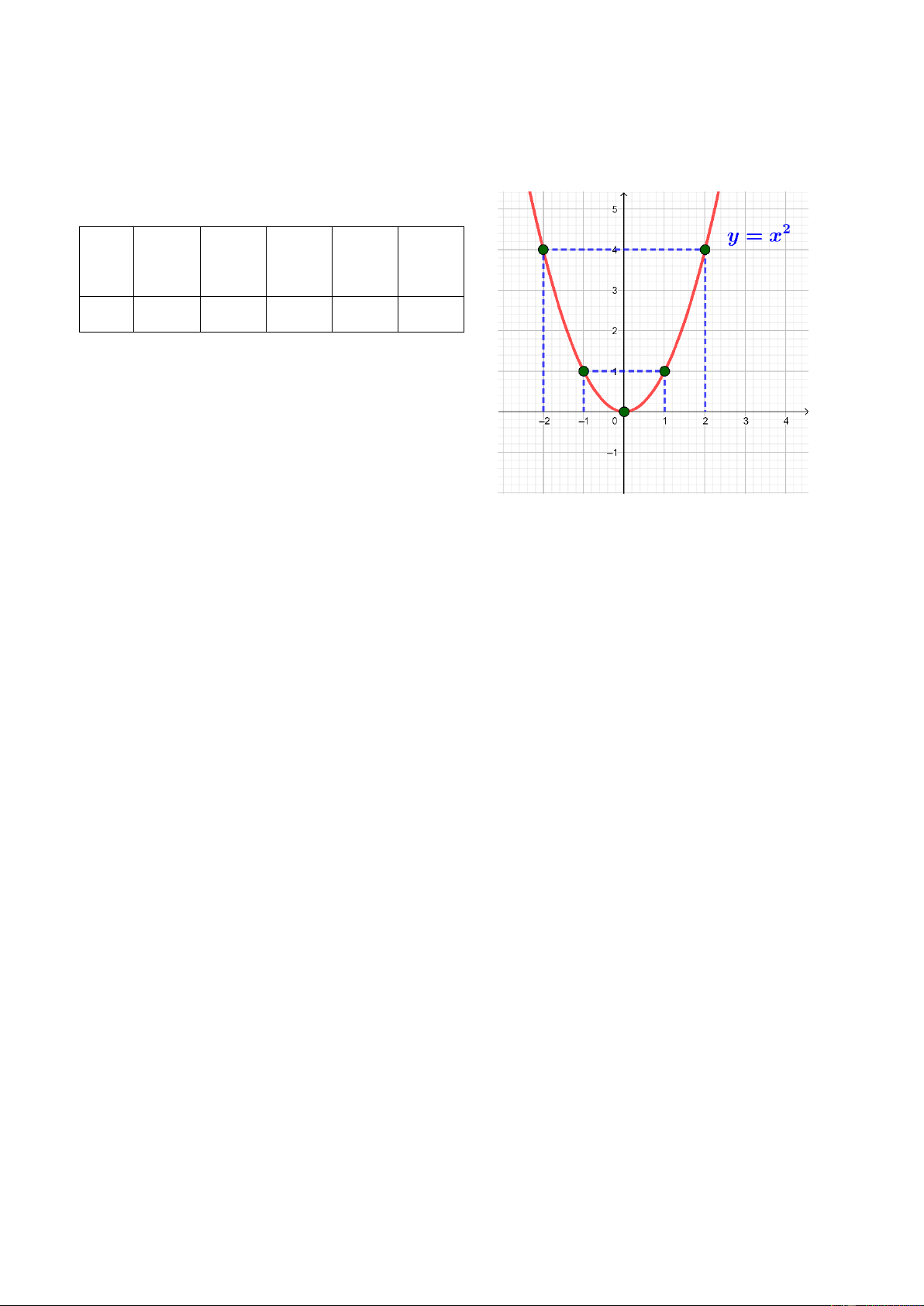
b, Tìm giá trị của m sao cho điểm C(-2; m) thuộc đồ thị (P)
Câu 3 (1.5 đ) Cho phương trình bậc hai x2 – (m + 1)x + m = 0 (1).
1. Giải phương trình (1) khi m = 3.
2. CMR: Phương trình (1) luôn có nghiệm với mọi m.
3. Trong trường hợp (1) có hai nghiệm phân biệt.Tìm hệ thức liên hệ giữa x1, x2 không phụ thuộc vào m.
Câu 4. (2.5đ). Cho đường tròn tâm O, đường kính BC, Lấy điểm A trên cung BC sao cho AB < AC .
Trên OC lấy điểm D, từ D kẻ đường thẳng vuông góc với BC cắt AC tại E .
a) Chứng minh : góc BAC = 900 và tứ giác ABDE nội tiếp?
b) Đường cao AH của tam giác ABC cắt đường tròn tại F. Chứng minh HF.DC = HC.ED?
c) Chứng minh BC là tia phân giác của góc ABF? 2
xy 4 8 y
Câu 5. (0,5đ) Giải hệ phương trình: 2
xy 2 x Đáp án: Câu
Nội dung – Đáp án Điểm
TRẮC NGHIỆM (mỗi câu 0,25 đ)
1-B ; 2-D ; 3-B ; 4-B ; 5-A ; 6-B; 7-C; 8-B 2,0
TỰ LUẬN (8 điểm) Câu 1 3𝑥 = 9 0,25 2x y c) 3 {
x y 6 𝑥 − 𝑦 = 6 0,25 𝑥 = 3 {𝑦 = −3 Trang 30
Vậy phương trình đã cho có nghiệm duy nhất là (x;y) = (3; -3)
3x 2y 2 3𝑥 − 2(2𝑥 − 1) = 2 d) { 0,25 2x y 1 𝑦 = 2𝑥 − 1 𝑥 = 0 { 0,25 𝑦 = −1
Vậy phương trình đã cho có nghiệm duy nhất là (x;y) = (0; -1)
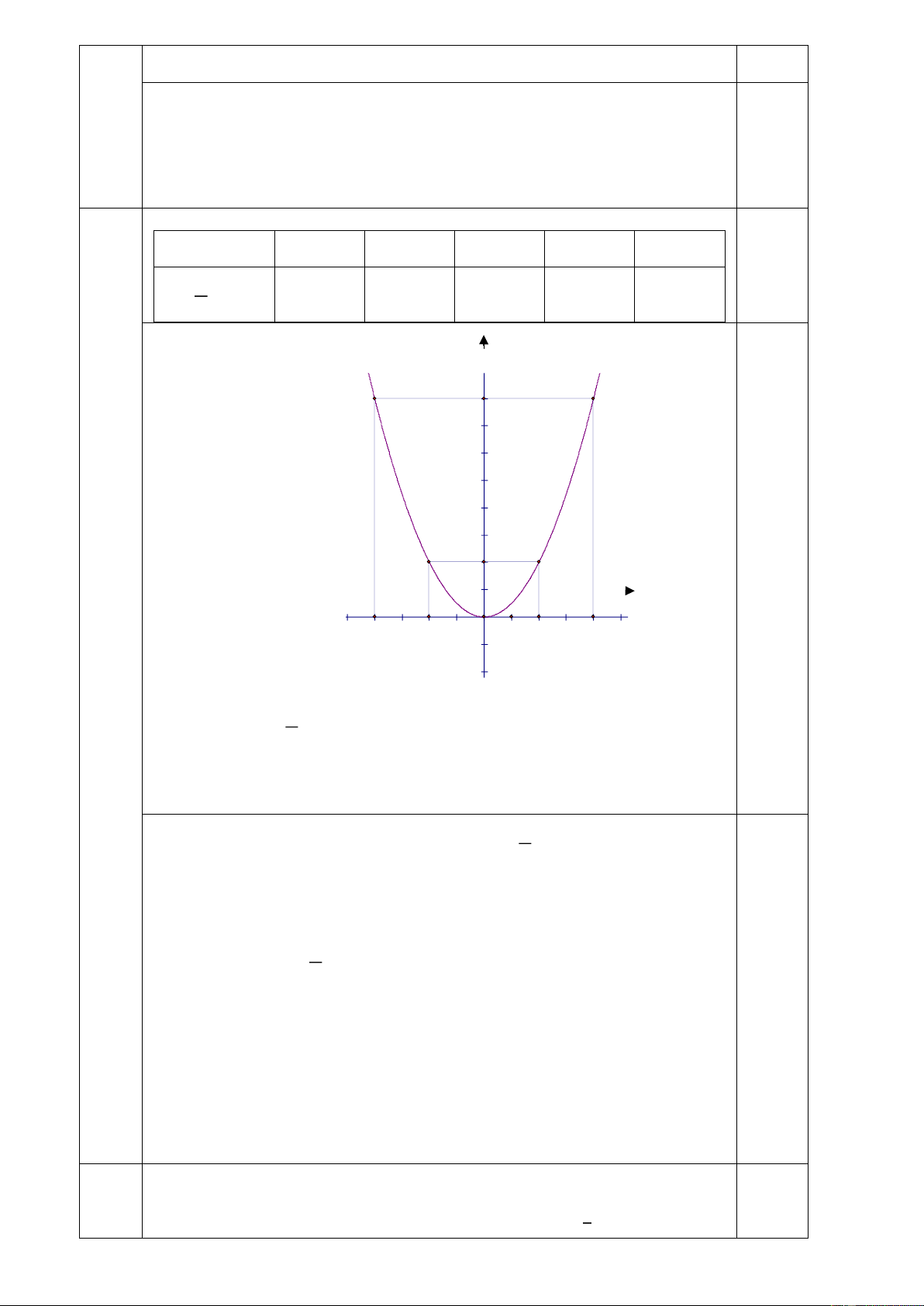
Câu 2 a)Lập bảng các giá trị -4 -2 2 4 1 2 0,25 y = x 8 2 0 2 8 2 10 y y 8 0,25 6 4 2 x x O -10 -5 -4 4 -2 2 5 10 -2 1 -4 Đồ thị hàm số y = 2
x là đường parabol có đỉnh là gốc toạ độ O, nhận trục 2
tung làm trục đối xứng, nằm phía trên trục hoành vì a >0 -6 1
b) Vì C (-2 ; m) thuộc parabol (p) nên ta có m = ( 2 2) m = 2 0, 5 2
Vậy với m = 2 thì điểm C ( -2; 2) thuộc parabol (p)
c, Hoành độ giao điểm của parabol (p) và đường thẳng y = x - 0,5 là nghiệm 0,25 1 của phương trình: 2 x = x - 0,5 2 2 x = 2x - 1 2 x - 2x + 1 = 0 2 (x 1) = 0 x - 1 = 0 x = 1 0,25
Thay x = 1 vào y = x - 0,5 ta được y = 0,5
Vậy tọa độ giao điểm là ( 1 ; 0,5) Câu 3
Gọi thời gian hai công nhân làm xong công việc nếu làm một mình lần lượt 0,25
là a và b (ngày) (a, b>0)
Nếu làm một mình trong 1 ngày người thứ nhất làm được 1 công việc. 𝑎 Trang 31
Người thứ hai làm được 1 công việc 𝑏
Hai công nhân cùng làm chung công việc hết 6 ngày xong nên ta có: 1 1 6. +6. = 1 (1) 𝑎 𝑏
Người thứ nhất làm 4 ngày rồi nghỉ, người thứ 2 làm tiếp 6 ngày thì hoàn
thành được 4545 công việc nên ta có: 0,25 1 1 4 4. +6. = (2) 𝑎 𝑏 5
Từ (1) và (2) ta có hệ phương trình: 1 1 6. + 6. = 1 0,25 { 𝑎 𝑏 1 1 4 4. + 6. = 𝑎 𝑏 5 1 1 = 𝑎 = 10 {𝑎 10 { 1 1 (thỏa mãn điều kiện) 0,25 = 𝑏 = 15 𝑏 15
Vậy nếu làm 1 mình thì người thứ nhất hoàn thành công việc trong 10 ngày,
người thứ hai hoàn thành công việc trong 15 ngày. 0,25 0,25 Câu 4 Vẽ hình đúng 0,5
d) Chỉ ra được góc BAC nội tiếp chắn nửa đường tròn. 0,5 Suy ra : góc BAC=900
Xét tứ giác ABDE có 𝐵𝐴𝐶 ̂ + 𝐵𝐷𝐸 ̂ = 1800 0,5
Suy ra tứ giác ABDE nội tiếp 0,75
e) – chứng minh được ∆𝐴𝐻𝐶 đồ𝑛𝑔 𝑑ạ𝑛𝑔 ∆𝐷𝐸𝐶 (𝑔. 𝑔) 0,5 -
Chứng minh được AH=HF .suy ra được HF.DC = HC.ED 0,5
f) Chứng minh được góc ABC= góc FBC.
Suy ra BC là tia phân giác của 0,25 góc ABF. Câu 5 2 2 x
Ta có: xy = 2 + x2 2 nên xy 0 và y
Thay giá trị này vào pt thứ x 0,25 2 2 2 2 nhất ta có: 2 x 2 x 2 x 2 8 . Do 2
x 2 0 nên 8 - 0 x x
( 2 + x2)2 8x2 x4 - 4x2 + 4 0 ( x2 - 2)2 0
( x2 - 2)2 = 0 ( vì ( x2 - 2)2 ) 0
x2 = 2 x 2; x 2
Nếu x 2 thì y 2 2 , Nếu x 2 thì y 2 2 , 0,25 1 1 2 2
Vậy hệ có hai nghiệm (x ; y) là ( 2 ; 2 2 ), ( 2 ; 2 2 )
Lưu ý: học sinh làm đúng cách khác vẫn được điểm tối đa. Trang 32 ĐỀ 9
ĐỀ KIỂM TRA HỌC KỲ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
Câu 1: (2,0 điểm )
1) Giải các phương trình : 2x2 - 5x + 3= 0
x 2y 1
2) Giảihệ phương trình sau
2x y 2 x 2 5 1
Câu 2: (2,0 điểm ) Cho biểu thức A = ( Với x>0 và x 4) x 3 x x 6 2 x 1) Rút gọn A
2) Tính giá trị của biểu thức A khi x = 3 - 2 2 1
Câu 3 (2.0 điểm): Trong mặt phẳng tọa độ Oxy cho parabol (P) : y = x2 và đường thẳng 2
(d) : y = 2x - m + 1 ( với m là tham số)
1) Tìm m để (d) đường thẳng đi qua điểm A(-1;3)
2) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có tọa độ (x1;y1) ;
(x2;y2) sao cho : x1x2(y1 + y2) +48 =0
Câu 4 (3 điểm): Cho đường tròn (O) đường kính AB .Vẽ tia tiếp tuyến Ax với đường tròn
(O) . trên tia Ax lấy điểm M bất kỳ khác A .Qua M vẽ cát tuyến MCD với (O) ( C nằm
giữa M và D ; C; D không cùng thuộc nửa mặt phẳng bờ AB .MO nằm giữa MA và MC )
kẻ OH vuông góc với CD tại H
1) Chứng minh tứ giác AOHM nội tiếp
2) Chứng minh: AM . AD = AC . DM
3) Tia MO cắt các tia BC và BD lần lượt ở I và K chứng minh AI = BK
Câu 5: (1,0 điểm): Cho x ; y là các số thực tùy ý . 2 2 x y 2 2 1 x y
Tìm giá trị lớn nhất của : A = 1 x 2 2 1 y 2 2
------------------------------------------HẾT------------------------------------------ ĐÁP ÁN Câu
Hướng dẫn chấm Điểm
Giải phương trình :2x2 - 5x + 3= 0Là phương trình bậc hai ẩn x
có dạng : a + b + c = 2+(-5) +3 = 0 phương trình có nghiệm x = 1 áp dụng vi 1 0,5 c 3 c 3 ét ta có x 2=
vậy phương trình có 2 nghiệm x1= 1;x2= 0,5 a 2 a 2 Câu1 3 x 2 y 1 2đ 1 2 y
x 2y 1
x 2y 1
x 2y 1 b) 0,25 3 5
2x y 2
4x 2y 4 5x 3 x 3 5 x 5 0,25 0,25 Trang 33 8 2y 5 x 3 5 4 y 4 y
5 vậy nghiệm của hệ là 5 3 x 3 x 5 5 x 2 5 1 x 2 5 1 1) Rút gọn A : A = A= x 3
x3 x 2 x 3 x x 6 2 x x 2
x 2 x 2 5 x 3 A = 0,25 x
3 x 2 x 3 x 2 x 2 x 3 x 3 x 3 x
x 9 x Câu2 x x 4 5 3 3 3 A = A = A = 2đ
x 3 x 2 x 3 x 2 x 3 x 2 0,5
x 3 1 x x x 3 3 1 4 A = A = = 0,25 x 3 x 2 x 2 x 2 2 2) x = 3 - 2 2 x= 2 2 2 2 1 . 1 x= 2 2 1 x = 2 1 0,25 2 5 2 2 1 4 2 5 3 2 3 2 5 2 15 Thay vào A ta có A = = = = 0,5 2 3 2 2 1 2 2 3 3 2 9 2 3 2 5 2 15 2 2 13 2 2 13 = 0,25 2 9 7 7
Câu3 1) (d) đi qua điểm A(-1;3) có tọa độ x= -1 ; y = 3 thay vào y = 2x - m + 1 ta có : 3 0,25 2
=2.(-1) – m + 1 m = -4 vậy với m = - 4 thì (d) đi qua A(-1;3) 0,25
2) phương trình hoành độ giao điểm của (d) và (P) là : 1 x2 = 2x - m + 1 2
x2 -4x +2m – 2 =0 a = 1 ; b = -4 ; c = 2m- 2 ; = b2- 4ac = 16-4.1.(2m-2) 0,25
= 16- 8m+8=24-8m để phương trình có hai nghiệm khi >0 hay 24-8m >0 b
Suy ra m< 3 theo vi ét ta có x 1 + x2 = 4 ; x1.x2 = 2m - 2 a 0,25 1 1 1 Mà x 2 2 1x2(y1 + y2) +48 =0 x1x2( x + x ) +48=0 x1x2( 2 x + 2 x ) +48 = 0 2 1 2 2 2 1 2 1 1 x 42 .2 2m2 x x
2x x +48 = 0 thay số ta có .(2m - 2 ) +48=0 1 2 2 1 2 1x2 2 2 .(m - 1 ) 42 .
2 2m 2+48=0 (m - 1) 16 4m 4 +48=0 (m - 1 ) 20 m 4
+48=0 (m - 1 ) 5 m 4
. +48=0 (m - 1 ) 5 m . + 12=0
5m -m2-5+ m +12 = 0 -m2 +6m +7 = 0 m2 - 6m -7 = 0 là phương trình bậc 0,25
hai ẩn m có dạng : a-b+c = 1-(-6)+ (-7) = 1+6 – 7 = 0 phương trình có nghiệm x1 c ( 7 ) =-1 áp dụng vi et ta có x =7 vậy x 2= = 1 = -1< 3( thõa mãn) a 1
( loại vì m<3 ; x = 7 ( loại vì không thõa mãn m<3) 2
Vậy m = -1 thì đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có tọa độ 0,25
(x1;y1) ; (x2;y2) sao cho : x1x2(y1 + y2) +48 =0 Trang 34
1) Chứng minh tứ giác AOHM nội tiếp K
Vì Ax là tiếp tuyến mà MAx nên MA AO Câu4 Hay O A M ˆ
= 900 mà OH CD tại H (gt) 0,25 3đ nên O H M ˆ = 900 suy ra O A M ˆ + O H M ˆ =1800 0,25 D vì O A M ˆ và O H
M ˆ là hai góc đối của tứ giác AOHM 0,25 1
nên tứ giác AOHM nội tiếp 0,25 O A B
2) Chứng minh: AM . AD = AC . DM N
Xét MDAvà AD có góc D chung F H 0,25 Sđ 1 M A C ˆ
= sđ AC (góc giưa tia t/ tuyến và 1dây) 2 Sđ 1 0,25 C D A ˆ
= sđ AC ( nội tiếp chắn AC) C I 2 1 nên M A C ˆ = C D A ˆ Vậy MDA ADC(g-g) 0,25 AC AM M
AC.DM=AD.AM(đ/ phải h/minh) AD DM 0,25 3) chứng minh AI = BK
Qua D kể đường thẳng // OM cắt AB ở N và cắt BC ở F ta có ˆD M O ˆ F D M ( so le trong) (1)
Ta có tứ giá AOHM nội tiếp ˆH A O ˆ H M O vì ˆD M O ˆ H M O nên ˆH A O ˆ D M O (2) 0,25
Từ (1) và (2) suy ra ˆH A O ˆ F D M ( = D M O ˆ ) hay ˆH A N ˆ N D H suy ra t/g AHND n/tiếp Nên ˆD A N ˆ D H N
( cùng chắn cung ND) vì ˆD A N ˆ D A B hay ˆD A B ˆ D H N (3) . xét (O) ta có ˆ D A B ˆ D C B ( cùng chắn cung BD) (4) từ (3) và (4) suy ra ˆ 0,25 D H N ˆ D C B ( = D C
B ˆ ) suy ra NH // BC ( đồng vị)
Xét CDF ta có NH//CF và HC = HD (đường kính vuông góc với một dây)
ND = NF N là trung điểm của FD Áp dụng định lý ta let cho BOI và NF BN NF ND BOK ta có OI BO 0,25 ND BN IO OK OK BO
mà NF = ND OI =OK .Xét tứ giác AIBK ta có OB=OA=Rvà OI=OK nên
tứ giác AIBK là hình bình hành suy ra AI = BK 0,25 Câu5 2 2 x y 2 2 . 1 x y
1điểm Cho x;y R Tìm giá trị lớn nhất của : A = 1 x 2 2 1 y 2 2
a b1 ab
Đặt x2 = a ; y2 = b ( a>0; b>0) ta có A = 0,25
1 a2 1 b2 0,25
Ta có ( a-b)(1-ab) = a-a2b – b +ab2 a +ab2 = a.(1+b2) ( a-b)(1-ab a.(1+b)2 a . 1 b2 Mặt khác ta có ( 1+a)2 1
= (1-a)2 +4a 4ª suy ra A = dấu = sảy ra khi 0,25 4a1 b2 4 1
a=1 ; b = 0 x= 1 ; y=0 vậy Max A = khi x= 1 ; y=0 0,25 4 Trang 35 K D 1 O A B N F H C I 1 M Trang 36




