Đề thi tuyển sinh toán 10 chuyên tin Quảng Nam 2021-2022 (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM NĂM HỌC 2021-2022
Môn thi: TOÁN (Chuyên Tin) ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
Khóa thi ngày: 03-05/6/2021 Câu 1. (1,5 điểm) Cho biểu thức 1 1 4 P   
(với x  0, x  4 ) . x  2 x  2 x  4
Rút gọn biểu thức P và tìm tất cả các giá trị của x sao cho P = 1. Câu 2. (1,0 điểm) Cho phương trình 4 3 2
x  7x  (m  2)x  2021x  m  0 (*) , với m là tham số nguyên.
Chứng minh rằng x 1 không phải là nghiệm của phương trình (*) và phương trình
này có không quá một nghiệm nguyên. Câu 3. (1,0 điểm) Cho parabol 2
(P) : y  x và đường thẳng (d) : y  2x  m (m là tham số). Tìm m để
đường thẳng (d) cắt (P) tại hai điểm phân biệt A x ; y , B x ; y thỏa mãn 1 1   2 2
x x  y y  6. 1 2 1 2 Câu 4. (2,0 điểm)
a) Giải phương trình x  2  2x 1. 2 2
x  y  3
b) Giải hệ phương trình  . 2
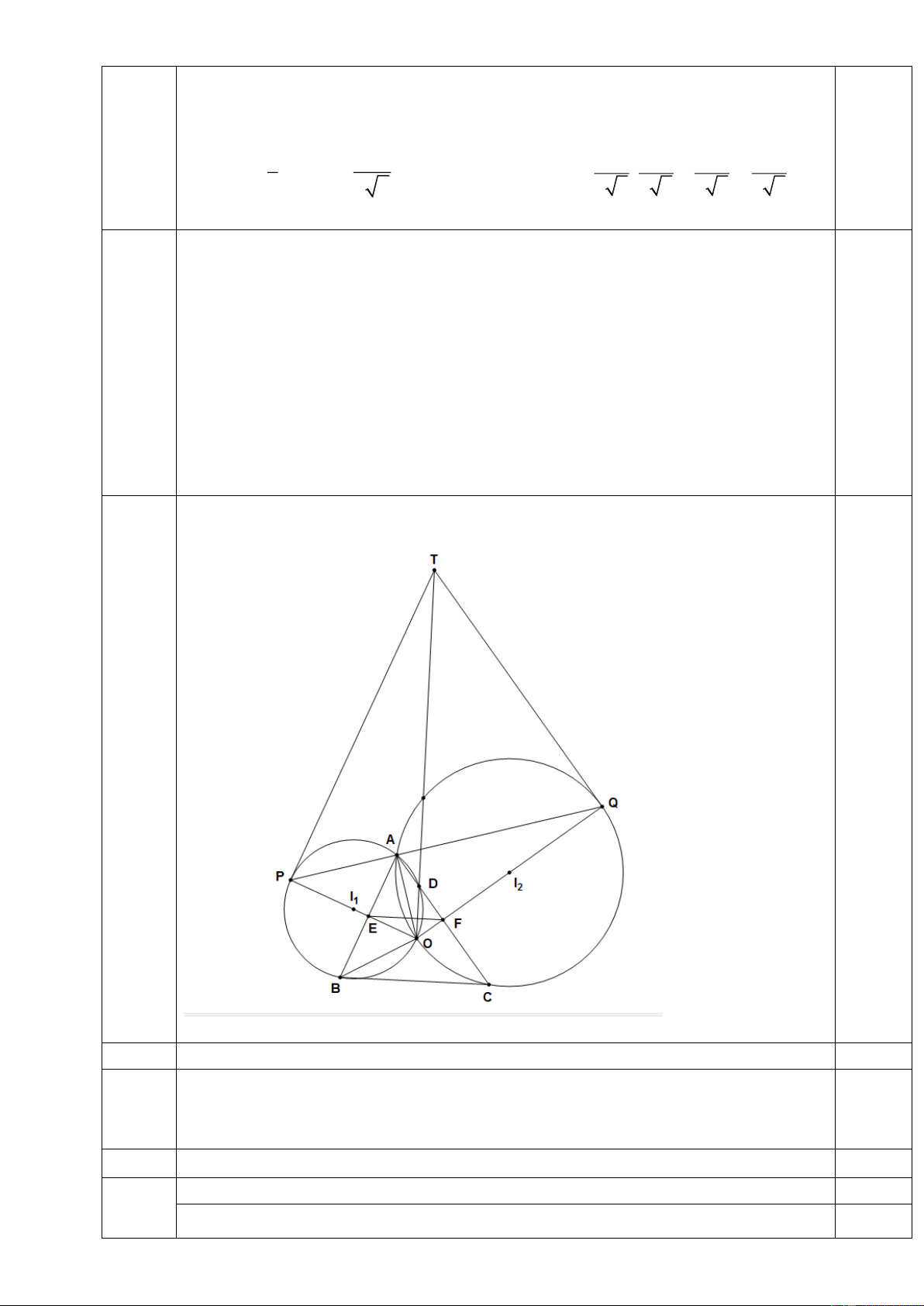
xy  3y  1  Câu 5. (3,5 điểm)
Cho tam giác nhọn ABC (AB < AC) có E, F lần lượt là trung điểm của AB và AC.
Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Gọi  1
I  là đường tròn ngoại
tiếp tam giác ABO và I2  là đường tròn ngoại tiếp tam giác ACO. Kẻ các đường kính OP của  1
I  và OQ của I2  .
a) Chứng minh tứ giác AEOF nội tiếp đường tròn.
b) Chứng minh hai tam giác OEF và OQP đồng dạng.
c) Cạnh AC cắt đường tròn  1
I  tại D (D khác A). Tiếp tuyến của  1 I  tại P và tiếp
tuyến của I2  tại Q cắt nhau tại T. Chứng minh ba điểm O, D, T thẳng hàng. Câu 6. (1,0 điểm)
Cho ba số thực dương a,b,c thỏa mãn 1 1 1
a  b  c 
   Tìm giá trị nhỏ nhất a b c
của biểu thức P  ab  bc  c . a
--------------- HẾT ---------------
Họ và tên thí sinh:............................................................................................. Số báo danh: ......................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM NĂM HỌC 2021-2022 HDC CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN CHUYÊN TIN
(Bản hướng dẫn này gồm 04 trang) * Lưu ý:
Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm
từng phần như hướng dẫn quy định. Câu Nội Dung Điểm 1 1 4 Cho biểu thức P   
(với x  0, x  4 ) . 1,5 x  2 x  2 x  4
Rút gọn biểu thức P và tìm tất cả các giá trị của
x sao cho P = 1. Tính được 1 1 2 x   0,25 x  2 x  2 x  4 2 x  4 Suy ra P  x  4 0,25 Câu 1 2  x  2   0,25
x  2 x  2 Kết quả: 2 P  x  2 0,25 2 P  1 
 1 x  0, x  4 0,25 x  2     x 4 x 16. 0,25 Cho phương trình 4 3 2
x  7x  (m  2)x  2021x  m  0 (*) , với m là tham
số nguyên. Chứng minh rằng x 1 không phải là nghiệm của phương trình 1,0
(*) và phương trình này có không quá một nghiệm nguyên. Đặt 4 3 2
f (x)  x  7x  (2  m)x  2021x  m
Tính f (1)  2m  2025 0,25
Vì m là số nguyên nên f (1)  2m  2025  0
Vậy x 1không phải là nghiệm của phương trình (*). 0,25 Câu 2 Giả sử 
x là nghiệm nguyên của phương trình (*), ta có f (x ) 0 0 0 Khi đ
ó f (x )  f (1)  2
 m  2025 chia hết cho x 1, suy ra ( x 1) là số 0 0 0
lẻ, suy ra x là số chẵn. 0,25 0
Giả sử PT (*) có 2 nghiệm nguyên phân biệt x , x 1 2 Suy ra: x , x
f (x )  f (x )  0 . 1 2 là các số chẵn và 1 2
Ta có f (x )  f (x )  0 1 2 3 2 2 2 2 2
 (x  x x  x x  x )  7(x  x x  x )  (m  2)(x  x )  2021  0 x  x 1 1 2 1 2 2 1 1 2 2 1 2  1 2 Trang 2
Do vế trái là số lẻ nên mâu thuẩn. Vậy bài toán được chứng minh. 0,25 Cho parabol 2
(P) : y  x và đường thẳng (d) : y  2x  m (m là tham số).
Tìm m để đường thẳng (d) cắt (P) tại hai điểm phân biệt 1,0
A x ; y , B x ; y thỏa mãn x x  y y  6. 1 1   2 2 1 2 1 2
Phương trình hoành độ giao điểm của P và d là 2
x  2x  m Hay 2
x  2x  m  0 (1) 0,25
Tính được ' 1 m và suy ra được '  0  m  1  0,25
Câu 3 Theo hệ thức Viet x x  m 1 2 Ta có:
x x  y y  6 1 2 1 2 2 
x x  ( x x )  6 1 2 1 2 0,25 2
 m  m  6  0 m  3   m  2
So điều kiện, suy ra m=3. 0,25
a) Giải phương trình x  2  2x 1. 1,0 2x 1  0
x  2  2x 1   2
x  2  (2x 1) 0,25  1 x     2 Câu 4 2
4x  3x 1 0 (*) 0,25 ( 2,0 )
Giải PT (*) ta được x  1  hoặc 1 x  4 0,25
So điều kiện, kết luận 1 x  . 0,25 4
( HS có thể bình phương rồi thử lại). 2 2
x  y  3 (1)
b) Giải hệ phương trình  . 1,0 2
xy  3y  1  (2) 2 Nhận thấy 3y  1
y  0 không phải là nghiệm của (2) nên rút x  y 0,25 2 2  3y 1
Thay vào phương trình (1) được: 2  y  3    y  Đưa về phương trình: 1 4 2 2 2
8 y  9 y  1  0  y  1, y  8 0,25 Trang 3 Với 2
y  1  x  2  , suy ra hai nghiệm ( 2  ; 1  ),(2;1) . 0,25 Với 1 5 2 y   x   , suy ra hai nghiệm 5 1 5 1 ( ; ),( ;  ) . 0,25 8 2 2 2 2 2 2 2 2 2 2
( Không lí luận y  0 thì trừ
0,25 và chấm tiếp)
Cho tam giác nhọn ABC (AB < AC) có E, F lần lượt là trung điểm của AB
và AC. Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Gọi
 1I là đường tròn ngoại tiếp tam giác ABO và I2 là đường tròn ngoại
tiếp tam giác ACO. Kẻ các đường kính OP của  1
I  và OQ của I2  Câu 5
a) Chứng minh tứ giác AEOF nội tiếp đường tròn. 3.5
b) Chứng minh hai tam giác OEF và OQP đồng dạng.
c) Cạnh AC cắt đường tròn  1
I  tại D (D khác A). Tiếp tuyến của
 1I tại P và tiếp tuyến của I2 tại Q cắt nhau tại T. Chứng minh ba
điểm O, D, T thẳng hàng. 5a
a. Chứng minh tứ giác AEOF nội tiếp trong đường tròn. 1,0
Hình vẽ phục vụ câu a. 0,25
Nêu được OE  AB, OF  AC (mỗi ý cho 0,25) 0,5
Suy ra tứ giác AEOF nội tiếp. 0,25 5b
b. Chứng minh O
 FE đồng dạng với OPQ  . 1,5 Hình vẽ 0,25 Ta có 0 0 0
OAP  OAQ  90  90  180 . Suy ra 3 điểm P, A, Q thẳng hàng. Trang 4 0,25 Xét hai tam giác O  FE và OPQ  có: Góc O chung (1) 0,25 OFE  OAE  ABO 0,25 QPO  APO  ABO 0,25 Suy ra OFE  QPO (2)
Từ (1) và (2) suy ra hai tam giác O  FE và OPQ  đồng dạng. 0,25
Cạnh AC cắt đường tròn  1
I  tại D (D khác A). Tiếp tuyến của  1 I  tại P và
tiếp tuyến của I 1,0
2  tại Q cắt nhau tại T. Chứng minh O, D, T thẳng hàng. Lập luận: 0 0      0,25 5c DOQ DOF 90 FDO 90 ABO (1)
TOQ  TPQ (Tứ giác TPOQ nội tiếp) 0,25 0 0
 PAB  90  APO90  ABO (2) 0,25
Từ (1) và (2) suy ra TOQ  DOQ và kết luận O, D, T thẳng hàng. 0,25
Cho các số thực dương a,b, c thỏa mãn 1 1 1
a  b  c    . Câu 6 a b c 1,0
Tìm giá trị nhỏ nhất của biểu thức P  ab  bc  ca . Cách 1: 1 1 1 2 abc(   ) 1 1 1 Có     (   ) a b c P ab bc ca abc  a b c
a  b  c 0,25 1 1 1 1 1 1 abc( 
 )  2(a b c) abc(   ) 2 2 2 2 2 2 a b c a b c    2 0,25
a  b  c
a  b  c 1 1 1 abc(   ) ab bc ca   2  1 2  3 .
a  b  c 0,25
Dấu bằng xảy ra khi a  b  c 1. Vậy Min P=3. 0,25 Cách 2: Biến đổi giả thiết 1 1 1 2 2 2
a  b  c 
   a bc  b ac  c ab  ab  bc  ca  P 0,25 a b c 2
CM được BĐT x  y  z  3xy  yz  zx 0,25
Áp dụng: x  a ,
b y  bc, z  ca thu được 2
P  3P  P  3 P  0 0,25
Dấu bằng xảy ra khi a=b=c=1. Vậy Min P=3. 0,25 Trang 5