Đề Thi Tuyển Sinh 10 Toán Chất Lượng Cao Sở GD Hòa Bình 2025-2026 Có Đáp Án

SỞ GD&ĐT HÒA BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG ĐỀ THI MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho thí sinh dự thi vào lớp Chất lượng cao) THUC
Thời gian làm bài: 150 phút, không kể thời gian giao đề.
Đề thi có 01 trang, gồm 04 câu.
-----------------------------------------------------------------------------------------------------------------------
Câu I (3,0 điểm)
1. Rút gọn các biểu thức: 5 − 5 a) A = 20 − b) 2
B = 4(x −1) với x  1. 5 −1 2. Giải phương trình: 4 2
(2x +1) − (2x +1) = 12
3. Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) : y = (m +1)x + 3 . Tìm giá trị của
m để đường thẳng (d) cắt đường thẳng (d ') : y = x + 2 tại một điểm có hoành độ bằng −1.
Câu II (3,0 điểm) 2
x − 5y + 5xy =1
1. Giải hệ phương trình:  2 2
x + y + x + 6y = −3 2. Cho phương trình: 2 2
x − 2mx + m − 4m + 4 = 0 (m là tham số). Tìm giá trị của m
để phương trình có hai nghiệm x ; x thỏa mãn: 2 2
x + x = x + x 1 2 1 2 1 2 .
3. Nhà bác Nga có mảnh vườn hình chữ nhật với diện tích 2
300 m . Nếu giảm chiều
dài đi 5m thì mảnh vườn đó trở thành hình vuông. Tính chu vi mảnh vườn hình chữ nhật ban đầu của bác Nga.
Câu III (3,0 điểm)
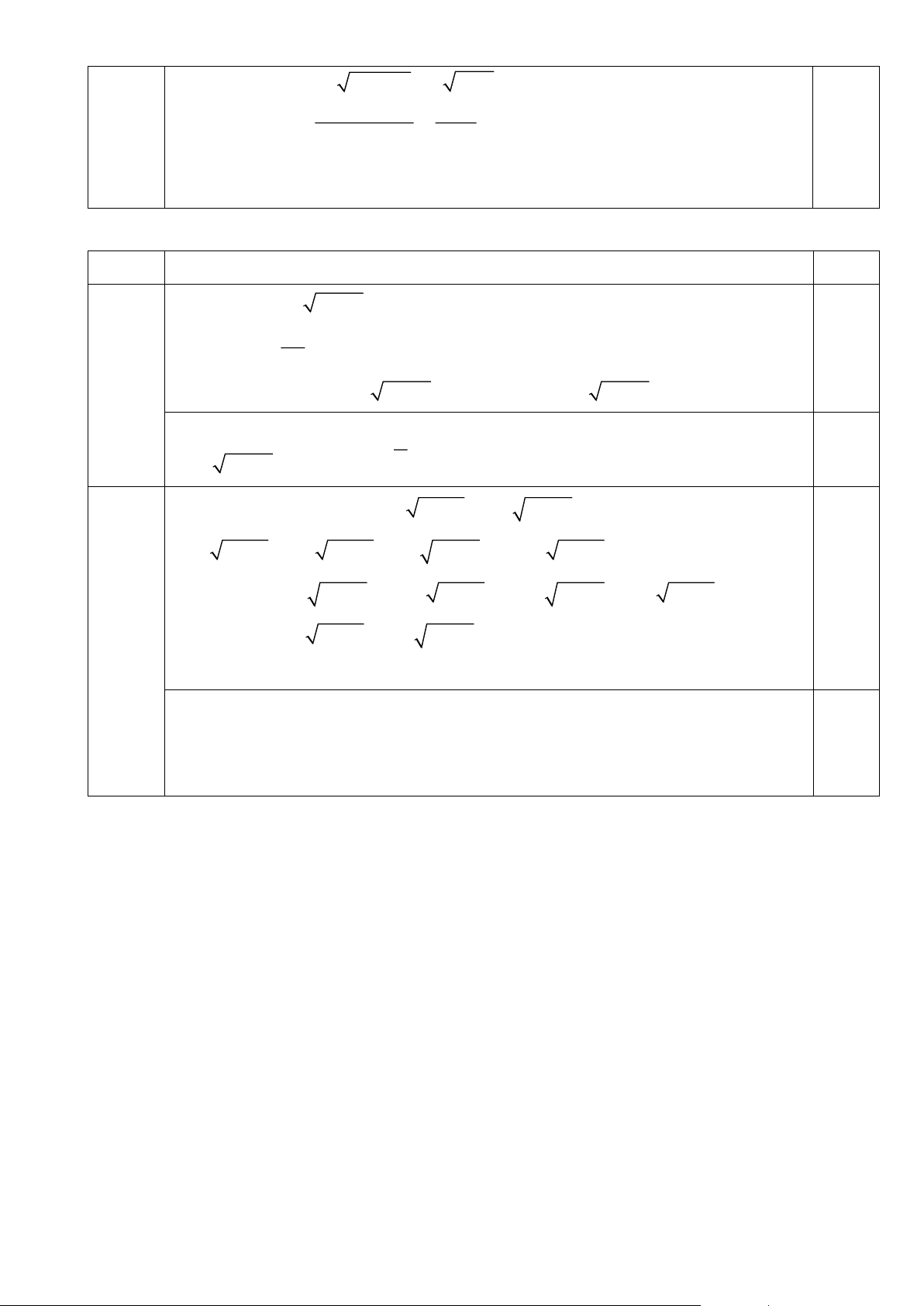
Cho đường tròn (O; R) đường kính AB cố định, C là điểm bất kỳ trên đường tròn
(C khác A và B) . Kẻ đường kính CD của đường tròn (O). Các đường thẳng AC, AD cắt
tiếp tuyến tại B của đường tròn (O) lần lượt tại E và F.
a) Chứng minh tứ giác CDFE nội tiếp được trong một đường tròn. b) Chứng minh 2 C . A CE + D . A DF = 4R .
c) Gọi S, S , S ° ° ° 1
2 theo thứ tự là diện tích của
AEF , BCE và BDF .
Chứng minh: S + S = S . 1 2
d) Xác định vị trí của điểm C để tứ giác CDFE có diện tích nhỏ nhất.
Câu IV (1,0 điểm) 1. Giải phương trình: 2
2x − 5x + 7 = 2 2x +1
2. Cho x, y là hai số thực thỏa mãn điều kiện ( 2 x + x + )( 2 1 y + y +1) =1.
Tìm giá trị nhỏ nhất của biểu thức: 4 4 2
P = 3x − 2y + 2xy − 2y + 4x + 8y + 2023 .
-------- HẾT --------
Họ và tên thí sinh:........................................... Số báo danh: ......................... Phòng thi: .....
Giám thị 1:.......................................................Giám thị 2:..................................................... Trang 1
SỞ GD&ĐT HÒA BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
HƯỚNG DẪN CHẤM MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho thí sinh dự thi vào lớp Chất lượng cao) THUC
Hướng dẫn chấm có 03 trang
Câu I (2,0 điểm) Phần Nội dung Điểm 5 − 5 5( 5 −1) A = 20 − = 2 5 −
= 2 5 − 5 = 5 0,5 1 5 −1 5 −1 2
B = 4(x −1) = 2 x −1 = 2x − 2 (vì x  1). 0,5 + 4 2
(2x +1) − (2x +1) = 12 Đặt: 2
(2x +1) = t (t  0) , ta được phương trình: 0,5 t  = 4 2
t − t −12 = 0  t   = −3 (KTM ) 2  1 = 2 +1 = 2 x x  2 2
t = 4  (2x +1) = 4     . KL: ... 0,5 2x +1 = −2 3 x = −  2
Đường thẳng (d ) cắt đường thẳng (d ') : y = x + 2 tại một điểm có hoành độ 0,5 3
bằng –1  Tọa độ giao điểm là M (−1;1) .
(d ) đi qua điểm M (−1;1)  −1.(m +1) + 3 = 1  m = 1. 0,5
Câu II(2,0 điểm) Phần Nội dung Điểm x =1 2
x − 5y + 5xy = 1 (
 x −1)(x +1+ 5y) = 0    
 x = −5y −1 0,5 2 2 2 2
x + y + x + 6y = −3
x + y + x + 6y = −3  2 2
x + y + x + 6y = −3 x = 1  x = 1 x = 1 y = −1 1       0,25 2 2 2  + + + = −  + + =  x y x 6y 3 y 6y 5 0 x = 1  y = −5
x = −5y −1
x = −5y −1     2 2 2
x + y + x + 6y = −3 2
 6y +11y + 3 = 0 (Vo nghie ) m 0,25
Vậy hệ phương trình đã cho có các nghiệm là: (1;−1); (1;−5).
Ta có:  ' = 4m − 4 . 0,5
Để phương trình có hai nghiệm phân biệt thì  ' = 4m − 4  0  m  1
x + x = 2m 2
Theo hệ thức Viét ta có: 1 2  2
x .x = m − 4m + 4 1 2 0,25 Do đó 2 2 2
x + x = x + x  (x + x ) − 2x x = x + x 1 2 1 2 1 2 1 2 1 2 2 2
 (2m) − 2(m − 4m + 4) = 2m m =1 (TM ) Từ (1) 2
 m + 3m − 4 = 0   . KL: … 0,25
m = −4 (KTM )
thuvienhoclieu.com Trang 2
Gọi chiều dài của mảnh vườn là x(m) . ĐK x  5. 300
Chiều rộng của mảnh vườn là (m) x 0,5
Nếu giảm chiều dài đi 5m thì mảnh vườn trở thành hình vuông nên ta có 3 300 phương trình: 2 x − 5 =
 x − 5x − 300 = 0 x
Giải phương trình ta được x = 20 (TM ); x = −15 (KTM ) 1 2
Vậy mảnh vườn có chiều dài là 20m , chiều rộng là 15m . 0,5
Chu vi mảnh vườn nhà bác Nga là: (20 +1 ) 5 .2 = 70m .
Câu III (3,0 điểm) Phần Nội dung Điểm
Ta có: ADC = ABC (hai góc nội tiếp cùng chắn cung AC) . 0,5 a
ABC = AEB (cùng phụ với BAE )
 ADC = AEB  CDFE nội tiếp được đường tròn. 0,5
Áp dụng hệ thức lượng trong ° ABE vuông tại B ta có: 2 BC = C . A CE 0,5 Tương tự: 2 BD = D . A DF b
Áp dụng định lí Pytago trong tam giác BCD vuông tại B ta có: 2 2 2 2
BC + BD = CD = 4R ; 0,5 2 2 2  C . A CE + D .
A DF = BC + BD = 4R 2 S EB S EB
Vì BC // AF nên ∆BCE ~ ∆FAE 1  = 1  = . 0,25 2 S EF S EF c S BF S S EB FB Tương tự ta có 2 = . 1 2  + = + =1 S EF S S EF EF 0,25 S + S = S 1 2 . 1 1 1 1 S = S − S = R EF − AC AD = R BE + BF − AC AD CDFE AEF ACD .2 . . .2 .( ) . 2 2 2 2 d 0,25 1 = .
R (BE + BF ) − AC.AD 2 Trang 3 Ta có: 2
BE + BF  2 BE.BF = 2 AB = 4R 2 2 2 AC + AD CD 2 AC.AD  = = 2R 2 2 0,25 AC = AD 2  s  R   ^ CDFE 3 . Dấu "=" xảy ra  CD AB . BE = BF
Câu IV (1,0 điểm) Phần Nội dung Điểm 2
2x − 5x + 7 = 2 2x +1 (1) −1 ĐKXĐ: x  0,25 2 1 2 2 2
(1)  4x −10x +14 − 4 2x +1 = 0  (2x − 3) + ( 2x +1 − 2) = 0 2x − 3 = 0 3    x = (TM ) . KL: ... 0,25  2x +1 − 2 = 0 2
Biến đổi giả thiết ta có: ( 2 x + x + )( 2 1 y + y +1) =1  ( 2 x + + x)( 2 x + − x)( 2 y + + y) = ( 2 1 1 1 x +1 − x)  ( 2 2 x + − x )( 2 y + + y) 2 2 2 1 1
= x +1 − x  y +1 + y = x +1 − x (1) 0,25 2 Tương tự, ta có 2 2
x +1 + x = y +1 − y (2)
Cộng theo vế các đẳng thức (1),(2) và rút gọn ta được y = −x . Ta có 4 4 2 2 4
P = 3x − 2x + 2x − 2x + 4x − 8x + 2023 = x − 4x + 2023 = ( 2 x − 2x + )
1 + 2(x − 2x + ) 1 + 2023 = (x − )2 1 + 2(x − )2 4 2 2 1 + 2026  2026 . 0,25
Vậy min P = 2026 khi và chi khi x = 1 và y = −1.
* Chú ý: Mọi cách giải khác đúng đều được xem xét và cho điểm tối đa.
-------- HẾT -------- Trang 4