Đề Thi Tuyển Sinh 10 Toán Chất Lượng Cao Sở GD Hòa Bình 2025-2026 Có Đáp Án

SỞ GD&ĐT HOÀ BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 TRƯỜNG PT DTNT THPT TỈNH ĐỀ THI MÔN TOÁN ĐỀ CHÍ NH THỨC (DÀNH CHO TH
Í SINH THI LỚP CHẤT LƯỢNG CAO TOÁN)
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
(Đề thi gồm có 01 trang, 04 câu)
Câu I (3,0 điểm)
1) Rút gọn các biểu thức:
a) A = 27 − 2 3
b) B = 6 + 2 5 − 5
2) Giải phương trình: 2x −1 = x + 6
3) Tìm a và b để đồ thị hàm số y = ax + b đi qua điểm M (1;3) và N (2;2) .
Câu II (3,0 điểm)
1) Cho đường thẳng (d): y = 5x − 2 và parabol (P): 2
y = 2x . Tìm tọa độ giao
điểm của (d) và (P).
2) Giải phương trình: x +1 = x −1
3) Hai chị em Hiền và Thảo đi mua ba lô và cặp sách chuẩn bị cho năm học
mới. Tổng giá niêm yết cho 1 chiếc ba lô và 1 chiếc cặp sách là 220000 đồng nhưng
cửa hàng đang có chương trình giảm giá 10% cho ba lô và 20% cho cặp sách nên hai
chị em phải trả tổng cộng 186000 đồng cho 1 chiếc ba lô và 1 chiếc cặp sách. Hỏi giá
niêm yết của 1 chiếc ba lô và 1 chiếc cặp sách là bao nhiêu?
Câu III (3,0 điểm).
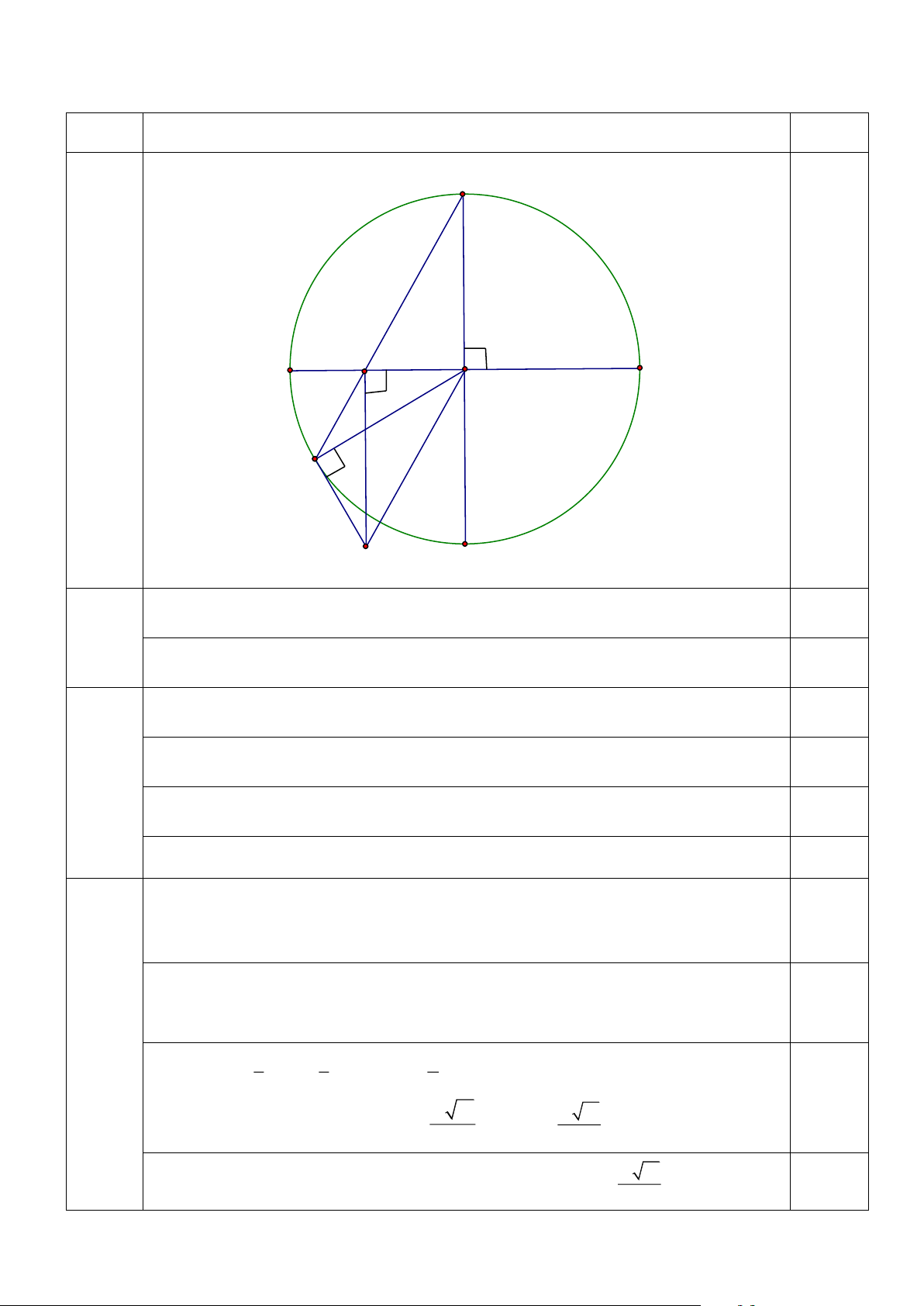
Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc với nhau. Trên
đoạn thẳng AO lấy điểm M (M khác A và O). Tia CM cắt đường tròn (O; R) tại điểm
thứ hai là N. Đường thẳng vuông góc với AB tại điểm M cắt tiếp tuyến tại N của
đường tròn (O; R) ở điểm P.
1) Chứng minh rằng: OMNP là tứ giác nội tiếp.
2) Chứng minh rằng: CN song song OP. 1
3) Khi AM = AO, tính bán kính của đường tròn ngoại tiếp tam giác OMN 3 theo R.
Câu IV (1,0 điểm).
1) Cho các số thực a, b, c thoả mãn: 2 2 2 3 3 3
a + b + c = a + b + c = 1.
Tính giá trị biểu thức: 2021 2022 2023 S = a + b + c
x + y + z = 6
2) Cho các số thực x, y, z thỏa mãn: 
. Chứng minh rằng z = 2 .
xy + yz + zx =12 -------- Hết --------
Họ và tên thí sinh: ............................................. Số báo danh: ......................... Phòng thi: .......
Giám thị 1 (Họ và tên): ...................................... Giám thị 2 (Họ và tên): ................................ Trang 0 SỞ GD & ĐT HOÀ BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10
TRƯỜNG PT DTNT THPT TỈNH
HƯỚNG DẪN CHẤM MÔN TOÁN CLC
(Hướng dẫn chấm này gồm có 03 trang)
Câu I (2,0 điểm) Phần, Nội dung Điểm ý
A = 3 3 − 2 3 = 3 0,5 1 2
B = (1+ 5) − 5 = 1+ 5 − 5 = 1 0,5 1
Nếu x  thì phương trình có dạng: 2x −1 = x + 6  x = 7 (TM ) 0,5 2 2 1 5 −
Nếu x  thì phương trình có dạng: 2
− x +1= x + 6  x = (TM ) 2 3 0,5 KL……. ìï a + b =
Vì đường thẳng (d): y = ax + b đi qua điểm M (1;3) N (2;2) 3 , ï Þ í 0,5 3 ï 2a + b = 2 ïî
Giải hệ phương trình ta được: a = - 1; b = 4 . 0,5
Câu II(2,0 điểm) Phần, Nội dung Điểm ý
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình: x = 2 2 2 2x 5x 2 2x 5x 2 0  = −  − + =  0,5 1 . 1 x =  2  1 1
Suy ra tọa độ giao điểm của (d) và (P) là:  (2;8), ; .   0,5  2 2  ĐKXĐ: x ³ - 1 0,25 2 + = −  + = −  x 1 x 1
x 1 (x 1) ,(DK x 1) 0,5 2 2  x − 3x = 0 x = 0(KTM )   . KL............ 0,25 x = 3(TM )
Gọi giá niêm yết một chiếc ba lô và một chiếc cặp sách lần lượt là x, y (đồng), 0,25 * x, y 
Theo bài ra ta có hệ phương trình: 3
x + y = 220000 x =100000    (TM ) 0,5 0
 ,9x + 0,8y =186000 y =120000
Vậy giá niêm yết một chiếc ba lô và một chiếc cặp sách lần lượt là 100000 0,25 đồng, 120000 đồng. Trang 1
Câu III (3,0 điểm) Phần Nội dung Điểm C M O A B N P D Có 0 OMP = 90 (gt); 0
ONP = 90 (tính chất tiếp tuyến) 0,5 1 Do đó OMP = 0
ONP = 90  OMNP là tứ giác nội tiếp 0,5
Do OMNP là tứ giác nội tiếp  ONC = OPM (cùng chắn OM ) 0,25
Ta có: MP // CD (cùng vuông góc với AB)  = (so le trong) 0,25 2 OPM POD
Mà tam giác OCN cân tại O  ONC = OCN 0,25  OCN = POD  CN // OP 0,25 Do OMP = 0
ONP = 90 nên đường tròn ngoại tiếp tứ giác OMNP có đường 0,25
kính là OP. Nên đường tròn ngoại tiếp tam giác OMN có đường kính là OP
Ta có: CN // OP và MP // CD nên tứ giác OCMP là hình bình hành và suy ra 0,25 OP = CM 3 Ta có 1 1 2
AM = AO = R  OM = R. Áp dụng định lý Pytago trong tam giác 3 3 3 0,25
vuông OMC nên tính được MC = R 13  OP = R 13 3 3
Vậy bán kính đường tròn ngoại tiếp tam giác OMN bằng R 13 0,25 6 Trang 2
Câu IV(1,0 điểm) Phần, Nội dung Điểm ý a, , b c  1 2 2 2 3 3 3
a + b + c = a + b + c = 1  2 3 2 3 2 3
a − a + b − b + c − c = 0 0,25 1
 − a  0,1− b  0, 1− c  0 1   2 2 2
a (1− a) + b (1− b) + c (1− c) = 0 Mà 2 2 2
a (1− a) + b (1− b) + c (1− c)  0  a = 1, b = c = 0 và các hoán vị của nó. 0,25 Suy ra S = 1 2 2 2
x + y + z = 6
x + y + z =12    0,25
xy + yz + zx =12
xy + yz + zx =12 2 2 2 2
(x − y) + (y − z) + (z − x) = 0  
 x = y = z = 2
x + y + z = 6 0,25 Vậy z = 2
* Chú ý: Mọi cách giải khác đúng đều được xem xét và cho điểm tối đa.
-------- Hết -------- Trang 3