Đề Thi Tuyển Sinh 10 Toán Chung Sở GD Hà Nam 2025-2026 Có Lời Giải

UBND TỈNH HÀ NAM
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
SỞ GIÁO DỤC VÀ ĐÀO TẠO
Môn: Toán (Đề chung)
Thời gian làm bài: 120 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC
(Đề thi gồm 01 trang)
Câu I. (2,0 điểm)
1. Rút gọn biểu thức A = 2 3 − 3 27 + 7 7 + 4 3. 1 1 x
2. Cho biểu thức P = − +
(với x  0, x  4 ).
2 x − 4 2 x + 4 x − 4
a) Rút gọn biểu thức P.
b) Tìm tất cả các số nguyên x để P đạt giá trị nguyên.
Câu II. (1,5 điểm) 1. Giải phương trình 2
x + 2x −15 = 0. x
 (4 − 2y) = 7 + y − 2xy
2. Giải hệ phương trình   x − =  ( y − ) . 2 14 2 3
Câu III. (1,5 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình 2 y = x ,
đường thẳng (d ) có phương trình 2
y = 2x + m − 4m + 9 (với m là tham số) và đường thẳng
() có phương trình y = (a −3)x + 4 (với a là tham số).
1. Tìm a để đường thẳng (d ) và đường thẳng () vuông góc với nhau.
2. Chứng minh đường thẳng (d ) luôn cắt parabol (P) tại hai điểm phân biệt , A B với
mọi m. Gọi A( x ; y , B x ; y (với x  x ), tìm tất cả các giá trị của tham số m sao cho 1 1 ) ( 2 2) 1 2
x − 2023 − x + 2023 = y + y − 48. 1 2 1 2
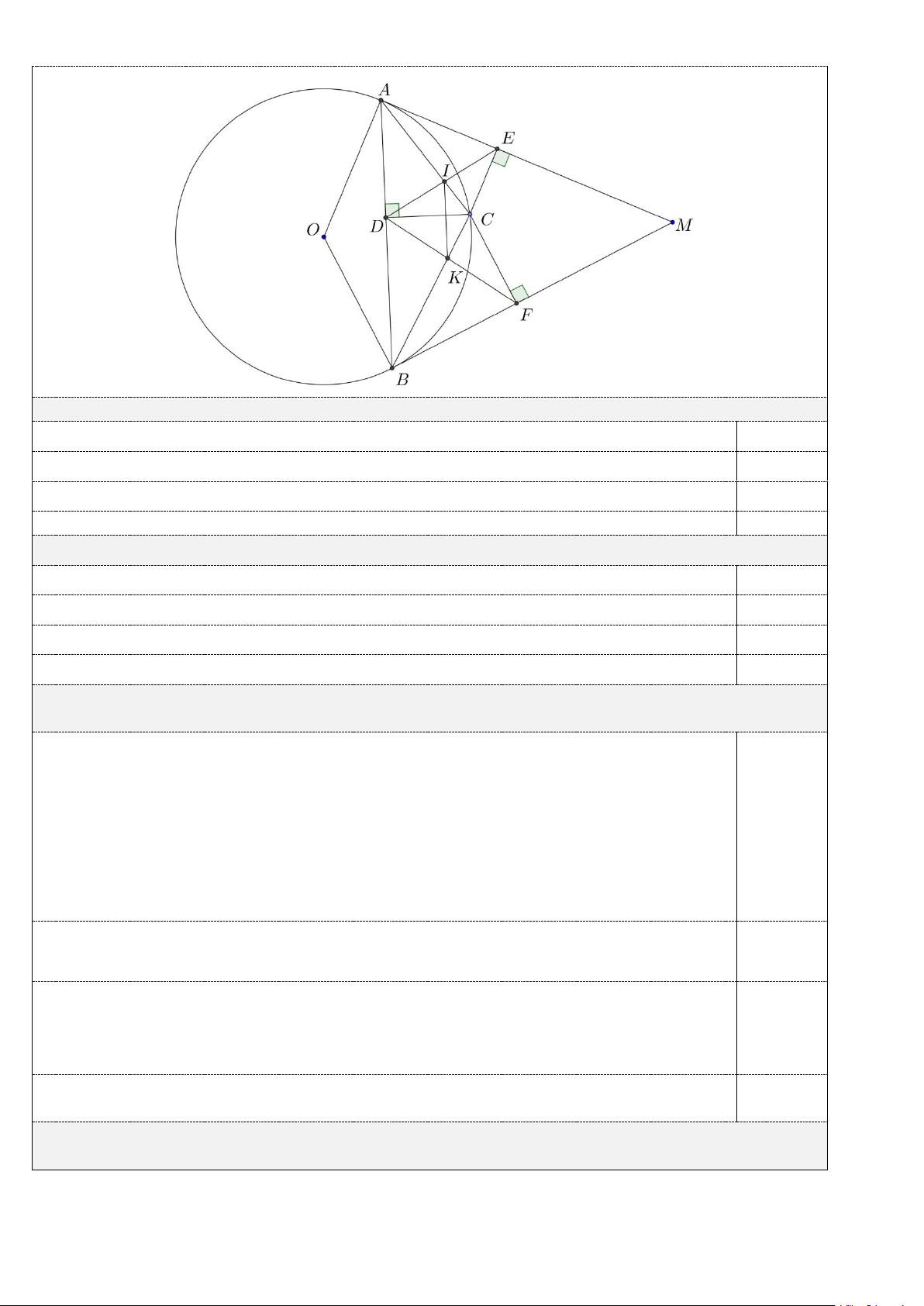
Câu IV. (4,0 điểm) Cho đường tròn (O) . Từ điểm M bên ngoài đường tròn kẻ hai tiếp tuyến M ,
A MB với đường tròn (O) ( ,
A B là các tiếp điểm). Lấy điểm C trên cung nhỏ AB
( C không nằm chính giữa cung AB , C khác A và B ). Gọi D, E, F lần lượt là hình chiếu
vuông góc của C trên các đường thẳng AB, AM , BM .
1. Chứng minh tứ giác AECD nội tiếp đường tròn.
2. Chứng minh rằng CDE = C . FD
3. Gọi I là giao điểm của AC và ED , K là giao điểm của CB và DF . Chứng minh CD ⊥ IK.
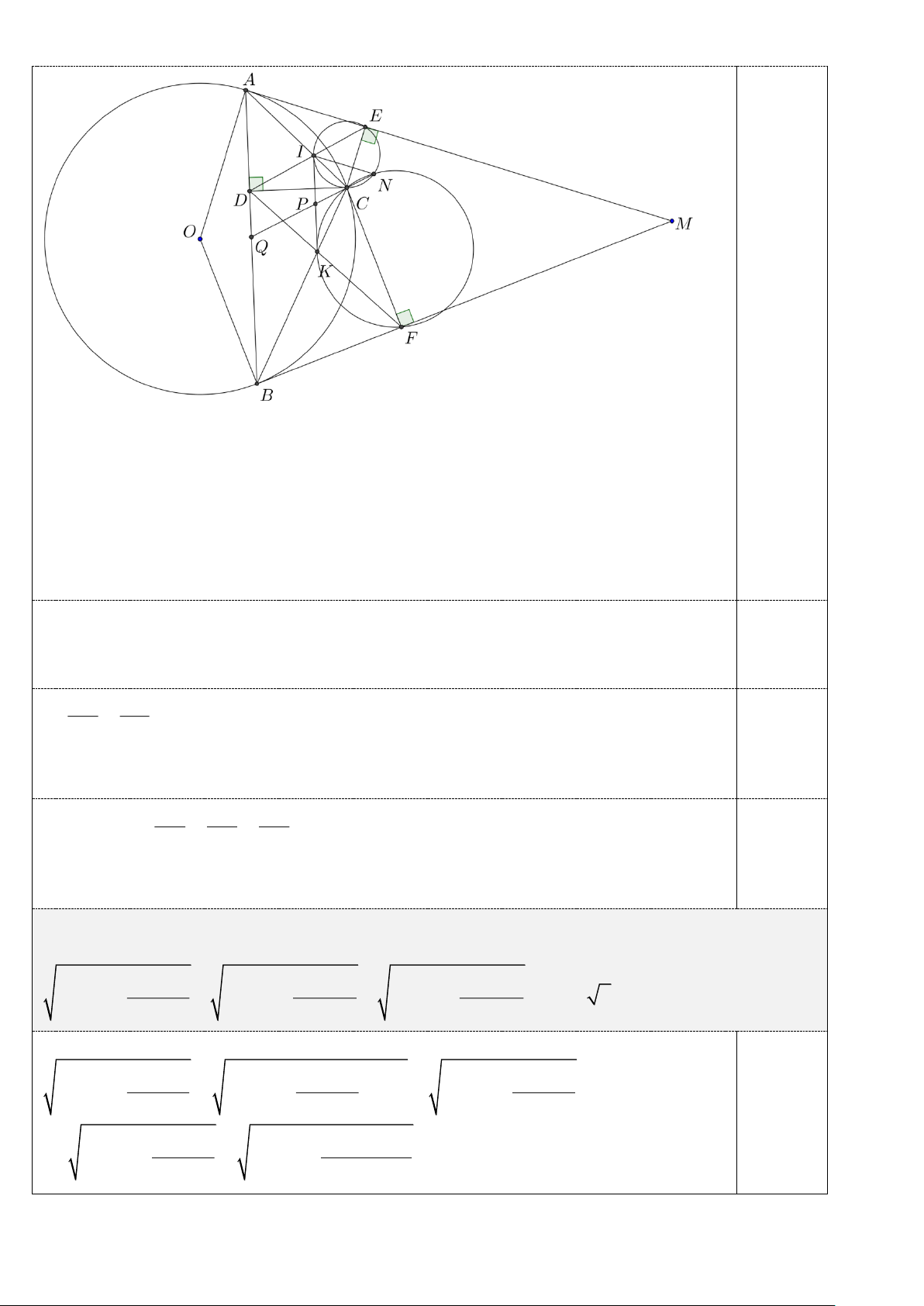
4. Đường tròn ngoại tiếp hai tam giác CIE và CKF cắt nhau tại điểm thứ hai N ( N
khác C ). Chứng minh đường thẳng NC đi qua trung điểm của đoạn thẳng AB .
Câu V. (1,0 điểm) Cho a,b,c là các số không âm thỏa mãn a + b + c = 1011. Chứng minh: (b − c)2 (c − a)2 (a −b)2 2022a + + 2022b + + 2022c +  2022 2. 2 2 2 --- HẾT---
Thí sinh được sử dụng máy tính bỏ túi không có chức năng soạn thảo văn bản và
không có thẻ nhớ.
Họ và tên thí sinh:…………………………………...Số báo danh:...................................
Cán bộ coi thi số 1…………………………......Cán bộ coi thi số 2……………................ Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN HÀ NAM
(Hướng dẫn chấm thi có 04 trang) ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN (ĐỀ CHUNG) Ghi chú:
- Điểm toàn bài không làm tròn.
- Các cách giải khác mà đúng cho điểm tương đương. Nội dung Điểm
Câu I (2,0 điểm) .
1. (1,0 điểm) Rút gọn biểu thức A = 2 3 − 3 27 + 7 7 + 4 3. A = − + ( + )2 2 3 9 3 7 2 3 0,5
A = 2 3 − 9 3 + 7(2 + 3) 0,25 A = 14 0,25 1 1 x
2. (1,0 điểm) Cho biểu thức P = − +
(với x  0, x  4 ).
2 x − 4 2 x + 4 x − 4
a) (0,5 điểm) Rút gọn biểu thức P. 8 x P = + 0,25 4x −16 x − 4 x + 2 1 P = = 0,25 x − 4 x − 2
b) (0,5 điểm) Tìm tất cả các số nguyên x để P đạt giá trị nguyên.
P đạt giá trị nguyên  x − 2 = 1  0,25
x − 2 = 1  x = 3  x = 9 (thỏa mãn điều kiện x  0, x  4 ). 0,25 x − 2 = 1
−  x = 1  x = 1(thỏa mãn điều kiện x  0, x  4 ).
Câu II (1,5 điểm).
1. (0,75 điểm) Giải phương trình 2
x + 2x −15 = 0.  ' = 1+15 = 16  0 0,25
Phương trình có hai nghiệm phân biệt 0,25 x = 1 − + 16 = 3 1 x = 1 − − 16 = 5 − 0,25 2 x
 (4 − 2y) = 7 + y − 2xy
2. (0,75 điểm) Giải hệ phương trình   x − =  ( y − ) . 2 14 2 3 x
 (4 − 2y) = 7 + y − 2xy 4x − y = 7 4x − y = 7      0,25 2x −14 = 2  ( y −3) 2x − 2y = 8 x − y = 4 3  x = 3
 x− y = 4 0,25 Trang 2 x =1   0,25 y = 3 −
Vậy hệ phương trình có nghiệm ( ; x y) = (1; 3 − )
Câu III. (1,5 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình 2 y = x ,
đường thẳng (d ) có phương trình 2
y = 2x + m − 4m + 9 (với m là tham số) và đường thẳng ()
có phương trình y = (a − 3) x + 4 (với a là tham số).
1. (0,5 điểm) Tìm a để đường thẳng (d ) và đường thẳng () vuông góc với nhau.
(d) ⊥ ()  2.(a − 3) = 1 − 0,25 5  a = . 0,25 2
2. (1,0 điểm) Chứng minh đường thẳng (d ) luôn cắt (P) tại hai điểm phân biệt với mọi . Gọi (với
), tìm tất cả các giá trị của tham số sao cho
x − 2023 − x + 2023 = y + y − 48. 1 2 1 2
Phương trình hoành độ giao điểm của đường thẳng (d ) và (P) 0,25 2 2 2 2
x = 2x + m − 4m + 9  x − 2x − m + 4m − 9 = 0( ) 1  = m − m + = (m − )2 2 ' 4 10 2 + 6  0 m  0,25
Vậy đường thẳng (d ) luôn cắt (P) tại hai điểm phân biệt ,
A B với mọi m
a c = −m + m − = −(m − )2 2 . 4 9 2 − 5  0 m   Phương trình ( ) 1 luôn có hai nghiệm
trái dấu x  0  x 1 2 0,25 x − 2023  0 1 
 x − 2023 − x + 2023 = − x + x 1 2 ( 1 2) x + 2023  0  2
x − 2023 − x + 2023 = y + y − 48  −( x + x ) 2 2 = x + x − 48 1 2 1 2 1 2 1 2
 −(x + x ) = (x + x )2 2
− 2x .x − 48  −2 = 2 − 2( 2
−m + 4m − 9 − 48 1 2 1 2 1 2 ) 0,25 m = 6 2
 m − 4m −12 = 0  .  m = 2 −
Câu IV. (4,0 điểm) Cho đường tròn (O) . Từ điểm M bên ngoài đường tròn kẻ hai tiếp tuyến M ,
A MB với đường tròn (O) ( ,
A B là các tiếp điểm). Lấy điểm C bất kì trên cung nhỏ AB (C
khác A và B ). Gọi D, E, F lần lượt là hình chiếu vuông góc của C trên các AB, AM , BM . Trang 3
1. (1,0 điểm) Chứng minh tứ giác AECD nội tiếp đường tròn.
DC ⊥ AD  ADC = 90 0,25
AE ⊥ EC  AEC = 90 0,25
ADC + AEC = 180 0,25
 Tứ giác AECD nội tiếp đường tròn. 0,25
2.(1,0 điểm) Chứng minh rằng CDE = C . FD
Tứ giác AECD nội tiếp  CDE = CAE. 0,25
CDB + CFB = 180  Tứ giác CDBF nội tiếp  CFD = CB . D 0,25
Mà CBD = CAE ( Cùng chắn cung AC ) 0,25  CDE = CF . D 0,25
3.(1,0 điểm) Gọi I là giao điểm của AC và ED , K là giao điểm của CB và DF . Chứng minh CD ⊥ IK.
Tứ giác CDBF nội tiếp  CFD = CB . D
CDE = CFD (Chứng minh trên)
 CDE = CBD hay CDI = CBA( ) 1 0,25
Tứ giác CDBF nội tiếp CDF = CBF
Mà CBF = CAB (Cùng chắn cung BC )
 CDK = CAB (2) Từ ( )
1 ,(2)  ICK + IDK = ICK + IDC + CDK = 0
ACB + CBA + CAB = 180 0,25
 Tứ giác CIDK nội tiếp
Suy ra CIK = CDK
Mà CDK = CAB (Chứng minh trên) 0,25  CIK = CAB  IK // AB 0,25
Mà CD ⊥ AB  CD ⊥ IK.
4. (1,0 điểm) Đường tròn ngoại tiếp hai tam giác CIE và CKF cắt nhau tại điểm thứ hai là N .
Chứng minh đường thẳng NC đi qua trung điểm của đoạn thẳng AB . Trang 4
Gọi NC cắt IK, AB lần lượt tại P,Q
CIK = CAB (Chứng minh trên).
Tứ giác AECD nội tiếp đường tròn  CAD = CED hay CAB = CEI  CEI = CIK
 IK là tiếp tuyến của đường tròn ngoại tiếp tam giác CIE
Chứng minh tương tự: IK là tiếp tuyến của đường tròn ngoại tiếp tam giác CKF 0,25
Xét hai tam giác PIC, PNI có
IPN chung, PIC = PNI (cùng chắn cung IC ) 0,25  P  IC∽ P  NI PI PC 2  =
 PI = PC.PN PN PI 0,25 Chứng minh tương tự: 2
PK = PC.PN Vậy PI = PK IP CP PK IK // AB  = = AQ CQ QB 0,25
Mà PI = PK  AQ = QB
Hay Q là trung điểm của AB
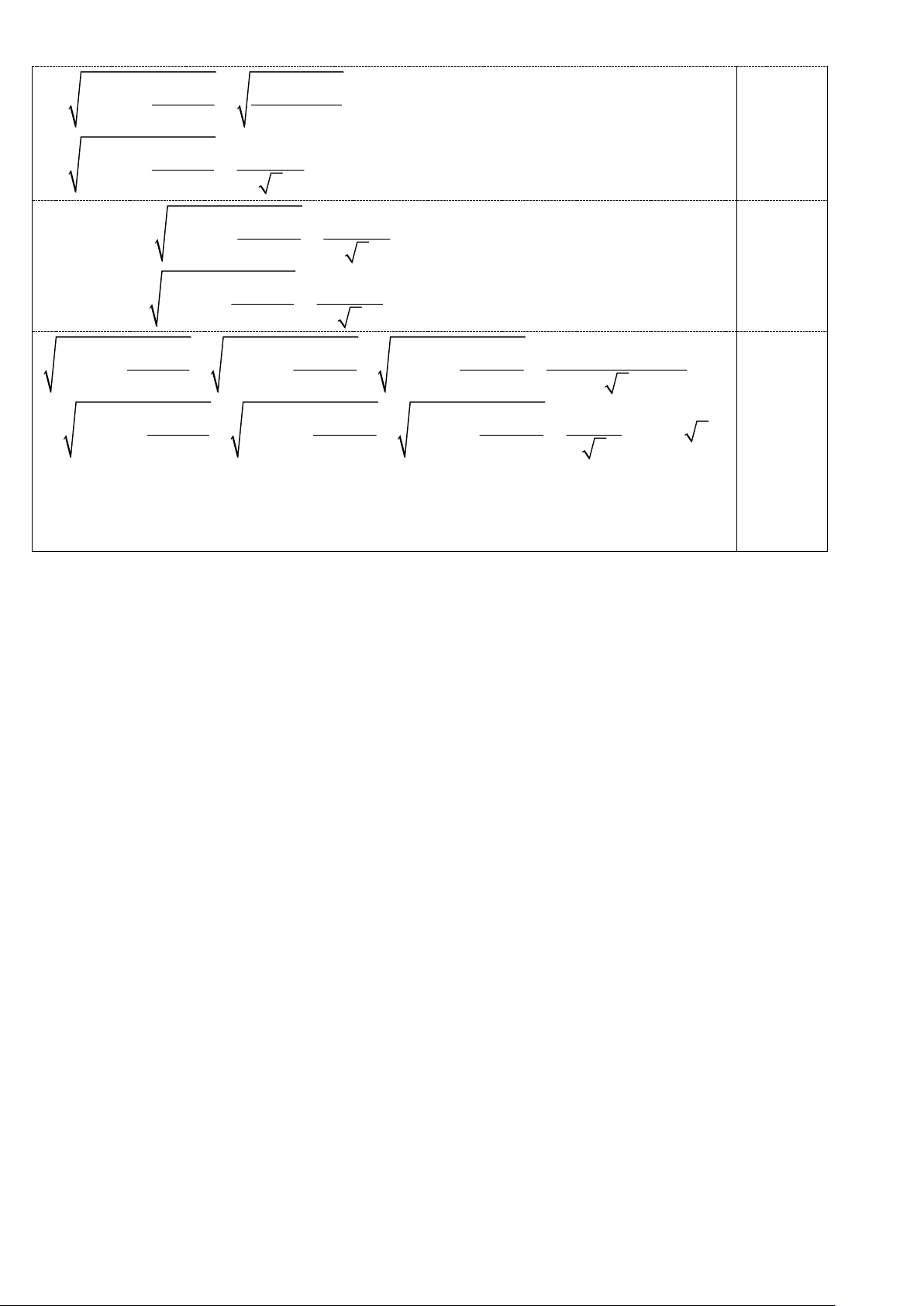
Câu V. (1,0 điểm) Cho a,b,c là các số không âm thỏa mãn a + b + c = 1011 . Chứng minh rằng: (b − c)2 (c − a)2 (a −b)2 2022a + + 2022b + + 2022c +  2022 2 2 2 2 Ta có: (b − c)2 (b + c)2 (b + c)2 2022a + = 2022a +
− 2bc  2022a + (vì bc ≥ 0) 2 2 2 0,25 (b − c)2 ( − a)2 1011  2022a +  2022a + 2 2 Trang 5 (b − c)2 ( + a)2 1011  2022a +  2 2 0,25 (b − c)2 + bc  = 0  1011 a 2022a +  dấu = xảy ra   2 2
a + b + c =1011
(c − a)2 1011+ b Tương tự: 2022b +  2 2 0,25
(c −b)2 1011+ c 2022c +  2 2 (b − c)2 (c − a)2
(a −b)2 3.1011+ a + b + c 2022a + + 2022b + + 2022c +  2 2 2 2 (b − c)2 (c − a)2 (a −b)2  4.1011 2022a + + 2022b + + 2022c +  = 2022 2 2 2 2 2 0,25
a + b + c =1011 Dấu = xảy ra  
ab = bc = ca = 0
(Khi trong ba số a,b,c có một số bằng 1011 và hai số bằng 0).
-----------------Hết----------------- Trang 6