Đề Thi Tuyển Sinh 10 Toán Chung Sở GD Quảng Bình 2025-2026 Có Lời Giải

SỞ GD&ĐT QUẢNG BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT Môn: TOÁN (CHUNG) ĐỀ CHÍNH THỨC
SBD:………….. Thời gian làm bài: 90 phút (không kể thời gian giao đề)
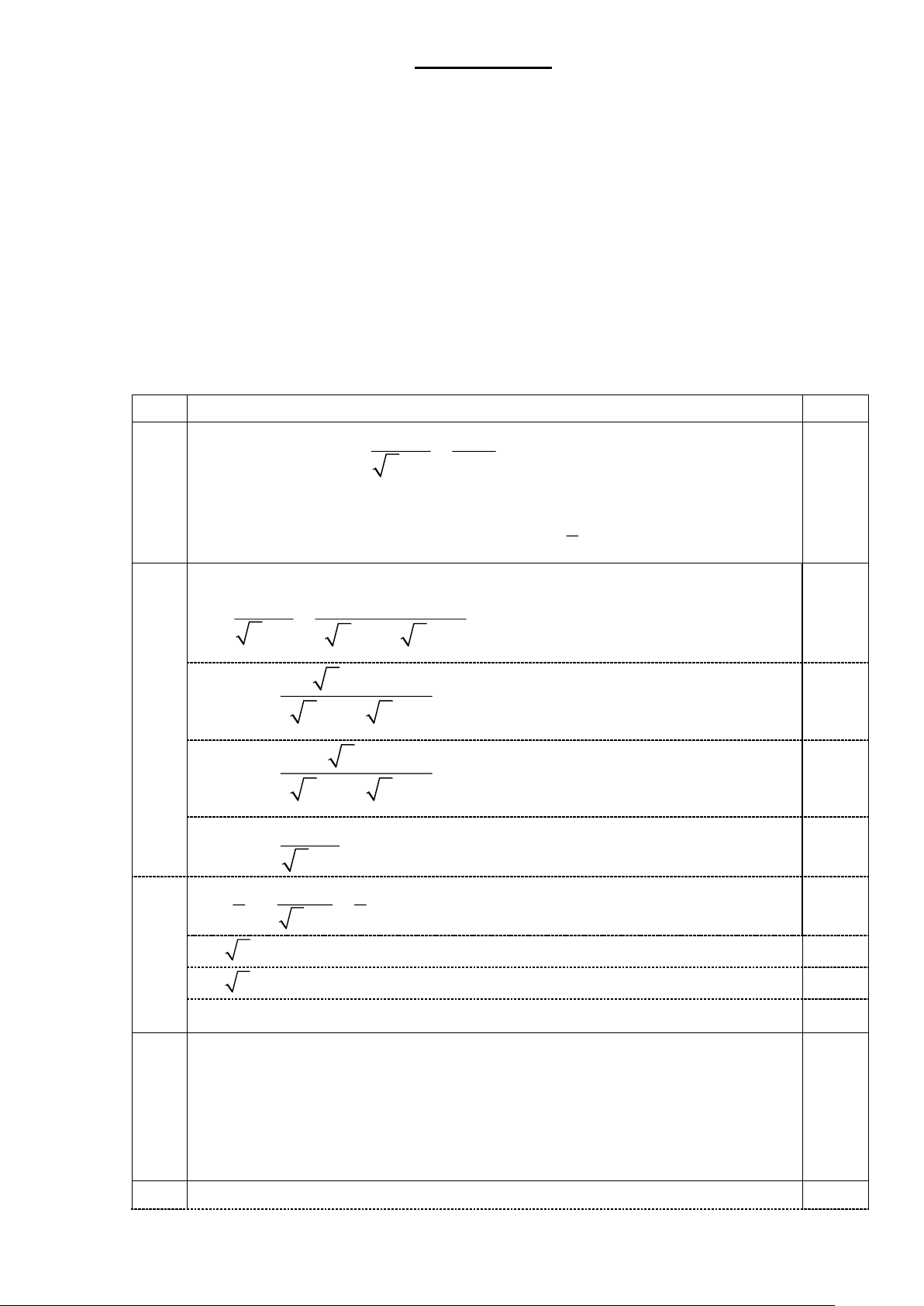
Đề có 01 trang gồm 4 câu MÃ ĐỀ: 001 Câu I (2,5 điểm) 1 4 Cho biểu thức A = +
với a  0 và a  4 . a + 2 a − 4
1. Rút gọn biểu thức A.
2. Tìm tất cả các giá trị của a để 1 A = . 2 Câu II (3,0 điểm)
1. Giải phương trình 2
x + 3x − 4 = 0 .
2. Cho phương trình 2
x + 3x + m − 3 = 0, (m là tham số).
a. Tìm tất cả các giá trị của m để phương trình có hai nghiệm.
b. Trong trường hợp phương trình có hai nghiệm x , x , tìm tất cả các giá 1 2
trị của m để x , x thỏa mãn hệ thức 2x x − x + x = 2 . 1 2 ( 1 2) 1 2 Câu III (1,0 điểm)
Với x  , tìm giá trị nhỏ nhất của biểu thức 2
P = 9x − 2 3x − 2 −12x + 2028. Câu IV (3,5 điểm)
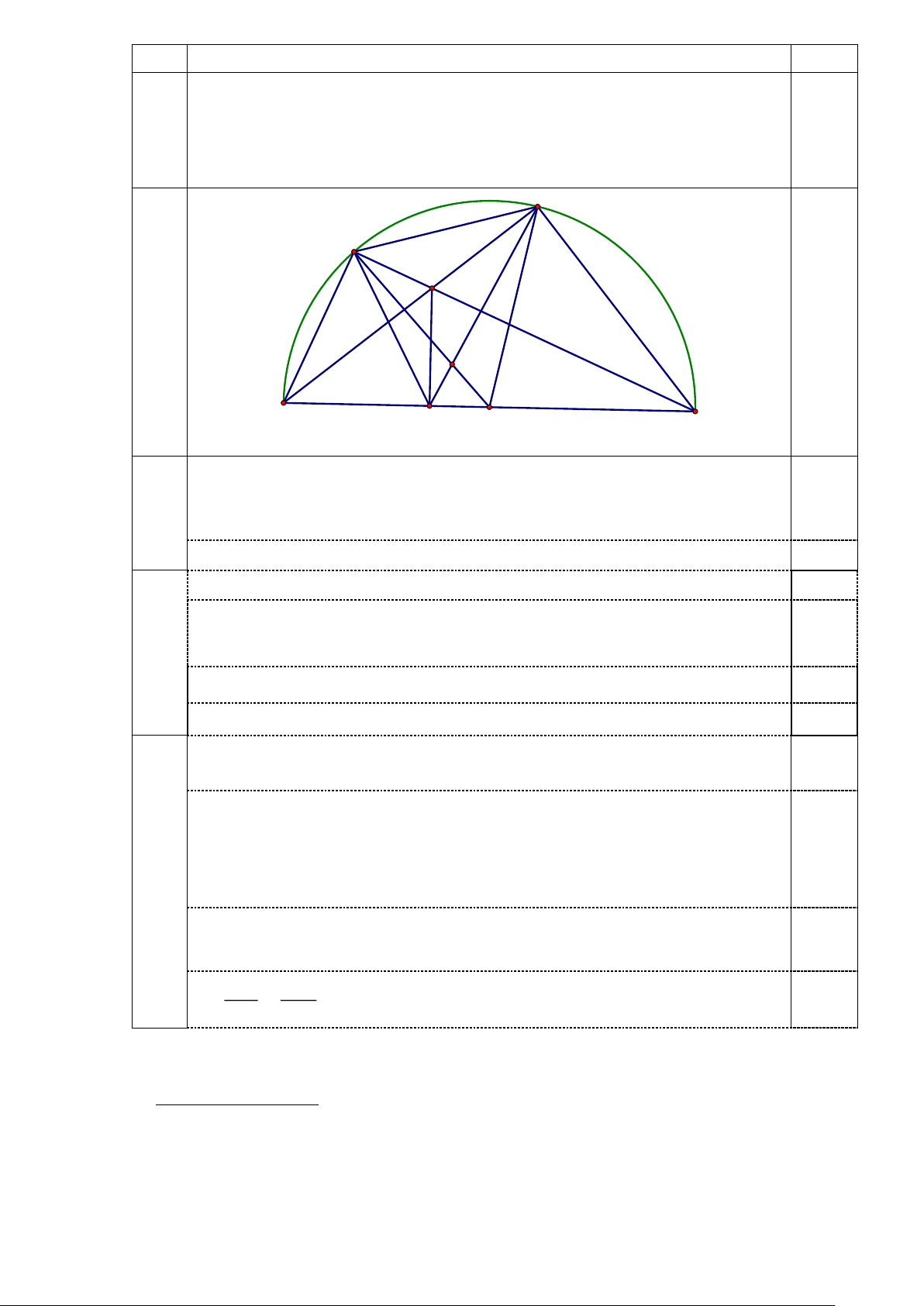
Cho nửa đường tròn tâm O đường kính AB và điểm C thuộc nửa đường
tròn đó (C khác A và B). Lấy điểm E thuộc cung AC (E khác A và C) sao cho
AE, gọi M là giao điểm của AC và BE. Kẻ MH vuông góc với AB tại H.
1. Chứng minh tứ giác BCMH nội tiếp.
2. Chứng minh ACE đồng dạng với H  CM.
3. Gọi K là giao điểm của OE và HC. Chứng minh KE.KO = KC.KH.
............................HẾT......................... Trang 0
SỞ GD&ĐT QUẢNG BÌNH HƯỚNG DẪN CHẤM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT Môn: TOÁN (CHUNG)
(Hướng dẫn chấm gồm có 03 trang) MÃ ĐỀ 001 và 003 Yêu cầu chung
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu
cầu phải lập luận logic chặt chẽ, đầy đủ, chi tiết rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với
những bước sau có liên quan.
* Điểm thành phần của mỗi câu được phân chia đến 0,25 điểm. Đối với điểm là
0,5 điểm thì tùy tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Đối với Câu 4, học sinh không vẽ hình thì cho điểm 0. Trường hợp học sinh có
vẽ hình, nếu vẽ sai ở ý nào thì điểm 0 ở ý đó.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tùy theo mức điểm từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm 1 4
Cho biểu thức A = +
với a  0 và a  4 . a + 2 a − 4 I
1. Rút gọn biểu thức A. 2,5
2. Tìm tất cả các giá trị của a để 1 A = . 2
Với a  0 và a  4 ta có 1 4 A = + 0,5
a + 2 ( a − 2)( a + 2) − + 1 a 2 4 = 0,5 ( a −2)( a +2) a + 2 = ( 0,25 a − 2)( a + 2) 1 = 0,25 a − 2 1 1 1 A =  = 0,25 2 a − 2 2 2  a − 2 = 2 0,25  a = 4 0,25 Trang 1 Câu Nội dung Điểm
 a = 16 (TM ). Vậy a = 16. 0,25
1. Giải phương trình 2
x + 3x − 4 = 0 .
2. Cho phương trình 2
x + 3x + m − 3 = 0, (m là tham số).
a. Tìm tất cả các giá trị của m để phương trình có hai nghiệm.
II b. Trong trường hợp phương trình có hai nghiệm x ,x , tìm tất 3,0 1 2
cả các giá trị của m để x , x thỏa mãn hệ thức 1 2
2x x − x + x = 2 . 1 2 ( 1 2)
Ta thấy a + b + c = 1+ 3 − 4 = 0 0,5 1
nên phương trình có hai nghiệm x = 1 và x = −4 . 1 2 0,5
Phương trình có hai nghiệm khi và chỉ khi   0 0,25
 9 − 4(m − 3)  0 0,25
2a  21− 4m  0 0,25 21  m  . Vậy 21 m  . 0,25 4 4 Khi 21 m 
thì phương trình có hai nghiệm x , x 4 1 2 x + x = 3 − 0,25 Theo Vi-ét ta có 1 2  2b x x = m − 3  1 2
Ta có 2x x − x + x = 2  2(m − 3) + 3 = 2 1 2 ( 1 2) 0,25 5
 m = (TM ) . Vậy 5 m = . 0,5 2 2
Với x  , tìm giá trị nhỏ nhất của biểu thức III 1,0 2
P = 9x − 2 3x − 2 −12x + 2028.
Ta có P = ( x)2 2 3
− 2.2.3x + 2 − 2 3x − 2 + 2024 0,25 = ( x − )2 3
2 − 2 3x − 2 +1+ 2023 = ( x − − )2 3 2 1 + 2023  2023, x   0,25
Dấu bằng xảy ra khi và chỉ khi
3x − 2 −1 = 0  3x − 2 = 1 x = 1 0,25 3x − 2 = 1     1 3x − 2 = 1 − x =  3
Vậy giá trị nhỏ nhất của P là 2023 đạt được khi x = 1 hoặc 1 x = . 0,25 3
Cho nửa đường tròn tâm O đường kính AB và điểm C
thuộc nửa đường tròn đó (C khác A và B). Lấy điểm E thuộc 3,5
IV cung AC (E khác A và C) sao cho AE, gọi M là giao điểm điểm
của AC và BE. Kẻ MH vuông góc với AB tại H. Trang 2 Câu Nội dung Điểm
1. Chứng minh tứ giác BCMH nội tiếp.
2. Chứng minh ACE đồng dạng với HCM .
3. Gọi K là giao điểm của OE và HC. Chứng minh
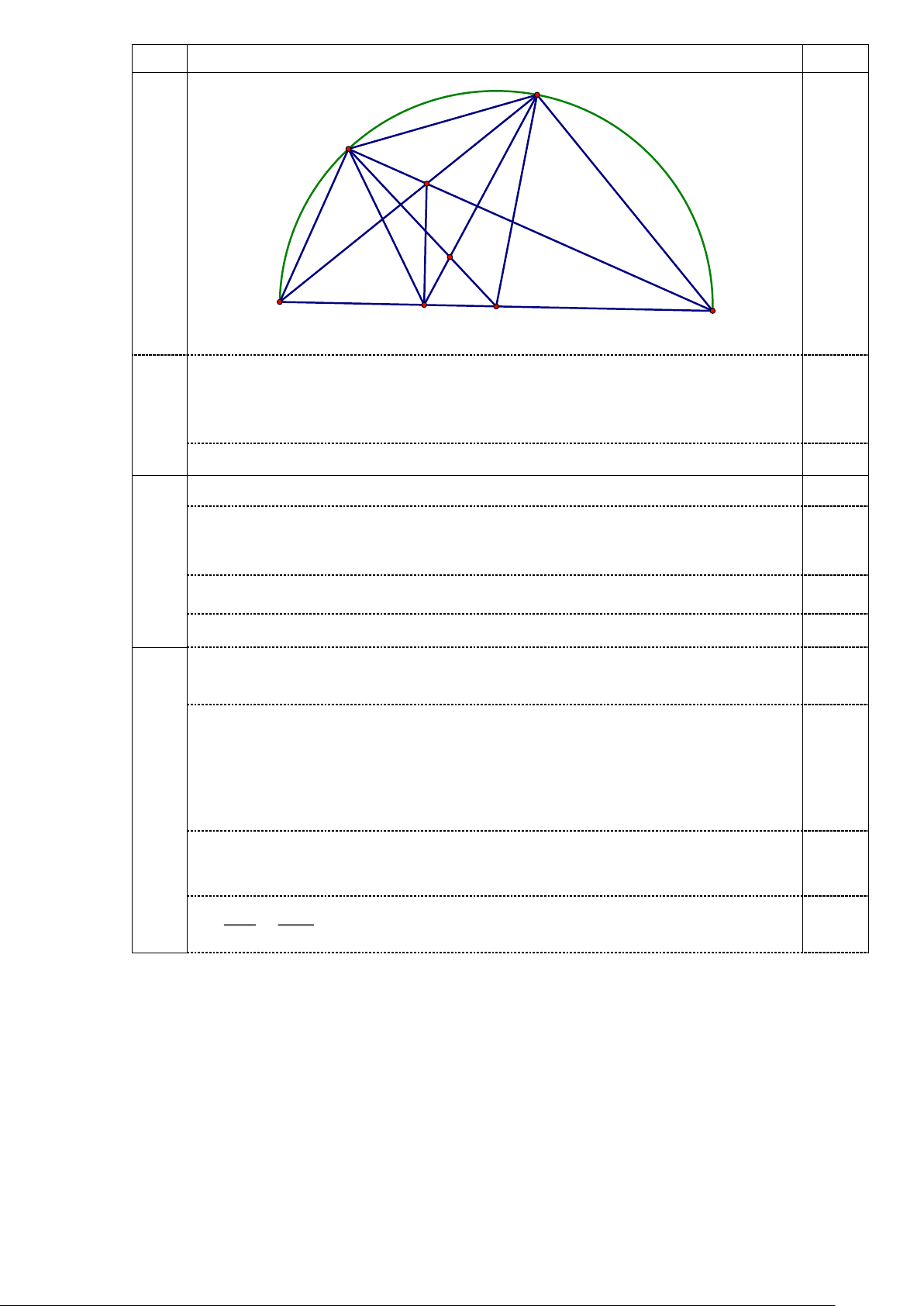
KE.KO = KC.KH. C E M 0,5 K A H O B
Học sinh vẽ hình đúng để giải Câu a cho 0,5 điểm.
Xét tứ giác BCMH có 0
BCM = ACB = 90 (góc nội tiếp chắn nửa đường tròn) 0,5 1 0
MHB = 90 (vì MH ⊥ AB ) Suy ra 0
BCM + MHB = 180 nên tứ giác BCMH nội tiếp đường tròn. 0,5
Xét ACE và HCM có: EAC = EBC (Cùng chắn cung EC ) 0,25
MHC = EBC (Cùng chắn cung MC ) 0,25 2
Suy ra EAC = MHC ( ) 1
Tương tự ta có ACE = MCH (2), (cùng bằng ABE ) 0,25 Từ ( )
1 và (2) suy ra ACE ∽ H
 CM (g − g) (đpcm) 0,25
Chứng minh được tứ giác AEMH nội tiếp 0,25
Suy ra CAB = MEH (Cùng chắn cung HM )
Mà CAB = CEB (Cùng chắn cung BC )
Suy ra CAB = MEH = CEB 0,25
Ta có COB = 2.CAB (góc nội tiếp và góc ở tâm cùng chắn BC ) 3
Do đó COB = 2.CEB = CEH nên tứ giác CEHO nội tiếp
Suy ra HEO = HCO và EHC = EOC 0,25
Nên EKH ∽ CK 
O ( g − g ) KE KH  =
 KE.KO = KC.KH 0,25 KC KO
------------------ Hết ------------
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Khóa ngày 07/6/2023 Môn: TOÁN (CHUNG)
SBD:………….. Thời gian làm bài: 90 phút (không kể thời gian giao đề) Trang 3
Đề có 01 trang gồm 4 câu MÃ ĐỀ: 002 Câu I (2,5 điểm) 1 6 Cho biểu thức A = +
với a  0 và a  9. a + 3 a − 9
1. Rút gọn biểu thức A.
2. Tìm tất cả các giá trị của a để 1 A = . 2 Câu II (3,0 điểm)
1. Giải phương trình 2
x + 5x − 6 = 0 .
2. Cho phương trình 2
x + 5x + m − 3 = 0 (m là tham số).
a. Tìm tất cả các giá trị của m để phương trình có hai nghiệm.
b. Trong trường hợp phương trình có hai nghiệm x , x , tìm tất cả các giá 1 2
trị của m để x , x thỏa mãn hệ thức 2x x − x + x = 2 . 1 2 ( 1 2) 1 2 Câu III (1,0 điểm)
Với x  , tìm giá trị nhỏ nhất của biểu thức 2
P = 4x − 2 2x − 3 −12x + 2033. Câu IV (3,5 điểm)
Cho nửa đường tròn tâm O đường kính BC và điểm A thuộc nửa đường tròn
đó, (A khác B và C). Lấy điểm E thuộc cung AB (E khác A và B) sao cho
BE, gọi M là giao điểm của AB và CE. Kẻ MH vuông góc với BC tại H.
1. Chứng minh tứ giác ACHM nội tiếp.
2. Chứng minh BAE đồng dạng với HAM .
3. Gọi K là giao điểm của OE và HA. Chứng minh KE.KO = K . A KH.
...........................HẾT.........................
SỞ GD&ĐT QUẢNG BÌNH HƯỚNG DẪN CHẤM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2023 -2024 Khóa ngày 07/6/2023 Môn: TOÁN (CHUNG)
(Hướng dẫn chấm gồm có 03 trang) MÃ ĐỀ 002 và 004 Trang 4 Yêu cầu chung
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu
cầu phải lập luận logic chặt chẽ, đầy đủ, chi tiết rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với
những bước sau có liên quan.
* Điểm thành phần của mỗi câu được phân chia đến 0,25 điểm. Đối với điểm là
0,5 điểm thì tùy tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Đối với Câu 4, học sinh không vẽ hình thì cho điểm 0. Trường hợp học sinh có
vẽ hình, nếu vẽ sai ở ý nào thì điểm 0 ở ý đó.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tùy theo mức điểm từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm 1 6
Cho biểu thức A = +
với a  0 và a  9. a + 3 a − 9 I
1. Rút gọn biểu thức A. 2,5
2. Tìm tất cả các giá trị của a để 1 A = . 2
Với a  0 và a  9 ta có 1 6 A = + 0,5
a + 3 ( a − 3)( a + 3) a − 3 + 6 = 1 ( 0,5 a − 3)( a + 3) a + 3 = ( 0,25 a − 3)( a + 3) 1 = 0,25 a − 3 1 1 1 A =  = 0,25 2 a − 3 2 2  a − 3 = 2 0,25  a = 5 0,25
 a = 25 (TM ) . Vậy a = 25 . 0,25
1. Giải phương trình 2
x + 5x − 6 = 0 .
2. Cho phương trình 2
x + 5x + m − 3 = 0 (m là tham số).
II a. Tìm tất cả các giá trị của m để phương trình có hai nghiệm. 3,0
b. Trong trường hợp phương trình có hai nghiệm x , x , tìm tất 1 2
cả các giá trị của m để x , x thỏa mãn hệ thức 2x x − x + x = 2 . 1 2 ( 1 2) 1 2 1
Ta thấy a + b + c = 1+ 5 − 6 = 0 0,5 Trang 5 Câu Nội dung Điểm
nên phương trình có hai nghiệm x = 1 và x = −6 . 1 2 0,5
Phương trình có hai nghiệm khi và chỉ khi   0 0,25
 25 − 4(m − 3)  0 0,25
2a  37 − 4m  0 0,25 37  m  . Vậy 37 m  . 0,25 4 4 Khi 37 m 
thì phương trình có hai nghiệm x , x 4 1 2 x + x = 5 − 0,25 Theo Vi-ét ta có 1 2  2b x x = m − 3  1 2
Ta có 2x x − x + x = 2  2(m − 3) + 5 = 2 1 2 ( 1 2) 0,25 3
 m = (TM ) . Vậy 3 m = . 0,5 2 2
Với x  , tìm giá trị nhỏ nhất của biểu thức III 1,0 2
P = 4x − 2 2x − 3 −12x + 2033.
Ta có P = ( x)2 2 2
− 2.3.2x + 3 − 2 2x − 3 + 2024 0,25 = ( x − )2 2
3 − 2 2x − 3 +1+ 2023 = ( x − − )2 2 3 1 + 2023  2023, x   0,25
Dấu bằng xảy ra khi và chỉ khi
2x − 3 −1 = 0  2x − 3 = 1 2x − 3 =1   0,25 2x − 3 = 1 − x = 2   x = 1
Vậy giá trị nhỏ nhất của P là 2023 đạt được khi x = 1 hoặc x = 2 . 0,25
Cho nửa đường tròn tâm O đường kính BC và điểm A thuộc nửa
đường tròn đó, (A khác B và C). Lấy điểm E thuộc cung AB (E
khác A và B) sao cho BE, gọi M là giao điểm của AB và CE.
Kẻ MH vuông góc với BC tại H. 3,5
IV 1. Chứng minh tứ giác ACHM nội tiếp. điểm
2. Chứng minh BAE đồng dạng với HAM .
3. Gọi K là giao điểm của OE và HA. Chứng minh
KE.KO = K . A KH . Trang 6 Câu Nội dung Điểm A E M 0,5 K B H O C
Học sinh vẽ hình đúng để giải Câu a cho 0.5 điểm.
Xét tứ giác ACHM có 0
MAC = BAC = 90 ( góc nội tiếp chắn nửa đường tròn) 0,5 1 0
MHC = 90 (vì MH ⊥ BC ) Suy ra 0
MAC + MHC =180 nên tứ giác ACHM nội tiếp đường tròn. 0,5
Xét BAE và HAM có ECA = EBA(Cùng chắn cung EA ) 0,25
MHA = ECA(Cùng chắn cung MA) 0,25 2
Suy ra EBA = MHA ( ) 1
Tương tự ta có BAE = MAH (2) (cùng bằng BCE ) 0,25 Từ ( )
1 và (2) suy ra BAE ∽ H
 AM (g − g) (đpcm) 0,25
Chứng minh được tứ giác BEMH nội tiếp 0,25
Suy ra CBA = MEH (Cùng chắn cung HM )
Mà CBA = CEA (Cùng chắn cung AC )
Suy ra CBA = MEH = CEA 0,25
Ta có COA = 2.CBA (góc nội tiếp và góc ở tâm cùng chắn 3 AC )
Do đó COA = 2.CEA = AEH nên tứ giác AEHO nội tiếp
Suy ra HEO = HAO và EHA = EOA 0,25
Nên EKH ∽ A
 KO (g − g) KE KH  =
 KE.KO = K . A KH 0,25 KA KO
------------------ Hết ------------------ Trang 7