Đề Thi Tuyển Sinh 10 Toán Chung Sở GD Quảng Ninh 2025-2026 Có Lời Giải

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TỈNH QUẢNG NINH
Môn thi: Toán (Dành cho mọi thí sinh)
Thời gian làm bài: 120 phút, không kể thời gian phát đề ĐỀ THI CHÍNH THỨC
(Đề thi này có 01 trang)
Câu 1. (2,75 điểm)
a) Thực hiện phép tính: 2 9 − 16 .
b) Xác định hệ số a để đồ thị của hàm số = 2
y ax đi qua điểm A(1;2). 2x + y = 7
c) Giải hệ phương trình  . x − 2y = 4 −  1 2  x −1
d) Rút gọn biểu thức P = + :  
với x  0, x  1, x  9.  x − 3 x + 3  x − 3
Câu 2. (1,75 điểm) Cho phương trình 2 x − 2(m+ )
1 x − 9 = 0, với m là tham số.
a) Giải phương trình khi m = 3;
b) Tìm các giá trị của m để phương trình có nghiệm x = 2 ;
c) Tìm các giá trị của m để phương trình có hai nghiệm phân biệt x , x sao cho x < x và 1 2 1 2
x − x = −6 . 1 2
Câu 3. (1,5 điểm)
Hai địa điểm A và B cách nhau 280 km. Hai ô tô cùng xuất phát từ A đến B. Biết vận tốc của
xe thứ nhất lớn hơn vận tốc của xe thứ hai 10 km/h và xe thứ nhất đến B sớm hơn xe thứ hai 30
phút. Tính vận tốc mỗi xe?
Câu 4. (3,5 điểm)
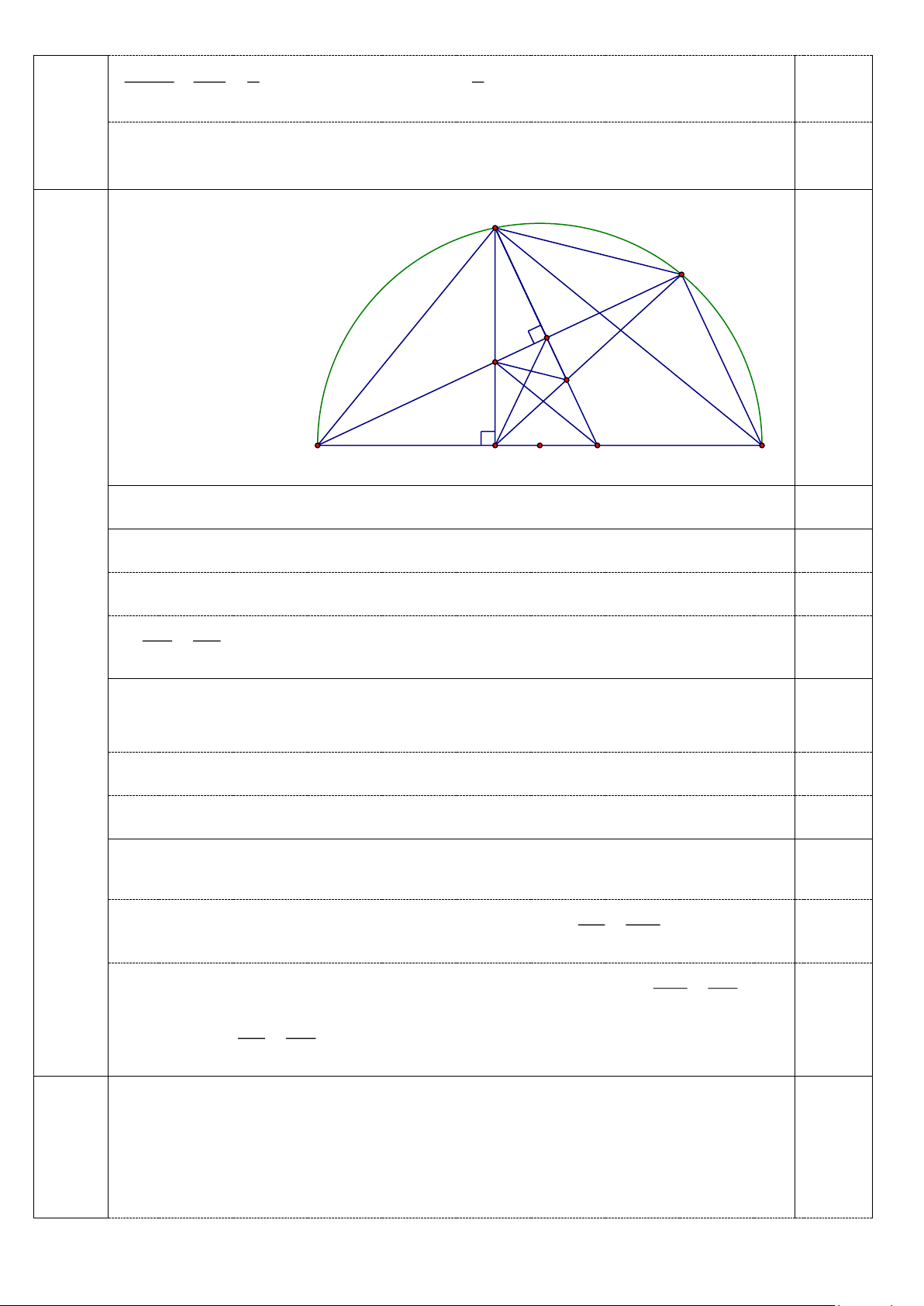
Cho nửa đường tròn tâm O, đường kính BC. Trên nửa đường tròn (O) lấy điểm A (A khác B
và C), gọi H là hình chiếu của A trên BC. Trên cung AC của nửa đường tròn (O) lấy điểm D (D
khác A và C), gọi E là hình chiếu của A trên BD, I là giao điểm của hai đường thẳng AH và BD.
a) Chứng minh tứ giác ABHE nội tiếp;
b) Chứng minh BI.BD = BH.BC;
c) Chứng minh hai tam giác AHE và ACD đồng dạng;
d) Hai đường thẳng AE và DH cắt nhau tại F. Chứng minh IF // AD.
Câu 5. (0,5 điểm)
Một người thợ cơ khí cần cắt vừa đủ một cây sắt dài 100 dm thành các đoạn để hàn lại thành
khung một hình lập phương và một hình hộp chữ nhật. Biết hình
hộp chữ nhật có chiều dài gấp 6 lần chiều rộng và chiều cao bằng
chiều rộng (hình vẽ minh họa). Tìm độ dài của các đoạn sắt sao
cho tổng thể tích của hai hình thu được nhỏ nhất?
............................ Hết ...........................
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ................................................................... Số báo danh: ..............................................
Chữ kí của cán bộ coi thi 1:..................................... Chữ kí của cán bộ coi thi 2:....................................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM THI TUYỂN SINH TỈNH QUẢNG NINH VÀO LỚP 10 THPT
Môn thi : Toán (Dành cho mọi thí sinh) ĐỀ THI CHÍNH THỨC
(Hướng dẫn này có 03 trang) Câu
Sơ lược lời giải Điểm a) 2 9 − 16 = 6 − 4 = 2 . 0,5
b) Đồ thị của hàm số = 2
y ax đi qua điểm A(1;2) 2  .1 a = 2  a = 2 . 0,5 2x + y = 7 4x + 2y =14 c)    0,25 x − 2y = 4 − x − 2y = 4 − 5  x =10 x = 2    x − 2y = 4 − y = 3 0,5 1
Vậy hệ phương trình có nghiệm ( ; x y) = (2;3) . (2,75đ)  2 −    x − x + ( x 3 1 2 1 3 ) x −1 d) P = :   + = + :   0,5  x − 3 x + 3 
x − 3  ( x −3)( x + 3) ( x −3)( x + 3)  x −3  3 x − 3 x −1 P = ( : 0,25 x − 3)( x + 3) x − 3 3( x − ) 1 x − 3 3 P = ( . = . 0,25 x − 3)( x + 3) x −1 x + 3
a) Với m = 3, ta có phương trình 2
x − 8x − 9 = 0 0,25 Do 1− ( 8 − ) + ( 9
− ) = 0 nên phương trình có hai nghiệm là: x = 1 − , x = 9 . 1 2 0,25 2 9
b) Phương trình có nghiệm x = 2 nên 2 2 − 2(m+ ) 1 2
. − 9 = 0 m = − . 0,5 4 (1,75đ) c) Ta có 1.( 9)
−  0 nên phương trình luôn có hai nghiệm phân biệt x , x 1 2 0,25
Theo định lý Vi-ét ta có x .x = 9
− và x + x = 2m+ 2 0,25 1 2 1 2
Vì x  x , x .x  0  x  0  x ; x − x = −6  −x − x = −6  m = 2 . 1 2 1 2 1 2 1 2 1 2 0,25
Gọi vận tốc của xe thứ nhất là x (km/h), x  10 . 0,25 280
Vận tốc của xe thứ hai là x −10 (km/h). Thời gian đi từ A đến B của xe thứ nhất là x 0,5 3 280
(1,5đ) (giờ). Thời gian đi từ A đến B của xe thứ hai là (giờ). x −10 280 280 1 Ta có phương trình : − = 0,25 x −10 x 2 Trang 2 280 280 1 1 −
=  280x − 280x + 2800 = x(x −1 ) 0  2
x −10x − 5600 = 0 0,25 x −10 x 2 2
Giải phương trình được x = 80 ( thỏa mãn đk), x = −70 (không thỏa mãn đk). Vậy vận 1 2 0,25
tốc của xe thứ nhất là 80 (km/h), vận tốc của xe thứ hai là 70 (km/h). Hình vẽ (đủ cho ý a) A D E 0,25 I F B H O M C a) Tứ giác ABHE có 0
AHB = AEB = 90 nên nội tiếp. 0,75
b) D thuộc nửa đường tròn đường kính BC nên 0 BDC = 90 0,25  S
BHI và  BDC có B chung, 0
BHI = BDC = 90 nên  BHI  BDC 0,5 4 BI BC (3,5đ)  =
 BI.BD = BH.BC . 0,25 BH BD
c) Tứ giác ABHE nội tiếp nên HAE = HBE mà CBD = CAD (nội tiếp (O) cùng chắn 0,25
DC )  HAE = CAD
Tứ giác ABHE nội tiếp nên AHE = ABE mà ABD = ACD  AHE = ACD 0,25  S
AHE và  ACD có HAE = CAD và AHE = ACD nên  AHE  ACD. 0,25
d) Gọi M là giao của AF và BC.  MBA có BE ⊥ AM, AH ⊥ BM nên I là trực tâm hay 0,25 IM ⊥ AB. HI HM
A thuộc (O) đường kính BC nên AB ⊥ AC  IM // AC  = (1) 0,25 HA HC HM HF
AM ⊥ BD, CD ⊥ BD (D thuộc (O) đường kính BC) nên AM // CD  = , kết HC HD 0,25 HI HF hợp với (1)  =
từ đó suy ra IF // AD. HA HD
Gọi cạnh của hình lập phương là x , các kích thước của hình hộp chữ nhật tương ứng
rộng, dài, cao là y, 6 y, y với x  0, y  0 (đơn vị dm). 5 0.25
(0,5đ) Do tổng độ dài các cạnh của hai hình là 100 dm nên tính được 3x + 8y = 25. Tổng thể tích của hai hình là 3 3
V = x + 6y (dm3). Trang 3 3
x  27x − 54 Chứng minh được 
 V  9(3x + 8y) −150 = 75 3
6y  72y − 96 x = 3
V đạt giá trị nhỏ nhất là 75 khi  . 0,25  y = 2
Vậy người thợ cần cắt cây sắt dài 100 dm thành 12 đoạn 3 dm, 8 đoạn 2 dm và 4 đoạn 12 dm.
Những chú ý khi chấm thi:
1. Hướng dẫn chấm này chỉ trình bày sơ lược một cách giải. Bài làm của học sinh phải chi
tiết, lập luận chặt chẽ, tính toán chính xác mới cho điểm tối đa.
2. Các cách giải khác nếu đúng vẫn cho điểm. Tổ chấm trao đổi và thống nhất điểm chi tiết.
3. Có thể chia nhỏ điểm thành phần nhưng không dưới 0,25 điểm và phải thống nhất trong
cả tổ chấm. Điểm thống nhất toàn bài là tổng số điểm các bài đã chấm, không làm tròn.
…………….………Hết…………….……… Trang 4