Đề Thi Tuyển Sinh 10 Toán Chuyên Sở GD Đăk Nông 2025-2026 Có Đáp Án

SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 ĐĂK NÔNG
Môn: TOÁN (chuyên)
Thời gian làm bài: 150 phút (không kể thời gian giao đề) x - 1 x - 1 1- x
Câu 1. (1,5 điểm) Với x > 0 , cho các biểu thức A = và B = + . x x x + x
a) Tính giá trị biểu thức A khi x = 64 .
b) Rút gọn biểu thức B . A 3
c) Tìm x để > . B 2 Câu 2. (2,0 điểm)
a) Giải phương trình: (x + )4 + (x + )4 3 5 = 82 .
ìï y(y - x) 2 = 2x + 3x + 1
b) Giải hệ phương trình: ïí 2
ïï x + y - x- y + 7 = 7y - 3x + 1 ïî Câu 3. (2,0 điểm) 1 1
a) Cho parabol (P) 2 : y =
x và đường thẳng (d) 2 : y = mx -
m + m + 1 với m là tham số. 2 2
Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x , x sao cho x - x = 2 . 1 2 1 2
b) Tìm tất cả các nghiệm nguyên (x, y) của phương trình: xy - x + 3y = 6 .
Câu 4. (0,5 điểm) Cho tập hợp A = {201; 203; ...; 2021; 202 }
3 gồm 912 số tự nhiên lẻ. Cần chọn ra ít
nhất bao nhiêu số từ tập hợp A sao cho trong các số được chọn luôn tồn tại hai số có tổng bằng 2288 ?
Câu 5. (3,0 điểm) Cho tam giác ABC có 3 góc nhọn (AB < AC). Vẽ đường cao AD, BE, CF của
tam giác đó. Gọi H là giao điểm của các đường cao vừa vẽ. Gọi M , N lần lượt là trung điểm
của các đoạn thẳng AH và BC .
a) Chứng minh rằng D MFN là tam giác vuông.
b) Chứng minh DFMN : DFAC .
c) Gọi P, Q lần lượt là chân các đường vuông góc từ M , N đến đường thẳng DF . Chứng
minh rằng giao điểm của FE và MN thuộc đường tròn đường kính PQ .
Câu 6. (0,5 điểm) Cho a, b là 2 số thực dương.
a) Chứng minh rằng (1+ a)(1+ b)³ 1+ ab .
b) Cho a + b = ab thỏa mãn 2
a + 3a - b ³ 0 và 2
b + 3b - a ³ 0 . 1 1
Tìm giá trị nhỏ nhất của biểu thức: P = + + ( 2 1+ a )( 2 1+ b . 2 2 )
a + 3a - b
b + 3b - a
---------------------------------@Hết@--------------------------------- Trang 1 HƯỚNG DẪN GIẢI x - 1 x - 1 1- x
Câu 1. (1,5 điểm) Với x > 0 , cho các biểu thức A = và B = + . x x x + x
a) Tính giá trị biểu thức A khi x = 64 .
b) Rút gọn biểu thức B . A 3
c) Tìm x để > . B 2 Lời giải
a) Tính giá trị biểu thức A khi x = 64 .
Ta có: x = 64 (thỏa mãn điều kiện x > 0 ). Khi đó: 64 - 1 8- 1 7 A = = = . 64 8 8 7 Vậy A = khi x = 64 . 8
b) Rút gọn biểu thức B . x - 1 1- x x - 1 x - 1 Ta có: B = + = - x x + x x x ( x + ) 1 x x x ( x - - - + )1 1 1 x - 1 = . x ( x + ) = = 1 x ( x + ) 1 x + 1 x - 1 Vậy B = với x > 0 . x + 1 A 3
c) Tìm x để > . B 2 A 3 x - 1 x - 1 3 Ta có: > Þ : > B 2 x x + 1 2 A 3 x - 1 x - 1 3 x - 1 x + 1 3 > Þ : > Þ × > B 2 x x + 1 2 x x - 1 2
(ĐKXĐ: x > 0 và x ¹ 1) x + 1 3 2 x + 2 - 3 x Þ - > 0 Û > 0 Û 2 -
x > 0 (vì x > 0 ) x 2 2 x Û
x < 2 Þ x < 4 .
Kết hợp điều kiện, ta được 0 < x < 4 và x ¹ 1. A 3 Vậy >
khi 0 < x < 4 và x ¹ 1. B 2 Câu 2. (2,0 điểm)
a) Giải phương trình: (x + )4 + (x + )4 3 5 = 82 .
ìï y(y - x) 2 = 2x + 3x + 1
b) Giải hệ phương trình: ïí 2
ïï x + y - x- y + 7 = 7y - 3x + 1 ïî Trang 2 Lời giải
a) Giải phương trình: (x + )4 + (x + )4 3 5 = 82 .
Đặt x + 4 = t . Khi đó phương trình trở thành: (t - )4 + (t + )4 1 1 = 82 4 3 2 4 3 2
Û t - 4t + 6t - 4t + 1+ t + 4t + 6t + 4t + 1= 82 4 2 Û t + t - = Û ( 2 t + )( 2 6 40 0 10 t - ) 4 = 0 2 Û t = 4 (vì 2
t + 10 > 0 " t )
ét = 2 Þ x = - 2 Û ê .
êt = - 2 Þ x = - 6 ë Vậy S = {- 2; - } 6 .
ìï y(y - x) 2
= 2x + 3x + 1 ( ) 1
b) Giải hệ phương trình: ïí 2
ïï x + y - x- y + 7 = 7y - 3x + 1 (2) ïî ìï x + y ³ 0 ĐKXĐ: ïí
ï x - y + 7 ³ 0 ïî PT (1) 2 2
Û 2x + xy - y + 3x + 1= 0 Û (x + y)(2x - y)+ (x + y)+ (2x - y)+ 1= 0 Û (x + y + ) 1 (2x - y + )
1 = 0 Û y = 2x + 1 (vì x + y ³ 0 nên x + y + 1> 0 ).
Thay vào phương trình (2), ta được: 2 x + 2x + 1 -
x - 2x - 1+ 7 = 14x + 7 - 3x + 1 2 1 Û 3x + 1 -
6 - x + 3x - 14x - 8 = 0 (ĐKXĐ: - £ x £ 5 ) 3
Û ( x + - )- ( - x - ) 2 3 1 4 6
1 + 3x - 14x - 5 = 0 3x + 1- 16 6 - x - 1 Û - + (x - ) 5 (3x + ) 1 = 0 3x + 1 + 4 6 - x + 1 æ ö Û (x - ) 3 1 5 ç ×ç + + 3x + 1÷ ÷= 0 ç çè 3x + 1 + 4 6- x + 1 ÷ ÷ø 1 3 1 Vì x ³ - nên + + 3x + 1> 0 3 3x + 1 + 4 6 - x + 1
Do đó x = 5 Þ y = 11 (thỏa mãn).
Vậy (x, y)= (5; ) 11 . Câu 3. (2,0 điểm) 1 1
a) Cho parabol (P) 2 : y =
x và đường thẳng (d) 2 : y = mx -
m + m + 1 với m là tham số. 2 2
Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x , x sao cho x - x = 2 . 1 2 1 2
b) Tìm tất cả các nghiệm nguyên (x, y) của phương trình: xy - x + 3y = 6 . Lời giải 1 1
a) Cho parabol (P) 2 : y =
x và đường thẳng (d) 2 : y = mx -
m + m + 1 với m là tham số. 2 2
Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x , x sao cho x - x = 2 . 1 2 1 2 Trang 3
Phương trình hoành độ giao điểm của (P) và (d) là: 1 1 2 2 2 2 x = mx -
m + m + 1 Û x - 2mx + m - 2m - 2 = 0 (1) 2 2
Ta có: D¢= b¢ - ac = (- m)2 2 - ( 2 1 m - 2m - ) 2 = 2m + 2
Để (P) và (d) cắt nhau tại hai điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt ìï a ¹ 0 ìï1¹ 0 ï ï Û í Þ í Û m > - 1. ï D¢> 0 ï 2m + 2 > 0 ïî ïî
Với m > - 1 có 2 nghiệm phân biệt. Áp dụng hệ thức Vi-ét, ta có: ìï - ï b x + x = = 2 ï m 1 2 ï a í . ï c 2
ïï x .x = = m - 2m- 2 1 2 ïïî a
Ta có: x - x = 2 Û (x - x )2 = 4 Û (x + x )2 - 4x x = 4 1 2 1 2 1 2 1 2 Þ (2m)2 - 4( 1 2 m - 2m - )
2 = 4 Û 2m + 2 = 1 Û m = - (tm). 2 1 Vậy m = - . 2
b) Tìm tất cả các nghiệm nguyên (x, y) của phương trình: xy - x + 3y = 6 .
Ta có: xy - x + 3y = 6 Û x(y - ) 1 + ( 3 y - ) 1 = 3 Û (x + ) 3 (y - ) 1 = 3 .
Vì x, y nguyên nên ta có các trường hợp sau: x + 3 - 3 - 1 1 3 y - 1 - 1 - 3 3 1 x - 6 - 4 - 2 0 y 0 - 2 4 2
Vậy (x, y)= (- 6; 0), (- 4; - 2), (- 2; 4), (0; 2).
Câu 4. (0,5 điểm) Cho tập hợp A = {201; 203; ...; 2021; 202 }
3 gồm 912 số tự nhiên lẻ. Cần chọn ra ít
nhất bao nhiêu số từ tập hợp A sao cho trong các số được chọn luôn tồn tại hai số có tổng bằng 2288 ? Lời giải
Xét các cặp số (a, b) trong tập hợp A có tổng bằng 2288 là: (2023; 26 ) 5 , (2021; 267), (2019; 26 ) 9 , ..., (1147;11 ) 41 , (1145;11 ) 43 (*)
Số các cặp số (a, b) trong tập hợp A có tổng bằng 2288 là: 2023- 1145 + 1= 440. 2
Số các số trong tập hợp A mà không có số ghép đôi để tổng bằng 2288 là: 912 - 2.440 = 32 .
Chọn ra 441 số từ (*), theo Dirichlet tồn tại một nhóm chứa 2 số có tổng bằng 2288.
Vậy cần chọn ít nhất 441+ 32 = 473 số từ tập hợp A luôn tồn tại hai số có tổng bằng 2288 . Trang 4
Câu 5. (3,0 điểm) Cho tam giác ABC có 3 góc nhọn (AB < AC). Vẽ đường cao AD, BE, CF của
tam giác đó. Gọi H là giao điểm của các đường cao vừa vẽ. Gọi M , N lần lượt là trung điểm
của các đoạn thẳng AH và BC .
a) Chứng minh rằng D MFN là tam giác vuông.
b) Chứng minh DFMN : DFAC .
c) Gọi P, Q lần lượt là chân các đường vuông góc từ M , N đến đường thẳng DF . Chứng
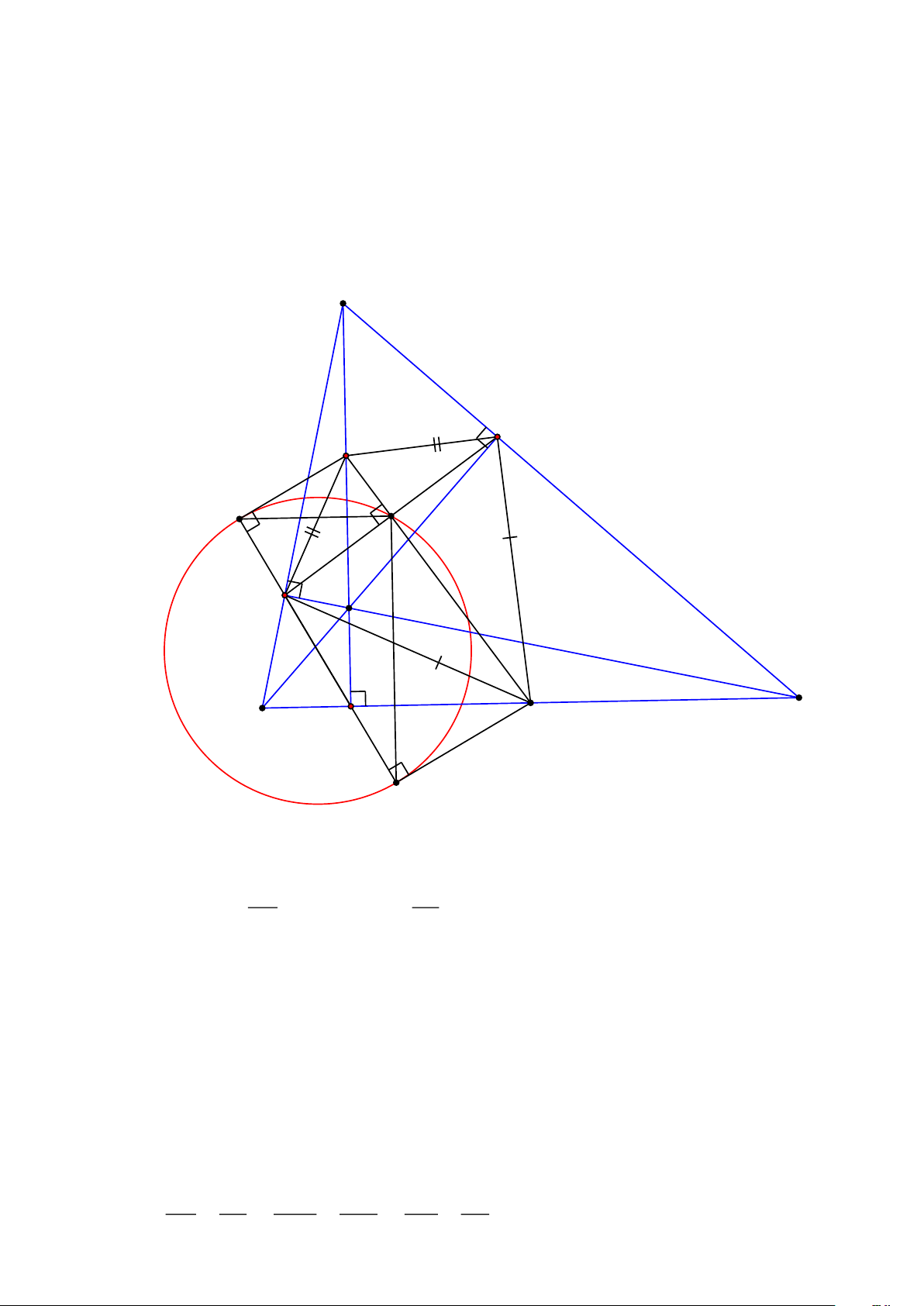
minh rằng giao điểm của FE và MN thuộc đường tròn đường kính PQ . Lời giải A M E P G H F B C D N Q
a) Chứng minh rằng D MFN là tam giác vuông.
Ta có các tam giác FHA và tam giác FBC là các tam giác vuông nên có AH BC FM = MA = và FN = NB =
( tính chất đường trung tuyến ứng với cạnh huyền ) 2 2 · ·
Þ MFA = BAD và · · NFB = DBA · · · ·
Þ MFA+ NFB = BAD + DBA = 90° ( vì tam giác BAD vuông tại D ) · · ·
Þ MFN = 180° - MFA- NFB = 180° - 90° = 90° Þ D MFN là tam giác vuông
b) Chứng minh DFMN : DFAC .
+) Xét D BFC và D HFA có: · ·
AFH = BFC = 90° · ·
FAH = FCB (cùng phụ · ABC )
Þ DBFC : DHFA(g.g) AH BC 2AM 2CN AM CN Þ = Þ = Þ = . AF FC AF FC AF FC Trang 5
+) Xét D AMF và D CNF có: AM CN = (chứng minh trên) AF FC · ·
FAH = FCB (cùng phụ · ABC )    ( FM FN AMF CNF . c g.c)  = AF FC
+) Xét D FMN và D FAC có: FM FN = (chứng minh trên) AF FC · ·
AFC = MFN (= 90 ) °
Þ DFMN : DFAC( . c g.c). æ 1 ö æ 1 ö
Cách khác: Ta có: MF = ME ç ÷ = ç
AH ÷ và NF = NE ç ÷ ç = ç BC÷ è 2 ÷ ø çè 2 ÷ ø
Þ MN là đường trung trực của FE
mà D NFE cân tại N (NF = NE)
Þ MN đồng thời là đường phân giác của D NFE · 1 · Þ FNM = FNE (3) 2
+) Ta có: tứ giác BFEC nội tiếp đường tròn tâm N (chứng minh câu a) · 1 · Þ FCE =
FNE (góc nội tiếp và góc ở tâm cùng chắn cung FE ) (4) 2 æ 1 ö Từ (3), (4) suy ra · · FNM = FCA ç · ÷ = ç
FNE÷.Þ DFMN : DFAC( . c g.c) çè 2 ÷ ø Ý c) BC
Gọi G là giao điểm của MN và FE Þ MN ^ FE tại G ( do NF = NE = và 2 AH MF = ME =
nên MN là đường trung trực của EF ) 2
+) Ta có: Tứ giác MPFG nội tiếp · ·
(MPF + MGF = 180 )° · · Þ GPF = GMF .
+) Ta có: Tứ giác GFQN nội tiếp · ·
(FGN + FQN = 180 )° · · Þ GQF = GNF Cộng lại ta được · · · ·
GPF + GQF = GMF + GNF = 90° (vì tam giác MFN vuông ở F ) ·
Þ PGQ = 90°. Vậy giao điểm của FE và MN thuộc đường tròn đường kính PQ .
Câu 6. (0,5 điểm) Cho a, b là 2 số thực dương.
a) Chứng minh rằng (1+ a)(1+ b)³ 1+ ab .
b) Cho a + b = ab thỏa mãn 2
a + 3a - b ³ 0 và 2
b + 3b - a ³ 0 . 1 1
Tìm giá trị nhỏ nhất của biểu thức: P = + + ( 2 1+ a )( 2 1+ b . 2 2 )
a + 3a - b
b + 3b - a Trang 6 Lời giải
a) Chứng minh rằng (1+ a)(1+ b)³ 1+ ab .
Ta có: (1+ a)(1+ b)³ 1+ ab Û 1+ a + b + ab ³ 1+ ab + 2 ab
Û ( a - b)2 ³ 0 . Dấu “=” xảy ra khi a = b .
b) Cho a + b = ab . Tìm giá trị nhỏ nhất của biểu thức: 1 1 P = + + ( 2 1+ a )( 2 1+ b . 2 2 )
a + 3a - b
b + 3b - a 1 1 4
Áp dụng bất đẳng thức + ³ , ta có: x y x + y 1 1 4 4 + ³ = 2 2
a + 3a - b
b + 3b - a ( 2 a + 3a - ) b + ( 2
b + 3b - a) 2 2
a + b + 2(a + b) 1 1 4 4 + ³ =
(vì a + b = ab ) 2 2 2 2
a + 3a - b
b + 3b - a
a + b + 2ab (a + b)2 Mặt khác ( 2 + a )( 2 1
1+ b )³ 1+ ab = 1+ (a + b) (theo câu a) 4 4 a + b a + b 7(a + b) Suy ra P ³ + 1+ (a + b)= + + + + 1 (a + b)2 (a + b)2 16 16 8
+) Áp dụng bất đẳng thức Cô – sy cho 3 số dạng x + y + z ³ 3 xyz , ta có: 4 a + b a + b 4
a + b a + b 3 + + ³ 33 × × = (1) (a + b)2 16 16 (a + b)2 16 16 4 (a + b)2
+) Ta có: a + b = ab £
Û (a + b)2 - 4(a + b)³ 0 4
Û (a + b)(a + b - 4)³ 0 Û a + b ³ 4 (vì a, b > 0 nên a + b > 0 ) 7(a + b) 7 Þ ³ (2) 8 2 3 7 21
Từ (1), (2) suy ra P ³ + + 1= . 4 2 4
Dấu “=” xảy ra khi a = b = 2 . 21
Vậy giá trị nhỏ nhất của P =
khi a = b = 2 . 4
---------------------------------@Hết@--------------------------------- Trang 7