Đề Thi Tuyển Sinh 10 Toán Chuyên Sở GD Nghệ An 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 NGHỆ AN
TRƯỜNG THPT CHUYÊN PHAN BỘI CHÂU Đề chính thức Môn thi: TOÁN
Thời gian: 150 phút, không kể thời gian giao đề
(Đề gồm có 01 trang)
Câu 1 (6,0 điểm). a) Giải phương trình 4 3 2
x − 4x + 6x − 4x − 3 = 0 . 2
2x − x + y = 2y − x + 2x 
b) Giải hệ phương trình ( .  2 − x + y  ) 2x +4 = 2 3x
Câu 2 (3,0 điểm).
a) Tìm x  R sao cho x + 2024 và 1 − 2024 đều là các số nguyên. x
b) Tìm số nguyên dương a nhỏ nhất sao cho 2a là số lập phương và 5a là số chính phương.
Câu 3 (2,0 điểm).
Cho các số thực a, b, c thỏa mãn a, , b c  1 và 2 2 2
a + 4b + c + 2ab +12 = 3(a + 5b + c). Tìm giá 3 2 a a
trị nhỏ nhất của biểu thức T = +
a + (a + b) . 2 2 a + c
Câu 4 (7,0 điểm).
Cho tam giác ABC vuông tại A ( AB  AC ) nội tiếp đường tròn tâm O . Trên đường tròn (O)
lấy điểm D khác phía A so với đường thẳng BC (BD  AC). Qua B kẻ đường thẳng d song
song với CD . Đường thẳng d cắt đường thẳng AC tại E , cắt đường tròn (O) tại F ( F khác B ).
a) Gọi J là trung điểm của EC . Chứng minh rằng 4 điểm ,
A F, O, J cùng nằm trên một đường tròn.
b) Đường thẳng OE cắt đường thẳng AD tại I . Chứng minh rằng IBA = BDA.
c) Trên tia BD lấy điểm M sao cho BM = BA . Đường thẳng AM cắt đường thẳng DC tại N ,
đường thẳng BN cắt (O) tại K ( K khác B ). Gọi H là hình chiếu vuông góc của A trên BC .
Đường thẳng BD cắt các đường thẳng NH , CK lần lượt tại P, . Q 1 1 1 Chứng minh rằng = + . PM MQ BM
Câu 5 (2,0 điểm).
Cho một đa giác lồi có diện tích bằng 2
2024cm . Chứng minh rằng bao giờ cũng vẽ được trong đa
giác đó một tam giác có diện tích không nhỏ hơn 2 759cm . - HẾT - Trang 1
Họ và tên thí sinh: .... ... ...... ... ... ... ... ... ... ... ... ... ...... ... ... ... .. Số báo danh: ... ... ... ... ... ... ĐÁP ÁN
Câu 1 a) Giải phương trình 4 3 2
x − 4x + 6x − 4x − 3 = 0 . 2
Phương trình đã cho tương đương ( 2 x − x) + ( 2 2
2 x − 2x) − 3 = 0  ( 2 x − x − )( 2 2
1 x − 2x + 3) = 0 2
x − 2x −1 = 0   2
x − 2x + 3 = 0 Trường hợp 1. 2
x − 2x −1 = 0  x = 1 2. Trường hợp 2. 2
x − 2x + 3 = 0 (phương trình vô nghiệm).
Vậy nghiệm của phương trình là x = 1 2. 2
2x − x + y = 2y − x + 2x  ( )1
Câu 1b) Giải hệ phương trình (  2 − x + y 
) 2x +4 = 2 3x (2)
Đặt v = x + y (v  0). Phương trình ( ) 1 trở thành 2 2
2v − x = 2x − v
2x − v  0 
2x − v  0     2 2 2v − x =  (2x − v)2 2 2 5
 x − 4xv − v = 0
2x − v  0
2x − v  0   (   = − . x + v  )(x − v) v 5x 5 = 0  v = x
2x − v  0 x = 0 Trường hợp 1.  . v  0,v = 5
− x  x  0  2x − v  0  x = v = 0   . v = 5 − x y = 0
Thay vào (2) không thỏa mãn.
2x − v  0 Trường hợp 2.   x + y = .
x Thay vào (2) ta được phương trình v = x ( − x) x + = x  ( − x)2 2 ( 2x + ) 2 2 4 2 3 2
4 = 12x (0  x  2) Trang 2  (  4  4  2 x − 4x + 4)( 2 x + 4) 2
=12x  x + − 4 x + =12.     x  x  4 t = 6 Đặt t = x +
(t  4). Phương trình trở thành t(t − 4) =12   . x t = −2  (lo¹i) 4
x = 3 − 5 (tháa m·n) Với 2
t = 6  x + = 6  x − 6x + 4 = 0   . x x = 3 + 5  (lo¹i)
Vậy nghiệm của hệ phương trình là ( x; y) = (3 − 5; 11− 5 5).
Câu 2a. Tìm x  R sao cho x + 2024 và 1 − 2024 đều là các số nguyên. x
Đặt a = x + 2024  x = a − 2024 ; 1 b = − 2024 1
 = b + 2024 với a,b  Z x x 1 . x
= (a − 2024)(b + 2024) 1= ab −2024+ 2024 (a −b) x
 2 506 (a −b) = 2025 − abZ  a −b = 0
 2025 − ab = 0 và a = b
 a = b = 45  x = 45
 − 2024 . Thử lại ta có giá trị của x cần tìm là x = 4  5 − 2024 .
Câu 2b. Tìm số nguyên dương a nhỏ nhất sao cho 2a là số lập phương và 5a là số chính phương.
Vì 2a là số lập phương nên 3 2a = n ( * n  N )  n 2 *
 n = 2x, x N 3 3
 2a = 8x  a = 4x ( ) 1
Vì 5a là số chính phương nên 2 5a = k ( *
k  N )  k 5  k = 5y ( * y  N ) 2 2
 5a = 25y  a = 5y (2) (1), (2) 3 2 3
 4x = 5y  4x 5  x 5  x = m ( * 5 m  N ) 2 3 3
 a = 5y = 4.125.m = 500m  a = ( m)3 2 3 2 10 ; 5a = 50 m .
Vì a nhỏ nhất và 2 3
50 m là số chính phương nên m = 1  a = 500 (thỏa mãn). Vậy a = 500 . Trang 3 Câu 3.Cho các số thực a, b, c thỏa mãn a, , b c  1 và 2 2 2
a + 4b + c + 2ab +12 = 3(a + 5b + c). Tìm giá trị nhỏ nhất của biểu thức 3 2 a a T = +
a + (a + b) . 2 2 a + c
a + b + c + ab +
= (a + b + c)  (a + b)2 2 2 2 2 + c = − ( 2 4 2 12 3 5
3 b + 4) + 3(a + 5b + c)  (a + b)2 2 + c  1
− 2b + 3(a + 5b + c) = 3(a + b + c).
Kết hợp a + b + c  (a + b)2 2 2 + c    suy ra
(a +b)2 + c 
(a + b)2 + c   (a + b)2 2 2 2 3 2 + c  18 ( ) 1 .   3 a  a a a  1 1  +) Vì a  1 nên   T  + = a +  2 a  a
a + (a + b)2 2 a + c  a +  (a + b)2 2 a + c  4a 4a  9  1   = −    .
a + (a + b) 2 1 2 2 + a + c 2a +18  a + 9  5 2 b
 = 4,a + b = c a = 1 1  
minT =  a + (a + b)2 2
= a + c  b  = 2. 5 a =1 c = 3   
Cho tam giác ABC vuông tại A ( AB  AC ) nội tiếp đường tròn tâm O . Trên đường tròn (O)
lấy điểm D khác phía A so với đường thẳng BC (BD  AC) . Qua B kẻ đường thẳng d song
song với CD . Đường thẳng d cắt đường thẳng AC tại E , cắt đường tròn (O) tại F ( F khác B ).
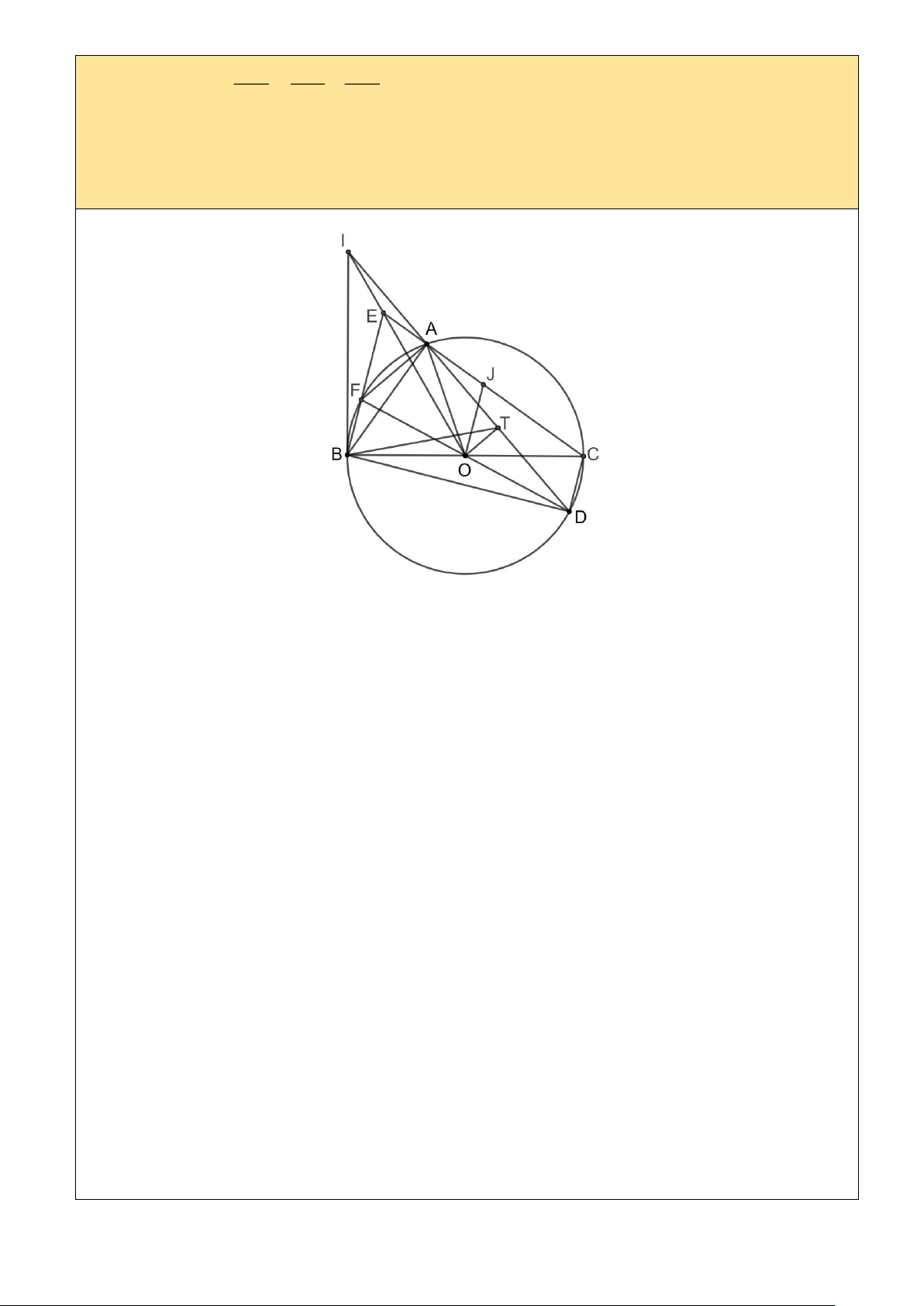
a) Gọi J là trung điểm của EC . Chứng minh rằng 4 điểm ,
A F, O, J cùng nằm trên một đường tròn.
b) Đường thẳng OE cắt đường thẳng AD tại I . Chứng minh rằng IBA = BDA.
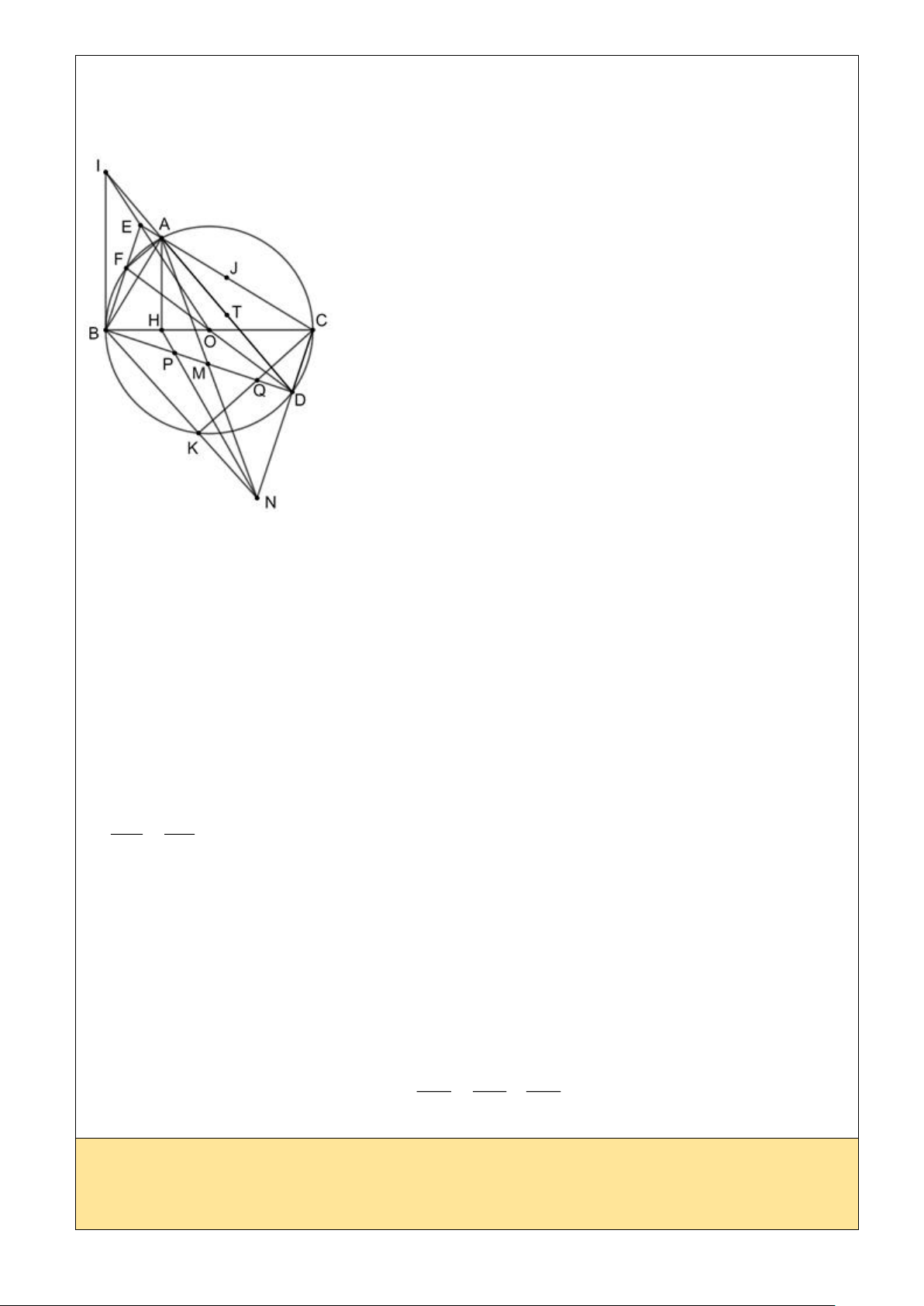
c) Trên tia BD lấy điểm M sao cho BM = BA . Đường thẳng AM cắt đường thẳng DC tại
N , đường thẳng BN cắt (O) tại K ( K khác B ). Gọi H là hình chiếu vuông góc của A
trên BC . Đường thẳng BD cắt các đường thẳng NH , CK lần lượt tại P, . Q Trang 4 1 1 1 Chứng minh rằng = + . PM MQ BM
a) Vì BFAC là tứ giác nội tiếp nên EAF = FBO (1)
Tam giác OBF cân nên BFO = FBO (2)
Vì OJ // BF nên BFO = FOJ (3)
(1), (2), (3) suy ra EAF = FOJ
 OJAF là tứ giác nội tiếp  ,
A F, O, J cùng thuộc một đường tròn.
b) Vì BF // CD nên EBC = BCD = BAD
 ABD ∽ BE  C (g-g) (*)
Lấy T là trung điểm của AD . Kết hợp O là trung điểm BC và (*) suy ra ABT  ∽ BEO   BOE = BTA
 BOTI là tứ giác nội tiếp.
Kết hợp OTI = 90 ( OT ⊥ AD )  IBO = 90 Trang 5
nên BI là tiếp tuyến của (O) .
Suy ra IBA = BDA. c) Ta có 2 2
BM = BA = BH.BC (4)
Tam giác BAM cân tại B nên
BAM = BMA = NMD (5)
BAM + MAC = NMD + MND = 90 (6)
(5), (6)  MAC = MNC  C
 AN cân tại C  2 2
CA = CN  CN = CA = CH.CB CN CB  =
 CNH ∽ CBN  CHN = CNB (7) CH CN
Mà CNB = CQD suy ra CHPQ là tứ giác nội tiếp (8)
(7), (8)  BH.BC = . BP BQ (9) Từ (4), (9) suy ra 2
BM = BP BQ = (BM − PM )(BM + MQ) 2 .
= BM + BM.MQ − PM.BM − PM.MQ 1 1 1
Suy ra BM.MQ = PM.BM + PM.MQ  = + PM MQ BM
Cho một đa giác lồi có diện tích bằng 2
2024cm . Chứng minh rằng bao giờ cũng vẽ được trong
đa giác đó một tam giác có diện tích không nhỏ hơn 2 759cm . Trang 6 C c d1 D E d d2 M N a A B
Vẽ đường thẳng a chứa cạnh AB của đa giác. Gọi C là đỉnh của đa giác mà khoảng cách từ
nó đến AB lớn nhất.
Qua C vẽ đường thẳng c song song với a .
Vẽ d , d , d là các đường thẳng song song với a sao cho d cách đều a và c ; d cách đều c 1 2 1
và d ; d cách đều 2 a và d .
Gọi 4h là khoảng cách giữa hai đường thẳng a và c .
Đường thẳng d1 cắt biên của đa giác tại D và E . Kéo dài hai cạnh của đa giác chứa D và E
cắt 2 đường thẳng c và d tạo thành hình thang hoặc tam giác có diện tích S = .2 ED h 1 .
Đường thẳng d2 cắt biên của đa giác tại M , N . Kéo dài hai cạnh của đa giác chứa M , N cắt
hai đường thẳng a và d tạo thành hình thang có diện tích S = MN.2h 2 .
Ta có hai hình nói trên bao toàn bộ đa giác
 S + S  2024  ED + MN .2h  2024 . 1 2 ( ) Ta có 1 S + S = MN h + ED h = MN + ED h  = CMN ADE ( ) 3 ( ) 3 .3 .3 .2 .2024 1518. 2 4 4 Vì S + S 1518 CMN ADE
nên một trong hai tam giác CMN hoặc ADE có diện tích lớn hơn hoặc bằng 2 759cm . Trang 7