Đề Thi Tuyển Sinh 10 Toán Chuyên Sở GD Quảng Bình 2025-2026 Có Đáp Án

SỞ GD&ĐT QUẢNG BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT Môn: TOÁN (CHUYÊN) ĐỀ CHÍNH THỨC SBD:…………..
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Đề có 01 trang gồm 5 câu Câu 1 (2,0 điểm)
a. Tính giá trị của biểu thức 3
A = 7 − 4 3 + 26 +15 3. a +1  a a 
b. Rút gọn biểu thức B = : + 
 với a  0 và a  4.
a − 4 a + 4  a − 2 a a − 2  Câu 2 (2,0 điểm) 2
x + x + y =1
a. Giải hệ phương trình  . 2
(x +1)(x + y −1) = −2
b. Cho phương trình 2 2
x + 2(m +1)x − m − 3 = 0 (m là tham số). Tìm tất cả các
giá trị của m để phương trình có hai nghiệm x  x thỏa mãn x − x + 5  2023. 1 2 1 2 Câu 3 (1,0 điểm)
Cho ba số thực dương x, y, z thỏa mãn x + y + z = 1. Chứng minh rằng: 1 1 1 1 + +   2 2 2
xy + 2z + 2z
yz + 2x + 2x
xz + 2y + 2y
xy + yz + zx Câu 4 (3,5 điểm)
Cho đường tròn (O) đường kính AB. Trên (O) lấy điểm C sao cho AC  BC (C
khác B). Các tiếp tuyến của (O) tại A và C cắt nhau tại M. Gọi H là giao điểm của
OM và AC, K là giao điểm thứ hai của BM với (O).
a. Chứng minh tứ giác AHKM nội tiếp.
b. Chứng minh HC là tia phân giác của góc KHB .
c. Qua O, kẻ đường thẳng song song với AM cắt MC tại P, MC cắt AB tại Q. AM MP Chứng minh rằng − =1. MP QP Câu 5 (1,5 điểm)
a. Tìm tất cả các số nguyên n sao cho 2
n + 2 chia hết cho n +1.
b. Tìm tất cả các cặp số nguyên dương ( ;
m n) biết rằng hai phương trình 2
x − 2mx − 3n = 0 và 2
x − 2nx − 3m = 0 (với x là ẩn) đều có nghiệm nguyên.
...........................HẾT.........................
SỞ GD&ĐT QUẢNG BÌNH HƯỚNG DẪN CHẤM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT Môn: TOÁN (CHUYÊN)
(Hướng dẫn chấm gồm có 05 trang) Yêu cầu chung
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu
cầu phải lập luận logic chặt chẽ, đầy đủ, chi tiết rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với
những bước sau có liên quan.
* Điểm thành phần của mỗi câu được phân chia đến 0,25 điểm. Đối với điểm là
0,5 điểm thì tùy tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Đối với Câu 4, học sinh không vẽ hình thì cho điểm 0. Trường hợp học sinh có vẽ
hình, nếu vẽ sai ở ý nào thì điểm 0 ở ý đó.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tùy theo mức điểm từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm
a. Tính giá trị biểu thức 3
A = 7 − 4 3 + 26 +15 3. 1 a +1  a a 
b. Rút gọn biểu thức B = : +   2,0
a − 4 a + 4  a − 2 a a − 2 
với a  0 và a  4. 3
A = 7 − 4 3 + 26 +15 3 a 0,5 = (2 − 3)2 + (2 + 3)3 3 = 2 − 3 + 2 + 3 = 4 0,5
Với a  0và a  4 ta có a +1  a a  B = :  +  0,25 2
( a − 2)  a( a − 2) a − 2  a +1  a a  = :  +  0,25 b 2 ( a − 2) a − 2 a − 2   a +1 a + a a +1 a − 2 = : =  0,25 2 2 ( a − 2) a − 2 ( a − 2) a( a +1) 1 =  0,25 a( a − 2) Câu Nội dung Điểm 2
x + x + y =1
a. Giải hệ phương trình  2
(x +1)(x + y −1) = −2 2
b. Cho phương trình 2 2
x + 2(m +1)x − m − 3 = 0 (m là tham số). 2,0
Tìm tất cả các giá trị của m để phương trình có hai nghiệm
x  x thỏa mãn x − x + 5  2023. 1 2 1 2 2 2
x + x + y =1
(x +1) + (x + y −1) =1 Ta có    0,25 2 2
(x +1)(x + y −1) = −2
(x +1)(x + y −1) = −2 2 u
 = x +1, (u  ) 1 u  + v =1 Đặt 
(*) ta được hệ phương trình  0,25
v = x + y −1 u  .v = 2 −  u  = 2  v = 1 −   0,25 a u  = 1 −  (L) v = 2
thay u = 2,v = −1 vào (*) ta có x =1  2 x +1 = 2 x = 1  y = 1 −     0,25
x + y −1 = −1 x + y = 0 x = 1 −  y =1
Vậy hệ phương trình có hai nghiệm (-1;1); (1;-1) Ta có 2 .
a c = −m − 3  0, m
  nên phương trình luôn có hai nghiệm
trái dấu, suy ra x  0  x . 0,5 1 2
Theo Vi et ta có x + x = 2( − m +1) b 1 2
Theo bài ra ta có x − x + 5  2023  −x − x − 5  2023 1 2 1 2 0,25  x + x  20 − 28  2 − m − 2  20 − 28 1 2 0,25
 2m  2026  m 1013. Vậy m 1013.
Cho ba số thực dương x, y, z thỏa mãn x + y + z = 1. Chứng minh 3 1 1 1 1 1,0 rằng: + +  . 2 2 2
xy + 2z + 2z
yz + 2x + 2x
xz + 2y + 2y
xy + yz + zx Ta có: 2 2
xy + 2z + 2z = xy + 2z + 2z(x + y + z) = (x + 2z)( y + 2z)
(xy + 2yz)(xy + 2xz) (xy + 2yz) + (xy + 2xz)2 2
(xy + yz + zx) 0,5 =  = xy 4xy xy Câu Nội dung Điểm 1 xy Suy ra  (1) 2 2
xy + 2z + 2z
(xy + yz + zx) Tương tự ta có 1 yz  (2) 2 2
yz + 2x + 2x
(xy + yz + zx) 0,25 1 zx  (3) 2 2
zx + 2y + 2y
(xy + yz + zx)
Cộng vế theo vế của các bất đẳng thức (1), (2), (3) ta được 1 1 1 + + 2 2 2
xy + 2z + 2z
yz + 2x + 2x
xz + 2y + 2y
xy + yz + zx 1  = 0,25
(xy + yz + zx)2 xy + yz + zx 1
Dấu bằng xảy ra khi và chỉ khi x = y = z = . 3
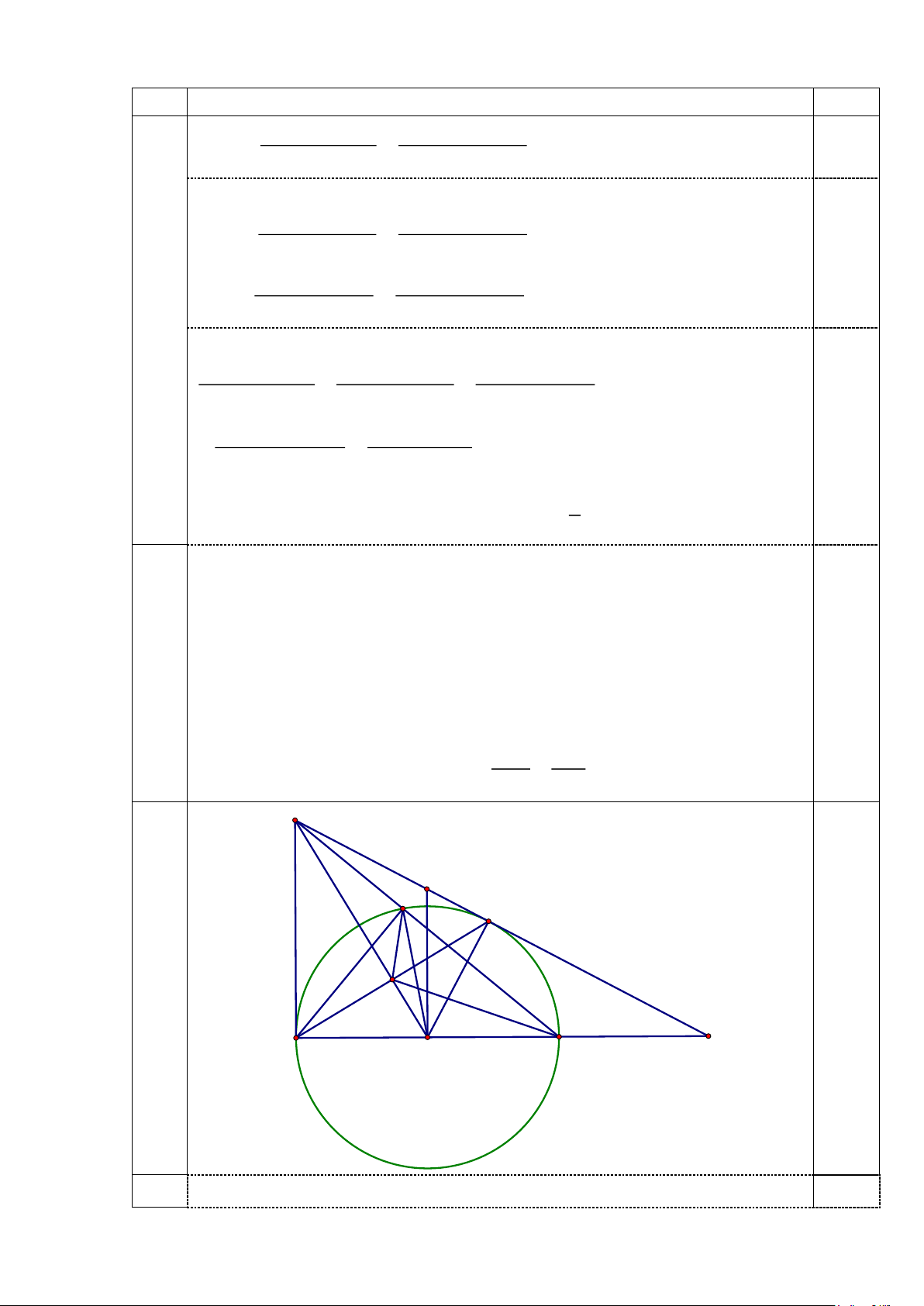
Cho đường tròn (O) đường kính AB. Trên (O) lấy điểm C sao cho
AC  BC (C khác B). Các tiếp tuyến của (O) tại A và C cắt nhau
tại M. Gọi H là giao điểm của OM và AC, K là giao điểm thứ hai
của BM với (O). 3,5 4
a. Chứng minh tứ giác AHKM nội tiếp. điểm
b. Chứng minh HC là tia phân giác của góc KHB .
c. Qua O, kẻ đường thẳng song song với AM cắt MC tại P, MC AM MP
cắt AB tại Q. Chứng minh rằng − =1. MP QP M P K C H A Q O B a Ta có 0
AKB = 90 (góc nội tiếp chắn nửa đường tròn) 0,5 Câu Nội dung Điểm Suy ra 0 AKM = 90 (1)
Lại có MH ⊥ AC (tính chất hai tiếp tuyến cắt nhau ) 0,5 nên 0 MHA = 90 (2)
Từ (1) và (2) suy ra tứ giác AHKM nội tiếp. 0,5
Ta có MHK = MAK (cùng chắn cung MK )
Và MAK = ABM (cùng chắn cung AK ) 0,25
Suy ra MHK = OBK (3) Ta thấy 0
KHO + OBK = KHO + MHK =180  BOHK nội tiếp. 0,25 b
Nên OHB = OKB (4)
Lại có OBK cân tại O nên OKB = OBK (5) 0,25
Từ (4) và (5) suy ra OHB = OBK (6)
Từ (3) và (6) suy ra MHK = OHB  KHC = BHC 0,25
Hay HC là tia phân giác của KHB .
Vì OP / / AM (GT ) nên AMO = MOP (hai góc so le trong)
Mà AMO = OMP (tính chất hai tiếp tuyến cắt nhau) 0,5
nên MOP = OMP (cùng bằng AMO )
Suy ra MOP cân tại P  MP = OP AM QM
Áp dụng định lý Ta-lét trong AMQ ta có = c OP QP
AM − OP QM − QP  = OP QP 0,5 AM MP AM MP  −1=  − =1 OP QP OP QP AM MP
mà MP = OP (chứng minh trên) nên − =1 (đpcm). MP QP
a. Tìm tất cả các số nguyên n sao cho 2
n + 2 chia hết cho n +1.
b. Tìm tất cả các cặp số nguyên dương ( ;
m n) biết rằng hai 1,5 5 phương trình 2
x − 2mx − 3n = 0 và 2
x − 2nx − 3m = 0 (với x là ẩn) điểm
đều có nghiệm nguyên. Ta có 2 2
n + 2 = n −1+ 3 = (n − ) 1 (n + ) 1 + 3. 0,25 a Vì 2 n + 2 (n + ) 1 mà (n − ) 1 (n + ) 1 (n + ) 1 nên 3 (n + ) 1 0,25 Suy ra n +1 3 − ; 1 − ;1;  3  n 4 − ; 2 − ;0;  2 0,25 Phương trình 2
x − 2mx − 3n = 0 ( ) 1 có 2
  = m + 3n . b 1 0,25 Phương trình 2
x − 2nx − 3m = 0 (2) có 2
  = n + 3m. 2 Câu Nội dung Điểm
Vì hai phương trình có nghiệm nguyên nên   ,   đều là số chính 1 2 phương.
Không mất tính tổng quát, giả sử m  n  0, khi đó
m  m + n  (m + )2  m + n = (m + )2 2 2 2 3 2 3
1  3n = 2m +1. 0,25
Do đó n là số lẻ. Đặt n = 2k +1 2
   = 4k +13k + 4 . 2
+) Nếu k 1;2;3; 
4 thì   không là số chính phương. 2
+) Nếu k = 0    = 4  m = n =1 (thỏa mãn). 2
+) Nếu k = 5 thì   =169  m =16,n =11 (thỏa mãn). 2 0,25
+ Nếu k  5 thì ( k + )2  k + k +  ( k + )2 2 2 3 4 13 4 2 4    không là 2 số chính phương. Vậy các bộ số ( ;
m n) thỏa mãn là: (1; ) 1 , (16;1 ) 1 , (11;16) .
...........................HẾT.........................