Đề Thi Tuyển Sinh 10 Toán Chuyên Sở GD Sơn La 2025-2026 Có Đáp Án

SỞ GD&ĐT SƠN LA
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
Môn thi: TOÁN (dành cho chuyên Toán, Tin) ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian phát đề
(Đề thi có 01 trang)
x y + x − y x − y
Câu 1. (1,0 điểm) Cho biểu thức Q =
với x  0; y  0. 1+ xy
a) Rút gọn biểu thức Q.
b) Tính giá trị biểu thức Q khi x = 2024 + 2 2023; y = 2024 − 2 2023.
Câu 2. (1.0 điểm) Cho parabol 2
(P) : y = x và đường thẳng (d) : y = (2m − 3)x+3m − 5 (m là tham số).
a) Xác định giá trị của m để đường thẳng (d) đi qua điểm ( A −2;3).
b) Tìm m để đường thẳng (d) tiếp xúc với parabol (P).
Câu 3. (1,0 điểm)
Hai đội thanh niên tình nguyện cùng làm chung một công việc thì hoàn thành trong 6
giờ. Nếu hai đội làm riêng thì thời gian hoàn thành công việc của đội thứ hai ít hơn thời gian
hoàn thành công việc của đội thứ nhất là 5 giờ. Hỏi nếu làm riêng thì mỗi đội hoàn thành công việc trong bao lâu?
Câu 4. (1,0 điểm)
Tìm tất cả các giá trị của tham số m để phương trình 2 2
x − 2m x + m − m +1 = 0 có hai
nghiệm x , x thỏa mãn 2 2
x − x + 4m x = 16 . 1 2 2 1 1
Câu 5. (1,0 điểm) Giải phương trình: 2 2
x − 4x + x − 4x − 5 = 7. 2 2
x + xy − 2y = x + 2y
Câu 6. (1,0 điểm) Giải hệ phương trình:  . 3 2 2 2
x + 2x y = x + y −1
Câu 7. (3,5 điểm)
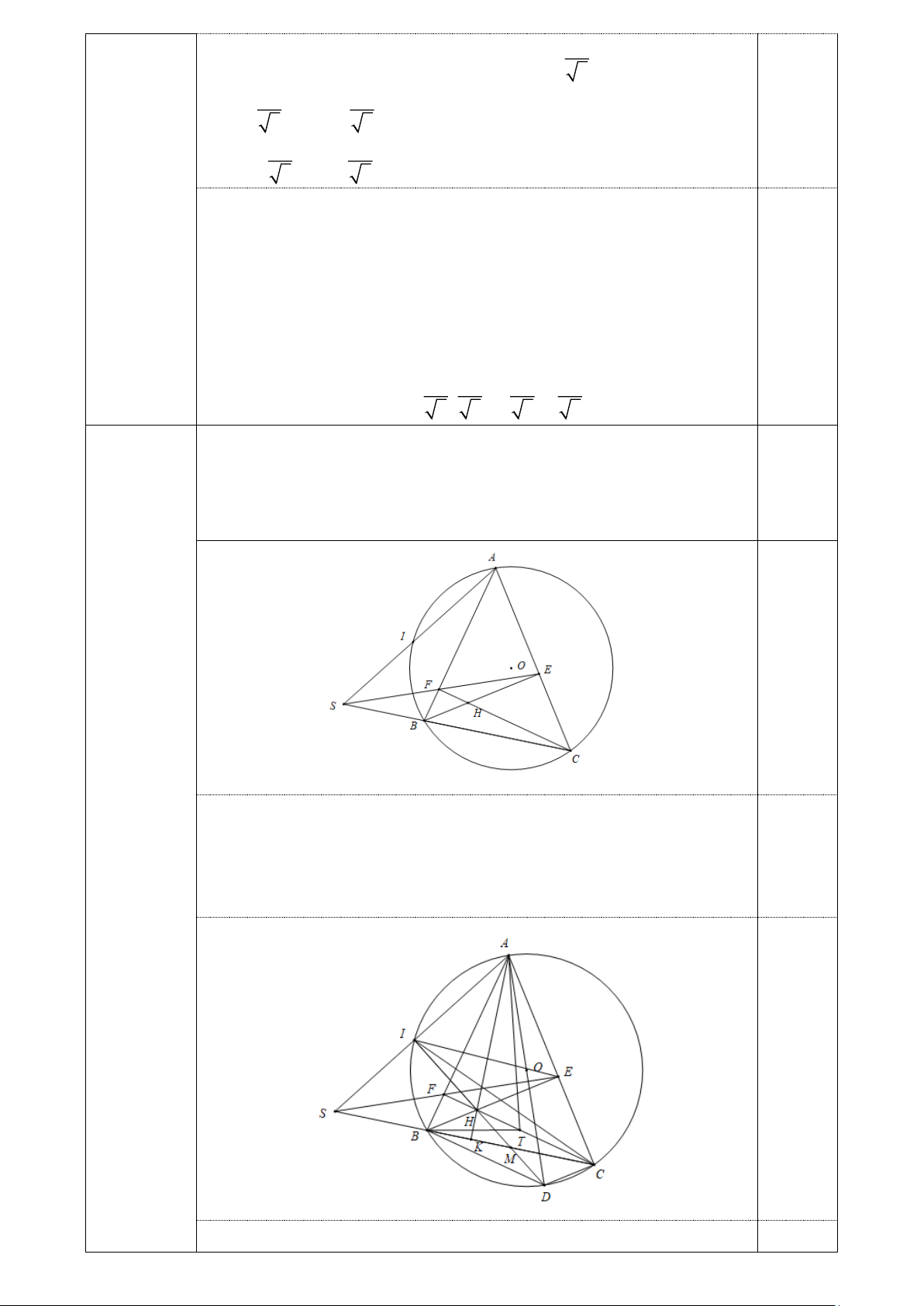
Cho tam giác ABC nhọn (AB  AC) nội tiếp đường tròn (O), các đường cao BE và
CF cắt nhau tại H. Gọi S là giao điểm của đường thẳng BC và EF; I là giao điểm của
SA và đường tròn (O) (với I khác A ).
a) Chứng minh rằng tứ giác AFHE là tứ giác nội tiếp.
b) Chứng minh SF.SE = SI.SA và HI ⊥ . SA
c) Gọi M là trung điểm của BC, kẻ đường kính AD của (O). Chứng minh ba điểm
H , M , D thẳng hàng và H là trực tâm tam giác ASM .
d) Giả sử T là điểm nằm trên đoạn thẳng HC sao cho AT vuông góc với BT.
Chứng minh hai đường tròn ngoại tiếp của tam giác IST và tam giác ECT tiếp xúc với nhau.
Câu 8. (0,5 điểm) Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz . Chứng minh rằng: 2 2 2 1+ 1+ x 1+ 1+ y 1+ 1+ z + +  . xyz x y z
-------------Hết-------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………………….. Số báo danh:…………… Trang 1
SỞ GD&ĐT SƠN LA HƯỚNG DẪN CHẤM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 ĐỀ CHÍNH THỨC
Môn thi: Toán chuyên (HD có 04 trang) Câu Hướng dẫn chấm Điểm
x y + x − y x − y Cho biểu thức Q =
(x  0; y  0). 1+ xy 1,0
a) Rút gọn biểu thức Q. xy + − −
( x − y)+( x − y x y x y x y ) Q = = 1+ xy 1+ xy 0,5
( xy + )1( x − y) = = x − y Câu 1 1+ xy
b) Tính giá trị biểu thức với x =2024+ 2 2023; y =2024 − 2 2023
Q = 2024 + 2 2023 − 2024 − 2 2024 0,5 = ( 2023 + )2 1 − ( 2023 − )2 1 = 2023 +1− 2023 +1 = 2 Cho parabol 2
(P) : y = x và đường thẳng (d) : y = (2m − 3)x+3m − 5 (m là tham số). 1,0
a) Xác định giá trị của m để đường thẳng (d) đi qua điểm ( A −2;3).
Đường thẳng (d) đi qua điểm ( A −2;3) nên ta có: 0,5 (2m −3).( 2) − + 3m − 5 = 3
 − m + + m − = 4 6 3 5 3
 −m = 2  m = 2 −
b) Tìm m để đường thẳng (d) tiếp xúc với parabol (P). Câu 2
Phương trình hoành dộ giao điểm 2
x − (2m − 3)x − 3m + 5 = 0 (*) 0,5
 = − m − 2 2 2 ' (2 3) − 4( 3
− m + 5) = 4m −12m + 9 +12m − 20 = 4m −11
Đường thẳng (d) tiếp xúc với parabol (P)  phương trình (*) có nghiệm kép 11 2
4m −11 = 0  m =  . 2
Hai đội thanh niên tình nguyện cùng làm chung một công việc thì
hoàn thành trong 6 giờ. Nếu hai đội làm riêng thì thời gian hoàn
thành công việc của đội thứ hai ít hơn thời gian hoàn thành công 1,0
việc của đội thứ nhất là 5 giờ. Hỏi nếu làm riêng thì mỗi đội hoàn
thành công việc trong bao lâu? Câu 3
Gọi thời gian đội thứ nhất làm riêng và hoàn thành là x giờ (x  6)
Thời gian đội thứ hai làm làm riêng và hoàn thành là 0,5 x − 5 giờ Trang 2
Một giờ cả hai đội làm được 1 1 + công việc x x − 5
Theo bài ra ta có phương trình 1 1 1 + = x x − 5 6
 6(x − 5) + 6x = x(x − 5) 2
 x −17x + 30 = 0  0,5 x = 15 (t/m)  x = 2 (loai)
Vậy đội một làm riêng hoàn thành công việc sau 15 giờ và
thời gian đội hai hoàn thành riêng là 10 giờ.
Tìm tất cả các giá trị của tham số m để phương trình 2 2
x − 2m x + m − m +1 = 0 có hai nghiệm
x , x thỏa mãn 1,0 1 2 2 2
x − x + 4m x = 16 . 2 1 1 Ta có: 2 2 2 2
 ' = m − (m − m +1) = m − m + m −1 = m −1 Để phương trình 2 2
x − 2m x + m − m +1 = 0 có hai nghiệm x , x thì 0,5 1 2 Câu 4  '  0
 m −1  0  m  1.
x + x = 2m Theo định lí viet: 1 2  2
x .x = m − m +1  1 2 Mặt khác: 2 2 2 2
x − x + 4m x = 16  x − x + 2(x + x ) x = 16 2 1 1 2 1 1 2 1 2 2 2 2 2
 x − x + 2x + 2x .x =16  x + x + 2x .x =16 2 1 1 1 2 2 1 1 2 0,5 m = 2 (t/m) 2 2 2
 (x + x ) =16  (2m) =16  m = 4  1 2  m = 2 − (loai) KL:
Giải phương trình: 2 2
x − 4x + x − 4x − 5 = 7. 1,0 Điều kiện: 2
x − 4x − 5  0 (*) hay ( x  1 − ; x  5) Phương trình 0,5 2 2 2 2
x − 4x + x − 4x − 5 = 7  x − 4x − 5 + x − 4x − 5 − 2 = 0 Câu 5 Đặt 2
t = x − 4x − 5 (t  0) ta được phương trình 2 t + t − 2 = 0 t =1 (t/m) Giải phương trình 2
t + t − 2 = 0   t = 2 − (loai) Với t = 1 ta có 2
x − 4x − 5 =1 0,5 x = 2 + 10 2 2
 x − 4x − 5 = 1  x − 4x − 6 = 0   (t/m (*)) x = 2 − 10 KL: 2 2
x + xy − 2y = x + 2y (1)
Giải hệ phương trình:  . 1,0 3 2 2 2
x + 2x y = x + y −1 (2) Phương trình (1) 2 2
 x + 2xy − xy − 2y = x + 2y
 x(x + 2y) − y(x + 2y) = x + 2y
 (x + 2y)(x − y −1) = 0 0,5 x + 2y = 0 x = 2 − y    
x − y −1 = 0 x = y +1
+) Với x = −2y thế vào (2) ta có: Trang 3 1 3 3 2 2 2 8
− y + 8y = 4y + y −1  5y =1  y =  Câu 6 5 1 2 + ) y =  x = − 5 5 1 2 0,25 +)y = −  x = 5 5 +) Với x = y +1 thế vào (2) ta có: ( y + )3 2 2 2
1 + 2( y +1) .y = ( y +1) + y −1 0,25  ( y + ) 2
1 (3y + 2y +1) = 0  y = 1 −   2
3y + 2y +1 = 0 (VN)
Với y = −1 x = 0 KL: Hệ có ba nghiệm  2 1   2 1  − ; ; ;− ;(0;−     ) 1 .  5 5   5 5 
Cho tam giác ABC nhọn (AB  AC) nội tiếp đường tròn (O),
các đường cao BE và CF cắt nhau tại H. Gọi S là giao điểm 3,5
của đường thẳng BC và EF; I là giao điểm của SA và đường
tròn (O) (với I khác A ). 0,5
a) Chứng minh rằng tứ giác AFHE là tứ giác nội tiếp. Ta có: 0 0,5
BEA = CFA = 90 (giả thiết) 0
 HEA = HFA = 90 hay 0 HEA + HFA = 180
 tứ giác AFHE nội tiếp. Câu 7
b) Chứng minh SF.SE = SI.SA và HI ⊥ . SA Trang 4
* Chứng minh SF.SE = SI.SA
Tứ giác BCEF nội tiếp (vì có hai đỉnh E và F cùng nhìn BC dưới một góc vuông)
 SFB = BCE (cùng bù với BFE) hay  SFB = SCE Có FSB = CSE  SFB  SC  E ( g.g) 0,5 SF SB  =
 SF.SE = S . B SC (1) SC SE
Ta lại có: IAB = ICB (cùng chắn cung IB của (O) ) hay SAB = ICS  SBA  SIC 
( SAB = ICS và S chung) SA SB  =
 SI.SA = S . B SC (2) SC SI
Từ (1) và (2)  SF.SE = SI.SA *Chứng minh HI ⊥ . SA SF SA
Do SF.SE = SI.SA  =  SIE  SFA  SI SE
 IAF = IEF mà IAF, IEF cùng nhìn cạnh IF nên tứ giác AIFE nội tiếp đường tròn. 0,5
Mặt khác: tứ giác AFHE nội tiếp (câu a).
Hay các điểm I, A, E, H, F cùng thuộc một đường tròn.
Tứ giác AIHE nội tiếp đường tròn mà o o
HEA = 90  HIA = 90  HI ⊥ SA .
c) Gọi M là trung điểm của BC, kẻ đường kính AD của (O).
Chứng minh ba điểm H , M , D thẳng hàng và H là trực tâm tam giác ASM . 0,5 Câu 7
* Chứng minh ba điểm H , M , D thẳng hàng
M là trung điểm của BC và AD là đường kính nên ta có:
BH CD (cùng ⊥ AC) và CH BD (cùng ⊥ AB)
 tứ giác BHCD là hình bình hành
 BC và DH cắt nhau tại trung điểm M của mỗi đường hay
H , M , D thẳng hàng (3)
*Chứng minh H là trực tâm tam giác ASM .
Ta có: IH ⊥ IA (câu b) và DI ⊥ IA (góc o
AID = 90 )  DI  IH
hay H , I, D thẳng hàng (4) Từ (3) và (4)  0,5
M , D, H , I thẳng hàng  MH ⊥ SA (5)
Mặt khác: AH ⊥ BC (AH là đường cao thứ 3 của tam giác ABC) (6)
Từ (5) và (6)  H là trực tâm ASM .
d) Giả sử T là điểm nằm trên đoạn thẳng HC sao cho AT
vuông góc với BT. Chứng minh hai đường tròn ngoại tiếp của
tam giác ITS và tam giác ECT tiếp xúc với nhau. 0,5 Ta chứng minh được 2
AT = AI.AS  AT là tiếp tuyến của đường tròn ngoại tiếp Trang 5 I  ST (7) 2
AT = AE.AC  AT là tiếp tuyến của đường tròn ngoại tiếp ECT  (8)
Từ (7) và (8)  AT là tiếp tuyến chung hay hai đường tròn
hay hai đường tròn ngoại tiếp của tam giác ITS và tam giác
ECT tiếp xúc với nhau.
Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz . Câu 8 2 2 2 0,5
Chứng minh rằng:1+ 1+ x 1+ 1+ y 1+ 1+ z + +  xyz (*) x y z Ta có: 1 1 1
x + y + z = xyz  + + =1 yz zx xy 2 2 2 1+ 1+ x 1+ 1+ y 1+ 1+ z VT(*) = + + x y z 2 2 2 1 1 1 1+ x 1+ y 1+ z = + + + + + + 2 2 2 x y z x y z Xét 1 1 1 1 1 +1 = + + + 2 2 x x yz zx xy
 1 1  1 1  1  2 1 1  = + +  + +    
 (dầu bằng xảy ra khi 0,5
 x y  x z  2  x y z  y = z) Tương tự: 1 1  2 1 1  +1  + +
(dầu bằng xảy ra khi z = x) 2   y 2  y x z  1 1  2 1 1  +1  + +
(dầu bằng xảy ra khi y = x) 2   z 2  z y x 
 1 1 1  1  2 1 1 2 1 1 2 1 1  VT (*)  + + + + + + + + + + +    
 x y z  2  x y z y z x z x y   1 1 1   3 + +    x y z   
Vậy ta phải chứng minh 1 1 1 3 + +  xyz    x y z  2
 3(xy + yz + zx)  (xyz) 2
 3(xy + yz + zx)  (x + y + z) 2 2 2
 3(xy + yz + zx)  x + y + z + 2(xy + yz + zx) 2 2 2
 xy + yz + zx  x + y + z 2 2 2
 2(xy + yz + zx)  2(x + y + z ) 2 2 2
 (x − y) + (y − z) + (z − x)  0
Dấu bằng xảy ra x = y = z = 3
Chú ý: Các cách giải khác đúng được chấm tối đa số điểm tương ứng với từng nội dung. Trang 6