Đề Thi Tuyển Sinh 10 Toán Chuyên Sở GD Tuyên Quang 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH VÀO LỚP 10 THPT TUYÊN QUANG
Môn thi: Toán chuyên ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
(Đề thi có 01 trang)
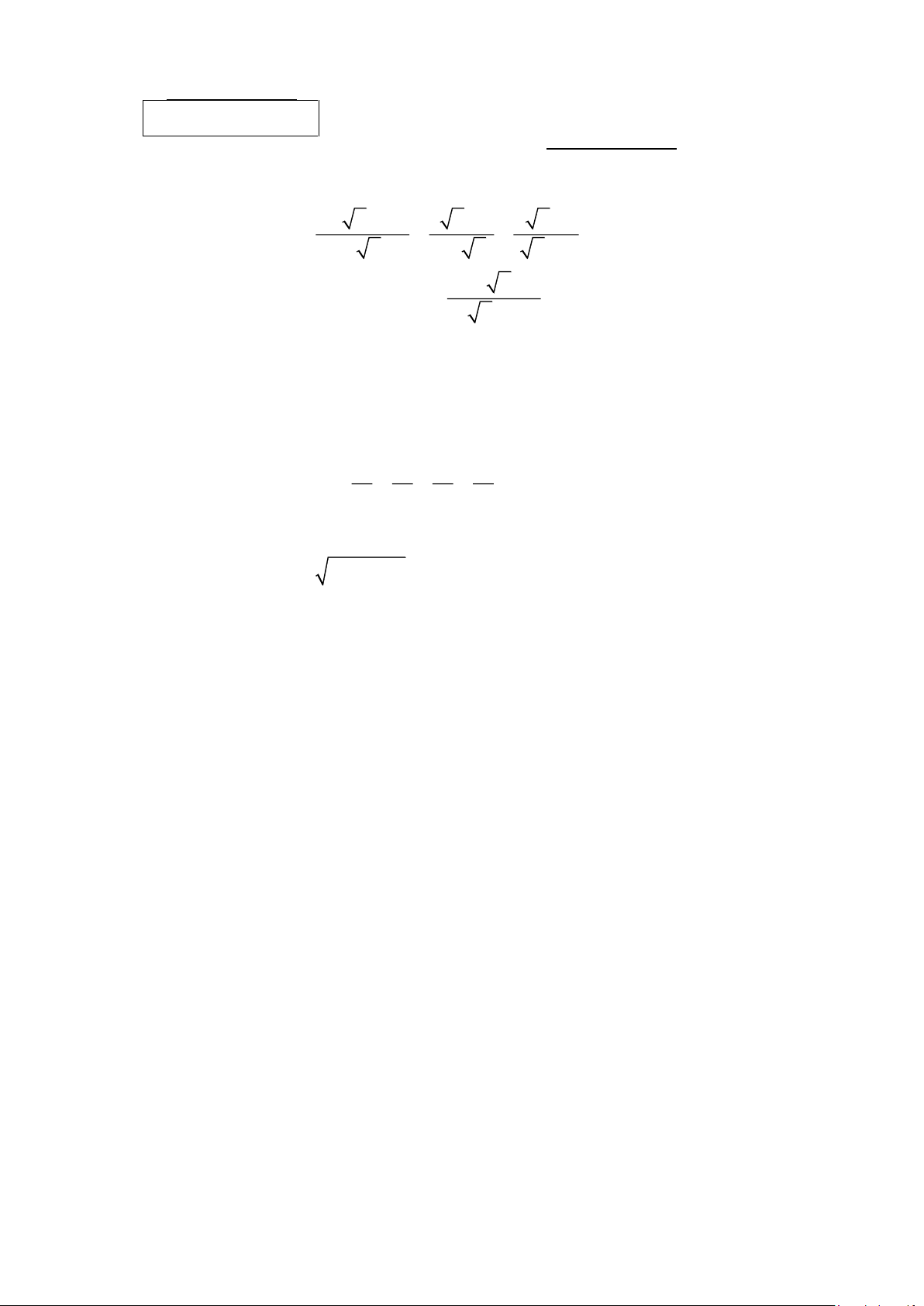
Câu 1 (2,0 điểm) 15 x −11
3 x − 2 2 x + 3
a) Rút gọn biểu thức P = + −
với x  0, x  1. x + 2 x − 3 1− x x + 3 a − 3 a + 6
b) Tìm giá trị nhỏ nhất của biểu thức Q = với a  4. a − 2
Câu 2 (3,0 điểm) 1. Cho phương trình 4 2
x − 4x + m + 2 = 0 (1), với m là tham số.
a) Giải phương trình (1) khi m = −7.
b) Tìm m để phương trình (1) có 4 nghiệm phân biệt x , x , x , x thỏa mãn 1 2 3 4 1 1 1 1 + + + = 2x x x x . 2 2 2 2 1 2 3 4 x x x x 1 2 3 4 2 2
2x + y + 3xy − 3x − 9 = 0 
2. Giải hệ phương trình  . 2
 x − y + 3 = 2x + y 
Câu 3 (3,0 điểm). Cho tam giác tù ABC có 0
ABC  90 nội tiếp đường tròn (O). Tiếp tuyến
tại C của (O) cắt đường thẳng AB tại S. Lấy điểm P thuộc miền trong tam giác OAC sao cho SC = .
SP Đường thẳng SP cắt (O) tại hai điểm E, F (E ở giữa S và F). Các đường
thẳng AP, BP cắt lại (O) lần lượt tại K, .
L Chứng minh rằng:
a) Tam giác ACS đồng dạng với tam giác CBS; b) APS = PBS;
c) Tứ giác EKLF là hình thang cân.
Câu 4 (1,0 điểm)
a) Chứng minh rằng 2023 2 A = 2
+ 3m + 6n − 23 chia hết cho 3 với mọi số tự nhiên m, . n
b) Tìm tất cả các cặp số tự nhiên (m, n) để 2 3m +6n−22 B = 3
+ 4 là một số nguyên tố.
Câu 5 (1,0 điểm). Ban đầu, trên bảng có n số nguyên dương đầu tiên được viết liên tiếp từ
trái qua phải: 1, 2, 3,..., n −1, .
n Ta thực hiện trò chơi đổi số như sau: Mỗi lượt chơi, lấy ba số
đứng liền nhau a, b, c và đổi chỗ a với c thành c, b, .
a Hỏi sau hữu hạn lượt chơi như trên ta
có thể thu được dãy số ngược lại n, n −1,..., 2, 1 hay không, nếu:
a) n = 5;
b) n = 2024. -----HẾT-----
Ghi chú: Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………………….………………Số báo danh:……………….. Trang 1
HƯỚNG DẪN CHẤM ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT Môn: Toán chuyên
(Hướng dẫn này có 04 trang) ----------
Câu 1 (2,0 điểm) 15 x −11
3 x − 2 2 x + 3
a) Rút gọn biểu thức P = + −
với x  0, x  1. x + 2 x − 3 1− x x + 3 Hướng dẫn chấm Điểm 15 x −11 2 − 3 x 2 x + 3 Ta có P = ( + − 0,25 x − ) 1 ( x + 3) x −1 x + 3
15 x −11+ (2 − 3 x )( x + 3) − (2 x + 3)( x − ) 1 = ( 0,25 x − ) 1 ( x + 3) 5
− x + 7 x − 2 = ( 0,25 x − ) 1 ( x + 3)
( x − )1( 5− x +2) 5− x +2 = ( = 0,25 x − ) 1 ( x + 3) . x + 3 a − 3 a + 6
b) Tìm giá trị nhỏ nhất của biểu thức Q = với a  4. a − 2 Hướng dẫn chấm Điểm a − 3 a + 6 4 Ta có Q = = a −1+ 0,25 a − 2 a − 2  4  = a − 2 + +1.   0,25  a − 2 
Với a  4 thì a − 2  0. Áp dụng Bất đẳng thức AM-GM (Côsi) ta được 0,25 Q  ( a − ) 4 2 2 . +1 = 5. a − 2
Q = 5 chẳng hạn khi a = 16. Vậy min Q = 5. 0,25
Câu 2 (3,0 điểm) 1. Cho phương trình 4 2
x − 4x + m + 2 = 0 (1), với m là tham số.
a) Giải phương trình (1) khi m = −7.
b) Tìm tất cả các giá trị của m để phương trình (1) có 4 nghiệm phân biệt x , x , x , x thỏa 1 2 3 4 mãn 1 1 1 1 + + + = 2x x x x . 2 2 2 2 1 2 3 4 x x x x 1 2 3 4 Trang 2 Hướng dẫn chấm Điểm
a) Với m = −7, ta có phương trình 4 2
x − 4x − 5 = 0. 0,25 Đặt 2
t = x (t  0), ta được 2
t − 4t − 5 = 0 (*). 0,25
Giải phương trình (*) ta được t = −1 (loại) và t = 5 (thỏa mãn). 0,25
Với t = 5 ta được 2
x = 5  x =  5. Vậy phương trình hai nghiệm x =  5. 0,25 b) Đặt 2
t = x (t  0) , ta được phương trình 2
t − 4t + m + 2 = 0 (**).
Phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi phương trình (**) có hai nghiệm 0,25
phân biệt t  0, t  0. 1 2   0 4 − (m + 2)  0  
Điều này tương đương với t
 + t  0  2  0  2 −  m  2 (a). 1 2 0,25 t  t  0 m + 2  0  1 2  1 1 1 1 2 2 Theo bài ra + + + = 2x x x x  +
= 2t t  t + t = t t (b). 2 2 2 2 ( )2 1 2 3 4 1 2 1 2 1 2 0,25 x x x x t t 1 2 3 4 1 2 Theo Viet thì 2
(b)  4 = (m + 2)  m = 4
− (loại) và m = 0 (thỏa mãn). 0,25
Vậy m = 0 là giá trị duy nhất cần tìm. 2 2
2x + y + 3xy − 3x − 9 = 0 
2. Giải hệ phương trình  . 2
 x − y + 3 = 2x + y  Hướng dẫn chấm Điểm Điều kiện xác định: 2
x − y + 3  0 (*). Ta có 0,25 2 2
2x + y + 3xy − 3x − 9 = 0  (x + y − 3)(2x + y + 3) = 0
x + y − 3 = 0  .  0,25
2x + y + 3 = 0
Với y + x − 3 = 0  y = −x + 3, thay vào phương trình 2
x − y + 3 = 2x + y ta được x  3 x + 3  0 −   0,25 2 9 24
x + x = x + 3      = −  = x + x =  ( x y x + 3) 9 . 2 2 x = − 5 5  5
Với 2x + y + 3 = 0  2x + y = 3
− , thay vào phương trình 2
x − y + 3 = 2x + y ta được 0,25 2 x + 2x + 3 = 3 − , vô nghiệm.  9 x = − 
Vậy hệ phương trình có nghiệm duy nhất 5  . 0,25 24 y =  5 Trang 3
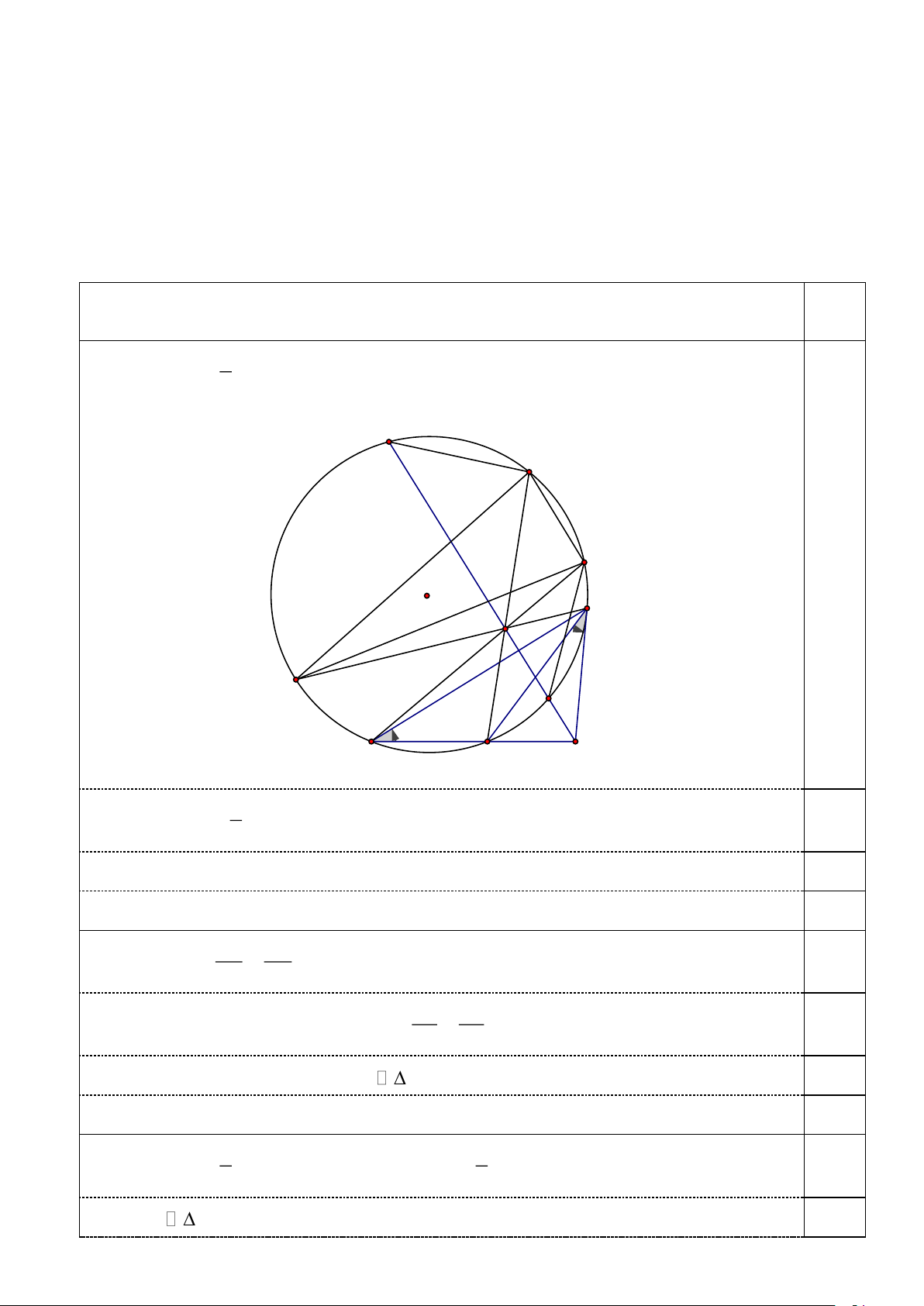
Câu 3 (3,0 điểm). Cho tam giác tù ABC có 0
ABC  90 nội tiếp đường tròn (O). Tiếp tuyến
tại C của (O) cắt đường thẳng AB tại S. Lấy điểm P thuộc miền trong tam giác OAC sao cho SC = .
SP Đường thẳng SP cắt (O) tại hai điểm E, F (E ở giữa S và F). Các đường
thẳng AP, BP cắt lại (O) lần lượt tại K, .
L Chứng minh rằng:
a) Tam giác ACS đồng dạng với tam giác CBS; b) APS = PBS;
c) Tứ giác EKLF là hình thang cân. Hướng dẫn chấm Điể m 1
a) Ta có CAS = sđCEB (a). 2 F n L K 0,25 O C P M E m A B S 1
Mặt khác BCS = sđCEB (b). 0,25 2
Từ (a) và (b) suy ra BCS = CAS (1). 0,25
Từ (1) và ASC = BSC suy ra hai tam giác ACS và CBS đồng dạng. 0,25 CS AS b) Từ a) suy ra 2 =  SC = S . B SA (c). 0,25 BS CS SP SA
Vì SC = SP nên 2
(c)  SP = S . B SA  = (d). 0,25 SB SP
Từ (d) và PSA = BSP suy ra PSA   . BSP 0,25
Do đó APS = PBS. 0,25 1 1
c) Ta có BPS = (sđBmE + sđLnF) và PAS = (sđBmE + sđECK ) (e). 0,25 2 2 Vì PSA  BSP 
nên BPS = PAS. Kết hợp với (e) suy ra sđLnF = sđECK (f). 0,25 Trang 4 Từ (f) suy ra 1 1 1
LFE + FLK = sđLKE + sđFAK = (sđLnF + sđLtK) 1 0
+ sđFAK = 180  LK // EF. 0,25 2 2 2 2
Do đó EKLF là hình thang. Hơn nữa sđLnF = sđECK  FL = KE  EKLF là hình 0,25 thang cân.
Câu 4 (1,0 điểm)
a) Chứng minh rằng 2023 2 A = 2
+ 3m + 6n − 23 chia hết cho 3 với mọi số tự nhiên m, . n Hướng dẫn chấm Điểm Ta có 2023 2  1 − (mod3)  2  1 − (mod3). 0,25 Suy ra 2023 2 A = 2
+ 3m + 6n − 23  1 − − 23  0 (mod3). 0,25
b) Tìm tất cả các cặp số tự nhiên (m, n) để 2 3m +6n−22 B = 3
+ 4 là một số nguyên tố. Hướng dẫn chấm Điểm Nếu 2
X = 3m + 6n − 22  0 thì B  , do đó 2
X = 3m + 6n − 22  0. Ta có X = ( 2
3 m + 2n − 8) + 2  X  2 (mod3)  X = 3k + 2 (k  ). Do đó 0,25 3k +2 = 3 + 4 = 9.27k B
+ 4  9.1+ 4  0 (mod13)  B =13. Từ B = 13 suy ra 2 2 m  8 m = 0 m = 0 2 2
k = 0  3m + 6n − 22 = 2  m + 2n − 8 = 0      .  2 0,25 m 2 m = 4 m = 2 Vậy cặp số
cần tìm là (0,4) , (2,2) .
Câu 5 (1,0 điểm). Ban đầu, trên bảng có n số nguyên dương đầu tiên được viết liên tiếp từ trái
qua phải: 1, 2, 3,..., n −1, .
n Ta thực hiện trò chơi đổi số như sau: Mỗi lượt chơi, lấy ba số đứng
liền nhau a, b, c và đổi chỗ a với c thành c, b, .
a Hỏi sau hữu hạn lượt chơi như trên ta có
thể thu được dãy số ngược lại n, n −1,..., 2, 1 hay không, nếu:
a) n = 5; b) n = 2024. Hướng dẫn chấm Điểm
a) Với n = 5 ta thực hiện các bước biến đổi như sau: 1 2 3 4 5 1 4 3 2 5 0,5 3 4 1 2 5 3 4 5 2 1 5 4 3 2 1
b) Với n = 2024 : Ta thấy rằng với cách đổi như trên thì các số lẻ luôn ở vị trí lẻ còn số 0,25
chẵn luôn ở vị trí chẵn.
Ban đầu số 2024 ở vị trí chẵn, do đó nó không thể chuyển về vị trí đầu tiên trong dãy số 0,25
2024, 2023,…, 2, 1 được. Trang 5 -----Hết-----
Ghi chú: Nếu thí sinh làm bài theo cách khác thì vẫn cho điểm theo các phần đúng tương ứng. Trang 6