Đề Thi Tuyển Sinh 10 Toán Chuyên Sở GD Vĩnh Long 2025-2026 Có Đáp Án

SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN VĨNH LONG
Môn: TOÁN (Chuyên)
Thời gian làm bài: 150 phút (không kể thời gian giao đề) Câu 1. (2,0 điểm) 2
a) Tính giá trị biểu thức A = 4 + 2 3 + 6 − 2 5 + . 5 + 3  1 2 x   2 x 
b) Cho biểu thức P =  −  :1−  
với x  0; x  1 Rút gọn biểu
x −1 x x + x − x −1  x 1  +     thức P . Câu 2. (1,0 điểm)
Tìm tất cả các giá trị m của để phương trình 2
x − 5x + 3m +1 = 0 ( x là ẩn số; m là tham
số) có hai nghiệm phân biệt x ; x x − x = 15 . 1 2 thỏa mãn 2 2 1 2 Câu 3. (1,5 điểm)  x y 5 − = 
a) Giải hệ phương trình y x 6   2 2 x − y = 5
b) Giải phương trình ( x − )4 2
1 = x − 2x + 3 . Câu 4. (1,5 điểm)
a) Tìm tất cả các số nguyên x sao cho giá trị của biểu thức 2
x + x + 6 là một số chính phương.
b) Tìm nghiệm nguyên của phương trình 2 y = − ( 6 3
2 x − x y − 32). Câu 5. (3,0 điểm)
Cho tam giác nhọn ABC ( AB  AC) nội tiếp đường tròn (O) . Kẻ đường cao AH của
tam giác ABC ( H thuộc BC ). Gọi P;Q lần lượt là chân của đường vuông góc kẻ từ H
đến các cạnh AB, AC .
a) Chứng minh PQH = BAH .
b) Hai đường thẳng PQ và BC cắt nhau tại M . Chứng minh M  QH ∽ M  HP và 2 MH = . MB MC .
c) Đường thẳng MA và cắt đường tròn (O) tại K ( K khác A ). KH cắt đường tròn (O)
tại D ( D khác K ) . Gọi J là trung điểm của HD . Chứng minh JQ = JC . Câu 6. (1,0 điểm) 2 x +10
Tìm giá trị nhỏ nhất của biểu thức . 2 x + 9
---------------------------------@Hết@--------------------------------- Trang 1 HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm) 2
a) Tính giá trị biểu thức A = 4 + 2 3 + 6 − 2 5 + . 5 + 3  1 2 x   2 x 
b) Cho biểu thức P =  −  :1−  
với x  0; x  1 Rút gọn biểu
x −1 x x + x − x −1  x 1  +     thức P . Lời giải 2
a) A = 4 + 2 3 + 6 − 2 5 + 5 + 3 ( − = 3 + )2 1 + ( 5 − )2 2( 5 3) 1 + 2 = 3 +1+ 5 −1+ 5 − 3 = 2 5     b) 1 2 x 2 x P =  −  :1−  
x −1 x x + x − x −1  x 1  +        − +  = 1 2 x x 2 x 1  −  :   
x −1 (x +1)( x −1)   x 1  +     ( x − )2 1 ( x x x − + − )2 1 1 2 x +1 1 = : = . = (x +1)( x −1) x +1
(x +1)( x −1) ( x − )2 x −1 1 Câu 2. (1,0 điểm)
Tìm tất cả các giá trị m của để phương trình 2
x − 5x + 3m +1 = 0 ( x là ẩn số; m là tham
số) có hai nghiệm phân biệt x ; x x − x = 15 . 1 2 thỏa mãn 2 2 1 2 Lời giải Có  = 21−12m
Phương trình có hai nghệm phân biệt 7
  0  21−12m  0  m  4 x + x = 5 Theo hệ thức Vi-ét: 1 2
x .x = 3m+1  1 2 Ta có 2 2
x − x = 15  x + x x − x
= 15  x − x = 3 1 2 ( 1 2 )( 1 2 ) 1 2 (x − x )2 = 9 1 2
 (x + x )2 − 4x x = 9 1 2 1 2 2
 5 − 4(3m +1) = 9  21−12m = 9  m = 1(thỏa mãn) Vậy m = 1 Câu 3. (1,5 điểm) Trang 2  x y 5 − = 
a) Giải hệ phương trình y x 6   2 2 x − y = 5
b) Giải phương trình ( x − )4 2
1 = x − 2x + 3 . Lời giải
a) ĐK x  0; y  0 2 2  x y 5  x − y 5 − =   = xy = 6 y x 6    xy 6   2 2   x − y = 5 2 2 2 2 x − y = 5 x − y = 5  6 =  = 6 y xy  x    2 2 x − y = 5 36 2 x − = 5 2  x 36 2 4 2 x −
= 5  x − 5x − 36 = 0  x = 3  2 x x = 3  y = 2 x = 3 −  y = −2
Vậy ngiệm của phương trình S = (  3;2),( 3 − ; 2 − )
b) (x − )4 = x − x +  (x − )4 = (x − )2 +  (x − )4 − (x − )2 2 1 2 3 1 1 2 1 1 − 2 = 0 .
Đặt t = ( x − )2 1 (t  0) Phương trình trở thành 2
t − t − 2 = 0
 t = −1(loại); t = 2 (nhận) x = − 2 +1
Với t = 2  ( x − )2 1 1 = 2   x = 2 +1  2
Vậy ngiệm của phương trình S = − 2 +1; 2 +  1 Câu 4. (1,5 điểm)
a) Tìm tất cả các số nguyên x sao cho giá trị của biểu thức 2
x + x + 6 là một số chính phương.
b) Tìm nghiệm nguyên của phương trình 2 y = − ( 6 3
2 x − x y − 32). Lời giải a) Giải sử 2
x + x + 6 là số chính phương , suy ra tồn tại số k sao cho 2 2
x + x + = k  ( 2 x + x + ) 2 6 4 6 = 4k  ( k )2 2 2
− (2x +1) = 23  (2k + 2x + )
1 (2k − 2x − ) 1 = 23
2k + 2x +1 = 23 TH1:   x = 5
2k − 2x −1 =1 2k + 2x +1 =1 TH2:   x = 6 −
2k − 2x −1 = 23
2k + 2x +1 = 2 − 3 TH3:   x = 6 −
2k − 2x −1 = 1 − Trang 3
2k + 2x +1 = 1 − TH4:   x = 5
2k − 2x −1 = 2 − 3 Với x  6 − ;  5 thì 2
x + x + 6 là số chính phương
b)Tìm nghiệm nguyên của phương trình 2 y = − ( 6 3
2 x − x y − 32). trình 2 y = − ( 6 3
2 x − x y − 32). 2 y = − ( 6 3 x − x y − ) 2 3 6 2
32  y − 2x y + 2x − 64 = 0 6
 ' = −x + 64  0  x  2  x = 1;0;2
Với x = 0  y = 8 Với 2
x = 1  y − 2 y − 62 = 0. (loại) Với 2 x = 1
−  y + 2y − 62 = 0. (loại) Với 2
x = 2  y −16 y + 64 = 0  y = 8 Với 2 x = 2
−  y +16y + 64 = 0  y = 8 − .
Vậy ngiệm nguyên của phương trình là (0;8) ; (0;−8); (2;8); (−2;−8) . Câu 5. (3,0 điểm)
Cho tam giác nhọn ABC ( AB  AC) nội tiếp đường tròn (O) . Kẻ đường cao AH của
tam giác ABC ( H thuộc BC ). Gọi P;Q lần lượt là chân của đường vuông góc kẻ từ H
đến các cạnh AB, AC .
a) Chứng minh PQH = BAH .
b) Hai đường thẳng PQ và BC cắt nhau tại M . Chứng minh M  QH ∽ M  HP và 2 MH = . MB MC .
c) Đường thẳng MA và cắt đường tròn (O) tại K ( K khác A ). KH cắt đường tròn (O)
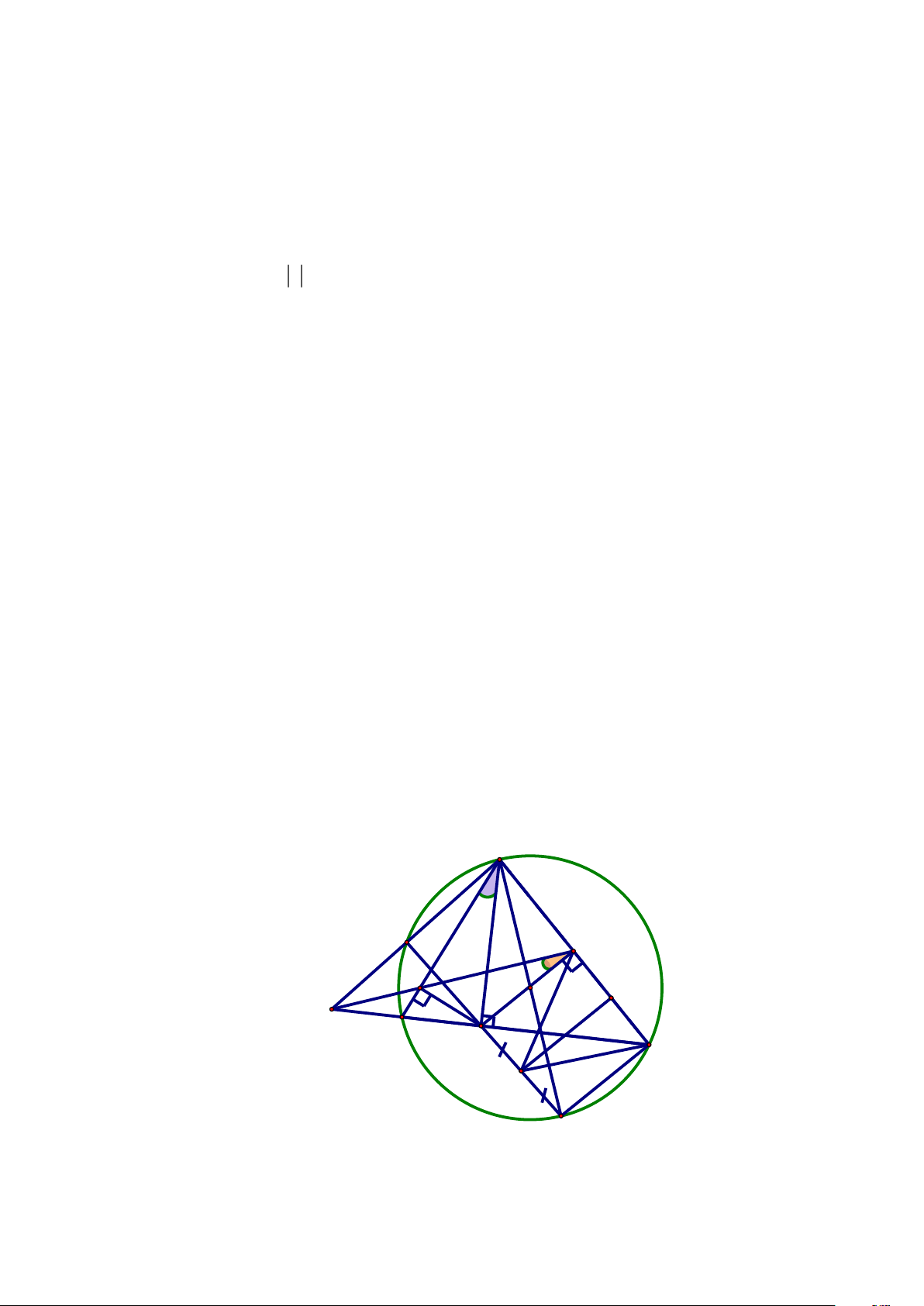
tại D ( D khác K ) . Gọi J là trung điểm của HD . Chứng minh JQ = JC . Lời giải A K Q P O N M B H C J D
a) Tứ giác APHQ có 0 APH + AQH = 180
Suy ra tứ giác APHQ nội tiếp Trang 4  PQH = PAH Hay PQH = BAH .
b) có PQH = BAH (cmt)
mà BAH = MHP ( cùng phụ PBH ) nên MQH = MHP và PMH góc chung MQ MH 2  M  QH ∽ M
 HP(g.g)  =  MH = M . P MQ (1) MH MP
Chứng minh được tứ giác BPQC nội tiếp  MBP = MQC và BMP góc chung MB MP  M  BP ∽ M
 QC(g.g)  =  M . P MQ = M . B MC (2) MQ MC Từ ( ) 1 2
và (2)  MH = M . B MC
c) vì AKBC là tứ giác nội tiếp
nên MKB = MCA (cùng bù với AKB ), mà AMC là góc chung MK MB  M  KB ∽ M  C ( A g.g)  =
 MK.MA = M . B MC MC MA Mà 2 2 MH = M .
B MC  MH = MK.MA
Do AHM vuông tại H  HK là đường cao của AHM (vì MHA∽ MKH )
 AK ⊥ KH  AK ⊥ KD  AD là đường kính của (O) Suy 0
ACD = 90 nên DC ⊥ AC
Mà HQ ⊥ AC  DC // HQ nên HQCD là hình thang
Gọi N là trung điểm QC (3)  JN của là đường trung bình của hình thang HQCD
 JN // HQ  JN ⊥ QC (4)
Từ (3) và (4)  JN là đường trung trực củaQC  JQ = JC Câu 6. (1,0 điểm) 2 x +10
Tìm giá trị nhỏ nhất của biểu thức . 2 x + 9 Lời giải 2 x +10 1 Đặt 2 P = = x + 9 + 2 2 x + 9 x + 9  1 1  8 2 2 =  x + 9 +  + x + 9 2 9  x + 9 9  1 8 10  p  2. + .3 = 3 9 3 10
Vậy giá trị nhỏ nhất của p = khi x = 0 3
---------------------------------@Hết@--------------------------------- Trang 5