Đề Thi Tuyển Sinh 10 Toán Chuyên Tin Hùng Vương Phú Thọ 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 PHÚ THỌ
TRUNG HỌC PHỔ THÔNG CHUYÊN HÙNG VƯƠNG Môn: Toán ĐỀ CHÍNH THỨC
(Dành cho thí sinh thi chuyên Tin)
Thời gian làm bài: 150 phút, không kể thời gian phát đề Đề thi có 01 trang
Câu 1 (2,0 điểm).
a) Tìm tất cả các giá trị của tham số m để phương trình 2 x − (m − ) 2 2
1 x + m − m = 0 có hai
nghiệm phân biệt x , x thỏa mãn 2 x + x = x − x . 1 2 1 2 1 2 1 2 3 2 2 x y
b) Cho x, y là các số thực thỏa mãn − =
. Tính giá trị của biểu thức P = + . y x 2x + y 2 2 y x Câu 2 (2,0 điểm).
a) Tìm tất cả các cặp số nguyên dương ( ; x y) thỏa mãn ( 2 x − x − )( 2
1 y + xy − 9) = 2x +1.
b) Cho n là số nguyên dương lẻ sao cho 3n 7n +
chia hết cho 11. Tìm số dư khi chia
2n 6n 2023n + + cho 11.
Câu 3 (2,0 điểm).
2 x −3y =16 −3x +9y
a) Giải hệ phương trình  ( x, y  ).
2 x − 3 + y + 3 = 5y +1  1 1 1 1
b) Viết lên trên bảng 2023 số: 1; ; ; ; ;
. Mỗi bước ta xoá đi 2 số x, y bất kì trên 2 3 2022 2023 xy
bảng rồi viết lên bảng số
(các số còn lại trên bảng giữ nguyên). Thực hiện liên tục thao tác x + y +1
trên cho đến khi trên bảng chỉ còn lại đúng một số. Hỏi số đó bằng bao nhiêu?
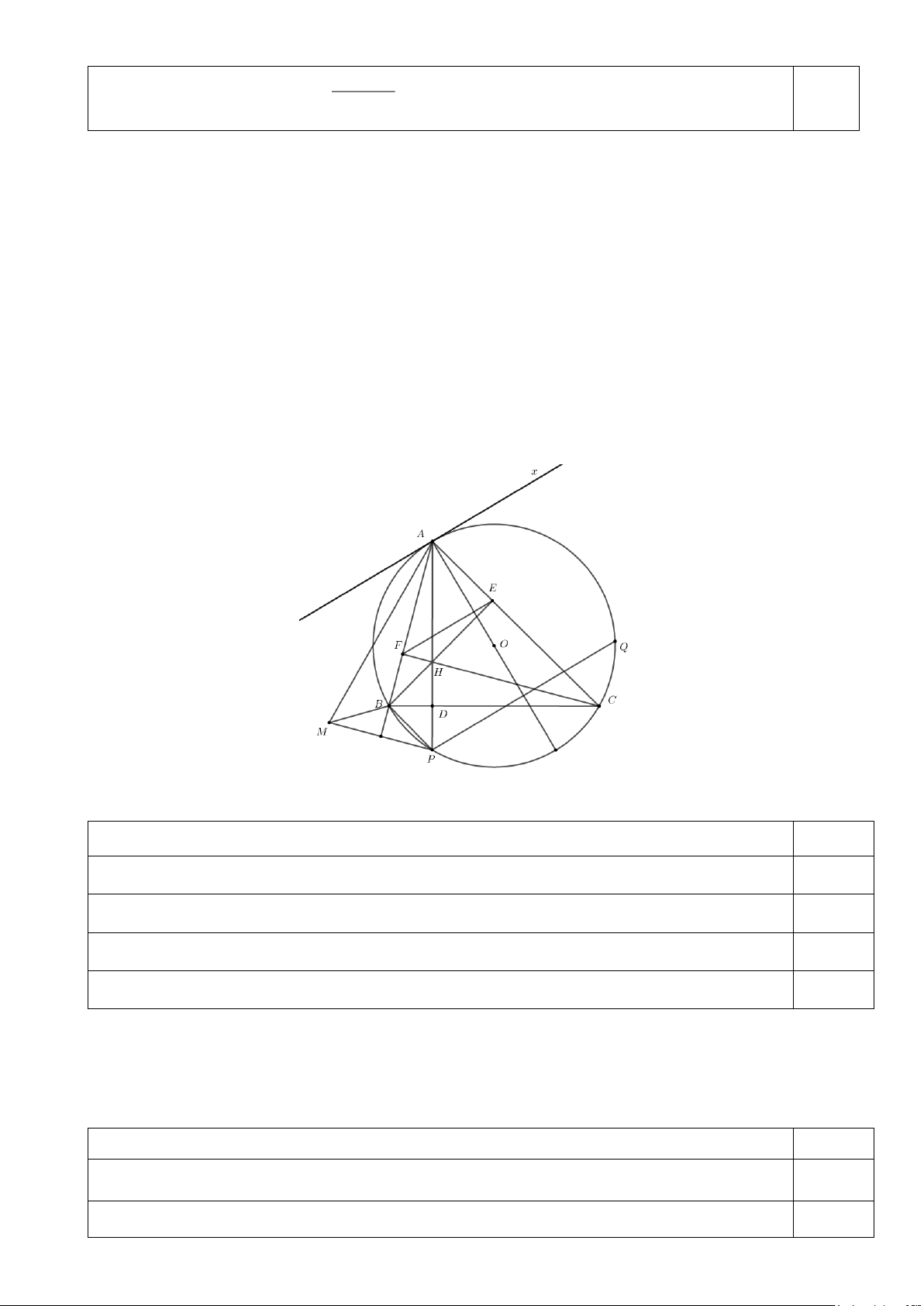
Câu 4 (3,0 điểm). Cho tam giác nhọn ABC với AB  AC nội tiếp đường tròn (O; R), các đường cao
AD, BE,CF cắt nhau tại H. Gọi P là giao điểm thứ hai của AD và (O), M là điểm đối xứng với P qua . AB
a) Chứng minh tứ giác AHBM nội tiếp.
b) Qua P kẻ đường thẳng song song với EF cắt (O) tại Q . Chứng minh Q đối xứng với P qua . OA
c) Gọi K là trung điểm của EF . Chứng minh đường thẳng AK và các tiếp tuyến của (O) tại
B,C đồng quy.
Câu 5 (1,0 điểm). Xét ba số x, y, z  2 thỏa mãn 4xyz = 9( x + y + z) + 27; tìm giá trị lớn nhất 2 2 2 x − 4 y − 4 z − 4 của biểu thức Q = + + . x y z
.......................Hết.....................
Họ và tên thí sinh:………………………………………………Số báo danh:...........................
Cán bộ coi thi không giải thích gì thêm. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 PHÚ THỌ
TRUNG HỌC PHỔ THÔNG CHUYÊN HÙNG VƯƠNG
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC MÔN TOÁN
(Dành cho thí sinh thi chuyên Tin)
Hướng dẫn chấm có 06 trang
I. Một số chú ý khi chấm bài
- Đáp án chấm thi dưới đây dựa vào lời giải sơ lược của một cách. Khi chấm thi giám khảo cần bám
sát yêu cầu trình bày lời giải đầy đủ, chi tiết, hợp logic và có thể chia nhỏ đến 0,25 điểm.
- Thí sinh làm bài theo cách khác với hướng dẫn chấm mà đúng thì tổ chấm cần thống nhất cho
điểm tương ứng với thang điểm của hướng dẫn chấm.
- Điểm bài thi là tổng điểm các câu không làm tròn số.
II. Đáp án – Thang điểm Câu 1 (2,0 điểm).
a) Tìm tất cả các giá trị của tham số m để phương trình 2 x − (m − ) 2 2
1 x + m − m = 0 có hai
nghiệm phân biệt x , x thỏa mãn 2 x + x = x − x . 1 2 1 2 1 2 Đáp án Điểm
Phương trình có hai nghiệm phân biệt x và x   = 1− m  0  m  1. 1 2 0,25
Xét 2 x + x = x − x  4( x + x = x − x
 3(x + x + 4x x = 0. 0,25 1 2 )2 1 2 )2 ( 1 2)2 1 2 1 2 1 2
x + x = 2 m −1  1 2 ( )
Áp dụng định lý Vi–ét, ta có:  2
x x = m − m  1 2 0,25 Ta được (m − )2 + ( 2 12 1 4 m − m) = 0 2
 4m − 7m + 3 = 0. m = 1   3 3 
. Kết hợp với điều kiện, giá trị m = thỏa mãn. 0,25 m = 4  4 1 2 3 2 2 x y
b) Cho x, y là các số thực thỏa mãn − =
. Tính giá trị của biểu thức P = + . y x 2x + y 2 2 y x Đáp án Điểm 1 2 3 Ta có: − =
 (x − 2y)(2x + y) 2 2
= 3xy  2x − 6xy − 2y = 0. 0,25 y x 2x + y x 3 + 13 −  = x 3 13 hoặc = . 0,25 y 2 y 2 2 x 3 + 13 y 2 3 − + 13 2 2 x y  x y  0,25 Với =  = = . Ta được P = + = + − 2 =11.   y 2 x 3 + 13 2 2 2 y x  y x  2 x 3 − 13 y 2 3 − − 13 2 2 x y  x y  0,25 Với =  = = . Ta được P = + = + − 2 =11.   y 2 x 3 − 13 2 2 2 y x  y x 
Câu 2 (2,0 điểm).
a) Tìm tất cả các cặp số nguyên dương ( ; x y) thỏa mãn ( 2 x − x − )( 2
1 y + xy − 9) = 2x +1. Trang 2 Đáp án Điểm Vì ( 2 x − x − )( 2
1 y + xy − 6) = 2x +1 nên ( x + ) ( 2 2 1 x − x − ) 1 0,25
 ( x + )( x − ) ( 2 2 1 2 3 x − x − ) 1 0,25  ( 2
x − x − ) ( 2 4 4 3 x − x − ) 1   ( 2
x − x − ) +  ( 2 4 1 1 x − x −   )1  ( 2 1 x − x + ) 1 0,25  ( 2 x − x − ) 1 −  1;1
 x  0;1;−1; 
2 , mà x nguyên dương  x 1;  2 .
Với x = 1 , ta có phương trình: 2
y + y − 9 = −3  y = 2 hoặc y = 3
−  0 (không thỏa mãn)
Với x = 2 , ta có phương trình: 2 2
y + 2 y − 9 = 5  y + 2 y −14 = 0 (loại do phương trình có 2 nghiệm không nguyên). 0,25 Thử lại ( ;
x y) = (1;2) thỏa mãn phương trình đã cho.
Vậy cặp số nguyên dương ( ;
x y) cần tìm là (1;2) .
b) Cho n là số nguyên dương lẻ sao cho 3n 7n +
chia hết cho 11. Tìm số dư khi chia
2n 6n 2023n + + cho 11. Đáp án Điểm - Với 1 3n 7n n =  +
= 3 + 7 =10 11 (không thỏa mãn). - Với n n 3 3
n = 3  3 + 7 = 3 + 7 = 370 11 (không thỏa mãn). 0,25 - Với n n 5 5
n = 5  3 + 7 = 3 + 7 = 17050 11 (thỏa mãn).
Suy ra n  5 . Giả sử n = 5k + r (0  r  4) . k k Ta có 5 + 5 + + = ( 5) + ( 5 3 7 3 .3 7 ) .7  3 + 7 .(− ) 1 k k r k r r r r r
11 với r = 0,1, 2,3, 4 . - Khi r = 0 3 7 .( ) 1 k 1 ( ) 1 k r r  + − = + −
11 xảy ra khi k lẻ. - Khi r = 1 3 7 .( ) 1 k 3 7.( ) 1 k r r  + − = + − 11 với mọi k . 0,5 - Khi r = 2 ( )k 2 2 3 7 . 1 3 7 .( ) 1 k r r  + − = + − 11 với mọi k . - Khi r = 3 ( )k 3 3 3 7 . 1 3 7 .( ) 1 k r r  + − = + − 11 với mọi k . - Khi r = 4 ( )k 4 4 3 7 . 1 3 7 .( ) 1 k r r  + − = + − 11 với mọi k .
Vậy n = 5k ( k lẻ). k k Khi đó ( ) ( ) ( )5 5 5 2 6 2023 2 6 2023 k ( ) 1 k ( ) 1 k ( ) 1 k n n n + + = + +  − + − + − (mod1 ) 1 0,25  3
− (mod11) . Vậy 2n 6n 2023n + + chia 11 có số dư là 8. Câu 3 (2,0 điểm).
2 x −3y =16 −3x +9y
a) Giải hệ phương trình  ( x, y  ).
2 x − 3 + y + 3 = 5y +1  Trang 3 Đáp án Điểm
Điều kiện: x − 3y  0; x  3; y  3. − Ta có: 0,25
(1)  3(x − 3y) + 2 x − 3y −16 = 0  ( x −3y − 2)(3 x −3y +8) = 0  x −3y = 2  x = 4 + 3 . y
Thế x = 3y + 4 vào phương trình (2) ta được
2 3y +1 + y + 3 = 5y +1  2( 3y +1 − 2) + ( y +3 − 2) = 5y +1−6 0,25 3( y − ) 1 y −1  + − (  
y − ) =  ( y − ) 6 1 2 5 1 0 1  + − 5 = 0 (*) 3y 1 2 y 3 2  3y 1 2 y 3 2  + + + + + + + +   6 1 1 Nhận thấy +
− 5  3+ − 5  0 với mọi y  −3. 3y +1 + 2 y + 3 + 2 2 0,25
Do đó (*) có nghiệm duy nhất y = 1(thỏa mãn).
Với y = 1 ta được x = 7 (thỏa mãn). 0,25
Vậy hệ phương trình có nghiệm ( ; x y) = (7; ) 1 . 1 1 1 1
b) Viết lên trên bảng 2023 số: 1; ; ; ; ;
. Mỗi bước ta xoá đi 2 số x, y bất kì trên 2 3 2022 2023 xy
bảng rồi viết lên bảng số
(các số còn lại trên bảng giữ nguyên). Thực hiện liên tục thao tác x + y +1
trên cho đến khi trên bảng chỉ còn lại đúng một số. Hỏi số đó bằng bao nhiêu? Đáp án Điểm xy 1 1 1 1 1  1  1  Đặt z =  = + +  +1 = +1 +1    ( ) 1 . x + y +1 z x y xy z  x  y  0,25
Với mỗi tập các số dương x ; x ;...x tùy ý, xét biểu thức: 1 2 n      P( 1 1 1
x ; x ;...x =  +1 +1.... +1. 0,25 1 2 n ) x x x  1  2   n  xy Từ ( )
1 suy ra mỗi lần xóa đi 2 số bất kì x, y rồi viết lên bảng số các số còn lại trên x + y +1
bảng giữ nguyên thì giá trị biểu thức P của các số trên bảng không đổi. 0,25 1 1 1 1 1 
Gọi số cuối cùng là a  P(a) = P ; ; ;...; ;   1 2 3 2022 2023        1 1   1   1   1  1 0,25  +1 = +1 .    +1... +1. +1 = 2024! a = . a 1 1 1 1  2024!−1        2   2022   2023  Trang 4 1
Vậy số còn lại trên bảng là a = . 2024!−1
Câu 4 (3,0 điểm). Cho tam giác nhọn ABC với AB  AC nội tiếp đường tròn (O; R), các đường cao
AD, BE,CF cắt nhau tại H. Gọi P là giao điểm thứ hai của AD và (O), M là điểm đối xứng với P qua . AB
a) Chứng minh tứ giác AHBM nội tiếp.
b) Qua P kẻ đường thẳng song song với EF cắt (O) tại Q . Chứng minh Q đối xứng với P qua . OA
c) Gọi K là trung điểm của EF . Chứng minh đường thẳng AK và các tiếp tuyến của (O) tại
B,C đồng quy.
a) Chứng minh tứ giác AHBM nội tiếp. Đáp án Điểm
a) Vì M là điểm đối xứng với P qua AB nên AMB = APB 0,25
Mà APB = ACB (góc nội tiếp cùng chắn cung AB ). 0,25
Mặt khác: ACB = AHE (vì tứ giác AEHF nội tiếp) 0,25
Ta được AMB = AHE do đó tứ giác AHBM nội tiếp. 0,25
(Lưu ý: Học sinh không giải thích rõ lý do để các góc bằng nhau vẫn cho điểm tối đa).
b) Qua P kẻ đường thẳng song song với EF cắt (O) tại Q . Chứng minh Q đối xứng với P qua . OA Đáp án Điểm
b) Kẻ tiếp tuyến Ax của đường tròn (O) . Ta có xAC = ABC 0,25
ABC = AEF (vì tứ giác BCEF nội tiếp) 0,25 Trang 5  xAC = AEF
 Ax, EF song song. Mà OA ⊥ Ax  OA ⊥ EF 0,25
Theo giả thiết PQ, EF song song với nhau nên PQ ⊥ O .
A Do đó theo định lý đường kính, 0,25
dây cung ta được Q đối xứng với P qua OA .
(Lưu ý: Học sinh không giải thích rõ lý do để các góc bằng nhau vẫn cho điểm tối đa).
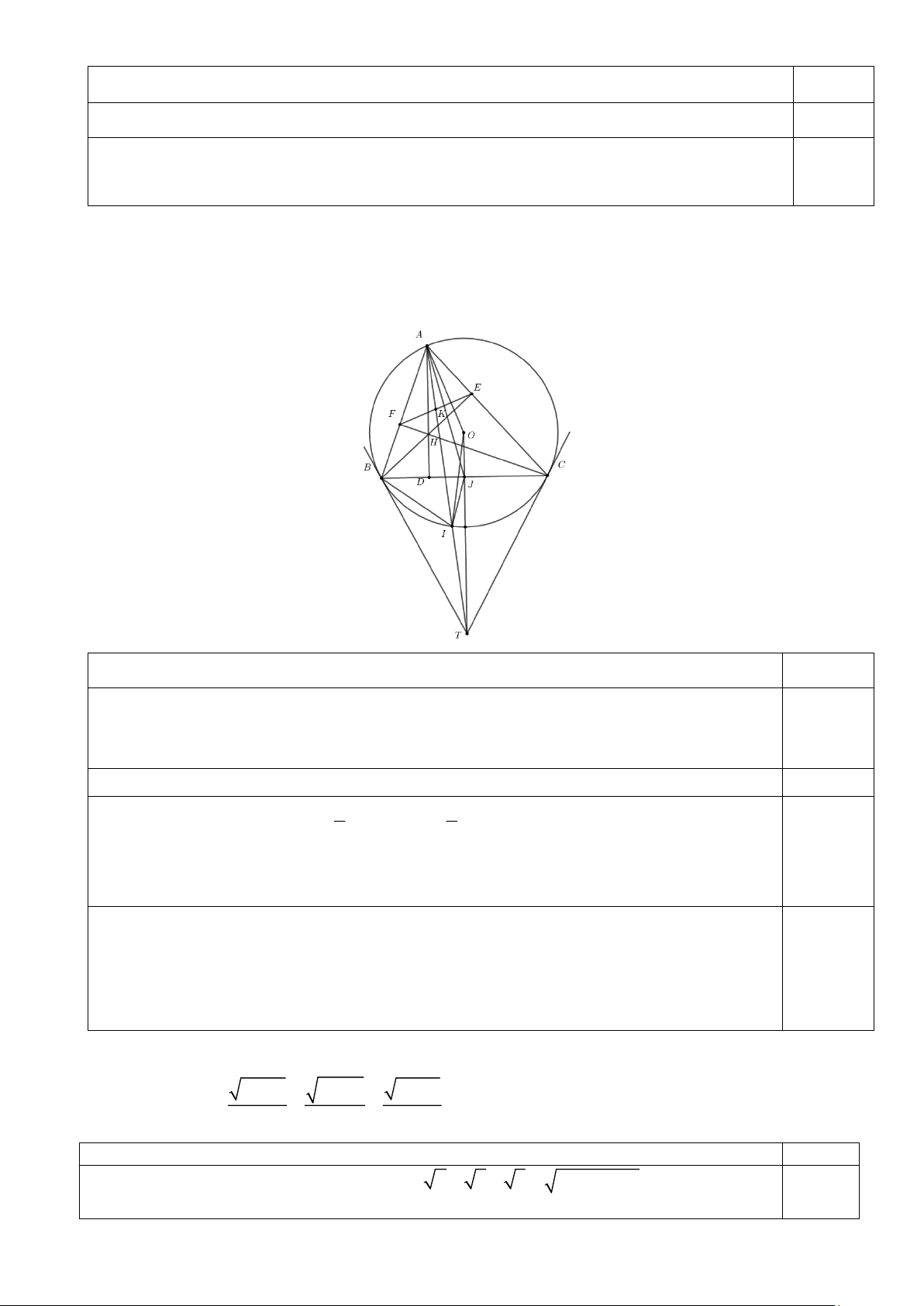
c) Gọi K là trung điểm của EF . Chứng minh đường thẳng AK và các tiếp tuyến của (O) tại
B,C đồng quy. Đáp án Điểm
Tiếp tuyến tại B,C cắt nhau ở T . Gọi I = AT  (O) . Lấy J là trung điểm của BC
 O, J ,T thẳng hàng. 0,25 Có 2
TI.TA = TB = TJ.TO  tứ giác AOJI nội tiếp.
 IJT = OAI = OIA = OJA  AJB = BJI  JB là phân giác của góc AJI 0,25 1 1
Xét AJC = 180 − AJB = 180 − AJI = 180 − AOI = 180 − ACI = ABI 2 2
Xét AJC và ABI có: AJC = ABI ; ACJ = AI . B 0,25
 JAC = BAI ( ) 1
Mặt khác AEF và ABC đồng dạng có hai đường trung tuyến tương ứng là AK , AJ
 KAF = JAC (2) 0,25
Từ (1),(2)  BAI = FAK  I  AK  ,
A I , K thẳng hàng. Vậy đường thẳng AK và hai
tiếp tuyến của (O) tại B và C đồng quy.
Câu 5 (1,0 điểm). Xét ba số x, y, z  2 thỏa mãn 4xyz = 9( x + y + z) + 27; tìm giá trị lớn nhất 2 2 2 x − 4 y − 4 z − 4 của biểu thức Q = + + . x y z Đáp án Điểm
Sử dụng bất đẳng thức: Với a, ,
b c  0, ta có a + b + c  3(a + b + c). 0,25
Áp dụng bất đẳng thức trên ta có: Trang 6 4 4 4   1 1 1   1 1 1  Q = 1− + 1− + 1−  33− 4 + +   = 9 −12 + + 2 2 2 2 2 2  2 2 2  x y z   x y z   x y z  2 1 1 1 1  1 1 1  Lại có + +  + + . 2 2 2   x y z 3  x y z  2  1 1 1  Suy ra Q  9 − 4 + + .    x y z   1 1 1  27
Từ giả thiết 4xyz = 9(x + y + z) + 27  9 + + + = 4 (*)  
 xy yz zx  xyz 2 3 1 1 1 1  1 1 1  1 1  1 1 1  Với + +  . + +   và  . + +   0,25 xy yz zx 3  x y z  xyz 27  x y z  2 3  1 1 1   1 1 1  Từ (*) ta có 3 + + + + +  4     (* ) *  x y z   x y z  1 1 1 Đặt t = + +  0 . x y z 0,25
Khi đó (**)  t + t −   (t − )(t + )2 3 2 3 4 0 1
2  0  t  1 (do (t + )2 2  0 ). 2  1 1 1  Suy ra 2 Q  9 − 4 + +  9 − 4.1 = 5.    x y z  0,25
Dấu “=” xảy ra khi và chỉ khi x = y = z = 3.
Vậy giá trị lớn nhất của Q là 5.
.......................Hết..................... Trang 7