Đề Thi Tuyển Sinh 10 Toán Không Chuyên Sở GD Gia Lai 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TỈNH GIA LAI
TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG
Môn: TOÁN (không chuyên) ĐỀ CHÍNH THỨC
Thời gian: 120 phút (không kể thời gian phát đề)
(Đề thi gồm có 01 trang)
Họ và tên thí sinh:................................................................... Số báo danh: ................................
Câu 1 (2,0 điểm). 4x + 5y = 23
a) Không sử dụng máy tính cầm tay, giải hệ phương trình:  . x  − 3y = −7
b) Gọi x , x là hai nghiệm phân biệt của phương trình : 2
x − 3x − 2 = 0. 1 2 x − 3 x − 3
Tính giá trị của biểu thức 1 2 M = + . x x 2 1
Câu 2 (2,0 điểm).
a) Xác định hàm số y = ax + b, biết đồ thị hàm số là đường thẳng song song với đường
thẳng d :y = 2x và đi qua điểm ( A 1;4) . b) Cho parabol 2 ( )
P : y = x và đường thẳng 2
d : y = 4x + m + 5m ( m là tham số). Tìm m để
đường thẳng d tiếp xúc với parabol ( ) P .
Câu 3 (2,0 điểm).  x 7 x 12 1   x 3 − + +
Cho biểu thức A =  + . , 
với x  0, x  1, x  9 . x 4 x 3
x 1  x 3  − + − −    
a) Rút gọn biểu thức A.
b) Tìm tất cả các giá trị x nguyên để biểu thức A nhận giá trị nguyên.
Câu 4 (2,0 điểm).
a) Tìm độ dài cạnh hình vuông biết rằng nếu tăng độ dài cạnh hình vuông thêm 2 đơn vị thì
diện tích của nó sẽ tăng lên gấp 4 lần so với diện tích ban đầu ? b) Giải phương trình: 2
x + 3 = −x − 5x − 5 .
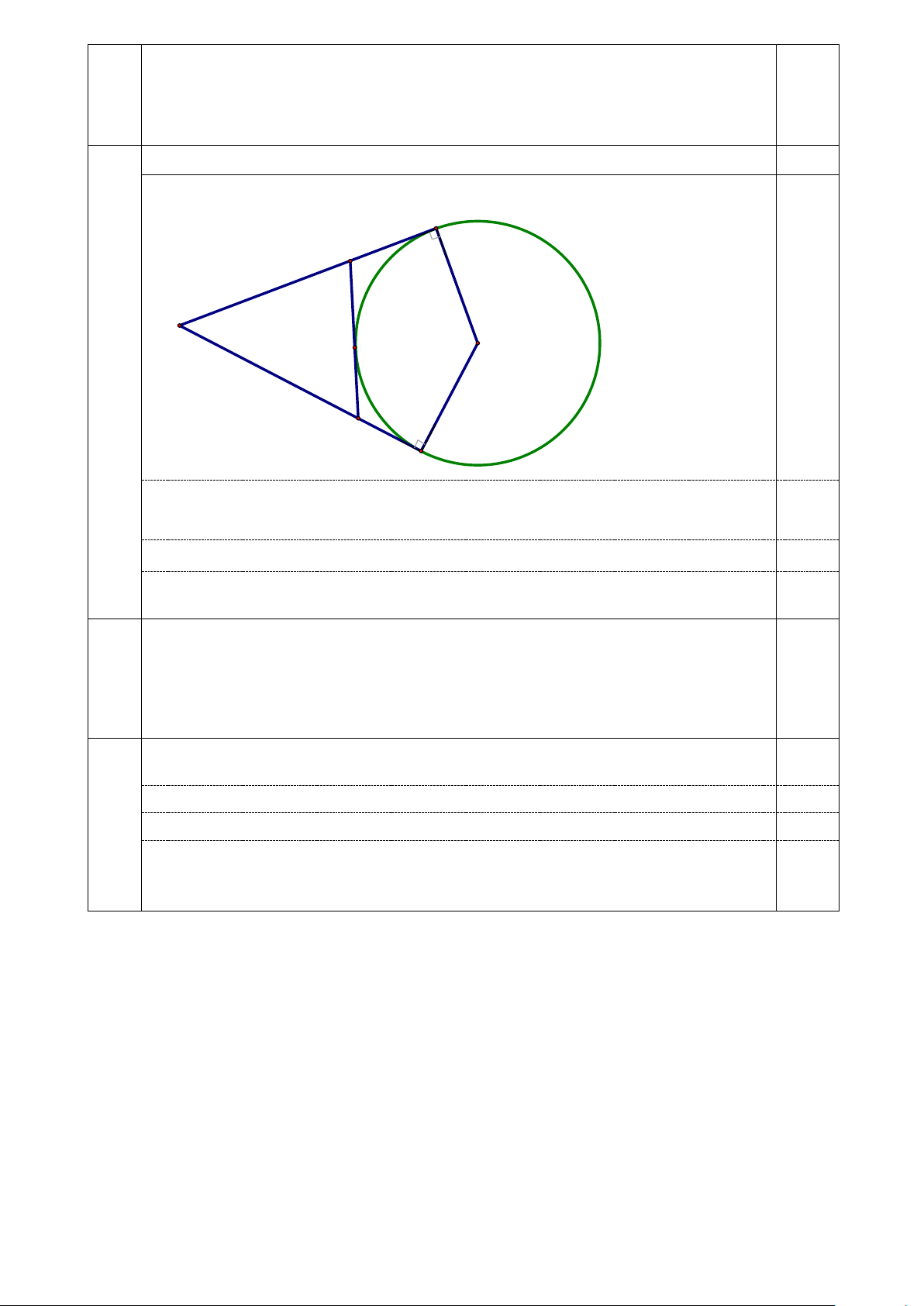
Câu 5 (2,0 điểm). Cho đường tròn ( )
O và điểm Anằm bên ngoài đường tròn. Kẻ các tiếp tuyến A , B AC với đường tròn ( ) O ( ,
B C là các tiếp điểm ) .
a) Chứng minh bốn điểm , A , B ,
O C cùng thuộc một đường tròn.
b) Trên cung nhỏ BC của đường tròn ( )
O lấy điểm M bất kỳ( M không trùng với , B C ) .
Tiếp tuyến tại M của đường tròn ( ) O cắt A ,
B AC theo thứ tự tại D,E . Chứng minh tam giác
ADE có chu vi không đổi khi M chuyển động trên cung nhỏ BC .
--------------------HẾT---------------------- Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TỈNH GIA LAI
TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG, (Gồm có 04 trang)
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
MÔN TOÁN (không chuyên) A. Hướng dẫn chấm
- Thí sinh làm bài theo cách riêng của mình mà vẫn đáp ứng các yêu cầu của đáp án thì giám
khảo cân nhắc mức độ bài làm, đối chiếu với yêu cầu đề thi và đáp án để cho điểm một cách hợp lý.
- Việc chi tiết hóa điểm số (nếu có) tuyệt đối không làm thay đổi thang điểm của từng câu và
toàn bài. Có thể chia nhỏ điểm thành phần nhưng không được nhỏ hơn 0,1 điểm.
- Điểm toàn bài sau khi chấm xong không làm tròn.
- Học sinh có các cách diễn đạt khác nhau nhưng thể hiện đúng nội dung thì vẫn cho điểm tối đa.
B. Đáp án và thang điểm Câu Đáp án Điểm 4x + 5y = 23
Giải hệ phương trình sau :  x  − 3y = −7 4x + 5y = 23 4x + 5y = 23 Ta có :    0,25
x − 3y = −7
4x −12y = −28 x − 3y = 7 − 1a   0,25 1  7y = 51 x = 3y − 7   0,25 y  = 3 x = 2  
Vậy : x = 2,y = 3 là nghiệm của hệ phương trình. 0,25 y = 3
Gọi x và x là hai nghiệm của phương trình: 2
x − 3x − 2 = 0. 1 2 x − 3 x − 3
Tính giá trị của biểu thức 1 2 M = + . x x 2 1 x + x = 3
Theo hệ thức Vi –ét ta có 1 2  0,25 x x = −2 1b  1 2 2 2 x − 3 x − 3
x + x − 3 x + x 1 2 ( 1 2 1 2 ) M = + = 0,25 x x x x 2 1 1 2
(x + x )2 −2x x −3 x + x 1 2 1 2 ( 1 2) = 0,25 x x 1 2 Trang 2 ( )2 3 − 2( 2 − ) − 3.3 9+ 4− 9 = = = −2 0,25 2 − 2 −
Xác định hàm số y = ax + b, biết đồ thị hàm số là đường thẳng song song
với đường thẳng d :y = 2x và đi qua điểm A(1;4).
Vì đồ thị hàm số song song với đường thẳng d :y = 2x nên a = 2, b  0 0,25
2a Mặt khác, đồ thị hàm số đi qua điểm A(1;4) nên ta có 4=2.1+b 0,25
 b = 2 ( thỏa mãn ). 0,25
Vậy y = 2x + 2 0,25 Cho parabol 2 ( )
P : y = x và đường thẳng 2
d : y = 4x + m + 5m ( m là tham
số). Tìm m để đường thẳng d tiếp xúc với parabol ( ) P .
Phương trình hoành độ giao điểm của d và ( ) P : 0,25 2 2 2 2
x = 4x + m + 5m  x − 4x − m − 5m = 0 (*) 2 2b   = (− ) − ( 2 −m − ) 2 2 1
5m = m + 5m+ 4 0,25
Đường thẳng d tiếp xúc với ( )
P khi và chỉ khi phương trình (*) có nghiệm m = 1 − 0,25 kép 2
  = 0  m + 5m+ 4 = 0   m = 4 −
Vậy m = −1; m = −4 thì đường thẳng d tiếp xúc với parabol ( ) P . 0,25  x 7 x 12 1   x 3 − + +
Rút gọn biểu thức A =  + . ,  x 4 x 3
x 1  x 3  − + − −    
với x  0, x  1, x  9 .   ( x 4)( x )3  − − 1   x 3 + A = 0,25  ( +     x − ) 1 ( x − ) . 3 x 1   x 3 − −     3a  x 4 1   x 3 − + =  + .   0,25 x 1
x 1  x 3  − − −    
 x 3  x 3 − + =  .   0,25
x 1   x 3 − −     x + 3 = 0,25 x −1
Tìm tất cả các giá trị x nguyên để biểu thức A nhận giá trị nguyên. x + 3 4 Ta có: A = = 1+ 0,25 3b x −1 x −1 4 A nguyên khi
Z tức là x −1 là ước của 4 0,25 x −1 Trang 3  x 1 1  − = − x = 0    x −1= 1  x = 2 x = 0     x −1= 2  x = 3 x = 4 Suy ra      0,25 x −1= 2 − x = 1 − (VN) x = 9(l)      − = − = − x = 25 x 1 4 x 3(VN)    x −1= 4  x = 5
Vậy có ba giá trị nguyên của x là: x = 0, x = 4, x = 25. 0,25
Tìm cạnh hình vuông biết rằng nếu tăng độ dài cạnh hình vuông thêm 2 đơn
vị thì diện tích của nó sẽ tăng lên gấp 4 lần so với diện tích ban đầu ?
Gọi x (x  0) là độ dài cạnh của hình vuông cần tìm. 0,25
Diện tích hình vuông là : 2 S = x 1
Khi tăng độ dài hình vuông thêm 2 đơn vị, độ dài cạnh hình vuông là : x + 2 0,25
và diện tích hình vuông là : 2 S = (x + 2) 4a 2
Theo giả thiết bài toán ta có : S = 4S nên x + 2 = 2 ( 2) 4x 2 1 0,25 x = 2 (N) 2 3x 4x 4 0   − − =  2  x = − (L) 0,25  3
Vậy hình vuông cần tìm có cạnh bằng 2 (đơn vị độ dài). Giải phương trình sau: 2
x + 3 = −x − 5x − 5
Điều kiện: x + 3  0  x  −3
Với điều kiện trên phương trình đã cho tương đương với phương trình 0,25 2
x + 3 −1= −x − 5x − 6 x + 2 
= −(x + 2)(x + ) 3 x + 3 +1 4b 0,25 (    x + ) 1 2  + x + 3 = 0  x + 3 +1  x + 2 = 0   1  0,25 + x + 3 = 0 (*)  x + 3 +1
Với x  −3 phương trình (* ) vô nghiệm nên phương trình đã cho có 0,25
nghiệm duy nhất x = −2 .
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn. Kẻ các tiếp
tuyến AB, AC với đường tròn (O) (B, C là các tiếp điểm). 5
a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.
b) Trên cung nhỏ BC của đường tròn (O) lấy điểm M bất kỳ (M khác B, Trang 4
C). Tiếp tuyến tại M của đường tròn (O) cắt AB, AC theo thứ tự tại D, E.
Chứng minh tam giác ADE có chu vi không đổi khi M chuyển động trên cung nhỏ BC.
a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn. B D A 0,25 M O 5a E C
Vì AB, AC là các tiếp tuyến của đường tròn (O) nên : 0,25 0 0
ABO = 90 ; ACO = 90 Tứ giác ABOC có 0
ABO + ACO = 180 . 0,25
Suy tứ giác ABOC nội tiếp. Vậy bốn điểm A, B, O, C cùng thuộc một đường 0,25 tròn.
b) Trên cung nhỏ BC của đường tròn (O) lấy điểm M bất kỳ (M khác B,
C). Tiếp tuyến tại M của đường tròn (O) cắt AB, AC theo thứ tự tại D, E.
Chứng minh tam giác ADE có chu vi không đổi khi M chuyển động trên cung nhỏ BC.
Xét (O) : DB, DM là hai tiếp tuyến cắt nhau tại D nên DB = DM 0,25 Tương tự: EC = EM
Chu vi tam giác ADE: AD + AE + DE = AD + AE + DM + EM 0,25
5b = AD + AE + DB + EC = AB + AC 0,25
Vì đường tròn (O), điểm A không thay đổi nên AB + AC không thay đổi.
Vậy tam giác ADE có chu vi không đổi khi M chuyển động trên cung nhỏ 0,25 BC. Trang 5