Đề Thi Tuyển Sinh 10 Toán Không Chuyên Sở GD Quảng Ngãi 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT QUẢNG NGÃI Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
Bài 1. (2,0 điểm)
1. Thực hiện phép tính 3 49 − 121 . 1
2. Vẽ đồ thị (P) của hàm số 2 y = x . 2
3. Cho hai đường thẳng (d) : y = 2x +1 và (d )
 : y = ax + b (a  0) . Tìm a, b biết (d )
song song với (d ) và đi qua điểm ( A 2;3) .
Bài 2. (2,0 điểm)
1. Giải phương trình và hệ phương trình sau: 2x − y = 3 a) 4 2
x − 3x − 4 = 0. b)  . 3  x + 2y =1
2. Cho phương trình 2 x − (m − ) 2 2
1 x + m − 4 = 0 , với m là tham số.
a) Tìm m để phương trình có hai nghiệm phân biệt.
b) Khi phương trình có hai nghiệm x , x , tìm tất cả các giá trị của m để biểu thức 1 2 2 2 2
P = x + x + x x + m đạt giá trị nhỏ nhất. 1 2 1 2
Bài 3. (1,5 điểm)
Hai đội công nhân cùng thi công một đoạn đường nông thôn và dự định hoàn
thành công việc đó trong 16 ngày. Khi làm được 12 ngày thì đội I được điều động đi
làm việc ở nơi khác. Những ngày sau đó, đội II làm việc với năng suất gấp 1,5 lần
năng suất ban đầu nên đã hoàn thành công việc đúng thời gian dự định. Hỏi theo năng
suất ban đầu, nếu mỗi đội làm một mình thì phải bao nhiêu ngày mới hoàn thành công việc trên? Bài 4. (3,5 điểm)
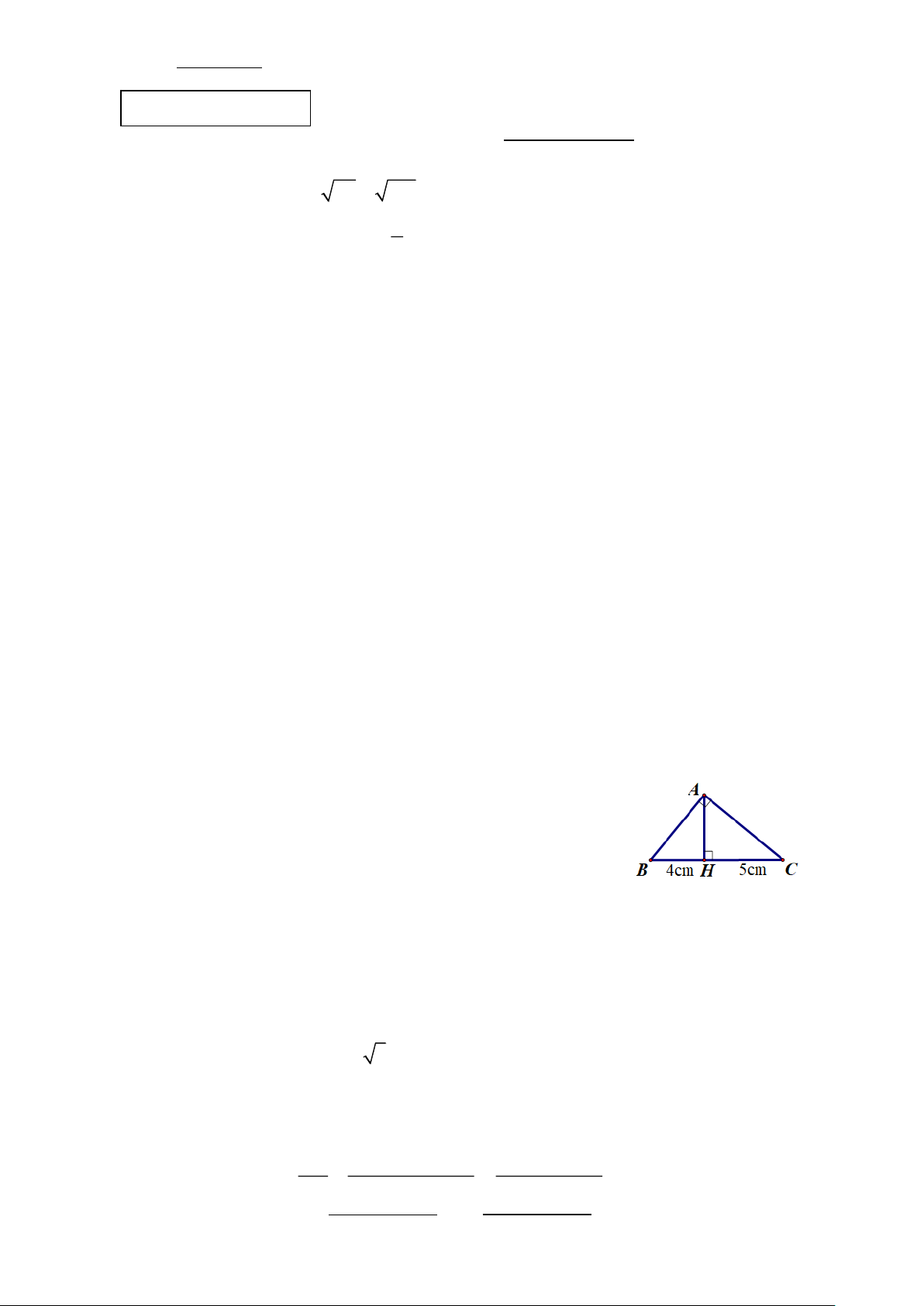
1. Cho tam giác ABC vuông tại A , đường cao AH .
Biết BH = 4 cm , HC = 5cm (như hình vẽ). Tính
độ dài AB và AH.
2. Cho tam giác ABC có ba góc nhọn ( AB  AC ) nội tiếp đường tròn (O; R) . Hai
đường cao AE và BF cắt nhau tại H .
a) Chứng minh tứ giác CEHF nội tiếp đường tròn. Xác định tâm của đường tròn đó.
b) Kẻ đường kính AD của đường tròn (O) . Chứng minh tứ giác BHCD là hình
bình hành. Biết BC = R 3 , tính AH theo R.
c) Gọi N là giao điểm của đường thẳng CH và AB , K là giao điểm của hai
đường thẳng BC và FN . Chứng minh BK CE = BE CK .
Bài 5. (1,0 điểm) 1 1 1 Giải phương trình + = . 2 2 2 3x x −12x + 2024 x − 3x + 506 HẾT
Ghi chú: Giám thị không giải thích gì thêm. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT QUẢNG NGÃI Môn thi: TOÁN
Thời gian làm bài: 120 phút ĐỀ CHÍNH THỨC HƯỚNG DẪN CHẤM
Bài 1. (2,0 điểm)
1. Thực hiện phép tính 3 49 − 121 . 1
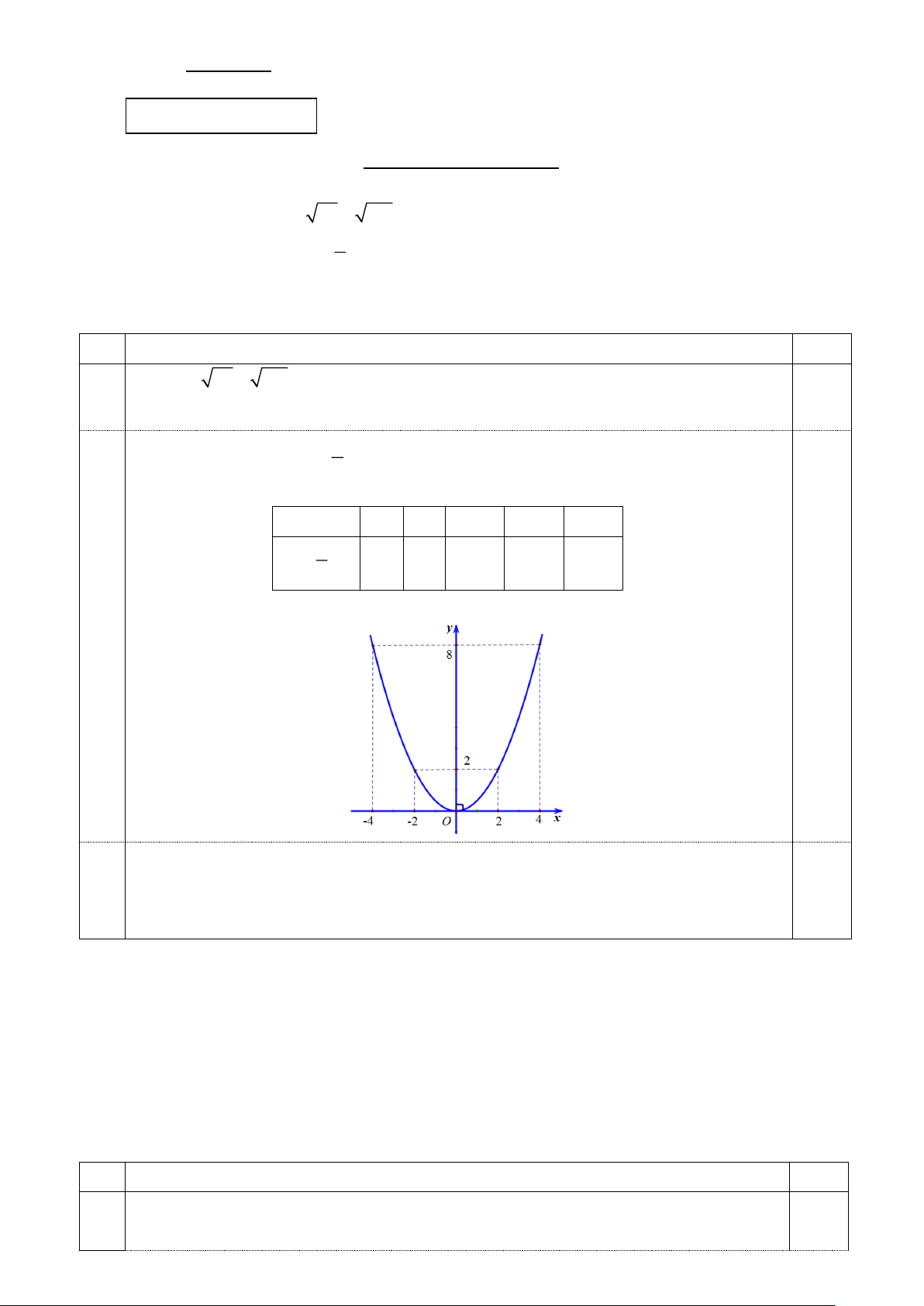
2. Vẽ đồ thị của hàm số 2 y = x . 2
3. Cho hai đường thẳng (d ) : y = 2x +1 và (d )
 : y = ax + b (a  0) . Tìm a,b biết (d ) song
song (d) và đi qua điểm ( A 2;3) . Bài
Tóm tắt cách giải Điểm
Ta có 3 49 − 121 = 3.7 −11 0.5 1.1 = 21−11=10 0.5 1
Vẽ đồ thị của hàm số 2 y = x . 2
Bảng giá trị tương ứng x và y x −4 −2 0 2 4 1 2 y = x 8 2 0 2 8 0.25 2 Đồ thị 1.2 0.25
(d ) : y = 2x +1, (d )
 : y = ax + b , (a  0) .
1.3 Tìm được a = 2 . 0.25
Tìm được b = −1 (thỏa mãn). 0.25
Bài 2. (2,0 điểm)
1. Giải phương trình và hệ phương trình sau: 2x − y = 3 a) 4 2
x − 3x − 4 = 0. b)  . 3  x + 2y =1
2. Cho phương trình 2 x − (m − ) 2 2
1 x + m − 4 = 0 , với m là tham số.
a) Tìm m để phương trình có hai nghiệm phân biệt.
b) Khi phương trình có hai nghiệm x , x , tìm tất cả các giá trị của m để biểu thức 1 2 2 2 2
P = x + x + x x + m đạt giá trị nhỏ nhất. 1 2 1 2 Bài
Tóm tắt cách giải Điểm a) 4 2
x − 3x − 4 = 0 . 2.1 0.25 Trang 2 Tìm được 2 x = −1 (loại), 2 x = 4 0.25
Tìm được x = −2, x = 2 . 2x − y = 3 4x − 2y = 6 x =1 b)      3  x + 2y =1 3  x + 2y =1 3  x + 2y =1 0.25 x =1   . 0.25 y = 1 − a) Xét pt 2 x − (m − ) 2 2
1 x + m − 4 = 0 (1) 0.25
* Ta có  = (m − )2 − ( 2 1 m − 4) = 2 − m + 5 . 5
*   0  m  . 0.25 2 5 b) 2 2
 = (m −1) − (m − 4) = 2
− m + 5  0  m  (*) 2 2.2
x + x = 2(m −1)
Theo định lí Vi-ét ta có 1 2  . 2
x .x = m − 4  0.25 1 2
P = (x + x )2 − x x + m = (m − )2 2 5 4 1 + 4  4, m   . 1 2 1 2 2
Dấu " = " xảy ra khi và chỉ khi m = 1 (thỏa mãn điều kiện (*))
Vậy P = 4 khi m = 1. 0.25 min
Bài 3. (1,5 điểm) Hai đội công nhân cùng thi công một đoạn đường nông thôn và dự định
hoàn thành công việc đó trong 16 ngày. Khi làm được 12 ngày thì đội I được điều
động đi làm việc ở nơi khác. Những ngày sau đó, đội II làm việc với năng suất gấp 1,5
lần năng suất ban đầu nên đã hoàn thành công việc đúng thời gian dự định. Hỏi theo
năng suất ban đầu, nếu mỗi đội làm một mình thì phải bao nhiêu ngày mới hoàn thành công việc trên? Bài
Tóm tắt cách giải Điểm
Gọi x , y (ngày) lần lượt là thời gian đội I, đội II làm một mình (với năng suất ban
đầu) để hoàn thành công việc, ( ĐK: x  16 , y  16 ) 0.25 1 1
Mỗi ngày đội I làm được (công việc), đội II làm được (công việc). x y
Hai đội làm chung trong 16 ngày thì hoàn thành công việc nên ta có phương trình 1 1 1 + = (1) 0.25 3 x y 16 12 12
Trong 12 ngày đầu, đội I làm được
(công việc) và đội II làm được (công x y 0.25 việc) 3 1 6
Trong 4 ngày còn lại đội II làm được 4. = (công việc). 2 y y Trang 3 12 12 6 Ta có phương trình + + =1 (2) x y y 0.25
Từ (1) và (2) ta có hệ phương trình 1 1 1 1 1 1 1 1 1 + = + = + =  x y 16  x y 16     x y 16 0.25      12 12 6 12 6 12 6  1  1  + + = + = + = 1  x y y 1  6 y 1     6 y y = 24 0.25
Giải hệ phương trình, ta được:  (TMĐK) x = 48
Vậy: Với năng suất ban đầu, đội I hoàn thành công việc trong 48 ngày,
đội II hoàn thành công việc trong 24 ngày. Bài 4. (3,5 điểm)
1. Cho tam giác ABC vuông tại A , đường cao AH .
Biết BH = 4 cm , HC = 5cm (như hình vẽ). Tính
độ dài AB và AH.
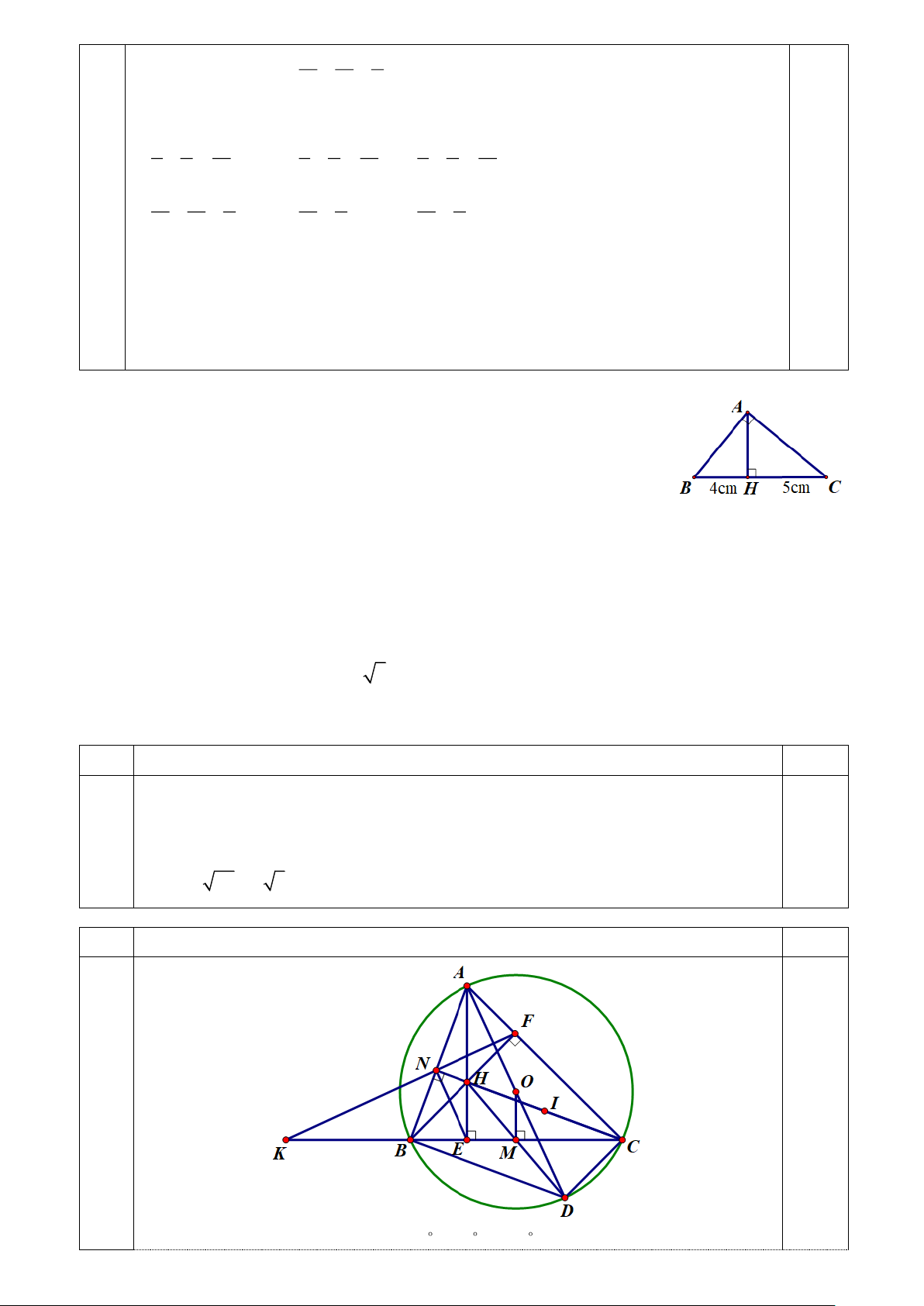
2. Cho tam giác ABC có ba góc nhọn ( AB  AC ) nội tiếp đường tròn (O; R) . Hai
đường cao AE và BF cắt nhau tại H .
a) Chứng minh tứ giác CEHF nội tiếp đường tròn. Xác định tâm của đường tròn đó.
b) Kẻ đường kính AD của đường tròn (O) . Chứng minh tứ giác BHCD là hình
bình hành. Biết BC = R 3 , tính AH theo R.
c) Gọi N là giao điểm của đường thẳng CH và AB , K là giao điểm của hai
đường thẳng BC và FN . Chứng minh BK CE = BE CK . Bài
Tóm tắt cách giải Điểm
* BC = BH + HC = 9 cm. 0.25 * 2
AB = BH.BC = 4.9 = 36  AB = 6 cm. 0.25 4.1 * 2
AH = BH.CH = 20 0.25
* AH = 20 = 2 5 cm. 0.25 Bài
Tóm tắt cách giải Điểm 4.2 0.5 a)
Chứng minh được HEC + HFC = 90 + 90 = 180 Trang 4
Suy ra tứ giác CEHF nội tiếp đường tròn đường kính HC . 0.25
Tâm đường tròn ngoại tiếp tứ giác CEHF là trung điểm I của đoạn HC . 0.25
Ta có BH // DC (cùng vuông góc với AC )
CH // DB (cùng vuông góc với AB ) 0.25
Suy ra tứ giác BHCD là hình bình hành. 4.2 0.25
Mà M là trung điểm của BC nên M là trung điểm của DH . b)
Xét tam giác AHD ta có OM là đường trung bình nên AH = 2OM 0.25 2 3R R
Tam giác OMC vuông, tính được 2 OM = R −
= . Vậy AH = R . 0.25 4 2
Chứng minh được NB là phân giác góc KNE 0.25
4.2 Suy ra NC là phân giác ngoài của góc KNE c) BK NK CK
Áp dụng tính chất phân giác ta có = = BE NE CE 0.25
Suy ra BK CE = BE CK .
Bài 5. (1,0 điểm) 1 1 1 Giải phương trình + = . 2 2 2 3x x −12x + 2024 x − 3x + 506 Bài
Tóm tắt cách giải Điểm 1 1 1 + = ĐKXĐ: x  0 2 2 2 3x x −12x + 2024 x − 3x + 506 2 2
x −12x + 2024 + 3x 1 0.25  = 2 3x ( 2 x −12x + 2024) 2 x − 3x + 506 Đặt 2 2
a = 3x , b = x −12x + 2024 (a,b  0, a  b − ) . a + b Suy ra 2 2
a + b = 4(x − 3x + 506)  x − 3x + 506 = 4.2 4 0.25 a) a + b 4 Do đó pt trở thành = ab a + b
 (a + b)2 = ab  (a − b)2 4
= 0  a − b = 0  a = b 0.25 x = −3+ 1021 2 2 2
 3x = x −12x + 2024  x + 6x −1012 = 0   (tmđk).  x = −3 − 1021 0.25 Vậy S =  3 −  102  1
Chú ý: Mọi lời giải đúng, khác với hướng dẫn chấm, đều cho điểm tối đa theo từng câu
và từng phần tương ứng. Trang 5