


Preview text:
SỞ GD&ĐT HOÀ BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10
TRƯỜNG PT DTNT THPT TỈNH NĂM HỌC 2022-2023 ĐỀ THI MÔN TOÁN ĐỀ CHÍ NH THỨC (DÀNH CHO TH Í
SINH THI LỚP CHẤT LƯỢNG CAO TOÁN)
Thời gian làm bài: 150 phút (không kể thời gian giao đề) Ngày thi: 24/6/2022
(Đề thi gồm có 01 trang, 04 câu)
Câu I (3,0 điểm)
1) Rút gọn các biểu thức:
a) A 27 2 3
b) B 6 2 5 5
2) Giải phương trình: 2x 1 x 6
3) Tìm a và b để đồ thị hàm số y ax b đi qua điểm M (1;3) và N (2; 2) .
Câu II (3,0 điểm) 2
1) Cho đường thẳng (d): y 5x 2 và parabol (P): y 2x . Tìm tọa độ giao
điểm của (d) và (P).
2) Giải phương trình: x 1 x 1
3) Hai chị em Hiền và Thảo đi mua ba lô và cặp sách chuẩn bị cho năm học
mới. Tổng giá niêm yết cho 1 chiếc ba lô và 1 chiếc cặp sách là 220000 đồng nhưng
cửa hàng đang có chương trình giảm giá 10% cho ba lô và 20% cho cặp sách nên hai
chị em phải trả tổng cộng 186000 đồng cho 1 chiếc ba lô và 1 chiếc cặp sách. Hỏi giá
niêm yết của 1 chiếc ba lô và 1 chiếc cặp sách là bao nhiêu?
Câu III (3,0 điểm).
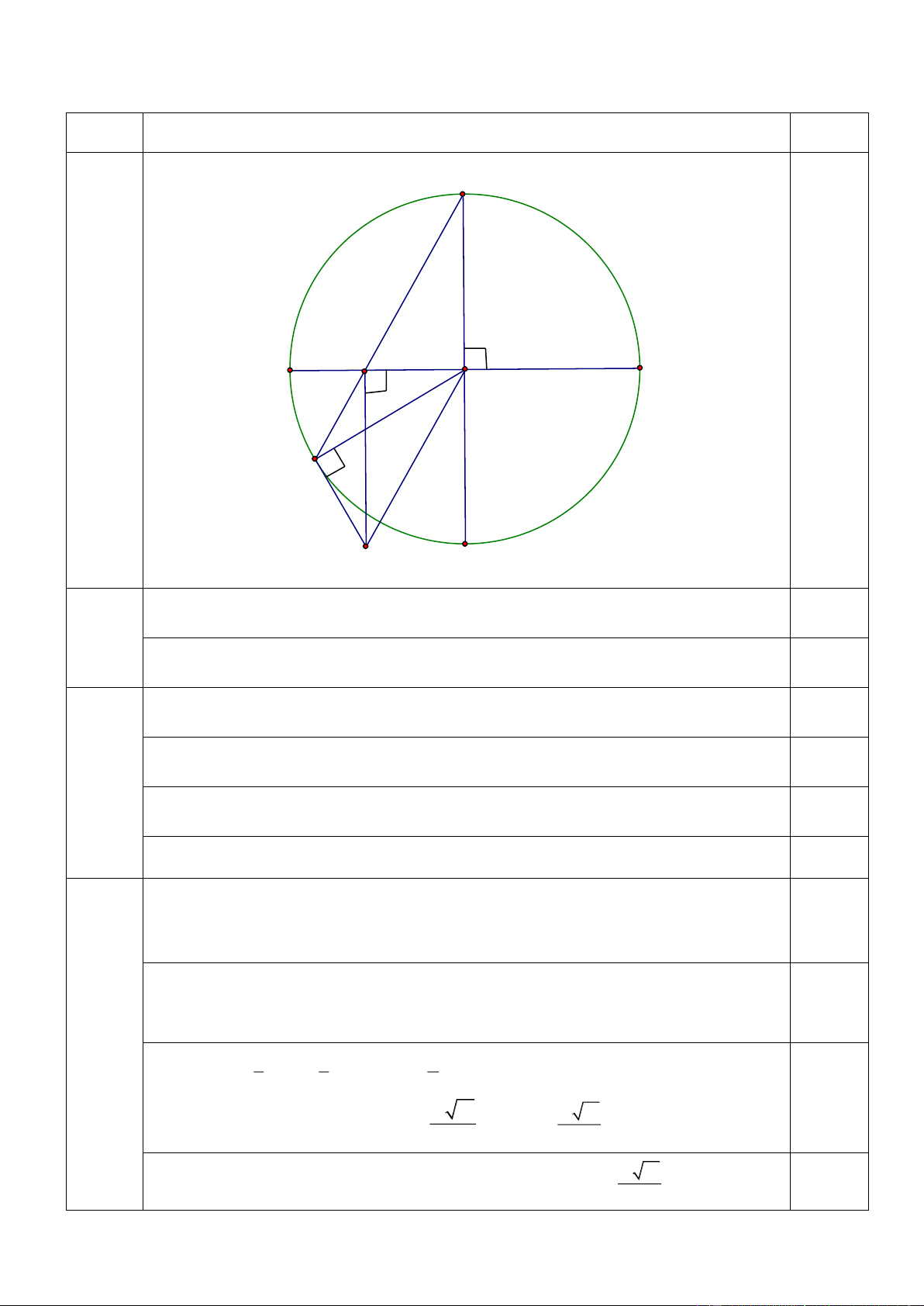
Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc với nhau. Trên
đoạn thẳng AO lấy điểm M (M khác A và O). Tia CM cắt đường tròn (O; R) tại điểm
thứ hai là N. Đường thẳng vuông góc với AB tại điểm M cắt tiếp tuyến tại N của
đường tròn (O; R) ở điểm P.
1) Chứng minh rằng: OMNP là tứ giác nội tiếp.
2) Chứng minh rằng: CN song song OP. 1 3) Khi AM
AO, tính bán kính của đường tròn ngoại tiếp tam giác OMN 3 theo R.
Câu IV (1,0 điểm).
1) Cho các số thực a, b, c thoả mãn: 2 2 2 3 3 3
a b c a b c 1 .
Tính giá trị biểu thức: 2021 2022 2023 S a b c
x y z 2) Cho các số thực ,
x y, z thỏa mãn: 6
. Chứng minh rằng z 2 .
xy yz zx 12 -------- Hết --------
Họ và tên thí sinh: ............................................. Số báo danh: ......................... Phòng thi: .......
Giám thị 1 (Họ và tên): ...................................... Giám thị 2 (Họ và tên): ................................ Trang 0 SỞ GD & ĐT HOÀ BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10
TRƯỜNG PT DTNT THPT TỈNH NĂM HỌC 2022-2023
HƯỚNG DẪN CHẤM MÔN TOÁN CLC
(Hướng dẫn chấm này gồm có 03 trang)
Câu I (2,0 điểm) Phần, Nội dung Điểm ý
A 3 3 2 3 3 0,5 1 2
B (1 5) 5 1 5 5 1 0,5 1
Nếu x thì phương trình có dạng: 2x 1 x 6 x 7 (TM ) 0,5 2 2 1 5
Nếu x thì phương trình có dạng: 2
x 1 x 6 x (TM ) 2 3 0,5 KL……. ìï a + b = 3 Vì đường thẳng ï
(d): y = ax + b đi qua điểm M (1; ) 3 , N (2;2) Þ í 0,5 3 ï 2a + b = 2 ïî
Giải hệ phương trình ta được: a = - 1; b = 4 . 0,5
Câu II(2,0 điểm) Phần, Nội dung Điểm ý
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình: x 2 2 2 0,5 2x 5x 2 2x 5x 2 0 1 . 1 x 2 1 1
Suy ra tọa độ giao điểm của (d) và (P) là: (2;8), ; . 0,5 2 2 ĐKXĐ: x ³ - 1 0,25 2
x 1 x 1 x 1 (x 1) ,(DK x 1) 0,5 2 2
x 3x 0 x 0(KTM ) . KL............ 0,25 x 3(TM )
Gọi giá niêm yết một chiếc ba lô và một chiếc cặp sách lần lượt là , x y (đồng), 0,25 * , x y
Theo bài ra ta có hệ phương trình: 3
x y 220000 x 100000 0,5 (TM ) 0
,9x 0,8y 186000 y 120000
Vậy giá niêm yết một chiếc ba lô và một chiếc cặp sách lần lượt là 100000 đồng, 120000 đồng. 0,25 Trang 1
Câu III (3,0 điểm) Phần Nội dung Điểm C M O A B N P D Có 0 OMP 90 (gt); 0
ONP 90 (tính chất tiếp tuyến) 0,5 1 Do đó OMP 0
ONP 90 OMNP là tứ giác nội tiếp 0,5
Do OMNP là tứ giác nội tiếp ONC OPM (cùng chắn OM ) 0,25
Ta có: MP // CD (cùng vuông góc với AB) OPM POD (so le trong) 0,25 2
Mà tam giác OCN cân tại O ONC OCN 0,25 OCN POD CN // OP 0,25 Do OMP 0
ONP 90 nên đường tròn ngoại tiếp tứ giác OMNP có đường 0,25
kính là OP. Nên đường tròn ngoại tiếp tam giác OMN có đường kính là OP
Ta có: CN // OP và MP // CD nên tứ giác OCMP là hình bình hành và suy ra 0,25 OP = CM 3 1 1 2
Ta có AM AO R OM
R. Áp dụng định lý Pytago trong tam giác 3 3 3 0,25
vuông OMC nên tính được MC = R 13 R 13 OP = 3 3
Vậy bán kính đường tròn ngoại tiếp tam giác OMN bằng R 13 0,25 6 Trang 2
Câu IV(1,0 điểm) Phần, Nội dung Điểm ý a, , b c 1 2 2 2 3 3 3
a b c a b c 1 2 3 2 3 2 3
a a b b c c 0 0,25 1
a 0,1 b 0, 1 c 0 1 2 2 2
a (1 a) b (1 b) c (1 c) 0 Mà 2 2 2
a (1 a) b (1 b) c (1 c) 0 a 1, b c 0 và các hoán vị của nó. 0,25 Suy ra S 1 2 2 2
x y z 6
x y z 12 0,25
xy yz zx 12
xy yz zx 12 2 2 2 2
(x y) (y z) (z x) 0
x y z 2
x y z 6 0,25 Vậy z 2
* Chú ý: Mọi cách giải khác đúng đều được xem xét và cho điểm tối đa.
-------- Hết -------- Trang 3




