Đề Tuyển Sinh 10 Môn Toán Sở GD Gia Lai 2025-2026 Có Đáp Án
Người ta cần lập hàng rào quanh khu vực bảo vệ có dạng hình chữ nhật cho một tòa nhà (hình vẽ bên). Hỏi nếu có 100 mét hàng rào bao quanh 3 mặt như trên thì diện tích tối đa của khu vực bảo vệ là bao nhiêu? Chọn ngẫu nhiên 1 học sinh lớp 9A. Tính xác suất để chọn được học sinh có điểm kiểm tra cuối kì 2 môn Toán lớn hơn 7. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 289 tài liệu
Môn: Toán 9 3.1 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TỈNH GIA LAI
TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG
NĂM HỌC 2025 – 2026 ĐỀ CHÍNH THỨC
Môn: TOÁN (không chuyên) Thời gian: 120 phút
(Không kể thời gian giao đề) x −1 x + x
Câu 1. Cho biểu thức A = + với x 0, x 1. x −1 x +1 a) Rút gọn biểu thức A
b) Tính giá trị của biểu thức A khi 3 x = 27 − 4
Câu 2. Cho phương trình 2 2x +11x + 7 = 0 .
a) Chứng minh phương trình trên có hai nghiệm phân biệt
b) Gọi x , x là hai nghiệm của phương trình trên. 1 2
Tính giá trị của biểu thức 2 T = (x + x ) + x x 1 2 1 2 Câu 3. 2x + y = 5
a) Giải hệ phương trình x − 3y = −1
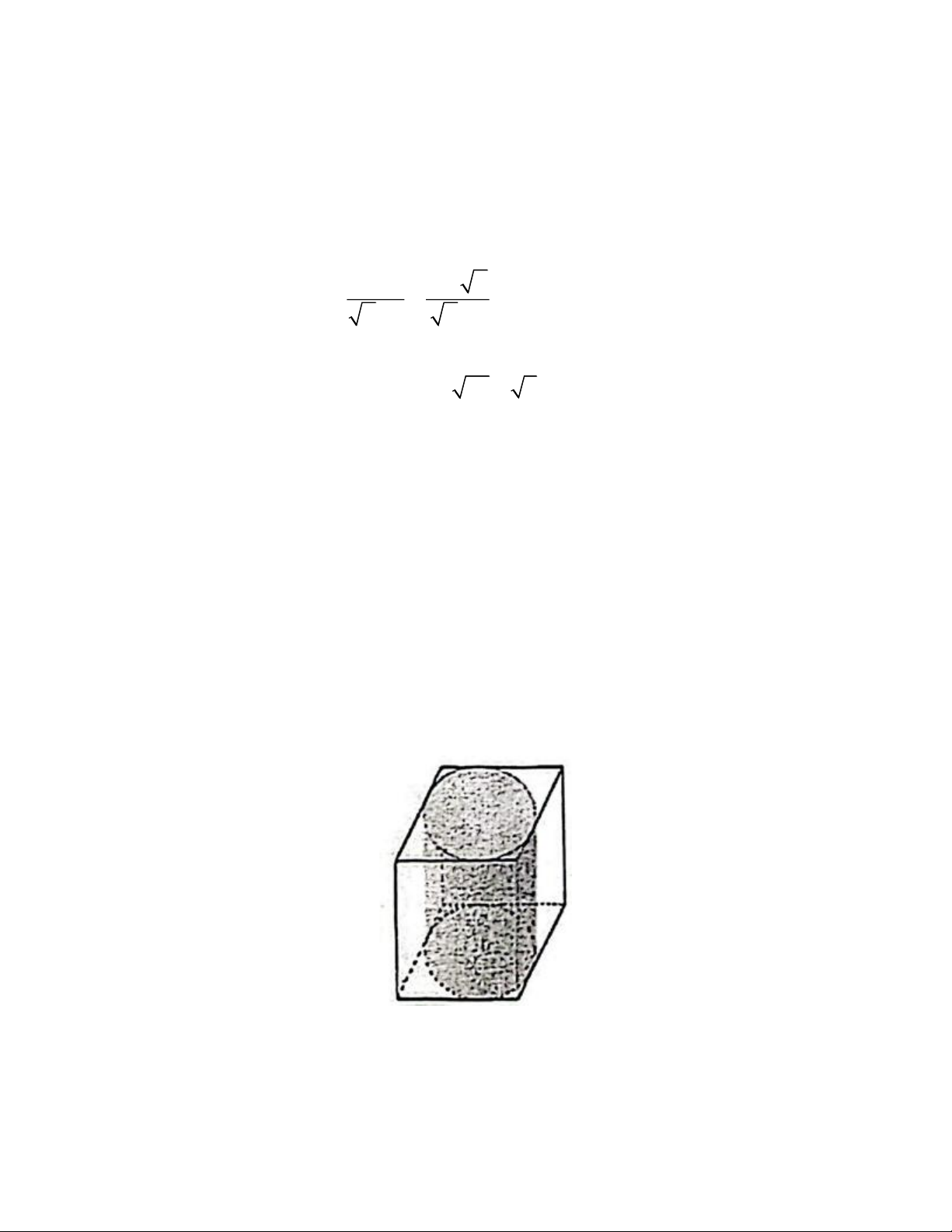
b) Một bình nước có dạng hình trụ được đặt khít vào trong một hộp giấy cứng dạng
hình hộp chữ nhật (hình vẽ bên). Biết thể tích của bình đựng nước là 3 2000cm (coi
bề dày của bình đựng nước không đáng kể). Tính thể tích của hộp giấy. sTrang 1 Câu 4.
a) Thống kê điểm kiểm tra cuối kì 2 môn Toán của 45 học sinh lớp 9A. Kết quả cho ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Số học sinh 2 2 4 m m + 2 m + 1 3 1
(với m là số tự nhiên)
Chọn ngẫu nhiên 1 học sinh lớp 9A. Tính xác suất để chọn được học sinh có điểm
kiểm tra cuối kì 2 môn Toán lớn hơn 7.
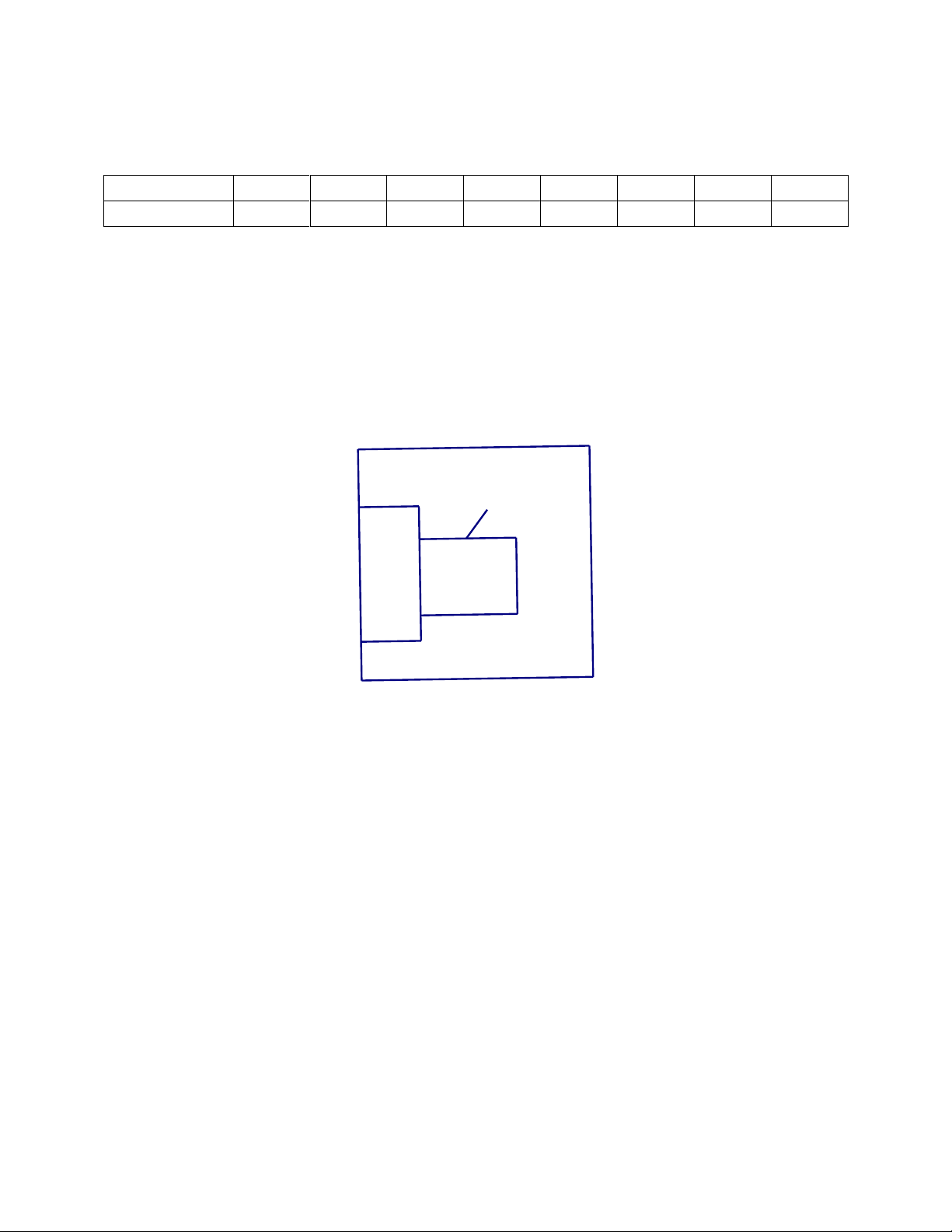
b) Người ta cần lập hàng rào quanh khu vực bảo vệ có dạng hình chữ nhật cho một
tòa nhà (hình vẽ bên). Hỏi nếu có 100 mét hàng rào bao quanh 3 mặt như trên thì
diện tích tối đa của khu vực bảo vệ là bao nhiêu? hàng rào tòa khu vực nhà bảo vệ
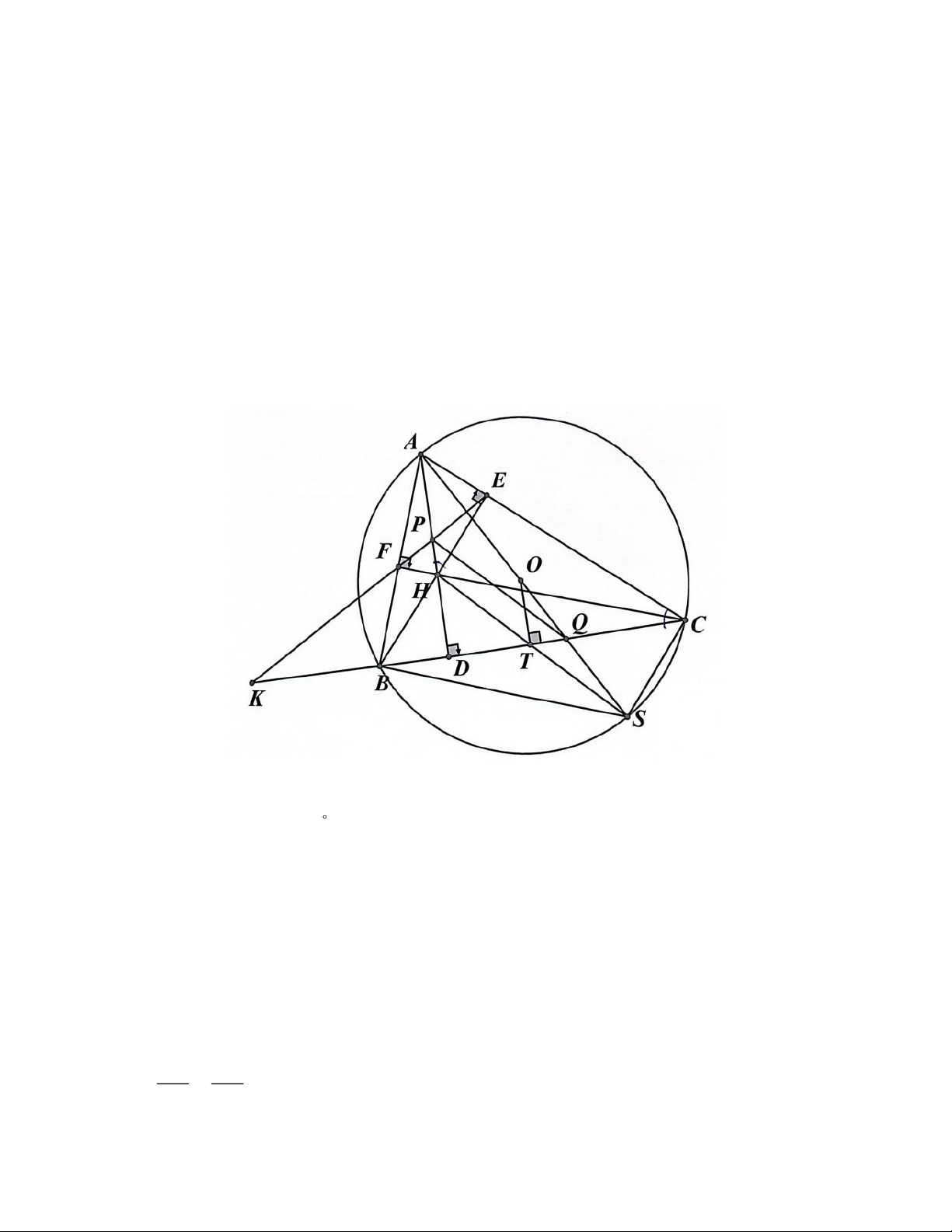
Câu 5. Cho ABC nhọn (AB < AC) nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh tứ giác BCEF nội tiếp
b) Gọi K là giao điểm của EF và CB. Chứng minh KE.KF = KB.KC
c) Gọi S là điểm đối xứng của A qua O, P là giao điểm của AH và KE, Q là giao
điểm của AS và BC. Chứng minh rằng QP song song với HS. sTrang 2 ĐÁP ÁN Câu 1. x −1 x + x a) A = + (với x 0, x 1) x −1 x +1 ( x + )1( x − )1 x( x + )1 = + A x −1 x +1 A = x +1+ x = 2 x +1 b) 3 x = 27 − 4 = 3 − 2 = 1
x = 1 không thỏa mãn ĐKXĐ nên không tính được A Câu 2. a) 2 2x +11x + 7 = 0 Ta có: 2 =11 − 4.2.7 = 65 0
Vậy phương trình luôn có hai nghiệm phân biệt. 11 − x + x = 1 2 b) Áp dụng Viet: 2 7 x x = 1 2 2 2 −11 7 135 2 T = (x + x ) + x x = + = 1 2 1 2 2 2 4 Câu 3. 2x + y = 5 a) x − 3y = −1 6x + 3y =15 x − 3y = −1 7x =14 y = 5 − 2x x = 2 y =1
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (2; 1). sTrang 3
b) Gọi r là bán kính đáy, h là chiều cao, V là thể tích hình trụ 1 Suy ra: V = 2000 1
V là thể tích hình hộp chữ nhật 2 Suy ra: 2 V = 2r.2r.h = 4r h 2 2 V r h Do đó: 1 = = 2 V 4r h 4 2 2000 Hay = V 4 2 8000 Suy ra: 3 V = (cm ) 2 8000 Vậy thể tích hộp là 3 V = (cm ) . 2 Câu 4.
Ta có tổng số học sinh là 45 Hay 12 + 3m + 3 = 45 Suy ra: m = 10
Số học sinh có điểm kiểm tra lớn hơn 7 là: 10 + 1 + 3 + 1 = 15 Nên k = 15 Tổng số học sinh n = 45
Gọi A: “Chọn học sinh lớn hơn 7” k 15 1 P(A) = = = n 45 3
b) Gọi x, y lần lượt là chiều dài, chiều rộng của khu vực bảo vệ (x, y > 0) (m)
Độ dài hàng rào bảo vệ: x + 2y = 100 (m) Suy ra: x = 100 – 2y Diện tích khu bảo vệ: sTrang 4 2 S = xy = (100 − 2y).y = 2 − y +100y 2 S = 2( − y − 50y) 2 S = 2( − y − 25) +1250 Ta có: 2 2( − y − 25) 0 y Suy ra: S 1250 y − 25 = 0 y = 25 Dấu “=” xảy ra khi suy ra x =100 − 2y x = 50
Vậy diện tích tối đa là 1250 2
m khi chiều dài, chiều rộng lần lượt là 50m, 25m. Câu 5.
a) CF, BE là hai đường cao của tam giác ABC Suy ra BFC = BEC = 90
Tam giác BFC vuông tại F nên nội tiếp đường tròn đường kính BC
Tam giác BEC vuông tại F nên nội tiếp đường tròn đường kính BC
Suy ra: BFEC nội tiếp đường tròn đường kính BC
b) Xét KBF và KEC có
EKC chung; KBF = KEC (vì BFEC nội tiếp)
Suy ra: KBF ~ KEC (g.g) KB KE Nên = KF KC sTrang 5 Suy ra: KE.KF = KB.KC (đpcm)
c) Ta có: AS là đường kính nên ABS = 90
Ta có: BAD = BCF (cùng phụ ABC ) Suy ra: BAD + HAO = HAO + OAF
Suy ra: BAQ = CAD hay PAE = BAQ Xét PAE và QAB có
PAE = BAQ,AEP = ABQ (vì FECB nội tiếp)
Suy ra: PAE ~ QAB (g.g) AP AE Suy ra: = (1) AQ AB
Ta chứng minh tương tự câu a suy ra HDCE là tứ giác nội tiếp Nên AHE = ACB Mà ACB = ASB Suy ra AHE = ASB Xét AHE và ASB có AHE = ASB,AEH = ABS = 90
Suy ra: AHE ~ ASB (g-g) AE AH Suy ra: = (2) AB AS AQ AS Từ (1), (2) suy ra = AP AH
Suy ra: PQ // HS (Thales đảo) sTrang 6